含电动汽车的新能源小镇源荷协调优化

罗晓乐，宋 洋，徐 翔，梁 家，车靖峰

（国网吉林省电力公司松原供电公司，吉林 松原 138000）

在新能源小镇中接入电动汽车能够为可再生能源的消纳问题提供新的解决途径，但同时也会给新能源小镇的规划、经济运行及综合调度带来困难。因此，研究电动汽车参与新能源小镇的优化运行可以为解决此类问题提供理论支撑和实际指导价值。

在提高新能源小镇的能源利用率及模型建立方面，文献［1］提出4 种计及热网热能传输动态特性的电-热综合能源系统日前优化调度方案，通过最优分配能源设备出力，使总运行成本最低并加入弃风惩罚作为目标函数，分析不同优化调度方案通过改变各能源设备出力带来的风电消纳率与经济性的结果。

在考虑含电动汽车的新能源小镇优化运行方法方面，文献［2］不仅考虑了新能源小镇的出力特性，而且计及了电动汽车充电对经济运行的影响，通过一种改进后的粒子群优化算法对模型寻优求解，大大增加了系统的经济效益；文献［3］重点考虑了电动汽车接入新能源小镇后，电动汽车的充电负荷对风力发电系统可靠性的影响，采用虚拟联合负荷的概念统一考虑含风电电力系统的波动性因素，借助V2G 技术，提出了一种用以平缓虚拟负荷波动性进而提高系统可靠性的电动汽车充电控制策略优化模型，并用增加递减惯性权重因子的粒子群算法求解该模型，得出了具体的电动汽车充电策略；文献［4］分析了新能源小镇的网络架构与能量互动特点，阐明了电动汽车的跨时空能量搬移特性，研究了电动汽车与小镇、电动汽车用户与运营商之间的能量互动关系，提出了新能源小镇的智能经济调度策略，以及新能源小镇经济调度分别与容量配置和电动汽车充电电价的协同优化方法；文献［5］主要围绕大规模电动汽车的充放电行为和计及电动汽车的新能源小镇的调度运行展开分析，总结了电动汽车对新能源小镇的影响，探讨了电动汽车充电行为及并入系统的重要性。

1 含电动汽车的新能源小镇模型

在某新能源小镇全天负荷预测值已知的前提下，基于新型电力系统整体框架，提出以运行成本最小为目标函数，同时考虑电力系统、热系统以及能量转换单元安全运行的约束条件，建立含电动汽车的新能源小镇优化模型。

1.1 目标函数

在新能源小镇运行系统中加入热电联产、热泵、电锅炉、电动汽车等各类设备的约束条件，建立系统模型，以该小镇的数据作为算例的数据来源，对不同补偿电价的情况进行仿真分析。新能源小镇运行总成本最小的目标函数为

式中，T为24 h 时段；Th为电价高峰时段；Cf为燃料成本；CW为弃风惩罚成本；Cb为电动汽车补偿成本；λf为CHP单位耗煤成本；λW为单位弃风成本；λb为单位补偿电价；fCHP为热电机组耗煤量；PCHP为热电机组电出力；QCHP为热电机组热出力；a、b、c、d、e、f 均为热电机组耗量特性参数；PW为风电机组出力；PW,fore为风电机组预测出力；ΔPEV,out(t)为电动汽车负荷转出量；PCHP为热电机组电出力；QCHP为热电机组热出力。

该小镇采用激励型补偿引导充电负荷有序转移，协助风电并网消纳。电动汽车用户根据所提供的补偿电价，将用电高峰时段部分充电负荷转移至用电低谷时段，从而在消纳夜间富余风电的同时减少电力系统在电价高峰时段的发电量，缓解系统调峰压力。其中，补偿电价ΔDp(t)与充电负荷转移量ΔPEV(t)的关系为

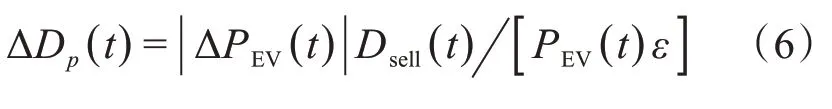
式中，ε为补偿电价弹性系数；Dsell(t)为t时段系统售电电价。

电动汽车的日行驶里程近似服从对数正态分布，概率模型为

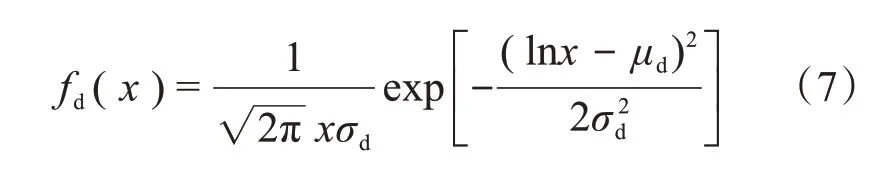
式中，x为电动汽车行驶里程；μd为期望值为方差，且μd=3.2，σd=0.88。

电动汽车的电池和行驶里程满足如下关系：

式中，E为电动汽车电池的起始值；R为电池充满之后电动汽车行驶的里程。因此，关于E的概率密度函数为

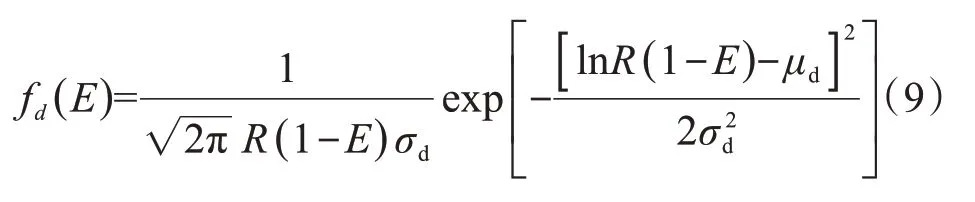
如果定义电动汽车返回时刻为充电开始时刻，其充电时刻服从正态分布，概率密度模型为

式中，μT=17.6，σT=3.4。

对于N台电动汽车，起始充电时刻为T，每次电量都充满。当t≥T时，电动汽车的有功需求的期望值为

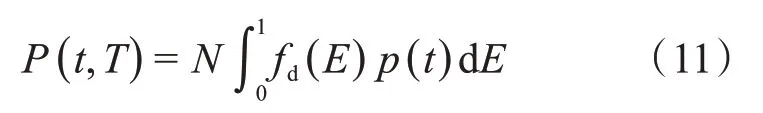
p(t)为电动汽车t时刻的有功充电功率：

式中，tEV为电池在当前时刻下充电至满电量的时长；Pcr表示充电速率；由中心极限定理可知，充电负荷PEV在t时刻服从正态分布；μEV,t为电动汽车在t时刻充电负荷量的期望值；σEV,t为标准差。

充电量的概率密度函数为

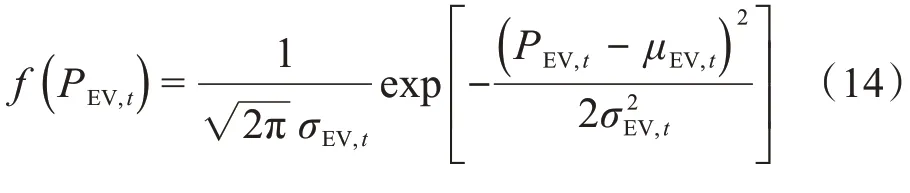
1.2 约束条件

1.2.1 系统约束

1）电功率平衡约束

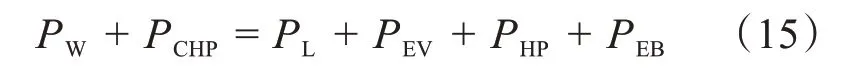
式中，PW为风电出力；PCHP为热电联产机组电出力；PL为用户的常规电负荷；PEV为电动汽车的充电功率；PHP为热泵耗电功率；PEB为电锅炉的耗电功率。

2）热功率平衡约束

式中，QCHP为热电联产机组热出力；QHP为热泵机组热出力；QEB为电锅炉热出力；QL为用户热需求。

1.2.2 设备约束

1）风电机组约束

2）电锅炉约束

式中，PEB为输入电锅炉的电功率；ηEB为电锅炉电制热的效率系数；QEB为电锅炉的输出热功率；QEBmax为电锅炉热出力的上限。

3）热泵约束

式中，PHP为输入热泵的电功率；ηHP为热泵电制热的效率系数；QHP为热泵的输出热功率；QHPmax为热泵热出力上限。

4）电动汽车充电负荷调节前后平衡约束

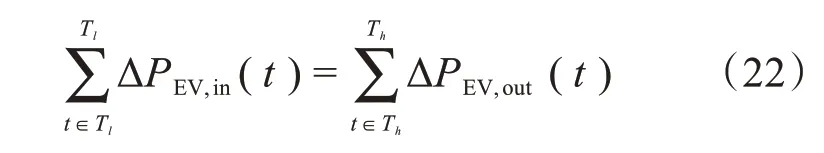
式中，Tl为电价低谷时段；Th为电价高峰时段；ΔPEV,in(t)为电价由高峰转入的电动汽车充电负荷；ΔPEV,out(t)为电价由高峰转出的电动汽车充电负荷。

5）CHP机组约束

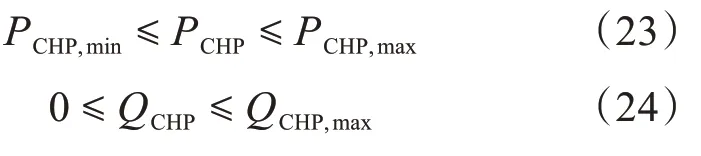
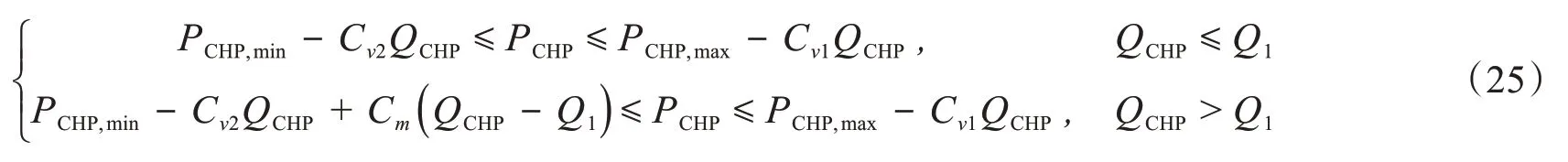
式中，PCHP,min和PCHP,max分别为CHP 热功率的下限和上限；QCHP,max为CHP 热出力的上限；Cv1、Cv2、Cm均为CHP 的热电耦合参数，表示CHP 电功率和热功率的热电耦合关系；Q1为热电机组在最小凝汽工况下运行且进汽量最小时的热出力值。

1.3 求解方法

本文建立的含电动汽车的新型电力系统源荷协调优化模型是一个多变量、非线性和多约束的求解最小值问题。fmincon函数可以用于求解非线性多元函数的最小值。非线性优化模型描述如下：

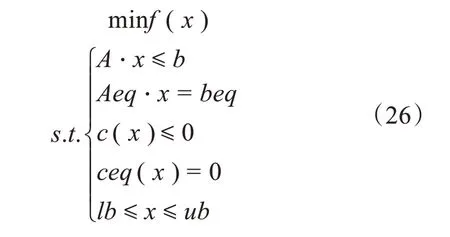
式中，A和b分别为线性不等式约束；Aeq和beq分别定义线性等式约束；c(x)为非线性不等式约束；ceq(x)为非线性等式约束；lb和ub分别为变量的下限和上限。

2 算例仿真

2.1 算例来源

以某新能源小镇为研究对象，小镇内的能源来自于120 MW 的风电场和330 MW 热电厂，镇内负荷以某冬季典型日电负荷和热负荷为例，能源转换设备包括热电联产机组（1 台20 MW）、热泵（COP系数为3）、电锅炉（1 台20MW，效率为0.9）、电动汽车（10 000辆，特斯拉Model 3标准续航后驱升级版，电池容量为55 kW·h，慢充功率为7 kW，快充功率为250 kW）。7:00～21:00为小镇用电峰时段，电价为0.52 元/(kW·h)；21:00～7:00 为小镇用电水平谷时段，电价为0.4元/(kW·h)。

2.2 仿真分析

待算例数据参数总结归纳后，将电动汽车调度前的数据写入MATLAB 算例仿真程序中，针对3 种不同场景的补偿电价仿真结果，从负荷波动率、弃风率、系统运行成本等方面进行对比分析：

场景1：只考虑对源侧进行协调（电价补偿为0，即电动汽车为无序充电状态）；

场景2：考虑源荷双侧互动（电价补偿为0.1）；

场景3：考虑源荷双侧互动（电价补偿为0.2）。

电动汽车在场景1 中的充电负荷如图1 所示。在1:00～7:00时，充电负荷几乎为0，说明在此时间段内，如果不对系统进行调节，那么居民们几乎不会为电动汽车充电；在7:00～13:00和15:00～21:00时，居民会大规模对电动汽车充电。而居民的基本用电负荷时间为7:00～21:00 时，当常规高峰用电负荷叠加大规模电动汽车充电负荷时，系统的总用电负荷会发生剧烈的波动，其峰谷差也会大幅度变化。

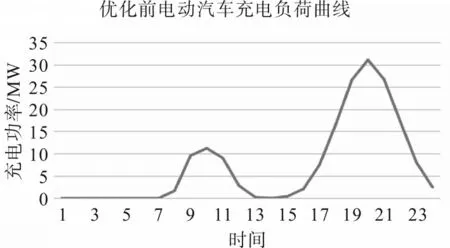
图1 场景1电动汽车充电负荷

电动汽车在场景2和场景3中的充电负荷曲线如图2和图3所示。电动汽车大规模充电时间由调节前的峰荷时间转变为常规电负荷的谷荷时间，充电时间为1:00～7:00 和21:00～24:00 时。常规电负荷搭配此种充电行为可有效地缩小峰谷差，减轻系统压力。

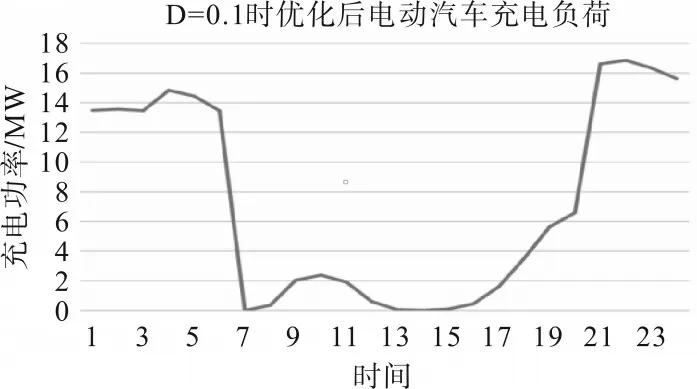
图2 场景2电动汽车充电负荷

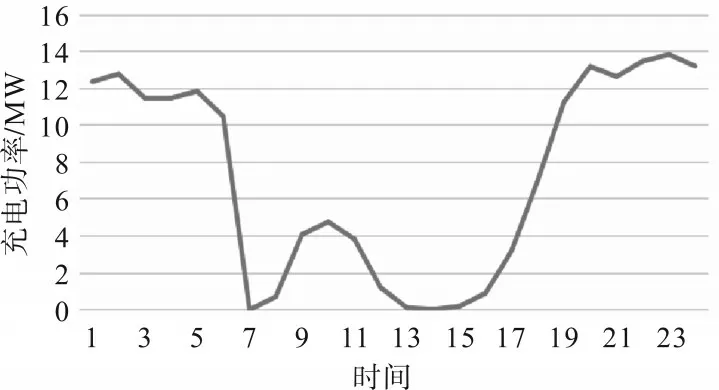
图3 场景3电动汽车充电负荷

场景1 和场景2 总电负荷对比结果如图4 所示。场景2 的总电负荷曲线比场景1 更加平缓，在一定程度上“削峰填谷”，并减小了系统峰谷差。

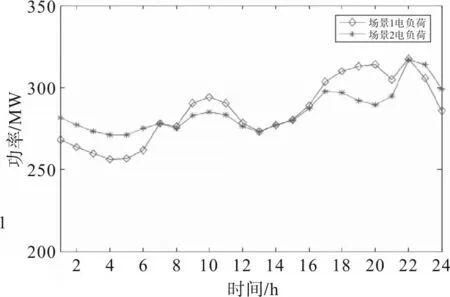
图4 场景1和场景2总电负荷曲线

将3 种场景的仿真结果进行对比，如图5 和表1所示。

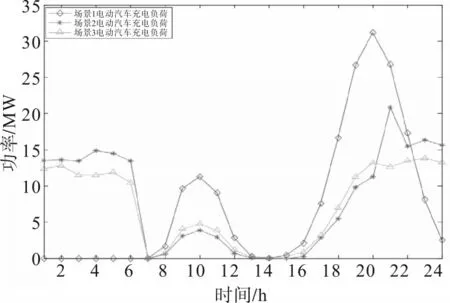
图5 3种场景下充电负荷对比

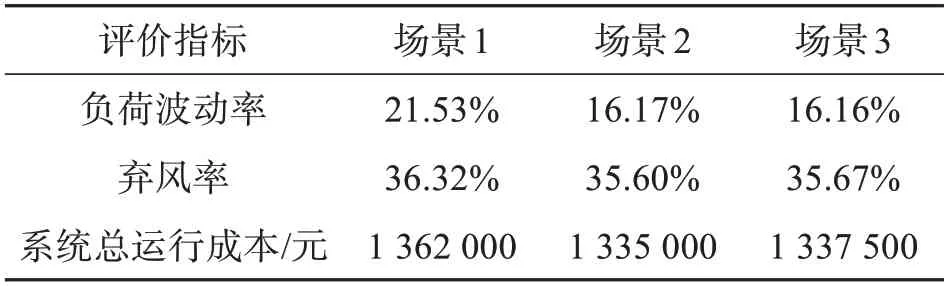
表1 3种场景仿真结果对比

根据表1 可得出不同补偿电价下的负荷波动率，如图6所示。

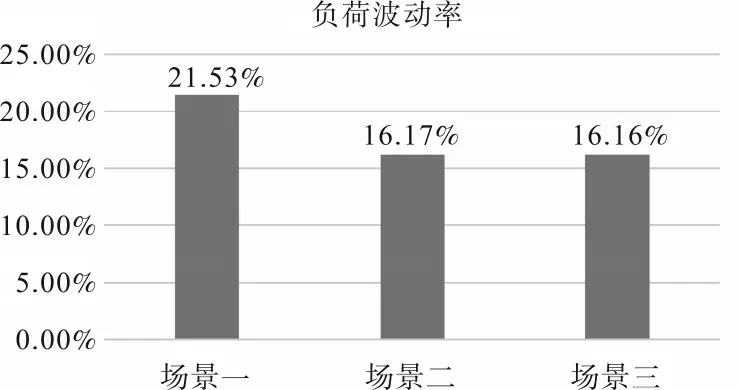
图6 不同场景下的负荷波动率

当在场景1 时，电动汽车纳入新型电力系统后，电动汽车的充电负荷对系统负荷影响较大，负荷波动率为21.53%，是3 种补偿电价中最高的情况，而场景2和场景3的负荷波动率几乎一致，明显低于场景1。当补偿电价高于0.1 之后，负荷波动率的降低效果不再明显。

3 种场景对弃风的影响如图7 所示，运行成本如图8所示。

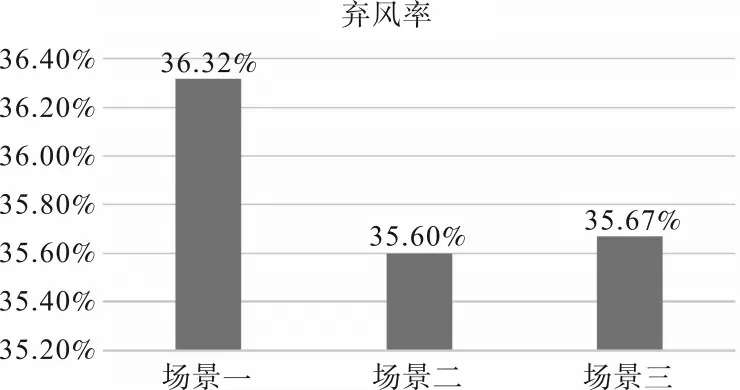
图7 3中场景的弃风率

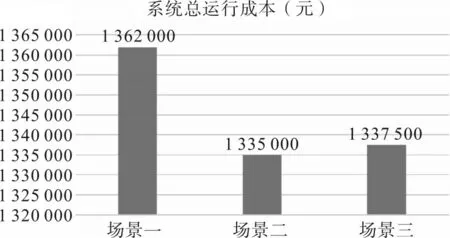
图8 3种场景的运行成本

场景2 和场景3 的弃风率比场景1 低，由于电动汽车充电曲线的调整，可以为系统预留更多的风电并网空间，促进风电消纳。场景2 和场景3 的运行成本比场景1 少，但场景3 比场景2 略高，这是由于电动汽车的充电调度使得系统在峰时段的负荷减少，而在谷时段的负荷增多，从而节省了成本。但由于电动汽车数量较少，当补偿电价再次增加的时候，所带来的运行成本会随之增加。

3种场景的各项指标对比分析如图9所示。

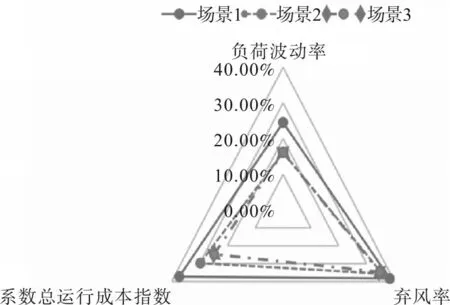
图9 3种场景的负荷波动率、弃风率和系统运行成本的对比结果

将3 类指标进行对比后可知，场景2 和场景3的总体情况几乎一致，但场景2 的经济性最好，且弃风率和负荷波动率也较小，虽与场景3 略有差别，但两者的数据相差极小。因此，可认为场景2是最佳方案，各项指标远远好于场景1的情况。

3 结论

本文以某小镇为例建立了含电动汽车的新能源小镇优化运行模型，通过算例针对不同场景下电动汽车接入新能源小镇运行而产生的不同影响进行了分析，仿真结果表明：

1）在未对电动汽车充电负荷进行调节的模型中，用户因生活用电习惯大多在常规用电峰荷时对电动汽车进行充电。而这一习惯导致系统总负荷在谷荷时用电水平较低，而在峰荷时段由于电动汽车的大规模接入使得其和原本的常规用电峰荷叠加，导致系统的总用电负荷在7:00～21:00 高峰用电时段急剧升高。因此，系统在优化前的峰谷差较大，总用电负荷波动剧烈，且弃风水平较高，总成本增加。当对系统进行调节，将高峰时期的部分充电负荷转移至低谷期时，系统的总用电负荷曲线波动程度明显降低，峰谷差缩小，弃风量减小。

2）当对园区的负荷进行优化时，可优先采用清洁能源发电，降低对传统火电机组的依赖性，有效消纳了园区的风电。因此，对模型优化后，传统能源和清洁能源的交替配合利用能够满足用户的供电和供暖需求，且大幅度提高了清洁能源利用率。由于清洁能源的合理使用，系统的总运行成本明显降低。