中国城市群高新技术企业全要素生产率的空间差异与动态演进
2022-02-14孙红军赵祚翔
孙红军,赵祚翔
(1.中国标准化研究院 国家标准馆,北京 100191;2.中国科学院 科技战略咨询研究院,北京 100190)
一、引言
目前,高新技术企业(以下简称高企)已经成为落实创新驱动发展战略和提高全要素生产率的核心抓手(罗利华等,2021;方文中和罗守贵,2016)。然而,作为典型的大国经济体,我国各地高企全要素生产率水平差异较大,尤其是不同城市群高企全要素生产率增长不平衡不充分的问题表现很突出。同时,当前围绕不同城市群高企全要素生产率的研究相对缺乏,以往研究较少从19 个城市群高企视角展开全要素生产率空间差异与动态演进分析。鉴于此,本文聚焦问题是:我国19 个城市群全要素生产率水平如何?是否存在明显的空间差异?其区域内、区域间差异大小及其贡献率如何?呈现出何种时空演进特征和分布规律?应采取哪些举措促进促进不同城市群高企协调发展?全面、准确回答这些问题对于促进区域协调协同发展具有重大的理论和现实意义。
本文将从以下4 个方面对现有相关研究展开文献述评:
第一,就全要素生产率研究对象而言,现有研究较多聚焦于国家、省市视角开展全要素生产率测算与分析。例如,杨雪梅等(2022)测算了中国、日本、美国和德国在1995—2017 年的全要素生产率。郭雪萌等(2022)测度了我国及主要创新型国家2001—2018 年的全要素生产率。王琴梅和罗瑞(2022)则关注了2003—2019 年中国城市全要素生产率。少有文献关注城市群高企层面全要素生产率研究,尤其是缺乏从19 个城市群视角展开分析的研究(李文静,2021;段文斌和尹向飞,2009)。鉴于此,本文从19 个城市群作为区域切入视角,探究19 个城市群高企全要素生产率区域差异问题。
第二,就全要素生产率测算方法而言,测算全要素生产率的方法主要有参数法和非参数方法(程郁和陈雪,2013)。由于非参数法(Malmquist 生产率指数)无需设定函数形式,简单易行,受到了众多学者青睐。例如,申晨等(2022)运用非期望产出的两阶段超效率(super-SBM)网络数据包络(DEA)模型及结合全局机器学习生产率指数测算了中国2005—2017 年30 个省市工业绿色全要素生产率、生产效率和治污效率。张优智和乔宇鹤(2022)利用DEA-Malmquist 方法测度2009—2017 年我国30 个省份的制造业绿色全要素生产率。但是非参数方法对数据模型算法要求较高,同时并未考虑随机因素对模型的影响,进而影响测算结果的科学性和准确性。参数方法(如超越对数随机前沿生产函数)能有效解决上述问题,并能通过对模型适用性进行检验,使得模型能较好模拟实际经济情况(孙红军和王胜光,2020;孙红军等,2020)。鉴于此,本文后续将采用超越对数随机前沿生产函数来测算全要素生产率。
第三,就全要素生产率空间差异测算而言,大多研究在测度全要素生产率空间差异水平,普遍采用传统基尼系数、变异系数、Theil 指数等方法(孙红军等,2020;杨明海等2017,2018;陈明华等,2018)。其中,传统基尼系数与变异系数无法准确实现对空间差异进行区域内、区域间差异分解;而Theil 指数能有效将空间差异分解为区域内和区域间差异。王兆峰等(2022)运用Theil 指数对长株潭城市群区域内差异和区域间差异进行了分解,结果发现区域内差异是整体差异的主要贡献者。鉴于此,本文将采用Theil 指数对19 个城市群高企全要素生产率的空间差异进行测度和分解。
第四,现有文献主要运用直接对比方法来探究全要素生产率随时间的变动趋势,其做法就是将不同区域全要素生产率随时间增长的态势进行直观对比分析,进而对其演进过程进行定性研判(杨清可和段学军,2014;段敏芳和吴俊成,2017)。但这种方法无法定量准确刻画不同城市群高企全要素生产率空间不平衡的时空演进规律,更无法揭示空间关联效应下的不同城市群高企全要素生产率的转移特征。鉴于此,本文将采用Kernel 核密度估计和空间Markov 链估计方法来解决上述问题。
通过上述分析,本文将采用超越对数随机前沿生产函数来测算2015—2019 年19 个城市群高企全要素生产率,然后运用Theil 指数测度和分解19 个城市群高企全要素生产率的整体区域差异、区域内及区域间差异,研判区域差异的来源。在此基础上,再采用Kernel 核密度估计和空间Markov 链估计方法来揭示19 个城市群高企全要素生产率的时空动态演进特征和规律。最后,围绕上述研究结论提出促进19 个城市群高企协同发展的对策建议。
二、方法与数据
(一)超越对数随机前沿分析方法
本文设定的超越对数形式的随机前沿分析模型如式(1)所示:
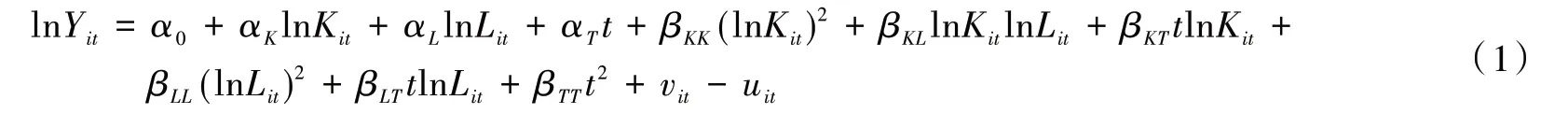
其中:Yit为i城市高企在t年的实际生产产出,本文参照方文中和罗守贵(2016)的做法,采用高企营业收入衡量生产产出;Lit为i城市高企在t年的劳动要素投入,本文采用高企年末从业人员数量衡量劳动投入;Kit为i城市在t年的资本要素投入,本文采用高企年末资产合计(火炬统计有标准口径的年末资产合计指标避免了资本存量统计口径不一致与不同折算方法所带来的误差)衡量资本投入;t为技术进步的时间演变项;所有的α、β均为待估参数;α0为待估常数;αK为资本要素的待估系数;αL为劳动要素的待估系数;αT为时间t的待估系数;βKK为资本要素二次项的待估系数;βLL为劳动要素二次项的待估系数;βTT为时间t二次项的待估系数;βKL为资本要素和劳动要素交叉项的待估系数;βKT为资本要素和时间交叉项的待估系数;βLT为劳动要素和时间交叉项的待估系数;vit为随机误差项;uit为技术无效率项。由此可见,超越对数生产函数较一般Cobb-Douglas生产函数增加了二次项和交叉项。
参照Kumbhakar 和Lovell(2000)的研究,将全要素生产率增长率进行分解,如式(2)所示:

其中:TFPit为i城市在t年的全要素生产率增长率;TCit为i城市在t年的技术进步率;TECit为i城市在t年的技术效率变化率;SECit为i城市在t年要素规模效率变化率。式(2)表明,可将全要素生产率增长率进一步分解为技术进步率、技术效率和规模效率变化率。接下来,本文将依次分析技术进步率、技术效率变化率、规模效率变化率的具体测算过程。
技术进步率。再次回归超越对数的随机前沿分析的本质,可以发现,这种分析方法实质是以时间(t)演变来表征技术进步的变化。基于此,本文以产出随时间的变化而变化来表征技术进步,反映在生产函数的数理关系上就是将式(1)的产出Yit对时间t求偏导,据此,得到式(3):
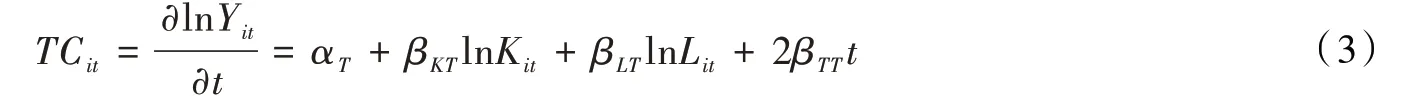
技术效率变化率。技术效率可以用该生产者实际产出的期望与随机前沿产出的期望的比值来进行计算。本质而言,技术效率反映的生产者实际产出逼近前沿产出的程度,而技术无效率反映的生产者实际产出偏离前沿产出的程度,两者反映的是完全相反的生产活动。因此,可以通过求出技术无效率来间接求出技术效率变化率,本文将利用技术无效率项uit对时间t求偏导的相反数来测算技术效率变化率,如式(4)所示,假设ui的分布服从非负断尾正态分布,即ui~N+(μ,),η为待估参数,当η>0 时,技术无效率项uit随着时间增加而减小,即技术效率增加;当η<0 时,技术无效率项uit随着时间增加而变大,即技术效率降低;当η=0时,模型则退化为截断正态分布下的形式,此时技术无效率项不再随着时间变化。
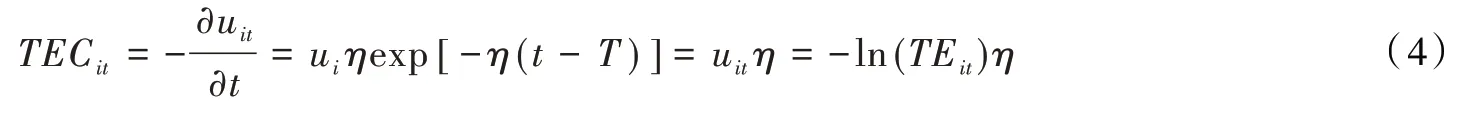
其中:TE为技术效率。
要素规模效率变化率。要素规模效率反映单位投入要素带来的额外产出。由于本文采用以资本和劳动作为要素投入。因此还可将要素规模效率进一步分解为资本要素规模效率变化(SECKit)和劳动要素规模效率变化(SECLit),即有如下关系:
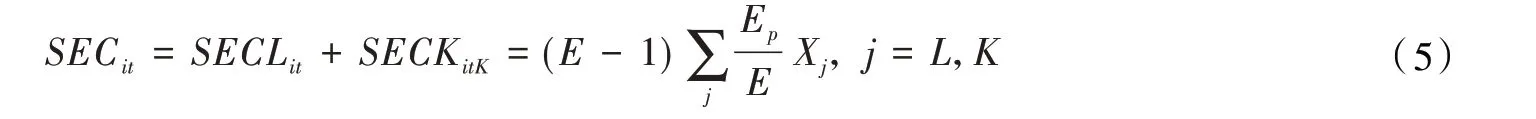
其中:E为资本和劳动投入要素规模弹性的加总;Ep为p种投入要素的规模弹性;Xj为第j种投入要素的增长率。因此,本文就将要素规模效率变化率的求解问题转化为各投入要素规模弹性的计算问题。劳动与资本投入要素规模弹性的计算过程如式(6)、式(7)所示。

(二)Theil 指数方法
本文将采用Theil 指数方法来测算和分解全要素生产率增长的区域差异,Theil 指数定义如式(8)所示。
为探究各城市群高企全要素生产率的区域差异,本文选择Theil 指数来衡量19 个城市群高企全要素生产率的区域差异,并将空间非均衡性分解为区域内差异与区域间差异。区域内和区域间差异分解及贡献率如式(9)~式(11)所示。

其中:TH为总体Theil 指数,其衡量19 个城市群高企总体区域差异;TFPi为i城市群高企全要素生产率,THw和THb分别为区域内和区域间的Theil 指数,分别衡量各个城市群高企全要素生产率的区域内差异,不同城市群高企之间全要素生产率的区域间差异;μ为n个城市群高企全要素生产率的平均值;μz为第z个城市群高企全要素生产率的平均值;THz为z城市群高企的Theil 指数;fz为第z个城市群高企所含样本数占总样本数的比重。Theil指数的取值一般介于0~1 之间,该指数越趋近于0,则表示各个样本之间的差异越小,均等化程度越高,反之亦然。
(三)Kernel 密度估计非参数方法
本文将采用Kernel 密度估计非参数方法来探究19 个城市群高企全要素生产率的空间不平衡的分布动态演进特征。Kernel 密度估计是通过对比不同时间节点的样本分布的异同点来考察样本分布动态演进趋势,已成为研究空间不平衡的常用方法。本文假设随机变量x的密度函数为f(x),点x处的概率密度则由式(12)表示。

其中:N为观测值的个数;h为带宽;K(·)为Kernel 函数;Xi为观测值。Kernel 密度函数拥有均匀核、四次核、高斯核等多种表达形式,其中高斯核最为常用。因此,本文也采用高斯核对19 个城市群高企全要素生产率的分布动态演进过程进行估计。高斯核函数表达式如式(13)所示。

(四)空间Markov 链估计方法
空间Markov 链估计方法将空间滞后或空间关联因素考虑到转移概率矩阵中(Anselin et al,2008),以此来揭示空间关联效应下,周边城市群高企全要素生产率水平对本城市群高企全要素生产率转移演变特征的影响水平。具体而言,根据各城市是否相邻设定空间邻接权重矩阵,然后将传统Markov 链估计中的N×N转移概率矩阵分解为N×N×N转移概率矩阵,即考虑了N层空间关联环境下,不同水平城市群高企转移趋势。最后,求出t时期某城市群高企在不同空间滞后类型的条件下,由t-1 时期A 状态转移到t时期B状态的空间概率Pij(N),以此刻画空间关联与全要素生产率转移特征之间的关系。
(五)研究对象与数据来源
根据《中华人民共和国国民经济和社会发展第十四个五年规划和2035 年远景目标纲要》,本文以京津冀、长三角、珠三角、成渝、长江中游、山东半岛、粤闽浙沿海、中原、关中平原、北部湾、哈长、辽中南、山西中部、黔中、滇中、呼包鄂榆、兰州-西宁、宁夏沿黄、天山北坡19 个城市群高企为研究对象。本文数据来源于科技部火炬中心面向全国高企开展的年度调查统计。同时考虑到数据可获性和准确性,参照已有研究(牛冲槐等,2014;夏文飞等,2020)的做法,按照高企注册地将高企上报指标进行加总,最终构建2014—2019 年209 家地级市高企层面的面板数据。
三、19 个城市群高企全要素生产率的区域差异
(一)生产函数模型的选择
本文在采用随机前沿方法测算全要素生产率增长率之前,还需要对超越对数生产函数的随机前沿模型适用性进行检验,即对生产函数的具体形式进行判定,本文采用的判定方法有方差参数检验和假设检验等两种方法。采用Battese 和Coelli(1992,1995)设定的方差参数方法进行检验,具体检验公式为

其中:σu为技术无效率项;σv为随机误差项;γ为技术无效率项占复合扰动项的比例。具体而言,若原假设γ=0 被接受,则表明实际产出与前沿产出之间偏差全部来源于随机误差项,则采用最小二乘法回归即可,否则采用随机前沿进行估计。
设定4 个假设检验,以便确定非中性技术进步的超越对数随机前沿函数模型是否合理。第一,H0:η=0,即假设技术无效率不随时间变动的生产函数是合适的(模型1.1);第二,H0:αT=βKK=βKL=βKT=βLL=βLT=βTT=0,即采用不含技术进步(t)的C-D 生产函数是合适的(模型1.2);第三,H0:βKK=βKL=βKT=βLL=βLT=βTT=0,即采用含技术进步(t)的C-D 生产函数是合适的(模型1.3);第四,H0:αT=βKT=βLT=βTT=0,即采用不含技术进步(t)的生产函数是合适的(模型1.4)。上述4 种情况分别通过广义似然统计量λ来进行检验,具体检验公式为

其中:L(H0)和L(H1)分别是零假设和备择假设前沿模型的似然函数值。如果零假设成立,那么检验统计量λ服从混合卡方分布,自由度为受约束变量的数目。将超越对数的随机前沿函数设定为基准模型[备择假设H1,如式(15)所示]。
表1 给出了随机前沿分析回归结果,模型1 为本文定义的基准模型,即超越对数函数的随机前沿模型,模型1.1 是技术无效率不随时间变动的生产函数,模型1.2 是不含技术进步(t)的传统的C-D 生产函数,模型1.3是含技术进步(t)的C-D 生产函数,模型1.4 是不含技术进步(t)的生产函数,这4 种生产函数对应上述4 种假设。根据方差参数检验方法,在各个随机前沿模型中,γ值都大于0.52,说明总误差中的52%以上是由于存在技术无效率而造成的,即采用随机前沿分析较传统普通最小二乘法(OLS)回归更能有效解释城市群高企生产活动中技术效率及其变化。根据广义似然统计量λ来进行检验,表2 给出了相关假设检验结果,结果发现,模型1.1、模型1.2、模型1.3、模型1.4 的原假设均被拒绝,说明采用原基准模型1 即超越对数生产函数的随机前沿分析模型是合理的。此外,η值显著为正,说明技术效率的时间趋势较为明显。综上所述,采用超越对数生产函数形式的随机前沿分析模型来测算城市群高企全要素生产率增长率是合适的。

表1 随机前沿回归结果

表2 假设检验回归结果
(二)19 个城市群高企整体全要素生产率的表现
一方面,为了进一步全面反映19 个城市群高企全要素生产率的长期演变态势;另一方面,也为后续采用Theil 指数方法对城市群高企全要素生产率的区域差异进行区域内和区域间分解,本文参照已有研究(陈明华等,2018;王兵等,2010)的做法,以2014 年为基期(以2014 年为1),对全要素生产率增长率进行累计处理,从而获得2015—2019 年累计全要素生产率指数(下文如无特别说明,全要素生产率均指累计全要素生产率指数)。本文根据测算结果绘制了19个城市群高企整体累计全要素生产率增长指数的折线图,如图1 所示。图1 显示,整体高企累计全要素生产率增长指数呈现出持续上升的态势,由2015 年的1.0000 增长至2019 年的1.1720,年均增长3.44%,2012—2018 年的均值为1.0739。此外,还可发现该折线图由平缓变得陡峭,说明高企整体累计全要素生产率增长指数上升速度呈现出由慢变快的态势。已有研究(许永洪等,2019;袁小慧和范金,2019;尹向飞和欧阳峣,2019)表明中国省市全要素生产率在2011 后增长基本维持在1%左右。这反映出各城市群高企引领和带动我国经济高质量发展。

图1 19 个城市群整体高企累计全要素生产率增长指数分布图
表3 汇报了19 个城市群高企全要素生产率指数。通过将各个城市群高企全要素生产率大小对比分析可知,经济发达城市群(如珠三角、川渝、长三角等)高企全要素生产率增长较慢,经济欠发达城市群(如呼包鄂榆、黔中、滇中等)高企全要素生产率增长则较快。这一研究结论与李静等(2016)、刘华军等(2018)以及蔺鹏等(2021)的研究结果相似。究其原因,全要素生产率与经济发展存在负向相关关系,即经济水平越高的城市群高企会较早进入高质量发展阶段,进而导致全要素生产率增长缓慢,经济欠发达的城市群高企发展质量提升空间较大,通过技术创新和效率改善就能明显实现全要素生产率增长。发达国家上市企业全要素生产率增速普遍低于发展中国家上市企业全要素生产率增速则为本文提供了很好的例证(许明和张其仔,2020)。
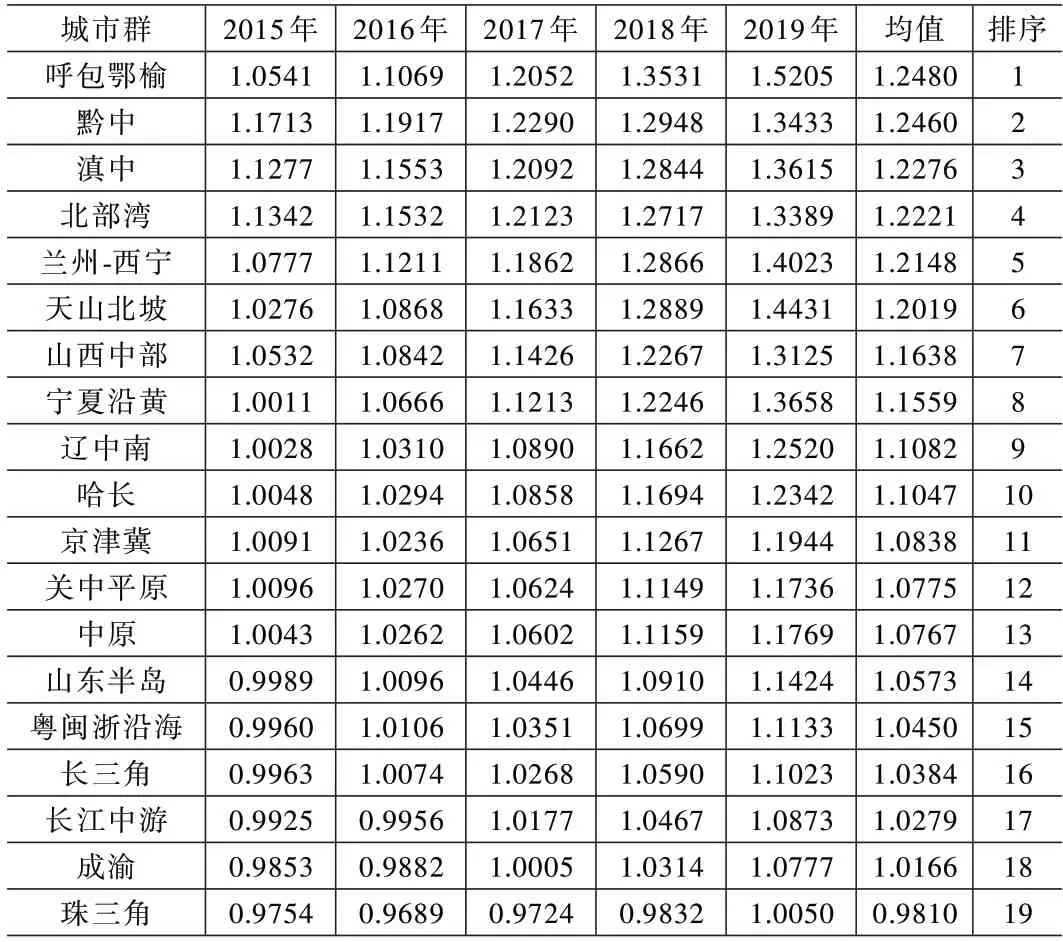
表3 19 个城市群高企累计全要素生产率指数
(三)19 个城市群高企整体全要素生产率区域差异
表4 汇报了2015—2019 年我国19 个城市群高企全要素生产率的总体Theil 指数、区域内Theil 指数和区域间Theil 指数,并计算了区域内差异和区域间差异对总体差异的贡献率。

表4 Theil 指数测算结果
第一,从总体Theil 指数的测算及结果分析来看,在样本考察周期内,19 个城市群高企整体区域差异均值为0.00830,呈现逐年持续上升趋势,由2015 年的0.00459 上升至2019 年的0.01367,年均增长49.46%。说明我国19 个城市群高企全要素生产率的整体区域差异呈现持续扩大态势,可能原因在于,不同城市群高企在地理位置、要素禀赋、创新能力、产业结构、开放合作、政策支撑等方面存在较大差异,由此引发各个城市群高企全要素生产率的空间差异扩大。这就要求在后续分析19 个城市群高企全要素生产率时空演进特征时,必须考虑空间关联因素。
第二,从Theil 指数的分解结果来看,在样本考察周期内,区域内Theil 指数和区域间Theil 指数演变趋势高度一致,两者均呈逐年上升趋势。就演变趋势而言,2015 年区域间差异为0.00072,2019 年区域间差异增长到0.00418,年均增长率120%;区域内差异由2015 年的0.00387 逐年上升到2019 年的0.00949,年均增长率为36.3%。由此可见,区域间差异增幅明显高于区域内差异的增幅,未来要关注区域间差异,并力争采取有效措施将其控制在一定范围内。就区域间差异与区域内差异大小而言,在样本考察期内,区域内差异明显高于区域间差异,区域间差异均值为0.00207,而区域内差异均值高达0.00623,区域内差异大约是区域间差异的3 倍。说明区域内差异是造成整体区域差异的根本原因,未来要想实现区域协同高质量发展,必须聚焦于不同城市群内部高企全要素生产率差异问题。
第三,从区域内、区域间差异对总体区域差异的贡献率来看,在样本考察周期内,区域间和区域内差异对总体区域差异的贡献率呈相反趋势,前者呈稳步上升态势,从2015 年的15.69%上升到2019 年的30.58%,区域间差异贡献率均值为22.67%;后者呈逐年下降态势,从2015 年的84.31%下降到2019 年的69.42%,区域内差异均值为77.33%。由于区域内贡献率和区域间贡献率是互补关系,从贡献率也可以看出,当前区域内差异是整体城市群高企全要素生产率差异的主要来源,但这种趋势正在减弱。
19 个城市群高企区域内Theil 指数的测算及结果分析。由于区域内差异是整体全要素生产率差异的主要来源,本文进一步按19 大城市群高企区域内差异均值进行排名,结果见表5。
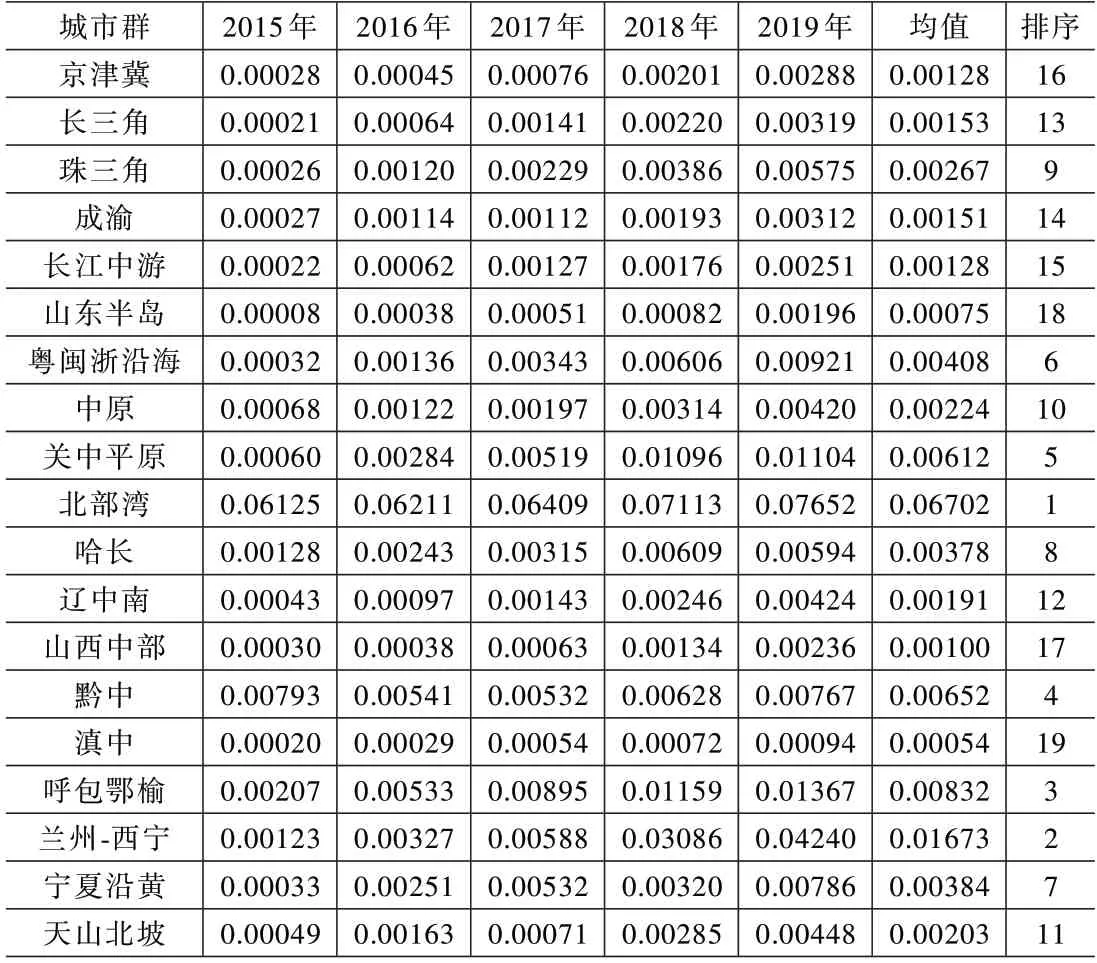
表5 19 个城市群高企全要素生产率Theil 指数区域内差异结果
从区域差异排名前列的地区来看,欠发达城市群高企区域内差异较为明显。例如,北部湾城市群的全要素生产率区域内差异最大,均值达到0.06702,历年的数据也显示了北部湾城市群高企的区域内差异正在逐年扩大。兰州-西宁城市群高企区域内差异排名第二,均值为0.01673,历年数值则显示出了“先上升后下降然后再上升”的波动趋势。呼包鄂榆城市群高企区域内差异排名第三,历年数值体现出区域内差异持续扩大趋势。而经济相对发展较发达城市群高企的区域内差异相对较小,如长三角、珠三角、京津冀和山东半岛城市群高企的区域内差异排名均处于相对靠后的位置,分别为第13、9、16 和18 名。说明相较于发达城市群高企,欠发达城市群高企全要素生产率增长的区域内差异相对较大。究其原因,发达城市群高企全要素生产率增速整体放缓,欠发达城市群内由于一部分城市内高企依托自身发展基础和优势,能充分发挥后发追赶优势,其全要素生产率增速较快,由此造成欠发达城市群高企全要素生产率增长的区域内差异更大。
四、19 个城市群高企全要素生产率增长的时空演进特征
(一)19 个城市群高企全要素生产率增长的时间演进特征
为进一步揭示19 个城市群高企全要素生产率增长率分布的时间演进特征,本文采用Kernel 核密度估计非参数方法分别绘制了2015—2019 年19 个城市群高企全要素生产率增长的密度分布图(图2~图21)。
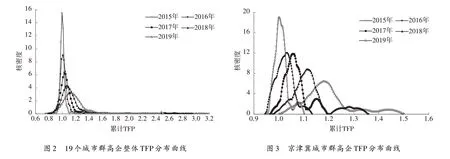

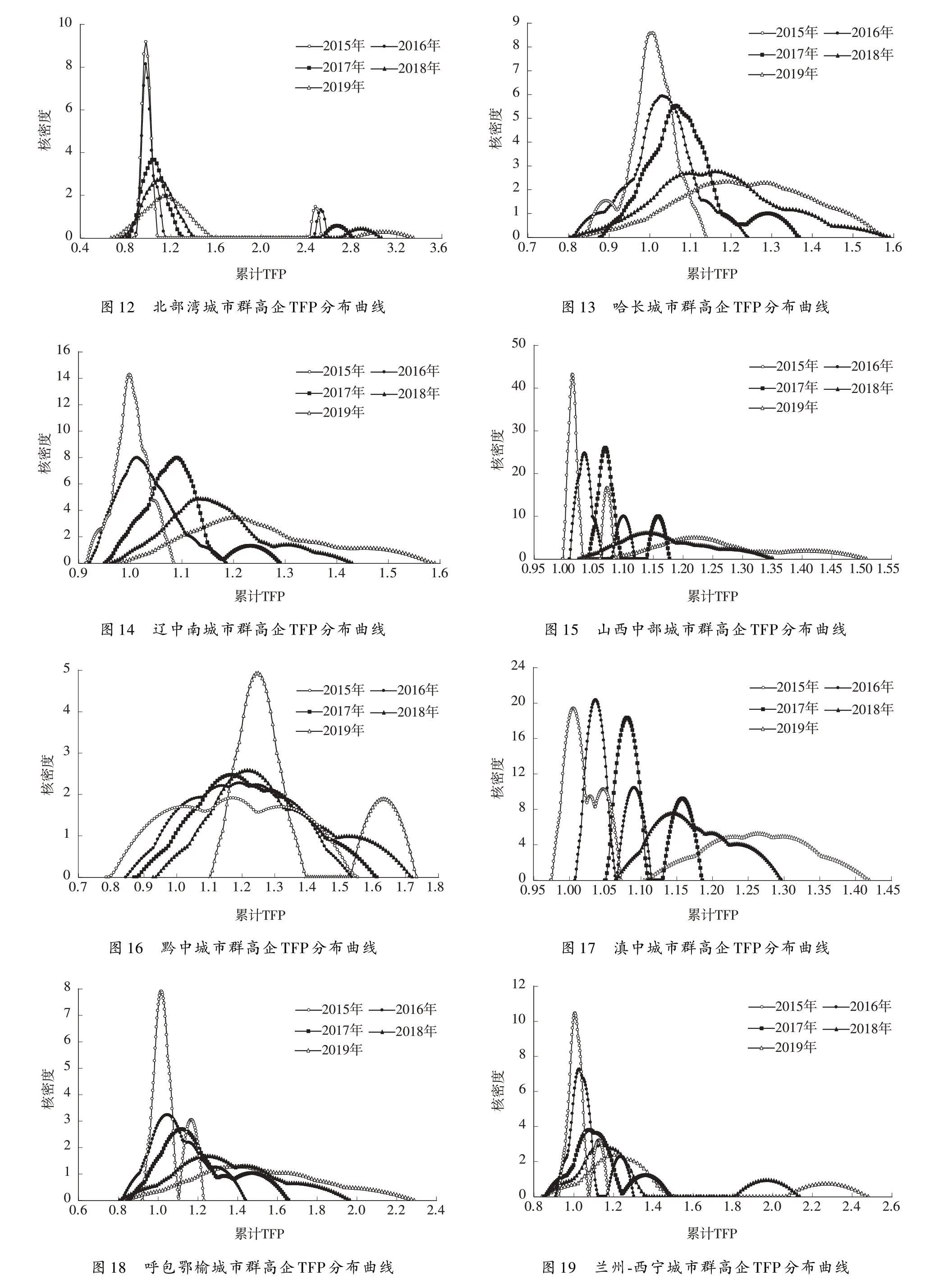

图2 19 个城市群高企全要素生产率分布曲线
第一,整体、各城市群高企全要素生产率增长的密度函数分布曲线中心点明显右移,呈现出靠右拖尾态势,说明整体、各城市群高企全要素生产率增长率呈现上升态势,这与前文所得结论一致。
第二,整体、京津冀、长三角、珠三角、成渝、长中游、山东半岛、粤闽浙沿海、中原、关中平原、北部湾、哈长、辽中南、山西中部、滇中、呼包鄂榆、兰州-西宁、宁夏沿黄等城市群高企全要素生产率增长的分布曲线宽度持续变宽,说明其高企全要素生产率增长的区域差异呈现扩大态势;黔中城市群高企全要素生产率增长的分布曲线宽度呈现出“缩小—扩大”态势,表明其高企全要素生产率增长的区域差异呈现“收敛—扩大”趋势;天山北坡城市群高企全要素生产率增长的分布曲线宽度呈现出“扩大—缩小—扩大”态势,表明其全要素生产率增长的区域差异呈现出“扩大收敛-扩大”趋势。
第三,整体全要素生产率增长的多极分化现象逐渐消失,最终以单极化现象呈现。京津冀城市群高企全要素生产率增长的分布曲线由一个主峰和一个侧峰转变为一个主峰和两个侧峰,且主峰峰值较高,侧峰峰值较低,表明京津冀城市群高企全要素生产率增长存在一定的梯度,呈现出多极分化现象;同时还可以发现其分布曲线峰值逐年下降,表明多极分化现象虽得到缓解,但多极分化现象并未得到有效控制。长三角城市群高企全要素生产率增长的分布曲线由一个主峰和一个侧峰转变为一个主峰和两个侧峰,且主峰峰值较高,侧峰峰值较低,表明长三角城市群高企全要素生产率增长水平存在一定的梯度,呈现出多极分化现象;北部湾、兰州-西宁、宁夏沿黄等城市群高企全要素生产率增长的分布曲线始终有一个主峰和一个侧峰,且主峰峰值较高,侧峰峰值较低,表明其全要素生产率增长水平存在一定的梯度,两极分化现象仍然明显;珠三角、长中游、中原、哈长、辽中南、山西中部、呼包鄂榆等城市群高企全要素生产率增长的分布曲线由一个主峰和一个侧峰转变为一个主峰,表明其全要素生产率增长的两极分化现象得到有效控制;成渝、山东半岛、关中平原城市群高企全要素生产率增长的分布曲线由一个主峰转变为一个主峰和一个侧峰,且主峰峰值较高,侧峰峰值较低,表明其全要素生产率增长水平存在一定的梯度,两极分化现象日益显著;天山北坡城市群高企全要素生产率增长的分布曲线始终保持着两个主峰和一个侧峰,且主峰峰值较高,侧峰峰值较低,表明其全要素生产率增长存在一定的梯度,多级分化现象严重;粤闽浙沿海、黔中城市群高企全要素生产率增长的分布曲线由一个主峰和两个侧峰转变为一个主峰和一个侧峰,且主峰峰值较高,侧峰峰值较低,表明其全要素生产率增长存在一定的梯度,存在两级分化现象;滇中城市群高企全要素生产率增长的分布曲线由一个主峰两个侧峰转变为一个主峰,表明其全要素生产率增长的多极分化现象得到了有效遏制。
(二)19 个城市群高企全要素生产率增长的空间演进特征
前面研究结论表明,空间位置分布及其关联关系都会对19 个城市群高企全要素生产率的转移规律和演进特征产生影响。因此,本文将采用空间Markov 链估计方法来揭示不同空间关联效应下相邻城市群高企的全要素生产率水平对本城市群高企的影响。
在采用空间Markov 链估计方法之前,需要对卡方检验结果进行分析,具体测算结果见表6,当选择时间跨度为1、2、3 年时,Q值均通过了1%显著性水平检验。这表明在不同的时间间隔条件下空间关联因素对19个城市群高企全要素生产率的状态转移产生了显著的影响。
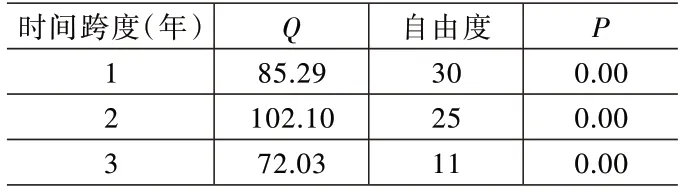
表6 空间Markov 链估计的卡方检验结果
本文按照全要素生产率大小将邻近城市群高企划分为“低、中低、中、中高和高水平”5 个等级,并以此来考察不同空间关联条件下各个城市群高企全要素生产率的空间演进特征,空间Markov 链估计见表7。总体而言,各个城市群高企全要素生产率的转移概率主要分布于对角线的右上方,呈现出非对称分布现象,这表明19 个城市群高企能够通过技术创新和效率改进来实现全要素生产率的整体跃升,突破中等水平路径限制,向更高水平迈进。较高全要素生产率水平的邻域环境对本城市群高企全要素生产率增长具有积极促进作用,且这种促进作用大小也直接取决于本城市群高企全要素生产率所处水平的高低。进一步具体而言,当本城市群高企为低水平、中低水平时,这种促进作用并不明显,但当本城市群高企为中高水平或高水平时,促进作用则相对明显,尤其是当邻近环境由中高水平提升至高水平时,本城市群高企向中高和高水平转移的概率显著提升。将不同时间跨度的转移概率矩阵对比可以发现,当时间跨度从1 年跨越至3 年时,不管在何种邻域水平环境下,低、中低、中、中高、高水平城市群高企保持平稳的概率变小,向上转移的概率明显增加。
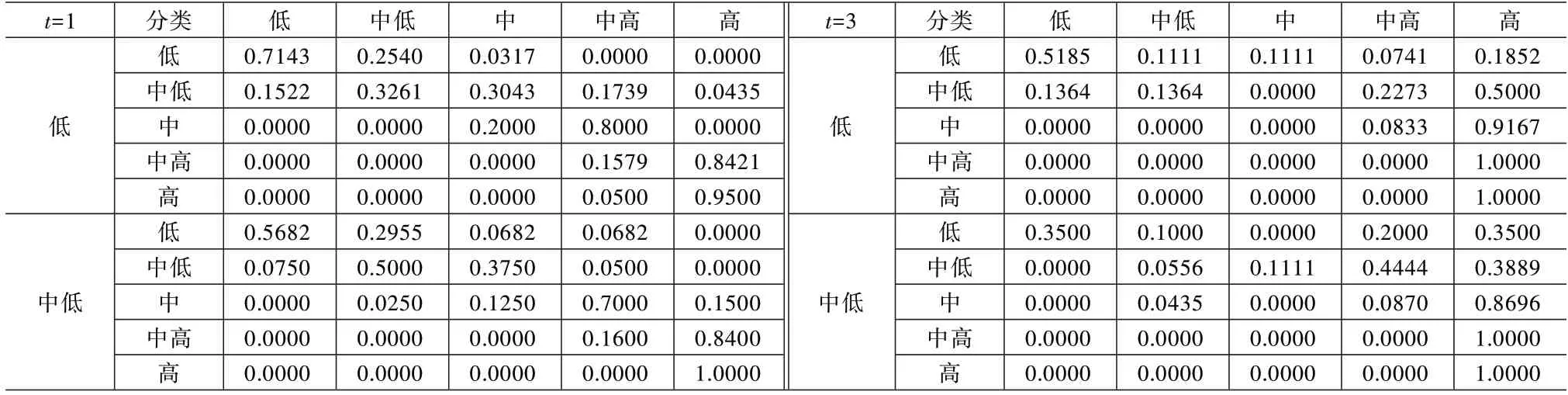
表7 19 个城市群高企全要素生产率的空间Markov 链估计结果(t=1、t=3)
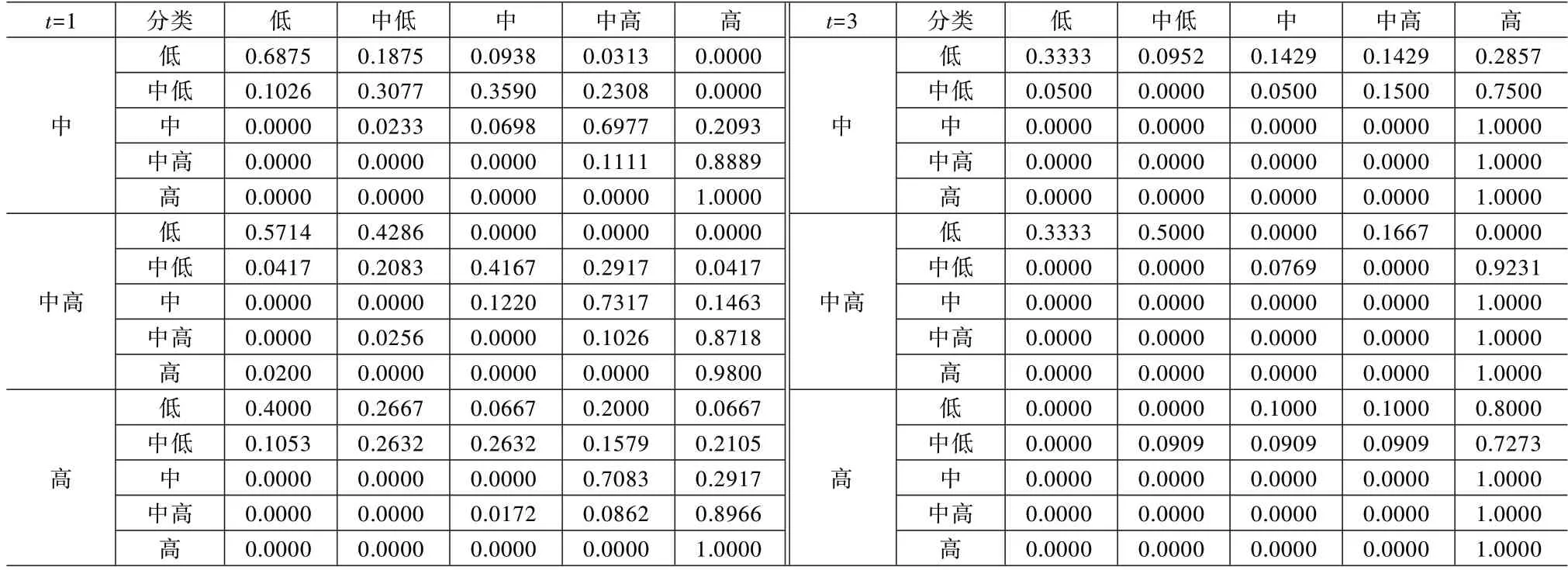
续表7
由上述分析可知,19 个城市群高企全要素生产率受空间地理因素的影响。换言之,某一城市群高企全要素生产率的演变会受到邻近城市群高企全要素生产率水平的影响。总体态势可以概括为:若某一城市群高企与高水平城市群高企邻近,其向上转移的概率会增加;相反,若某一城市群高企与低水平城市群高企邻近,其向上转移的概率会减小,向下转移概率明显增加。此外,随时间推移,在不同水平领域环境的影响下,19 个城市群向上转移的概率总体上有所增加。
五、结论与启示
本文基于2014—2019 年19 个城市群高企的经济投入和经济产出的面板数据,对19 个城市群高企全要素生产率增长水平、区域差异及其时空演进特征进行了实证研究。主要结论如下。
(1)19 个城市群高企全要素生产率呈现出持续上升态势,由2015 年的1.0000% 增长至2019 年的5.1188%,2015—2019 年的均值为3.44%,明显高于同时期中国省级层面的全要素生产率增长率(约1%),反映出各个城市群高企着力推动着我国经济增长方式由投资驱动向全要素生产率驱动转变,是引领和带动我国经济高质量发展的主要引擎。此外,不同城市群高企全要素生产率呈现出明显区域异质性,经济发达城市群(如珠三角、川渝、长三角等)高企全要素生产率增长较慢,经济欠发达城市群(如呼包鄂榆、黔中、滇中等)高企全要素生产率增长则较快。这一研究结论与李静等(2016)、刘华军等(2018)以及蔺鹏等(2021)研究结果相似。
(2)就整体区域差异而言,19 个城市群高企整体区域差异均值为0.00830,呈现逐年持续上升趋势,由2015 年0.00459 上升至到2019 年的0.01367,年均增长49.46%。从Theil 指数的分解结果来看,在样本考察周期内,区域内Theil 指数和区域间Theil 指数演变趋势高度一致,两者均呈逐年上升趋势,但区域间差异增幅明显高于区域内差异的增幅。未来要关注区域间差异,并力争采取有效措施将其控制在一定范围内。区域间和区域内差异对总体区域差异的贡献率呈相反趋势,前者呈稳步上升态势,后者呈逐年下降态势,区域内差异的贡献率约是区域间差异贡献率的3 倍,区域内差异是整体区域差异的主要来源。未来要想实现区域协同高质量发展,必须聚焦于不同城市群内部高企全要素生产率差异问题。
(3)整体、19 个城市群高企全要素生产率增长的密度函数分布曲线中心点明显右移,呈现出靠右拖尾态势,说明整体、各城市群高企全要素生产率增长率呈现上升态势。整体、京津冀、长三角、珠三角、成渝、长中游、山东半岛、粤闽浙沿海、中原、关中平原、北部湾、哈长、辽中南、山西中部、滇中、呼包鄂榆、兰州-西宁、宁夏沿黄等城市群全要素生产率增长的分布曲线宽度持续变宽,说明其高企全要素生产率增长的区域差异呈现扩大态势;黔中城市群高企全要素生产率增长的分布曲线宽度呈现出“缩小—扩大”态势,表明其高企全要素生产率增长的区域差异呈现“收敛—扩大”趋势;天山北坡城市高企全要素生产率增长的密度分布曲线宽度呈现出“扩大—收敛—扩大”趋势,表明其高企全要素生产率增长的区域差异呈现出“扩大—收敛—扩大”趋势。此外,19 个城市群高企全要素生产率增长率的极化现象各异。
(4)19 个城市群高企全要素生产率受空间地理因素的影响。换言之,某一城市群高企全要素生产率的演变会受到邻近城市群高企全要素生产率水平的影响。总体态势可以概括为:若某一城市群高企与高水平城市群高企邻近,其向上转移的概率会增加;相反,若某一城市群高企与低水平城市群高企邻近,其向上转移的概率会减小,向下转移概率明显增加。此外,随时间推移,在不同水平领域环境的影响下,19 个城市群向上转移的概率总体上有所增加。
根据以上结论,本文获得以下政策启示:
建设全国统一大市场。各地区应构建完善的要素市场,着力从市场资源配置效率、市场制度规则效率和市场信息效率等方面改进市场效率,尽可能降低由于要素市场垄断、地方保护和区域壁垒及各种规则不统一造成的市场效率损失;加强跨城市群的高企政策支持和政策联动,促进高企生产要素跨区域合理流动,提升要素资源跨区域利用效率。持续推动产业结构调整改善,各城市群可以通过组建区域高新技术企业集团来推动产业重组,保障产业链完整、安全,改善部分企业资源配置效率低下问题,促进经济资源向高效率企业集中,解决重复建设和产能过剩问题。
创新高企配套支持政策。改革高新技术企业认定管理办法,探索对高新技术企业实施分地区、分行业的政策精准扶持,对重点地区和领域高新技术企业适用力度更大的税率优惠;拓宽认定行业,针对性地出台一套申报高新技术企业的标准和考评体系。加快高新技术企业的科技成果转化,提高企业研发效率,支持高新技术企业充分利用国内外大数据资源,创新高新技术产品、技术和服务,提升高新技术制造业的生产管理效率,做好节能降耗,提高整体生产效率。
推动大中小企业融通发展。一是鼓励和支持大企业采购区内外无资产关联中小企业的科技产品和服务;二是提高中小企业在政府项目采购中的份额,鼓励大型企业与中小企业组成联合体共同参加政府采购;三是依托科技项目洽谈会、科技产品展览会或发布会等,大力宣传中小企业优质产品的推广应用,引导大型企业优先采购中小企业产品;四是鼓励和支持中小企业为多家大企业配套协作,规避运营风险,提升中小企业参与产业集群分工能力,制定出台产业转移、整合、协作的推进机制和考核机制,鼓励和支持中小企业加入高技术产业集群体系,按产品上下游进行纵向专业分工,推动形成优势互补、协调统筹、高质量发展的整体布局。
构建跨区域多主体合作网络。搭建立起跨区域高校院所、研发机构和企业之间有效的沟通合作机制,发挥出各自的优势,牵头形成产学研用协同创新生态,加强高校院所创新成果的对外扩散,最终将创新创业的科技成果转化为现实产品。鼓励高企重大创新平台、关键创业平台及新型研发机构的技术创新资源开放共享,通过采取市场化方式对外提供技术研发和人才培训服务。制定《大型科学仪器设施共享目录》,将使用财政资金购置的50 万元及以上的科学仪器设备纳入统一开放的国家网络管理平台,逐步形成跨部门、跨领域、多层次的网络服务体系。
