加权排列熵及其在矿化识别中的应用
2022-02-14罗文相
罗文相,万 丽,刘 慧
(1.广州软件学院,广东广州510990;2.广州大学数学与信息科学学院,广东广州510006)
熵是系统复杂度的一种度量,可用于时间序列动力学状态识别。在信息论建立后,关于熵的理论和应用得到了迅速的发展。近年来,在信息熵的基础上,提出了新的熵,如:近似熵、排列熵、样本熵等[1-3]。加权排列熵[4](weighted permutation entropy,WPE)是Fadlallah在2013年针对排列熵在计算过程中没有考虑时间序列中的幅值信息而提出的一种改进方法,具有较好地抗噪抗干扰能力,其算法简单、可操作性强,能有效放大时间序列的微小变化,广泛应用于信号突变检测、随机信号分析等方面,并在机械故障诊断、医学等领域取得良好的应用效果[5-7]。
成矿系统是地球物质系统的一个重要组成部分,成矿系统及其动力学是地球科学前沿研究的热点之一。矿床的形成往往经历了多种地质作用叠加、多期次演化和漫长的复杂过程,因此是一个时间域和空间域跨度都非常大的非线性复杂地质巨系统[8]。成矿系统的演化是时间发展、空间展布和成矿作用的相互作用,在时间和空间上不可分割。由于时间演化的不可再现性和长期性,可以依据时空演化的相关性,通过对空间系列数据的研究,获得时间上动力学过程的演化规律。但在地质实际中,常常不能确定成矿系统的动力学方程,只是得到实际的观测数据,如成矿元素含量序列[9]。因此,需要引入新的非线性动力学指标来刻画成矿元素含量序列的特征。
本文将检验加权排列熵对不同动力学的识别的有效性,并将其引入到成矿元素含量序列的非线性特征的分析中,探讨成矿元素含量序列的复杂性与矿化强度的关系,为揭示隐藏在成矿元素含量序列背后的动力学特征提供新方法。
1 理论与方法
1.1 加权排列熵算法
设长度为N的时间序列X={x(n),n=1,2,… ,N},对时间序列X进行相空间重构,得到N-(m-1)τ行,m列的矩阵XK:
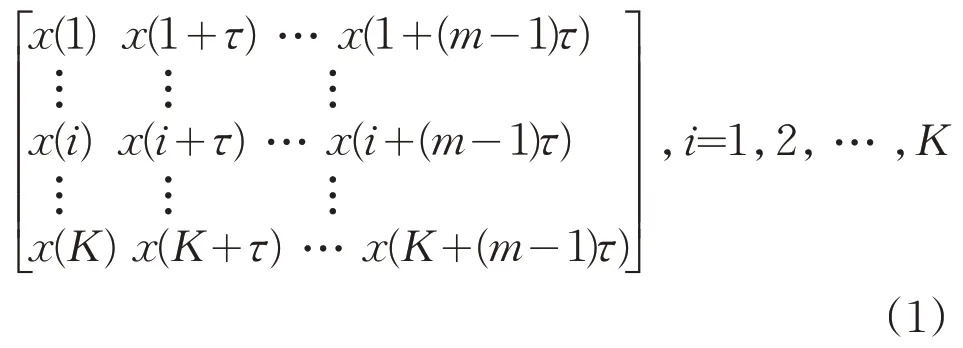
其中,K=N-(m-1)τ,m是嵌入维,τ是延迟时间。矩阵XK中的每一行为一个重构分量,共有K个。将第i个重构分量Xi=(x(i),x(i+τ),… ,x(i+(m-1)τ)按照升序重新排列,得到:
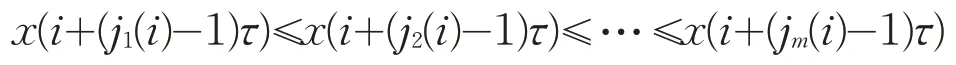
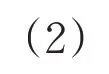
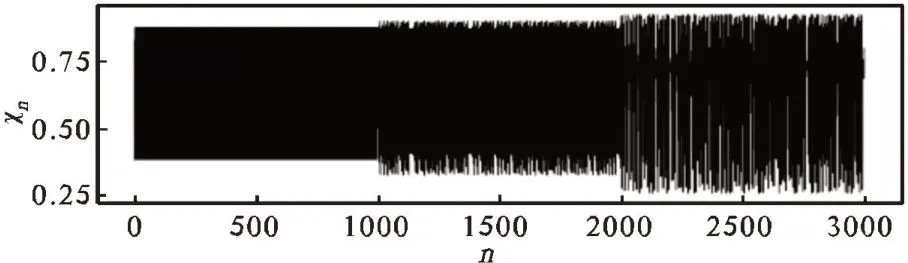
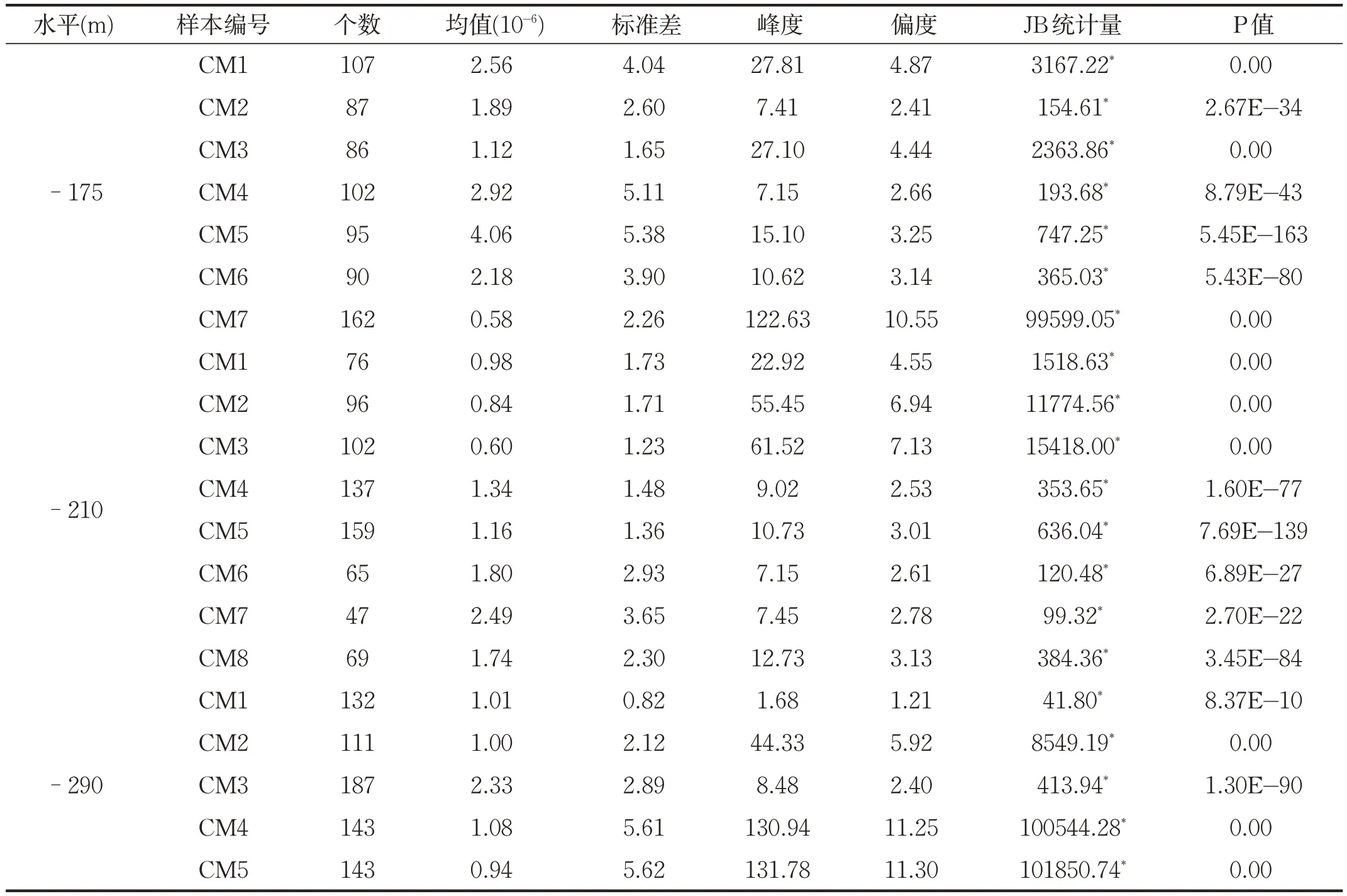
其中i=1,2,…,K,j1(i),j2(i),…,jm(i)表示元素所在重构分量中列的索引。若元素相等,则按照元素索引的大小进行排列。因此,矩阵XK中的每个重构分量重新按照升序排列,得到一个K行m列的符号序列矩阵。记πi=(j1(i),j2(i),…,jm(i)),i=1,2,…,K,πi为(1,2,…,m)的某一种排列,显然,m个元素最多有m!种不同排列,记为Π。以时间序列{7,6,5,8,6}为例,当m=3,τ=1时,得到的第一个重构分量为(7,6,5),由于xt+2 记πr为πi中某种排列,其中0 其中,wr是重构分量Xj的权值,由Xj的方差表示: WPE是排列熵的一种改进算法,它考虑了包含在时间序列中的幅值信息,表达式定义为: 其中,log 表示为以2 为底的对数。若对WPE(m)进行归一化处理,可得: 加权排列熵在计算某种排列的概率时考虑了与其相对应的重构分量的幅值信息,能充分反映时间序列的细致特征。 为检测加权排列熵对不同动力学结构的指示作用,构造理想时间序列IS,该序列由Logistic 映射[11]产生,长度为3000,其迭代方程如下: 其中λ∈ [0,4],表示生长率。取初始值x1=0.7,理想时间序列IS 的前1000 个数据的参数为λ=3.5,处于四周期状态,中间1000 个数据的参数为λ=3.6 和后1000 个数据的参数为λ=3.7,两者均处于混沌状态,其演化曲线由图1 给出。从IS 的构造可知,在n=1001时,系统的演化由四周期变为混沌状态,变化幅度比较大;在n=2001时,系统的演化由较低的生长率3.6变成较高的生长率3.7。IS 序列前部分的复杂度比中间部分的复杂度低,中间部分的复杂度比后部分的复杂度低,且前部分与中间部分的复杂度差距会明显大于中间部分与后部分的复杂度差距。 图1 理想时间序列IS 图2 IS序列的WPE值 取滑动窗口为150,滑动步长为1,嵌入维m=3,延迟时间τ=2,对时间序列IS进行加权排列熵检测,结果由图 2 给出。在n=1000 和n=2000 前后,WPE 值分别呈现出三种不同的稳定状态。前部分的WPE 值处于较低水平,后部分的WPE 值处于较高水平,而中间部分的WPE值处于两者之间,由熵的物理意义可知前部分数据的复杂度比中间部分的复杂度低,中间部分数据的复杂度比后部分的复杂度低,与理想时间序列IS的构造基本一致,说明加权排列熵的改变和大小的差异可以用来指示时间序列的动力学行为。 选取研究区为胶东大尹格庄金矿,该金矿是典型蚀变岩型矿床,位于招(远)—平(度)断裂带的中段。围岩蚀变主要包括钾长石化、硅化、绢云母化、绿泥石化、(黄铁)绢英岩化、碳酸盐化等,其中黄铁绢英岩化是矿区最发育的一种中温热液蚀变,也是金矿化关系最密切的蚀变作用。主要开采-500~-140m之间的工业矿石,矿床地球化学研究证实,成矿流体多期活动,具有幔源、岩浆热液与大气降水等多种来源途径[12-13]。 本文选取大尹格庄金矿-175m、-210m 和-290m中段共20条勘探线(其中-175m中段7条,-210m中段8条,-290m中段5条)中的Au元素刻槽含量数据序列作为研究对象,分别记为CMi(i 为样本序号)。对这20条勘探线中的Au 元素含量数据序列进行基本的统计描述和采用雅克—贝拉检测(Jarque-Bera Test,JB 检测)进行正态性检验,统计结果见表1。 表1 Au元素含量数据的统计描述和正态检验 在95%的置信度下,统计结果显示Au元素含量数据分布为明显的尖峰、右偏分布,JB统计值所对应的概率均小于0.05,表明这20条勘探线的Au元素含量序列显著呈非正态分布。因此,那些基于正态分布假设前提的传统方法难以准确地描述其非线性的特征。 使用加权排列熵刻画Au元素含量序列的复杂度,取嵌入维m=3,延迟时间τ=1,分别计算大尹格庄金矿20条勘探线Au元素含量序列的加权排列熵值。同时,根据Au元素含量值,将勘探线所对应的矿化强度由强到弱分为4个不同的矿化等级[14]。大尹格庄金矿Au元素的工业品位是2g/t(2×10-6),统计勘探线元素含量大于边界品位的个数,得出元素含量大于边界品位的个数在该勘探线的比例p,记4种不同的矿化等级为:(Ⅰ)强矿化区,比例p大于33%,矿体部分连续;(Ⅱ)中等矿化区,比例p为20%~33%,矿体区域间断出现,变化幅度大;(Ⅲ)弱矿化区,比例p为10%~20%,难以圈定矿体区域,或为矿体尖灭末端;(Ⅳ)无矿化区,比例p小于10%。大尹格庄金矿20条勘探线所对应的加权排列熵值与矿化等级如表2所示。 表2 Au元素的加权排列熵值与矿化等级 由表2 可知,属于强矿化区的勘探线有-175m 中段的CM1、CM5,-210m中段的CM7,和-290m中段的CM3,共4条勘探线,其Au元素含量序列的WPE值分别为0.8123、0.9103、08871、0.9272。中等矿化区的勘探线有-175m中段的CM2、CM4、CM6,-210m中段的CM4、CM6 和 CM8,共 6 条勘探线。弱矿化区的勘探线有-175m 中段的CM3,-210m 中段的CM5,-290m中段的CM1和CM2,共4条勘探线。无矿化区的勘探线有-175m 中段的 CM7,-210m 中段的 CM1、CM2、CM3,-290m中段的CM4和CM5,共6条勘探线。 根据Au 勘探线矿化等级与加权排列熵值进行对比分析,其结果如图3所示。 图3 Au元素矿化等级与加权排列熵值 图中显示,得到的WPE值的大小与不同矿化等级之间存在一定的关联,其WPE 值由大到小依次为:中等矿化>强矿化>弱矿化>无矿化,且强矿化、中等矿化和弱矿化之间的相邻差距是大致相近的,而无矿化和弱矿化之间的差距明显大于前者。表明在无矿化区Au 元素含量绝大部分集中在低含量值(低于Au 元素的边界品位2g/t),没有或几乎没有发生金矿化,Au元素含量相对有序,复杂性较低,其对应的WPE 值较小。随着矿化强度的增加,Au元素含量序列的复杂度发生不同的改变。在弱矿化区,Au元素的含量以低含量值为主,但有小部分(10%~20%)含量值是超过边界品位的,因此复杂性相对无矿化区有所增强,WPE 值也有所增大。在中等矿化区,矿区区域间断出现,Au元素含量序列发生间断性混沌,而加权排列熵考虑了时间序列的幅值信息,放大了这种间断性特征,因此复杂性最强,WPE 值最大。在强矿化区,Au元素含量序列的高含量值占比最高,序列趋向于高品位的局部聚集,其复杂性相对于中等矿化有所减弱,WPE 值也有一定的减小。Au元素含量矿化等级与WPE的对比结果与用其他非线性指标对Au 元素含量序列复杂性的研究结论基本一致[15]。 (1)通过Logistic模型检验了加权排列熵是识别不同动力学状态的有效指标之一,能有效放大时间序列的微小变化,为进一步地质数据的应用提供了理论依据; (2)通过对大尹格庄多中段共20条勘探线的Au元素含量序列的加权排列熵分析和比较,发现不同矿化强度的元素含量序列的加权排列熵值存在差异,说明不同矿化强度的元素含量序列具有不同的复杂度,这种差异性可用于矿化识别,为进一步定量刻画矿床富集程度和圈定有利成矿靶区提供参考。
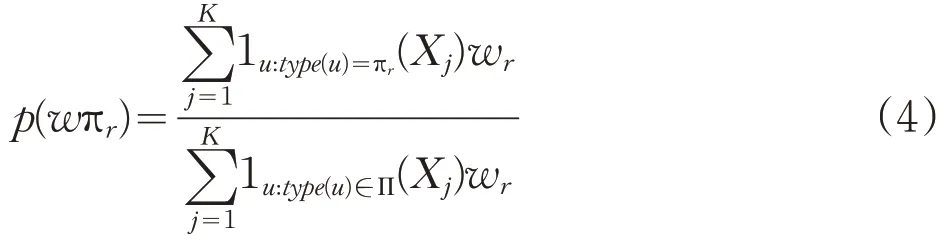

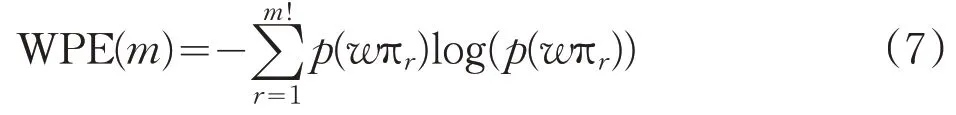
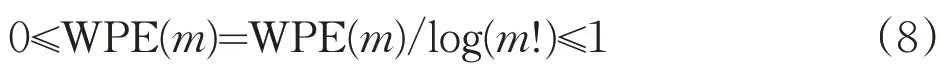
1.2 加权排列熵的动力学识别检验
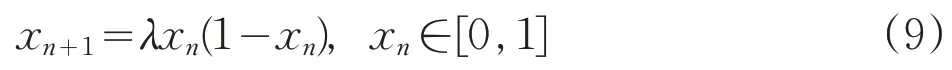

2 加权排列熵在矿化识别中的应用
2.1 样本来源与基本统计
2.2 计算过程与讨论


3 结论
