计及风电功率相关性的微电网日前随机优化调度方法

姜宇，陈翔宇，傅守强

（国网冀北电力有限公司，北京市 西城区 100054）

0 引言

为了集成分布式可再生能源并实现新能源本地消纳目标，微电网在近年来受到人们的高度关注[1]。风电等可再生能源受天气影响大，预测系统往往存在较大误差，而微电网的日前调度需要依靠日前预测信息[2]。因此，如何对预测误差精确建模，以最大限度地降低预测误差的影响，对微电网在实际运行中提高经济性有着至关重要的作用。

确定性优化形式简单，但调度结果受不确定因素影响较大[3]。鲁棒优化和随机优化是两种常用的不确定优化方法[4]。鲁棒优化使用不确定集来描述随机变量的可能范围，并最小化随机变量在不确定集内最恶劣场景的运行成本，但鲁棒优化的结果往往存在一定的保守性[5]。虽然一些文献通过考虑相关性等方式增加调节参数来控制保守度，但这些参数在实践中一般难以确定[6-8]。随机优化基于不确定变量的概率分布，旨在寻找所有场景下期望运行成本最小的调度方案，而其性能取决于能否找到合理描述随机变量分布的场景[9]。因此，如何准确地对随机变量的分布特性进行建模是一个关键问题。

文献[10]在电热联合系统日前经济调度中假定风电预测误差服从正态分布，通过采样和场景削减得到随机场景。文献[11]使用模糊C均值 聚类综合质量法对风电及光伏的出力场景进行聚类，在随机优化调度模型中考虑条件风险价值规避潜在风险。文献[12]采用分布鲁棒优化，从风电预测误差历史数据中提取矩信息等概率信息，相比鲁棒优化降低了保守度。这些文献考虑了可再生能源出力的不确定性，但是没有计及预测误差的相关性对场景的影响。

文献[13-15]考虑了多风场出力的相关性，引入Copula函数对多风场出力的联合分布进行建模，得到更加合理的风电出力场景，再通过随机优化求解调度问题。文献[16]则基于混合Copula函数及连续马尔科夫链模型生成考虑风电场的时空相关性的典型风速场景，并采用了改进机组组合的两阶段调度模型。但上述研究均未考虑风电功率预测误差与预测值的条件相关性，即预测误差的绝对值随着预测值的增大而更可能偏大[17]。在针对风电功率第二日的潜在场景进行评估时，考虑预测误差与预测值的相关性有利于进一步提升场景建模的精度。

面向微电网日前优化调度中所面临的风电功率预测精度难以保障、出力存在强不确定性的技术挑战，本文基于条件正态Copula（conditional normal copula，CNC）方法，构建了计及风电功率相关性的随机优化模型。CNC模型能够对风电预测误差时间相关性及其与预测值的条件相关性进行有效建模，并能够根据日前预测值生成该条件下的风电功率样本，聚类之后可得到风电功率场景。将得到的场景应用于随机优化模型中，可提升微电网日前调度方案的经济性。

1 风电功率样本点生成

1.1 多元正态Copula

Copula理论用于描述多元随机变量之间的相关性。Copula函数可以将随机变量的联合分布解耦为边缘分布和相关关系分别建模，其中边缘分布描述变量的随机性，而Copula函数仅描述相关性。对于已知的边缘分布类型的随机变量，可通过参数估计得到边缘分布函数；对于边缘分布未知的随机变量，可用经验分布作为边缘分布。常用的Copula函数主要有多元正态Copula函数、多元t-Copula函数和阿基米德Copula函数。常用的阿基米德Copula函数包括Gumbel Copula、Clayton Copula和Frank Copula函数。多元正态Copula函数形式简单、性质优良，对多元随机变量具有较好的拟合效果，且能够求得条件分布的简化形式，故本文采用多元正态Copula描述风电功率预测误差的时间相关性及其与日前预测值的条件相关性。

根据多元正态Copula可以得到风电功率预测值与预测误差的联合概率密度函数

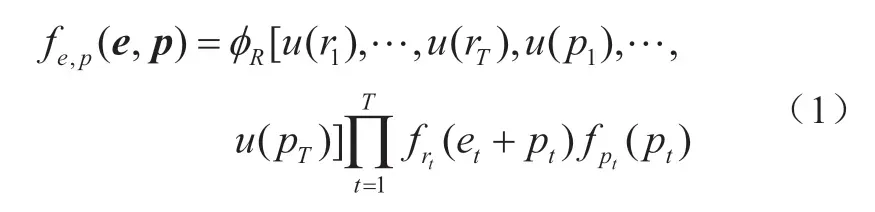
式中：rt、pt和et分别表示t时段风电功率的实际值、预测值和预测误差；et=rt-pt，t=1, 2, …,T，T为调度周期内总的调度时段数。和是多元正态Copula的中间变量，Φ0(·)、F(·)和f(·)分别表示标准正态分布、边缘分布和概率密度函数。φR(·)是以R为相关性参数矩阵的标准多元正态分布函数，其中

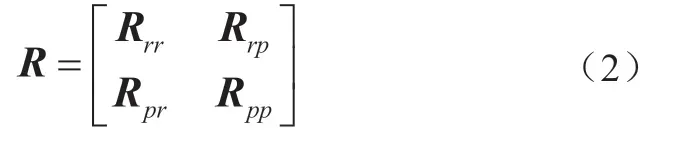
式中，

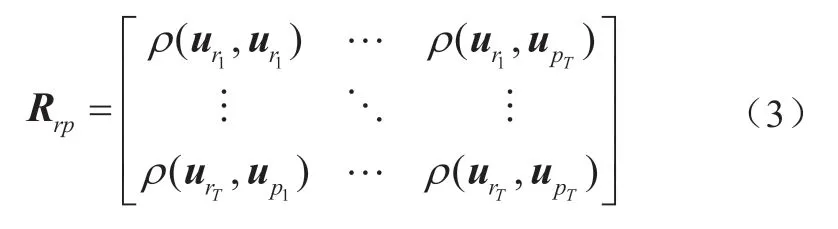
1.2 条件多元正态Copula采样

由式（1）和条件分布的性质可以得到已知风电预测值条件下预测误差的概率密度函数

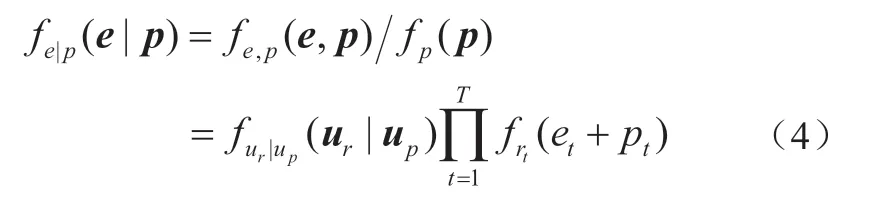
式中，ur|up为多元正态分布的条件分布，仍服从多元正态分布，即其中[18]

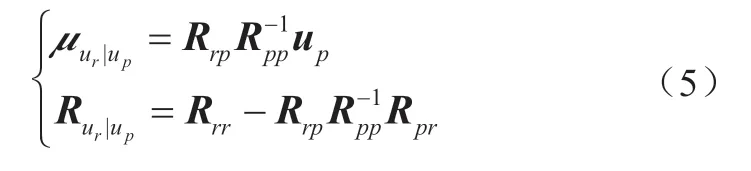
据此，我们可以根据风电功率日前预测值得到风电功率的样本点，具体步骤如下：

1）根据风电功率实际值和预测值的历史数据获得边缘分布F(·)和式（2）中的相关性矩阵R。

2）根据日前预测值pt计算

3）根据式（5）计算条件分布ur|up的期望值向量μur|up和协方差矩阵Rur|up。

4）对多元正态分布ur|up采样，得到大量u(rt)的样本，最终计算出大量计及风电功率相关性的风电功率样本以便在第3章通过K-means聚类得到随机优化所需的场景。

2 微电网确定性优化模型

典型的微电网结构如图1所示，微电网控制中心根据分时电价和对风电功率的预测，提前制定微电网的日前储能充放电计划、可控分布式电源的发电计划、灵活性负荷的需求响应方案以及微电网与配电网的交换功率计划等，以便在满足负荷的电能需求和系统约束的前提下，尽可能地降低运行成本。确定性模型是随机优化模型的基础，因此先引入确定性优化模型。

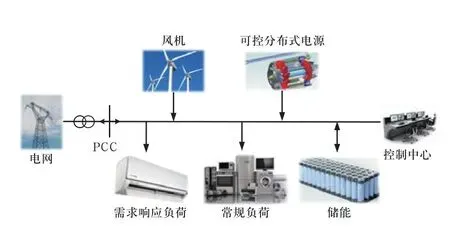
图1 微电网结构图Fig.1 Structure diagram of microgrid

2.1 目标函数

确定性优化模型的目标是最小化微电网第二天的总运行成本，即

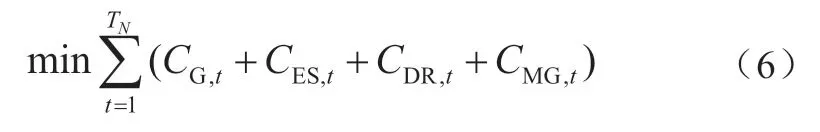
式中：TN为一天的调度时段数；Δt为调度周期。在日前调度中，一般取Δt=1 h，TN=24；CG,t、CES,t、CDR,t和CMG,t分别为可控分布式电源、储能系统、需求响应负荷和微电网购售电在t时段的成本，计算方法为：

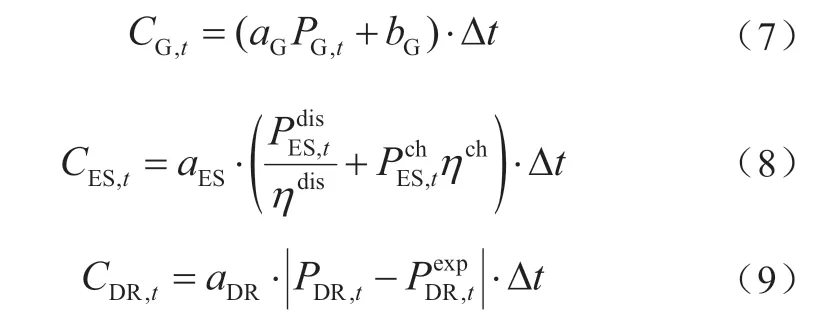
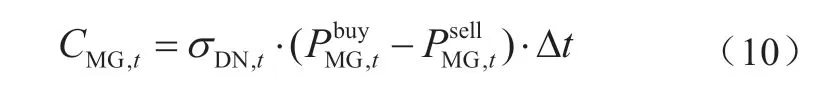
式中：PG,t表示可控分布式电源t时段的输出功率；aG和bG为成本系数；表示储能放电/充电功率；aES为储能单位充放电成本；ηdis/ηch是储能的放电/充电效率；aDR是需求响应负荷单位调度成本；是t时段需求响应负荷的实际调度功率/期望功率；σDN,t为t时段的日前交易电价；为微电网在t时段购电/ 售电功率。

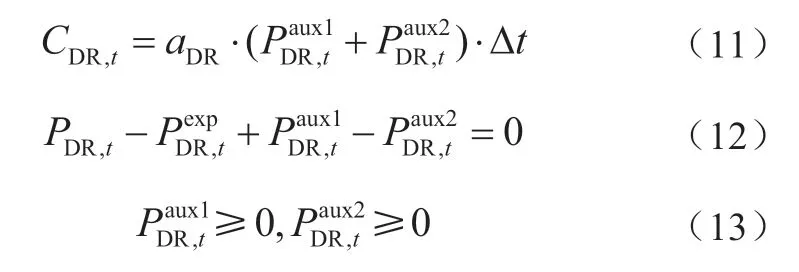
2.2 约束条件

在最小化运行成本的同时需要满足如下运行约束：

2.3 紧凑形式

微电网确定性优化模型的紧凑形式为：

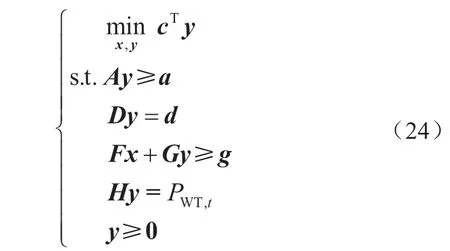
式中：x、y为优化变量，即

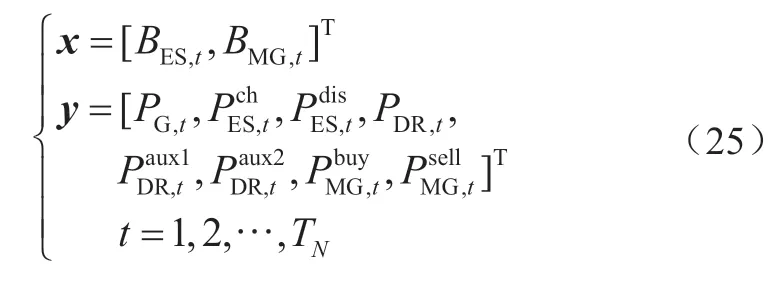
c为目标函数式（6）中的系数列向量。A、D、F、G、H分别为约束中变量的系数矩阵；a、d、g为约束中的常数列向量。式（24）的约束条件中，第1行为仅含y的不等式约束，对应式（14）、（18）、（19）；第2行为仅含y的等式约束，对应式（12）、（17）、（20）；第3行表示包含x和y的不等式约束，对应式（15）、（16）、（22）、（23）；特别的，第4行等式约束为式（21）中的功率平衡约束。在确定性优化模型中，风电预测功率的不确定性没有被考虑，直接作为优化调度中风电的输出功率。

3 微电网CNC随机优化模型

可再生分布式电源的出力具有很强的随机性，同时相应的功率预测系统不可避免地存在预测误差，如果在实际调度中不能很好地考虑预测误差，可能导致提前制定的微电网优化调度方案不可行或不经济。CNC随机优化模型根据不确定变量的概率分布特性更加精确地评估可再生分布式电源在第二日可能的出力场景，从而保障微电网在第二日实际运行时能最大限度地降低预测误差的影响。

根据第1节中CNC方法产生的风电功率样本点rt，使用K-means聚类方法得到K类场景，聚类中心为PWT,t,k。随机优化的目标函数是根据不确定变量在各场景下的概率，最小化各个场景下日总期望运行成本，即

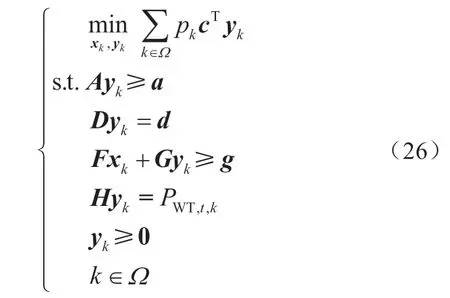
式中：Ω为K类场景的集合；pk为第k个场景出现的概率；优化变量xk和yk为第k个场景下的优化变量x和y。相应地，约束条件应当在风电功率的各个场景下都得到满足。该模型为混合整数线性规划模型，可通过常规的确定性优化方法进行求解。由于将优化变量在各场景下可能取值不同，因此求解完成后需要通过期望函数进行转化：

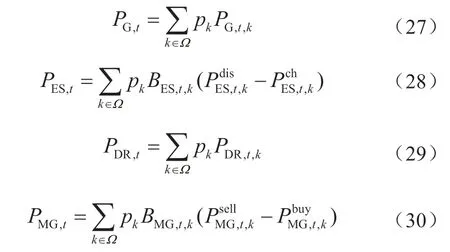
式中：PES,t为储能功率（储能放电为正）；PMG,t为联络线功率（微电网售电为正）。

4 算例分析

算例使用北爱尔兰某风电场的风电数据[19]，由2019年8月—11月的风电功率训练CNC模型，并用12月的数据进行微电网CNC随机优化模型的效果进行测试。

4.1 风电功率预测误差相关性分析

对风电功率的时间相关性和风电功率预测误差与预测值的条件相关性分别进行分析。

图2展示了风电功率的时间相关性，即各时段风电功率预测误差的线性相关系数，横、纵坐标轴表示各时段，不同颜色代表预测误差线性相关系数的大小，图例展示了对应的数值。可以看出，相邻时段的风电功率预测误差表现出较强的时间相关性。考虑时间相关性能够有效推理出风电场景中的经常发生的持续偏差场景，而不是预测误差忽大忽小的场景，从而得到在各种可能场景下期望最优的调度方案。

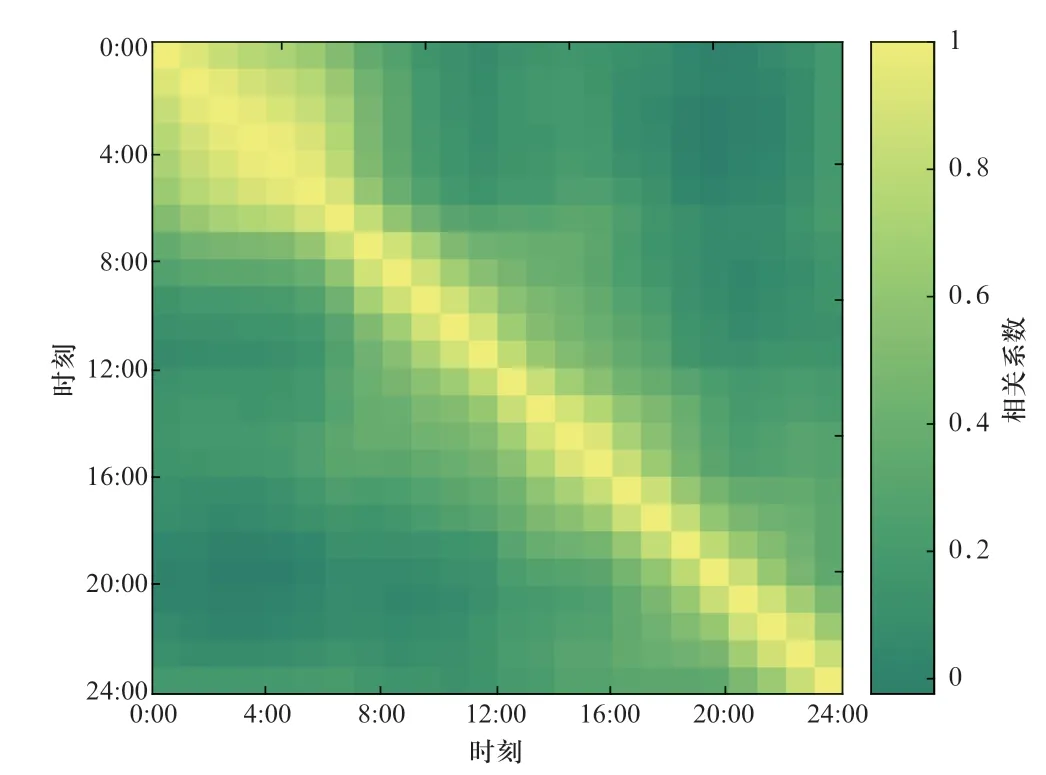
图2 风电功率预测误差时间相关性Fig.2 Temporal correlation of wind power forecast error

图3分析了风电功率预测误差与预测值的条件相关性。选取风电功率预测值为0.05 pu、0.15 pu、0.35 pu附近的预测误差数据，范围是±0.03 pu，从图中可以看出，当预测值较小时，预测误差较小且集中分布；而预测值较大时，预测误差相对更大且更分散。因此，需要根据不同的日前预测值得到不同的预测误差的分布，从而在日前调度中得到更合理的风电功率场景。

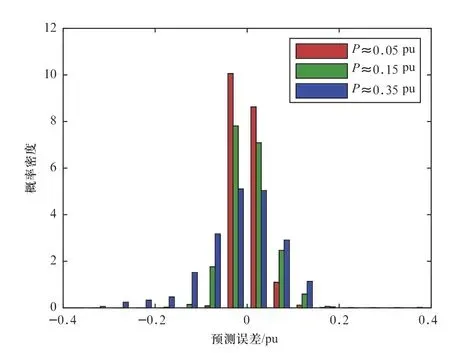
图3 不同风电功率预测值下预测误差的概率密度图Fig.3 Probability density of forecast error under different forecast of wind power

4.2 微电网随机优化结果分析

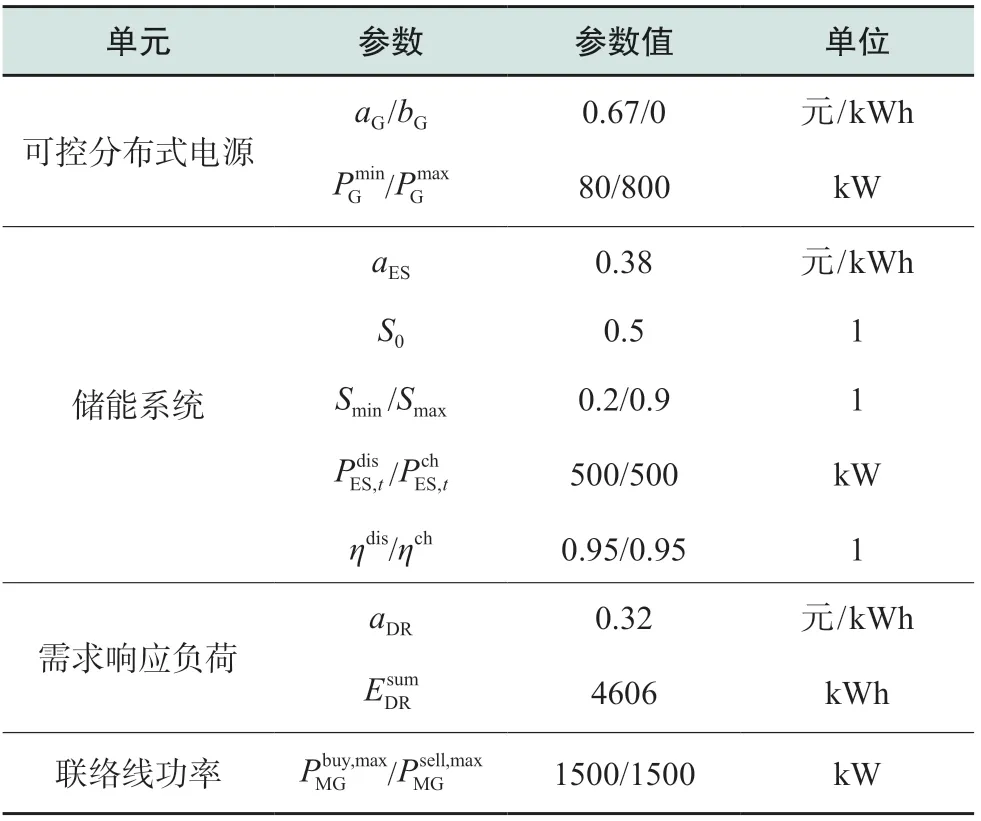
表1 微电网运行参数Table 1 Operation parameters of microgrid

微电网运行参数如表1所示。微电网的日前交易电价为阶梯电价，如图4所示。图5为常规负荷功率及需求响应负荷期望功率曲线。需求响应负荷在各个时段的功率可调度范围设为该时段期望功率的60%～140%。

根据误差平方和（SSE）确定聚类的场景数，使用K-means聚类方法生成风电功率场景，图6为场景数与SSE的关系。从图中可以看出，SSE随场景数的增加而减少，而当场景数为7时，SSE由快速减少变为缓慢减少。因此，我们将聚类的场景数定为7。

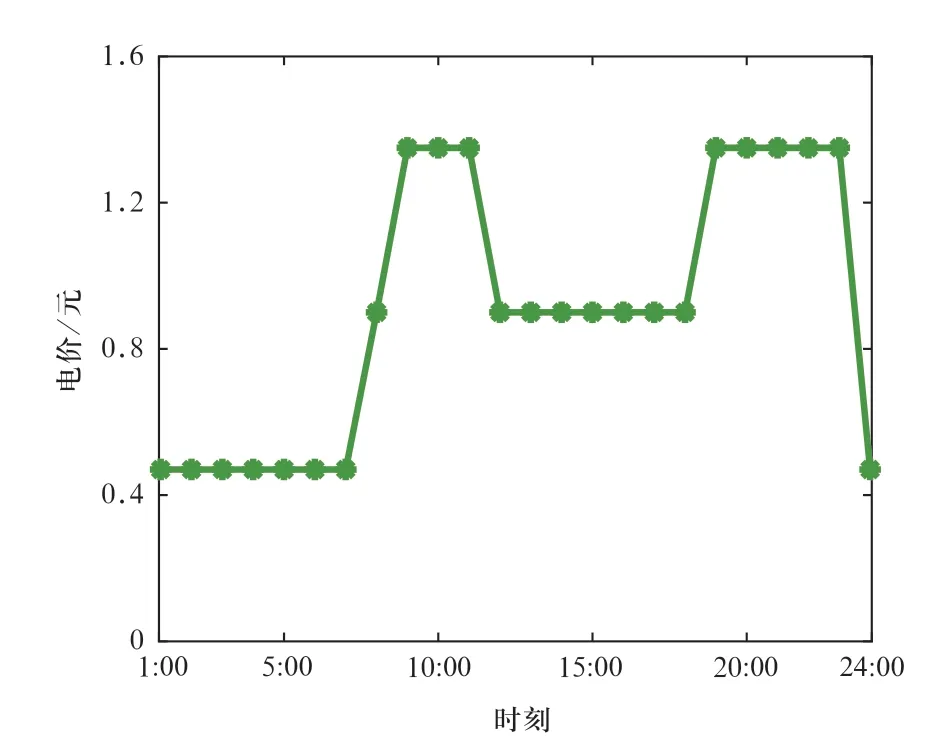
图4 日前交易电价曲线Fig.4 Day ahead trading price curve

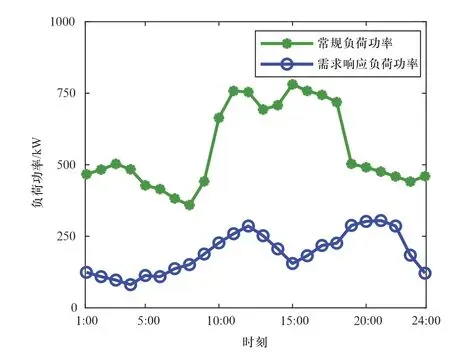
图5 常规负荷功率及需求响应负荷期望功率曲线Fig.5 Conventional load power and demand response load expected power curve

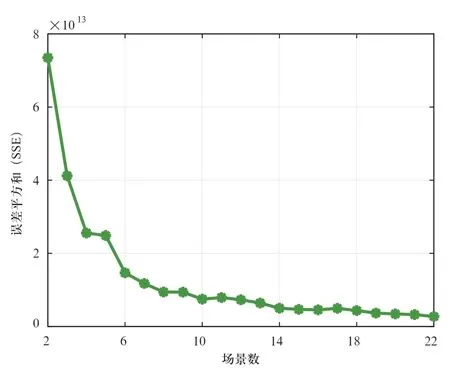
图6 SSE与场景数的关系Fig.6 SSE with the number of scenes

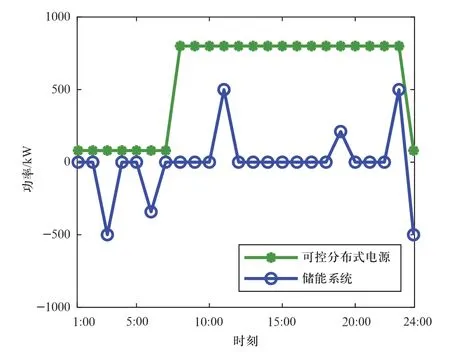
图7 可控分布式电源输出功率及储能充放电功率曲线Fig.7 Controllable distributed power and energy storage charge-discharge power curve

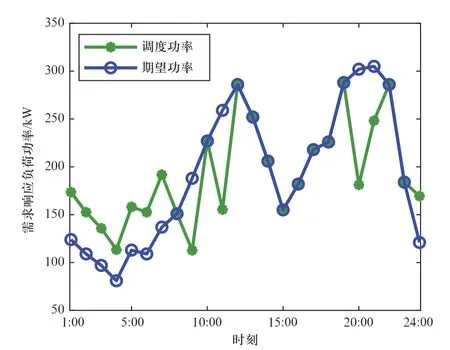
图8 需求响应负荷期望/实际功率曲线Fig.8 Expected/actual power curve of demand response load

随机优化的调度结果如图7～图8所示。图7展示了可控分布式电源及储能的调度结果，由于8:00—23:00的微电网售电电价高于可控分布式电源的发电成本，因此可控分布式电源按最大输出功率发电；而在1:00—7:00及24:00，微电网售电电价低于可控分布式电源的发电成本，因此可控分布式电源以最小输出功率发电，从而最小化微电网的成本。储能在电价低谷时（3:00、6:00及24:00）充电，在电价高峰时（11:00、19:00及23:00）放电，通过削峰填谷实现微电网套利。图8展示了微电网通过需求响应负荷功率平移降低电网运行成本的方式。与储能削峰填谷的原理类似，调度策略将需求响应负荷在电价高峰（9:00、11:00及20:00）的负荷需求平移至电价低谷时段（1:00—7:00及24:00），降低了负荷用电成本。综上，微电网随机优化的调度结果合理，能够充分调度可控分布式电源、储能、需求响应负荷等资源来最小化微电网的运行成本。

4.3 与其他模型的结果对比

考虑如下5种优化调度模型的结果对比：

Case 1：确定性优化模型。不考虑预测偏差，直接使用风电功率日前预测值进行优化调度。

Case 2：低置信度鲁棒模型。根据风电功率历史数据构造预测误差的不确定集合，集合置信度为60%。

Case 3：高置信度鲁棒模型。根据风电功率历史数据构造预测误差的不确定集合，集合置信度为70%。

Case 4：不考虑风电功率相关性的传统随机优化模型。通过对各时段风电功率预测误差概率分布采样获得用于构建场景的样本。

Case 5：计及风电功率相关性的CNC随机优化模型（本文方法）。

其中，Case 2—Case 5均考虑了不确定性，Case 2—Case 3为鲁棒优化模型，Case 4—Case 5为随机优化模型。通过对比Case 2—Case 3和Case 4—Case 5可以反映不同不确定性优化方法的性能表现差异；通过对比Case 4和Case 5则可以得到不考虑/考虑风电功率时间相关性和条件相关性的性能表现差异。

如前文所述，案例分析中使用4个月的风电数据训练鲁棒模型的不确定集合以及随机优化使用的概率分布函数和CNC模型，并用另1个月的风电数据测试各模型效果，得到的结果如图9～图10和表2所示，为1个月测试结果的平均值。

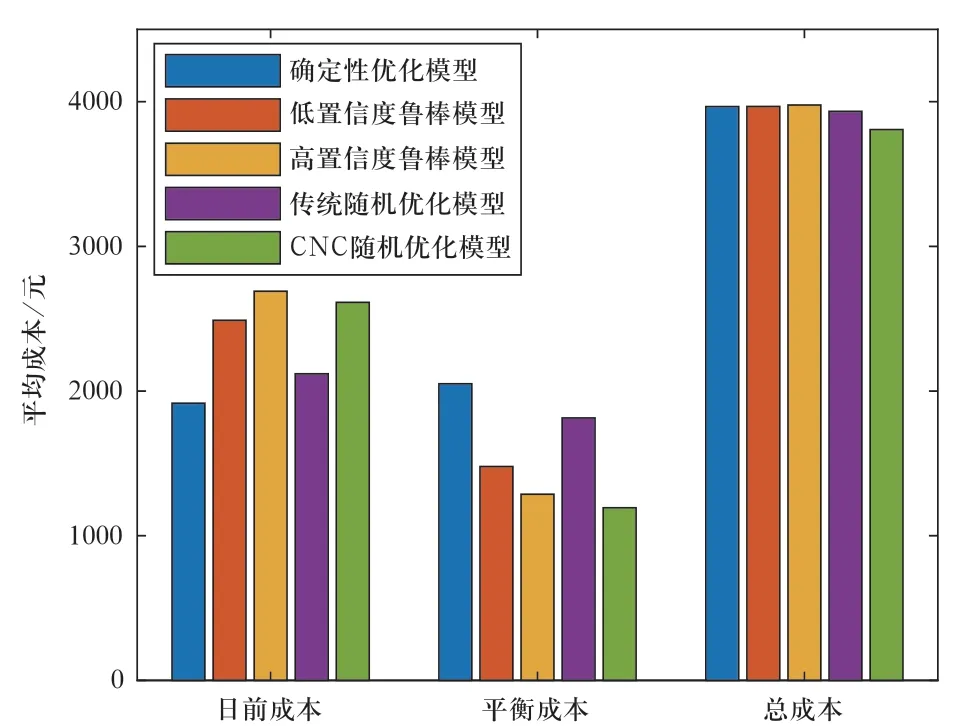
图9 不同模型的平均运行成本Fig.9 Average operation cost of different models

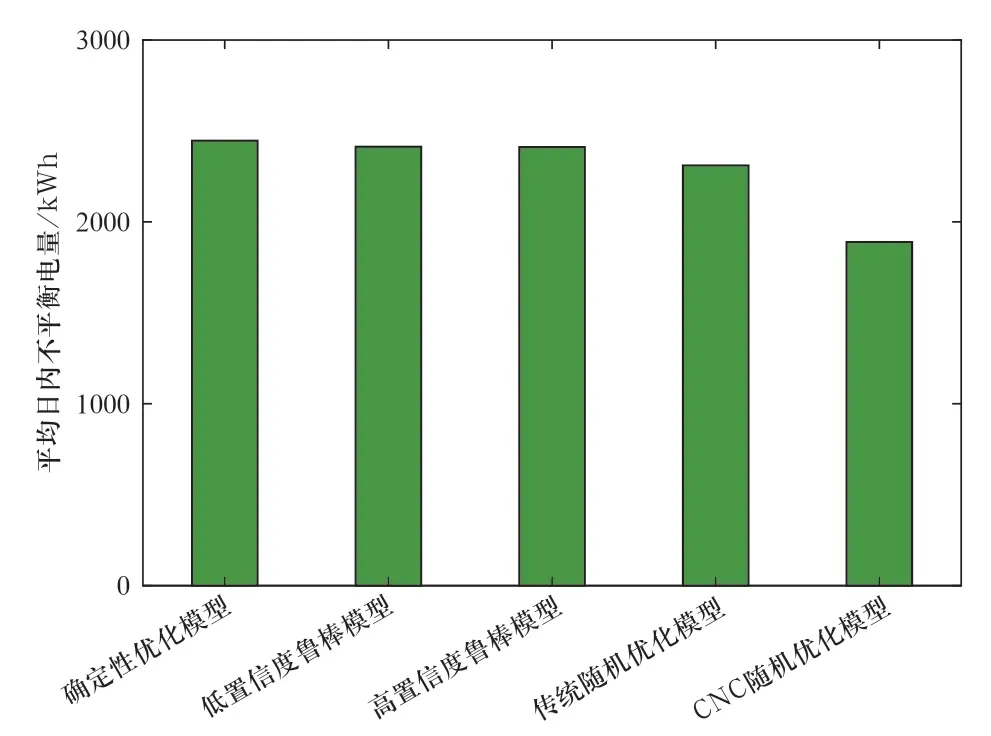
图10 不同模型的平均不平衡电量Fig.10 Average unbalanced power of different models

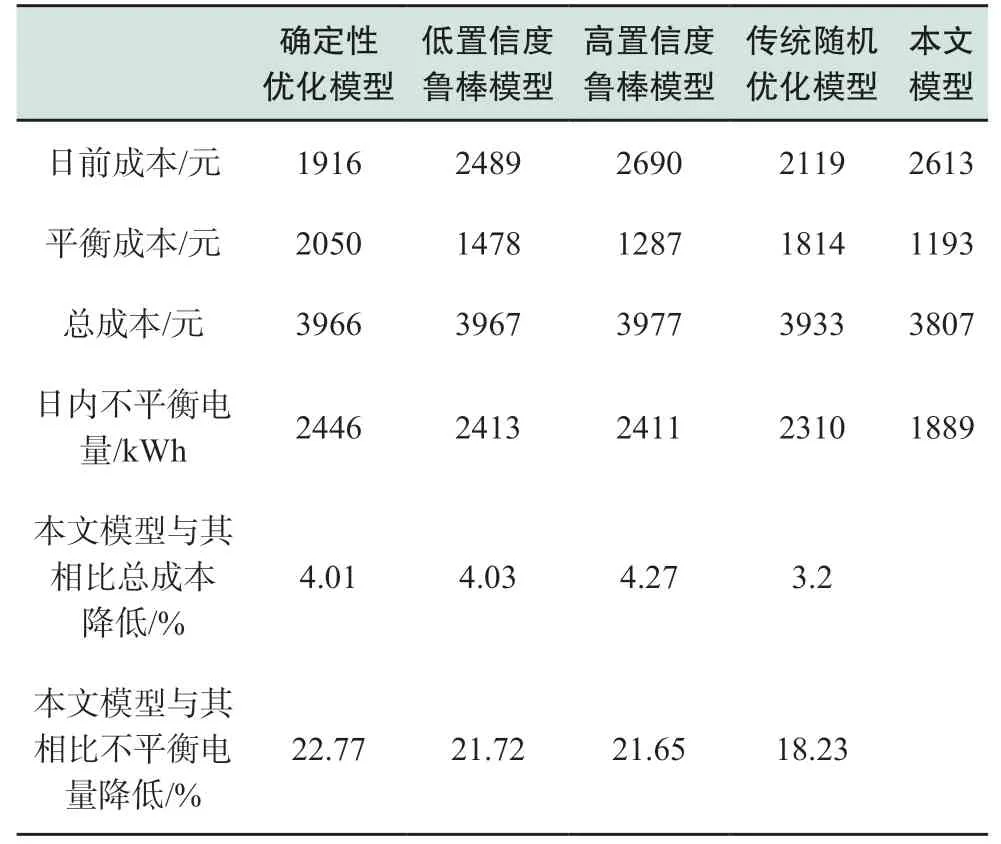
表2 不同模型的平均优化结果比较Table 2 Comparison of average optimization results of different models

图9给出了5个模型的日前成本、平衡成本以及总成本。其中，日前成本即日前优化调度模型的目标函数值，从图中看出，确定性优化模型的日前运行成本最低，因其没有考虑风电功率的不确定性，得到的调度方案是最不保守的；鲁棒优化模型和随机优化模型考虑了不确定性，因此其日前成本高于确定性模型，且鲁棒优化模型的日前成本随不确定集合置信度的增加而增加，变得更加保守。传统随机优化模型日前成本较低，保守性不强；而CNC随机优化模型的日前成本介于两个鲁棒优化模型之间，保守度较为均衡。平衡成本是微电网预测不准导致的第二日在实时市场购售电交易的成本，假定微电网在实时市场购电和售电的价格分别为日前市场的1.5倍和0.5倍。从图9中看出，由于确定性优化模型考虑的场景过于理想，日内需要购买最多的电能，因此其平衡成本是最高的；传统随机优化模型次之；相对而言，鲁棒优化模型倾向于根据不确定集合，在日前多购电/少售电，以抵抗实时市场的电价波动。CNC随机优化模型的表现则取决于实际数据的分布信息，在该算例中，随机优化模型也得到了日前多购电/少售电、日内少购电/多售电的结果，说明在该风电场的实际运行中，风电实际功率低于预测功率的场景较多。从图10看出，通过考虑风电功率的时间相关性和条件相关性，CNC模型很好地模拟出了日前预测值下风电功率的分布情况，因此根据这些场景构造的随机优化模型在日前成本低于高置信度鲁棒模型的情况下仍得到了最低的平衡功率，因此总运行成本最低。另一方面，鲁棒优化模型和传统随机优化模型没有很好地描述出风电功率的不确定场景，调度策略较为保守，因此总体效果不佳。从表2可以进一步看出，CNC随机优化模型相比确定性模型、低置信度和高置信度鲁棒模型、以及传统随机优化模型，不平衡电量分别减少了22.77%、21.72%、21.65%和18.23%，总成本分别降低了4.01%、4.03%、4.27%和3.2%，能够抵御实时市场的电价波动，得到更为合理的调度方案。

5 结论

本文分析了风电预测误差的时间相关性及其与预测值的条件相关性，并采用CNC模型对其进行建模，以日前预测值为条件，生成了计及相关性的风电功率样本，通过K-means聚类得到风电功率场景，解决了微电网随机优化问题。仿真结果表明，CNC随机优化模型能够合理调度可控分布式电源、储能、需求响应负荷等资源来最小化微电网的运行成本。该模型基于数据驱动，通过更合理的场景建模，相比于确定性模型、传统的随机模型和鲁棒模型实现了更低的总运行成本和更低的不平衡电量，因此更适用于具有一定历史数据的微电网日前调度中。在后续工作中，将重点对分布鲁棒方法和本文所提方法的性能进行对比，并分析不同样本规模下不同方法的性能表现和适用性。