评估织物悬垂性的新方法

RYKLINDzmitry РыклинДмитрийБорисович 汤晓彤

摘 要：为了开发评估织物悬垂性的新方法，建立了描述悬垂织物的数学模型，用以描述織物的悬垂外观形态，并提出了评估织物悬垂性的新指标。选取6块平纹亚麻织物，在现有的织物悬垂性能测试仪器的基础上，引入3D扫描仪，获得了悬垂织物三维图像及数据，并对所获得数据进行统计处理得出评估结果。结果表明：新开发的数学模型可以精确地描述不同亚麻织物的悬垂外观形态，通过对不同平纹亚麻织物测试和数据分析，证实了新方法具有较高的准确性，相比于伞式法，该方法可以更为有效地评估织物的悬垂形态。

关键词：悬垂性;平纹亚麻织物;3D扫描;弯曲刚度

中图分类号：TS127

文献标志码：A

文章编号：1009-265X（2022）01-0109-06

Abstract： In order to establish a new method for evaluating the drapability of fabrics， a mathematical model describing the drapability of fabrics was developed， and a new index was presented to evaluate the drapability of fabrics. Six pieces of plain linen fabrics were selected. Based on the existing testing instrument for the drapability of fabrics， a 3D scanner was introduced to obtain the 3D images and data of draping fabrics and the data obtained were statistically processed to get evaluation results. The results show that the newly developed mathematical model can accurately describe the draping appearance of different linen fabrics. The test and data analysis of different plain linen fabrics confirm that the new method has higher accuracy. Compared with the umbrella method， this method can evaluate the draping morphologies of fabrics in a more effective way.

Key words： drapability; plain linen fabric; 3D scanning; bending stiffness

悬垂性是织物的主要性能之一，该性能可以直接决定其制成产品的外观形态。从1930年开始，国内外学者们对织物悬垂性的研究一直持续至今。为了科学地判断织物的悬垂性能，其评估方法的开发也受到了各国学者的广泛关注[1-3]。悬垂性是织物在自身重量的影响下自然下垂，从而形成优美褶皱的能力[4]。从该定义可以看出，织物在悬垂状态下的外观形态及其美感程度是评估悬垂性的主要依据。

根据GB/T 23329-2009《纺织品 织物悬垂性的测定》可知，评估织物悬垂性的普遍方法是伞式法，评估指标主要为悬垂系数。该指标是取自织物在悬垂状态下形成的褶皱投影及其外轮廓线的信息，并没有考虑在悬垂状态下织物表面的整体形态。基于对科学文献的分析，可以发现，具有相同悬垂系数值的不同织物，其悬垂形态差异较大，并且它们的褶皱形状可能相同也可能是完全不同的[5]。因此，

可以说悬垂系数这一指标不足以完全评估织物的悬垂性。通过对已有文献的归纳还可以确定的是，采用3D扫描技术的研究方法是完善评估织物悬垂性方法中最有前景的方向之一，因为3D扫描仪可以提供有关悬垂织物形态的准确信息，因此各国的学者都在积极地尝试应用3D扫描技术来开发评估织物悬垂性的方法[6-9]。然而，当前已存在的评估方法尚未充分开发出表征织物悬垂形态和描述褶皱形状的复杂指标。

亚麻织物是中国的重要出口产品，在全球亚麻面料的出口份额中，中国出口量仅次于意大利。亚麻织物具有许多良好的材料性能，如高强度、高吸湿性、低过敏性和快速高温调节性能。同时，亚麻织物也有许多不足，其中最主要的性能缺点为高刚性和低悬垂性。扩展亚麻面料的应用范围、提高产品质量是提升其在国际市场竞争力的主要途径。因此，准确鉴定亚麻织物的各项性能是十分必要的。

本文选择以亚麻织物作为研究对象，重新建立数学模型及相应的评价指标来评估悬垂织物的整体外观形态，尝试对织物的悬垂性能建立一种更为有效的评估方法和评价指标。

1 理论分析及模型设定

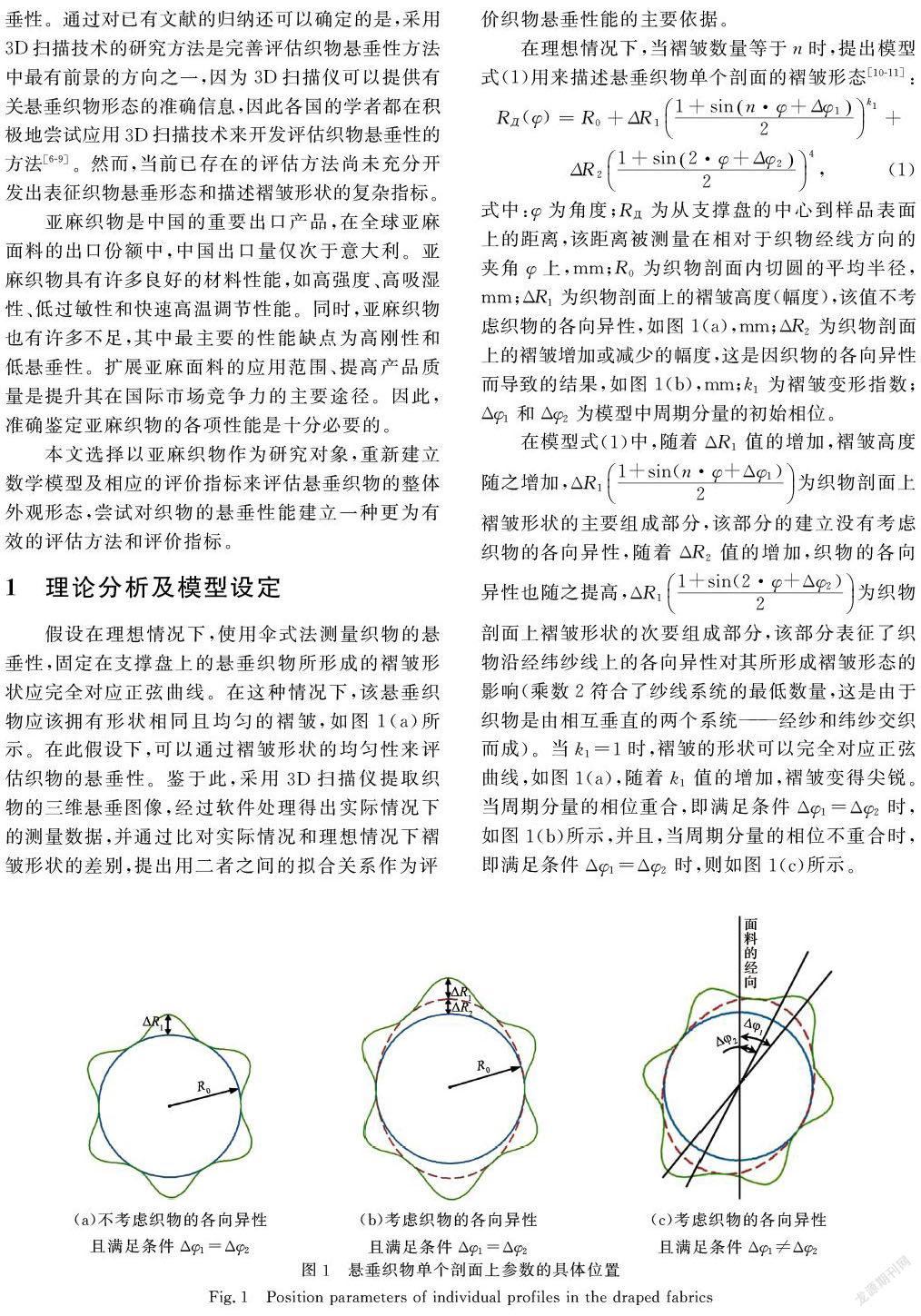
假设在理想情况下，使用伞式法测量织物的悬垂性，固定在支撑盘上的悬垂织物所形成的褶皱形状应完全对应正弦曲线。在这种情况下，该悬垂织物应该拥有形状相同且均匀的褶皱，如图1（a）所示。在此假设下，可以通过褶皱形状的均匀性来评估织物的悬垂性。鉴于此，采用3D扫描仪提取织物的三维悬垂图像，经过软件处理得出实际情况下的测量数据，并通过比对实际情况和理想情况下褶皱形状的差别，提出用二者之间的拟合关系作为评价织物悬垂性能的主要依据。

在理想情况下，当褶皱数量等于n时，提出模型式（1）用来描述悬垂织物单个剖面的褶皱形态[10-11]：

RД（φ）=R0+ΔR11+sinn·φ+Δφ12k1+

ΔR21+sin2·φ+Δφ224，（1）

式中：φ为角度;RД为从支撑盘的中心到样品表面上的距离，该距离被测量在相对于织物经线方向的夹角φ上，mm;R0为织物剖面内切圆的平均半径，mm;ΔR1为织物剖面上的褶皱高度（幅度），该值不考虑织物的各向异性，如图1（a），mm;ΔR2为织物剖面上的褶皱增加或减少的幅度，这是因织物的各向异性而导致的结果，如图1（b），mm;k1为褶皱变形指数;Δφ1和Δφ2为模型中周期分量的初始相位。

在模型式（1）中，随着ΔR1值的增加，褶皱高度随之增加，ΔR11+sin（n·φ+Δφ1）2为织物剖面上褶皱形状的主要组成部分，该部分的建立没有考虑织物的各向异性，随着ΔR2值的增加，织物的各向异性也随之提高，ΔR11+sin（2·φ+Δφ2）2为织物剖面上褶皱形状的次要组成部分，该部分表征了织物沿经纬纱线上的各向异性对其所形成褶皱形态的影响（乘数2符合了纱线系统的最低数量，这是由于织物是由相互垂直的两个系统——经纱和纬纱交织而成）。当k1=1时，褶皱的形状可以完全对应正弦曲线，如图1（a），随着k1值的增加，褶皱变得尖锐。当周期分量的相位重合，即满足条件Δφ1=Δφ2时，如图1（b）所示，并且，当周期分量的相位不重合时，即满足条件Δφ1=Δφ2时，则如图1（c）所示。

在理想情况下，当褶皱数量等于n时，悬垂织物的整体外观形态可以用模型式（2）来表示[11]：

RД（φ，H）=（a0+a1·H）+（a2+a3·H）1+sin（n·φ+Δφ1）2（a4+a5·H）+（a6+a7·H）1+sin2·φ+Δφ224，（2）

式中：H为悬垂织物表面到支撑盘的距离，mm;a0～a7为经验系数。

在模型式（1）中，经验系数a0～a7的值取决于实验测试过程的参数（如样品半径、支撑盘的半径）和测试织物的特性（如表面密度，经纬密度，经纬线刚度，编织等）。通过模型式（2），可以确定试样面料表面上每个点的位置，这主要取决于距离H和经纱方向与线段之间所构成的夹角φ。

通过数学模型式（1）的数据处理可以得出指标R21，该指标用来表征悬垂织物在距离H下的单个（一个）剖面褶皱形状的拟合程度，拟合程度越高，则剖面褶皱形状的均匀度越高。通过数学模型式（2）的数据处理可以得出指标R22，该指标用来表征悬垂织物整体形态的拟合程度，是10～25mm之间每毫米的剖面按顺序叠加起来的悬垂织物整体形态，即26个剖面褶皱形状拟合系数的平均值，拟合程度越高，悬垂织物的整体外观形态越美观。剖面褶皱形状的均匀度包涵在悬垂织物整体形态之中，所以，可以说指标R22涵盖了指标R21，但指标R22并不能完全替代指标R21。

拟合系数R21和R22的值越接近1，表示数学模型的拟合性越高，说明该悬垂织物的褶皱形状越均匀，悬垂织物的整体外观形态越美观，即织物的悬垂性也就越高，反之，则表示悬垂性差。

2 实 验

2.1 实验材料

选择6块平纹亚麻织物作为研究的对象，其规格参数见表1。表1中的悬垂系数值是按照标准GB/T 23329-2009《纺织品 织物悬垂性的测定》的公式来计算的，其评价准则应为悬垂系数值越低，则悬垂性越高。

2.2 仪器设备

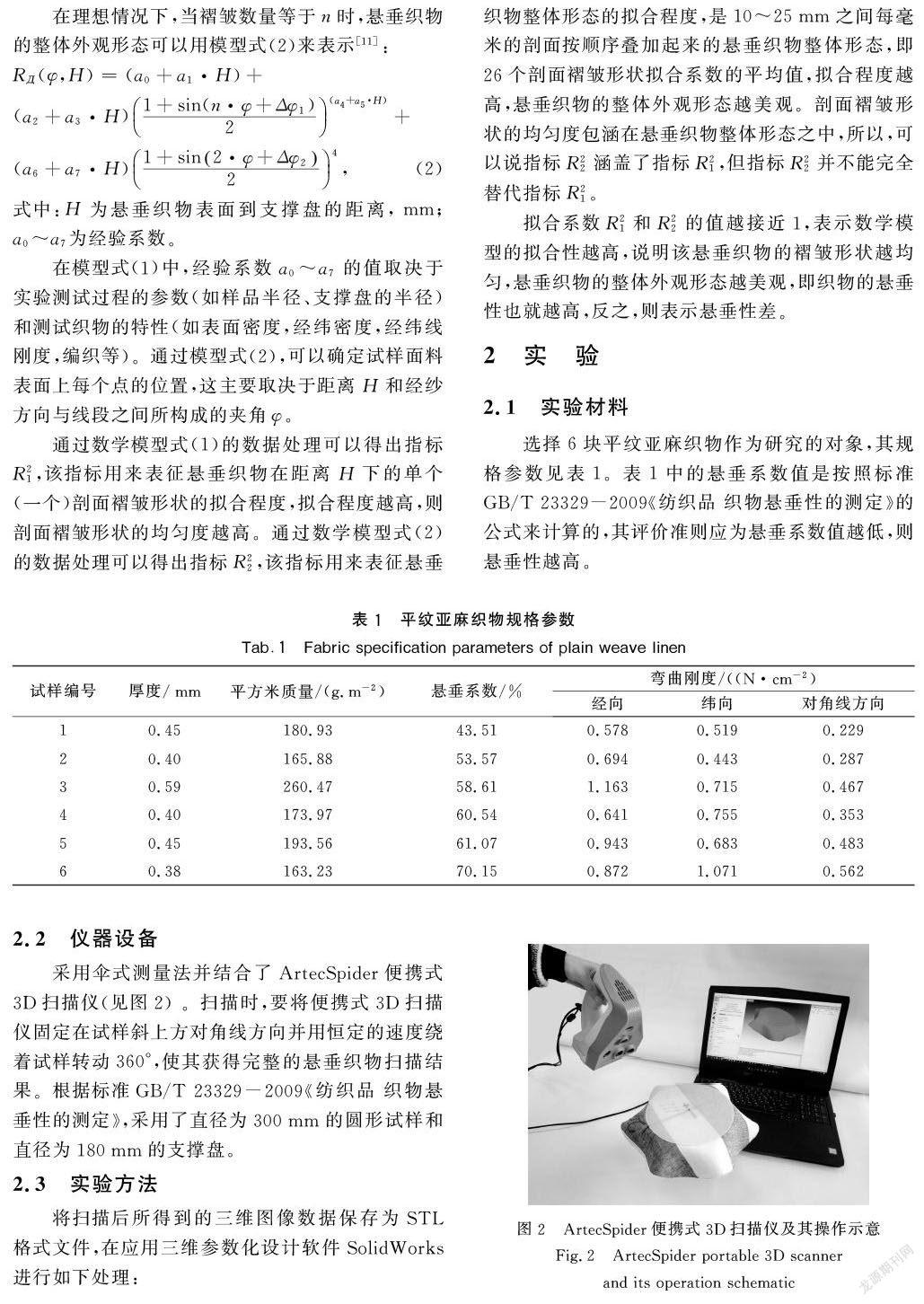
采用伞式测量法并结合了ArtecSpider便携式3D扫描仪（见图2） 。扫描时，要将便携式3D扫描仪固定在试样斜上方对角线方向并用恒定的速度绕着试样转动360°，使其获得完整的悬垂织物扫描结果。根据标准GB/T 23329-2009《纺织品 织物悬垂性的测定》，采用了直径为300mm的圆形试样和直径为180mm的支撑盘。

2.3 实验方法

将扫描后所得到的三维图像数据保存为STL格式文件，在應用三维参数化设计软件SolidWorks进行如下处理：

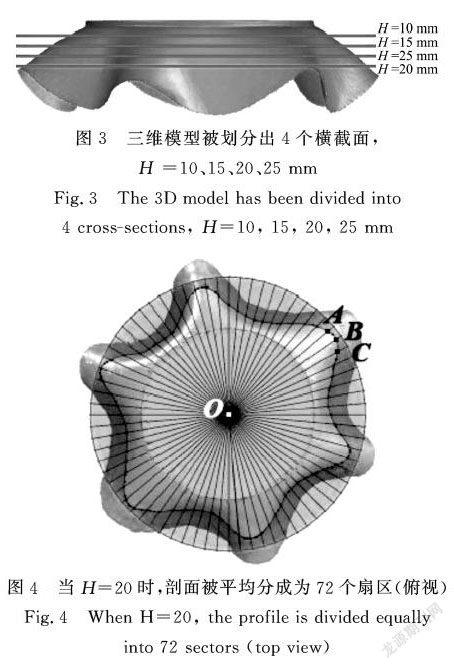
a）在获得的悬垂三维模型（正视图）上划分出4个平行截面，该截面到支撑盘的距离分别为10、15、20、25mm（图3），该距离的设定取决于试样下垂部分的高度;

b）将每个剖面平均分为72个扇形部分，每个扇形的中心角度为5（见图4）;

c）对于每个扇形部分，都要确定从支撑盘中心O点到悬垂织物表面上交汇点的距离，如A、B、C点等以此类推，所以每个截面分别要获取72个数据结果（见图4）。

3 结果与讨论

通过3D扫描仪所获取的悬垂织物表面形态的三维图像如图5所示。

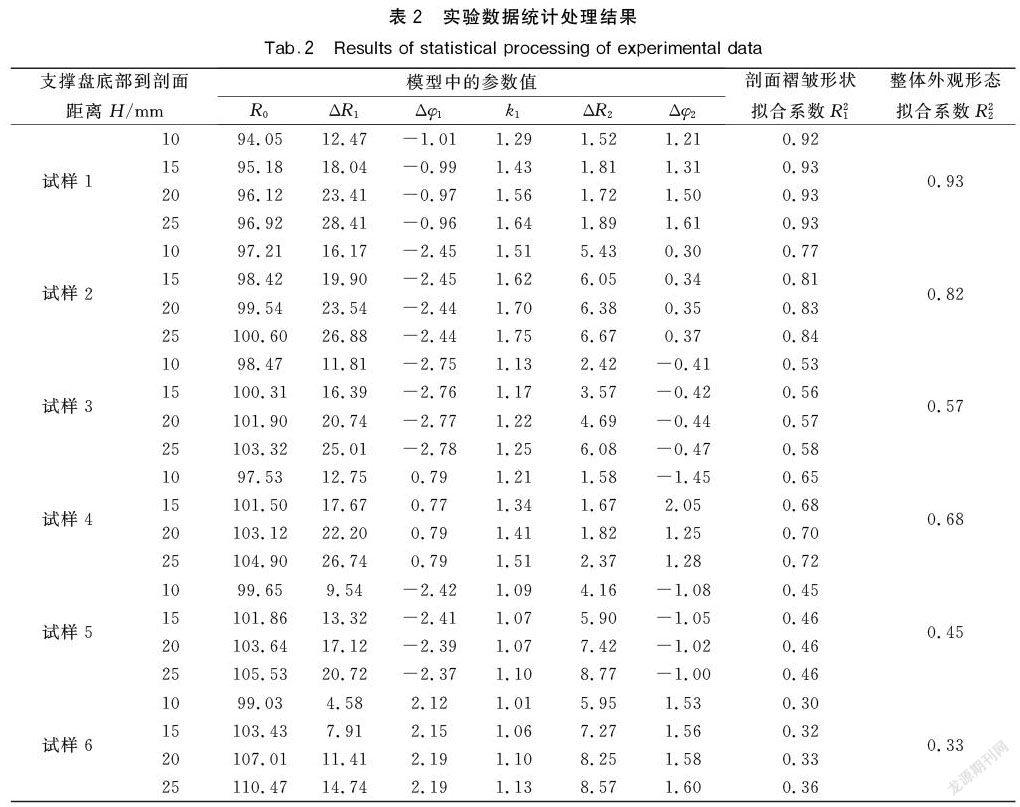
将已获取的三维扫描数据通过统计软件Statistica带入到模型式（1）和式（2）中进行拟合计算，处理结果见表2。

分析悬垂织物试样的三维图像5（a）—（f）和实验数据统计处理结果表2，可以发现：

a）剖面褶皱形状拟合系数R21的值随着支撑盘到剖面距离H的增加而提高，这表明，所测量的悬垂剖面距离支撑盘越远，其结果受支撑盘的影响就越小，试样也就越容易形成均匀的褶皱。这也说明了支撑盘到剖面距离H的值越大，其测量的准确性就越高。

b）1号试样的悬垂褶皱形状是所有图像中最均匀的，其相对应剖面褶皱形状拟合系数R21的值也比较高，在0.93～0.92之间。并且，其整体外观形态拟合系数R22的值也是最高的，为0.93，说明1号试样的悬垂性是所有试样中最好的。

c）2号试样三维图像的悬垂褶皱形状也比较均匀。系数R21的值在0.77～0.84之间，系数R22值为0.82，仅次于1号试样，这说明2号试样的悬垂性仅次于1号试样。

d）由6号试样的三维图像可以明显看出，其悬垂褶皱形状最不均匀。系数R21的值仅在0.30～0.36之间，系数R22值也是最低的，为0.33，说明6号试样悬垂性是所有试样中最差的。

e）3、4、5号试样的三维图像具有较大的差异性，3和5号试样的悬垂褶皱形状不均匀，相比它们4号试样却较为均匀。这3个试样的悬垂系数值分别为57.61，60.54 和61.07，都比较相近，很难做出明确的区分。然而，通过新方法所得到的系数R22值为：3号-0.57、4号-0.68，5号-0.45。由此可见，系数R22值可以直观地获得具有相似悬垂系数值的不同织物之间正确的悬垂性比对关系，并且该指标的比对结果完全符合直观的三维图像结果。

f）在排除2号试样的情况下，所有试样的ΔR2值都是随着系数R21值的增加而降低，也就是说，剖面褶皱形状的均匀度随着织物各向异性的增加而下降。并且，在对比织物规格参数和实验数据统计处理结果时，发现，随着织物对角线方向（45°）上弯曲刚度的降低其系数R22的值也在提高。在徐军等[12]的文章中也有类似的发现，他们认为织物在弯曲时存在明显的各向异性，且织物在对角线方向（45°）上的弯曲刚度是最小的，因此可以说它对褶皱形成的影响是最大的。导致2号试样的各向异性值比较高的原因可能是由于该织物经纬向上的弯曲刚度的差异略大。

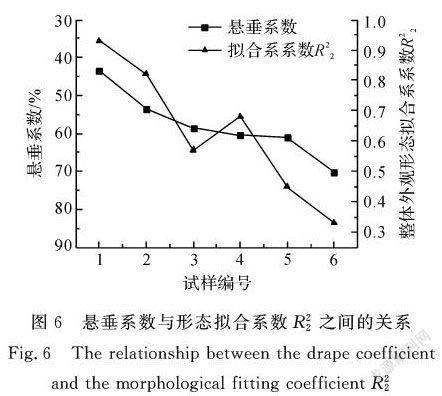
图6为悬垂系数与整体外观形态拟合系数R22的变化趋势关系。由图6可知，这两种系数的指标结果其整体变化趋势基本一致。1号试样悬垂系数最低，系数R22值最高，而6号试样的悬垂系数最高，系数R22值也最低，这说明该指标的评价结果具有较高的可行性。尽管，4号试样和5号试样的悬垂系数结果非常相近，但4号试样的整体外观形态拟合系数R22值却明显高于3号试样。对比织物的三维图像，也可以发现相同的评价结果。与伞式法相比，新方法的测量结果更加符合三维图像的直接观测结果，尤其是当不同试样之间的悬垂系数值较为接近时。

4 结 论

不同的亚麻织物所得到的褶皱形态剖面拟合系数R21和整体外观形态拟合系数R22的结果符合其三维图像的对应关系。这证实了，新方法所提出的数学模型可以正确描述不同亚麻平纹织物的悬垂外观形态。

因此，可以确定的是，评估悬垂性的新方法具有较高的准确性。与伞式方法相比，在织物悬垂性差异较小的情况下或者是当织物所测得的悬垂系数结果较为接近时，新方法可以更为有效地评价织物的悬垂性。除此之外，从数学模型式（1）和式（2）中还获得了其他的参数指标，这些参数指标还有待进一步研究和验证。

参考文献：

[1]SANAD R， CASSIDY T， VIEN C， Evans E. Fabric and garment drape measurement Part 2[J]. Journal of Fiber Bioengineering and Informatics， 2013， 6（1）： 1-22.

[2]TSAI K H， TSAI M C， WANG P N， et al. New approach to directly acquiringe the drape contours of various fabrics[J]. Fibres & Textiles in Eastern Europe， 2009， 17（3）： 54-59.

[3]GNANAVEL P， ANANTHAKRISHNAN T. Volume based measurement of fabric drape using surfer software and studies on effect of influencing factors[J]. Journal of Textile Science & Engineering， 2014， 4（4）： 159.

[4]姚穆.纺织材料学[M].北京：中国纺织出版社，1980：383.

YAO Mu.Textile Materials[M]. Beijing： China Textiles Press， 1980： 383.

[5]CARRERA-GALLISSà E， CAPDEVILA X， VALL-DEPERAS J. Evaluating drape shape in woven fabrics[J]. Journal of the Textile Institute， 2017， 108（3）： 325-336.

[6]GLOMBIKOVA V， KUS Z. Drape evaluation by the 3D drape scanner[J]. Tekstil ve konfeksiyon， 2014， 24（3）： 279-285.

[7]沈偉，任静，周华，等.基于Kinect传感器的织物悬垂性测试[J].2014，31（5）：306-309，328.

SHEN Wei， REN Jing， ZHOU Hua， et al. Fabric drape measurement method based on kinect sensor[J]. Journal of Zhejiang Sci-Tech University， 2014， 31（5）： 306-309， 328.

[8]张晓婷，洪剑寒，查神爱，等.基于三维扫描技术的毛织物悬垂性能测试方法[J].毛纺科技，2015，43（10）：58-61.

ZHANG Xiaoting， HONG Jianhan， ZHA Shen'ai， et al. Study on the drape performance testing method of wool fabric with three-dimensional scanner[J]. Wool Textile Journal， 2015， 43（10）： 58-61.

[9]YU Z C， ZHONG Y Q， GONG R H， et al. New indicators on fabric drape evaluation based on three-dimensional model[J]. Textile Research Journal， 2020， 90（11/12）： 1291-1300.

[10]РЫКЛИН Д Б， ТАН С， ГРИШАЕВ А Н， ПЕСКОВСКИЙ Д В. Разработка математической модели драпированной ткани с использованием данных， получаемых в процессе 3D-сканирования[J]. Вестник Витебского государственного технологического университета， 2018， 1（34）： 70-78.

RYKLIN D B， TANG X， GRISHAEV A， et al. Development of mathematical model of draped fabric with use of 3-d scanning data[J]. Vestnik of Vitebsk State Technological University， 2018， 1（34）： 70-78.

[11]РЫКЛИН Д Б， ТАН С. Оценка анизотропии драпируемости тканей на основе анализа результатов 3D-сканирования[J]. Известия высших учебных заведений. Технология текстильной промышленности， 2020， 2（386）： 137-145.

RYKLIN D B， TANG Х. Evaluation of fabrics dreapeability anisotropy on the base of 3d-scanning results analysis[J]. Higher Education Institutions Textile Industry Technology， 2020， 2（386）： 137-145.

[12]徐軍，姚穆.织物弯曲刚度各向异性探讨[J].西北纺织工学院学报，2001，15（2）：102-104，135.

XU Jun， YAO Mu. Discussion on bending rigidity anisotropy of fabrics[J]. Journal of Northwest Institute of Textile Science and Technology， 2001， 15（2）： 102-104， 135.