横流环境下振荡射流初始稀释规律
2022-02-13徐振山黄振超陈永平张长宽
徐振山,黄振超,李 蒙,陈永平,张长宽
(河海大学港口海岸与近海工程学院,江苏 南京 210098)
射流在达标废水排放、火/核电厂温排水、海水淡化厂浓盐水排放等方面具有广泛应用,其运动和稀释规律一直是河流海岸水动力-水环境研究关注的重点问题。对于如何提高射流中污染物质(营养盐、热量、盐等)在受纳水体中的稀释度以降低对周围生态环境的影响是近年来的研究热点[1-3],相关研究可提高对射流运动和稀释规律的认识,并为排放工程设计提供参考。
射流在横流环境下的运动和稀释规律研究成果较为丰富。学者们开展了大量物理试验和数值模拟研究,详细分析了影响横流环境下射流稀释度的关键因素。姜国强等[4]发现由于2种流体间的相互作用,射流背流面形成了绕流分离旋涡,其结构与射流喷口形式和射流-横流流速比有关;射流-横流速度比是描述射流流动和稀释特性的最关键参数[5-6],其比值越大,射流扩散范围越大,射流偏转越弱;Moawad等[7]对不同射流-横流速度比下射流浓度场进行了测量,得到了射流最小稀释度的经验公式;Roberts等[8]对横流环境下的倾斜射流进行了研究,发现雷诺数小于25时初始流量的影响可以忽略,射流稀释度随射流与横流夹角的增大而提高;Lai等[9]发现在受纳水体确定的前提下,排放工程可通过采用多孔或玫瑰型扩散器,即调整排放口形状或排放角度,达到提高初始稀释的目的。2011年以来,国内学者逐步开展了波浪对横流环境下射流稀释规律的影响研究。波浪时间尺度与射流相当,水质点摆动有利于污染物的扩散和稀释[10]。波浪的存在增大了环境流场的速度变化程度,射流在波流共同作用下将出现污染物云团现象,稀释度明显提高。Xu等[11-13]、徐振山等[14]通过大涡模型研究了射流在波流环境下的三维运动和稀释特性,得到了波流环境下射流稀释能力的一系列经验公式;同时,Xia等[15]研究了周期性水流运动对射流运动规律的影响,发现了类似于波浪的效果。
总体来看,现有研究主要集中在射流口布置型式和受纳水体对稀释效果的探讨上,尚未开展射流排放流量动态变化对稀释的影响,振荡射流(即流量随时间动态正弦变化)对射流稀释的具体影响也不得而知。李蒙等[16]建立了横流环境下振荡射流的三维大涡数学模型,并初步分析了横流环境下振荡射流的运动规律。本文将在此基础上进一步研究射流振荡参数对射流稀释规律的影响。
1 研究方法
1.1 横流环境下振荡射流数学模型
横流环境下振荡射流大涡模型控制方程为空间平均的Navier-Stokes(N-S)方程和浓度标量输运方程。垂向上,模型引入σ坐标解决自由面追踪问题。数值方法采用算子分裂法,将模型求解分为对流项、扩散项和压力传播项3步。采用二次向后特征线法和Lax-Wendroff格式平均法对对流项进行离散求解,采用时间前差、空间中心差分格式离散求解扩散项,利用共轭梯度算法求解泊松方程。
横流速度入口边界遵循对数型流速垂线分布,压力条件遵循吕升奇等[17]的物理试验结果,横流出口边界采用零梯度条件。振荡射流的出口紊动采用合成涡方法[18]生成,以满足紊动速度各分量的随机性要求。侧向边界采用不可入边界条件,即各物理量壁面法向分量为0。采用拉格朗日-欧拉法追踪自由表面。
模型计算域长9.0 m,宽0.5 m,高0.5 m,在距离入流边界4.0 m处布置振荡射流,振荡射流管径为1.0 cm。坐标原点位于射流出口中心处,x、y、z分别为长度、宽度和高度方向坐标。为验证数学模型的合理性和准确性,以静水环境下非振荡射流、静水环境下振荡射流和横流环境下非振荡射流的物理试验数据与模型结果进行对比验证。关于横流环境下振荡射流数学模型的更多介绍和验证结果可参见相关文献[1,16]。
1.2 横流环境下振荡射流量纲分析
影响横流环境下振荡射流稀释的因素有2类:一是射流本身的参数,即管径(d)、平均速度(w0)、初始浓度(c0)、射流振荡周期(T)以及振幅(wA);二是背景流场参数,即横流速度(u0)。上述参数是影响射流稀释特性的最基本参数。对以上参数进行组合,得到影响射流稀释特性的量纲一特征参数,如射流-横流速度比(Rjc)是描述射流流动和混合特性的关键参数;振幅-射流速度比(Raj)可以体现振荡幅度的影响;斯特劳哈尔数(St)体现振荡周期对稀释程度的影响。3个量纲一参数的公式如下:
(1)
(2)
(3)
横流环境下非振荡射流的组合特征参数主要有射流初始动量、特征长度等,可采用类似组合特征参数对振荡射流稀释规律进行分析。考虑到射流的振荡性,振荡射流的特征速度(wch)定义如下:
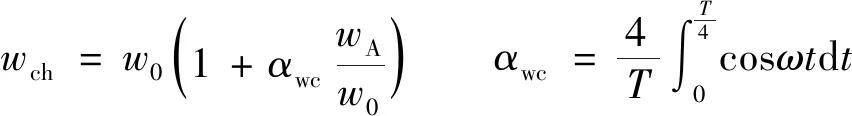
(4)
式中:ω为射流的振荡频率,即ω=2π/T;αwc表征振荡速度对特征速度的贡献程度,通过积分计算可得αwc=0.637。振荡射流的特征动量(Mch)为
(5)
横流环境下振荡射流的特征长度(Lm)为
(6)
特征长度的物理含义是振荡射流与横流的相对强弱,振荡射流稀释规律主要受Lm影响。
1.3 模拟工况设置
为探究量纲一参数对横流环境下振荡射流的影响,设置了10组数值试验,各组次参数如表1所示。振荡射流的初始质量浓度均为0.15 mg/L。试验设计中,分别考虑不同的振荡振幅和振荡周期,探究Raj和St对横流环境下振荡射流运动和稀释特性的影响。
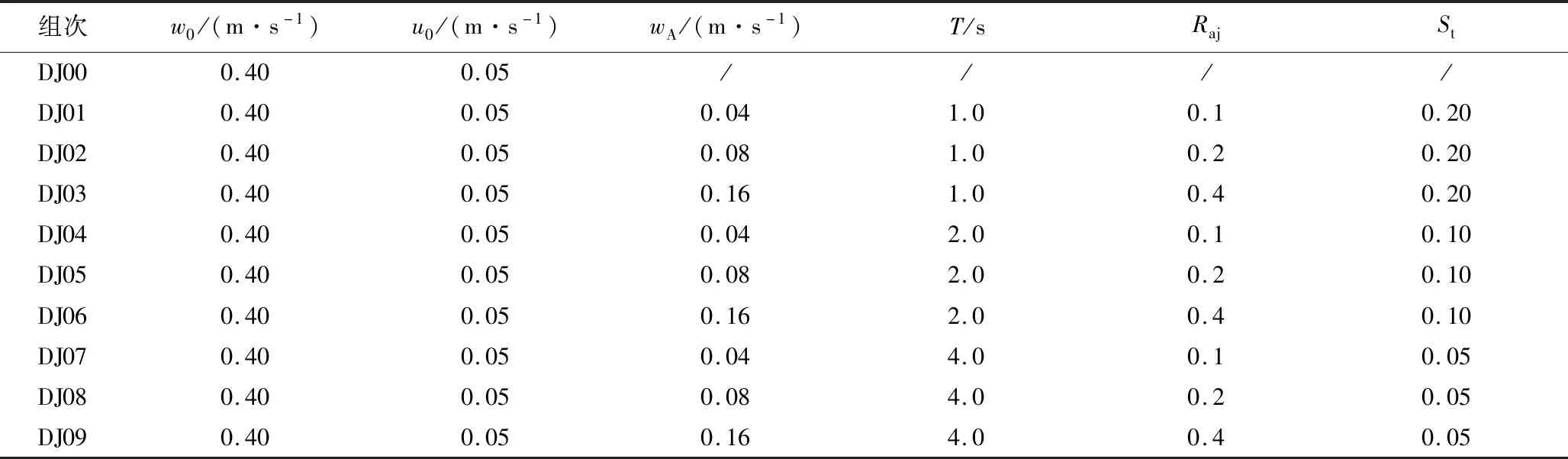
表1 横流环境下振荡射流计算组次及参数Table 1Numerical cases and parameters of oscillating jet in cross-flow environment
2 结果与讨论
2.1 横流环境下振荡射流运动规律
图1为组次DJ05 4个典型相位下对称纵剖面上射流相位平均速度场与质量浓度(c)场。在周期性振荡作用下,射流体出现了明显的间歇性“污染物云团”现象,与波流共同作用下射流的形态特征极为类似[11],A1—B1—C1—D1—A2代表“污染物云团”在1个振荡周期内形成和发展的过程。与横流环境下非振荡射流相比,“污染物云团”使得振荡射流与周围水体的掺混面积大大增加,二者相互作用显著增强。

图1 组次DJ05典型相位下对称纵剖面上射流相位平均流场和质量浓度场Fig.1 Phase-averaged flow field and concentration field on symmetrical plane under typical wave phases of case DJ05
图2为组次DJ00、组次DJ04—DJ06不同下游断面上射流的时均质量浓度分布。由于反向对称漩涡(CVP)结构的存在,横流环境下非振荡射流的下游断面时均质量浓度出现2个极大值[14]。在周期性振荡作用下,下游断面时均质量浓度分布发生了一定变化。根据振荡强度的不同,下游断面时均质量浓度可能出现CVP结构引起的2个极大值(组次DJ04),也可能出现由于“污染物云团”引起的1个极大值(组次DJ06)。组次DJ04中,下游断面上时均质量浓度的最大值都发生在射流体下部CVP结构的涡心位置。组次DJ06中,下游断面上时均质量浓度的最大值发生在“污染物云团”的位置。组次DJ06中,随着射流体向下游行进,由于“污染物云团”引起的质量浓度极大值逐渐演变为2个质量浓度极大值,可以认为“污染物云团”的位置又逐渐演变出了新的CVP结构。

图2 横流环境下振荡射流下游断面上时均质量浓度分布Fig.2 Time-averaged concentration distribution on downstream sections of oscillating jet in cross-flow environment
2.2 各量纲一参数对射流稀释规律的影响
Lee等[19]建议采用断面浓度最大值(Cm)(或断面最小稀释度(Sc))、断面浓度最大值的垂向位置(Zm)、宽度(Rh)和高度(Rv)来描述横流环境下射流下游断面上的浓度特征,如图3(a)所示。本研究采用类似的指标对横流环境下振荡射流下游断面上的浓度特征进行分析。与Lee等[19]不同的是,本研究采用由0.25Cm等值线决定的断面可视范围面积代表上述的Rh和Rv(以下称为射流可视范围面积A25%),如图3(b)所示。

图3 特征稀释参数示意Fig.3 Characteristic dilution parameter definition
据2.1节分析可知,Zm因射流振荡幅度的不同可能出现在射流体下部CVP结构的涡心位置或射流体上部的“污染物云团”位置,故不针对其开展讨论。以下主要分析射流振荡幅度和射流振荡周期对Sc和A25%的影响。选取组次DJ04—DJ06和组次DJ02、DJ05、DJ08进行比较,如图4和图5所示。DJ04—DJ06组次的Raj依次为0.1、0.2和0.4,St与Rjc均相同。由图4分析可知,Raj越大,Sc和A25%越大。以Sc为例,在x/d=20断面上,4组的数值分别为22、25、35和40。可见,随着Raj增加,射流体与周围水体掺混加剧,射流的扩散范围与稀释能力得到显著提高。图5为St影响下横流环境下振荡射流各稀释参数对比,2组的Raj与Rjc相同。组次DJ02、DJ05和DJ08的St依次为0.20、0.10和0.05。随着St的减小,A25%增加,而Sc变化不明显。
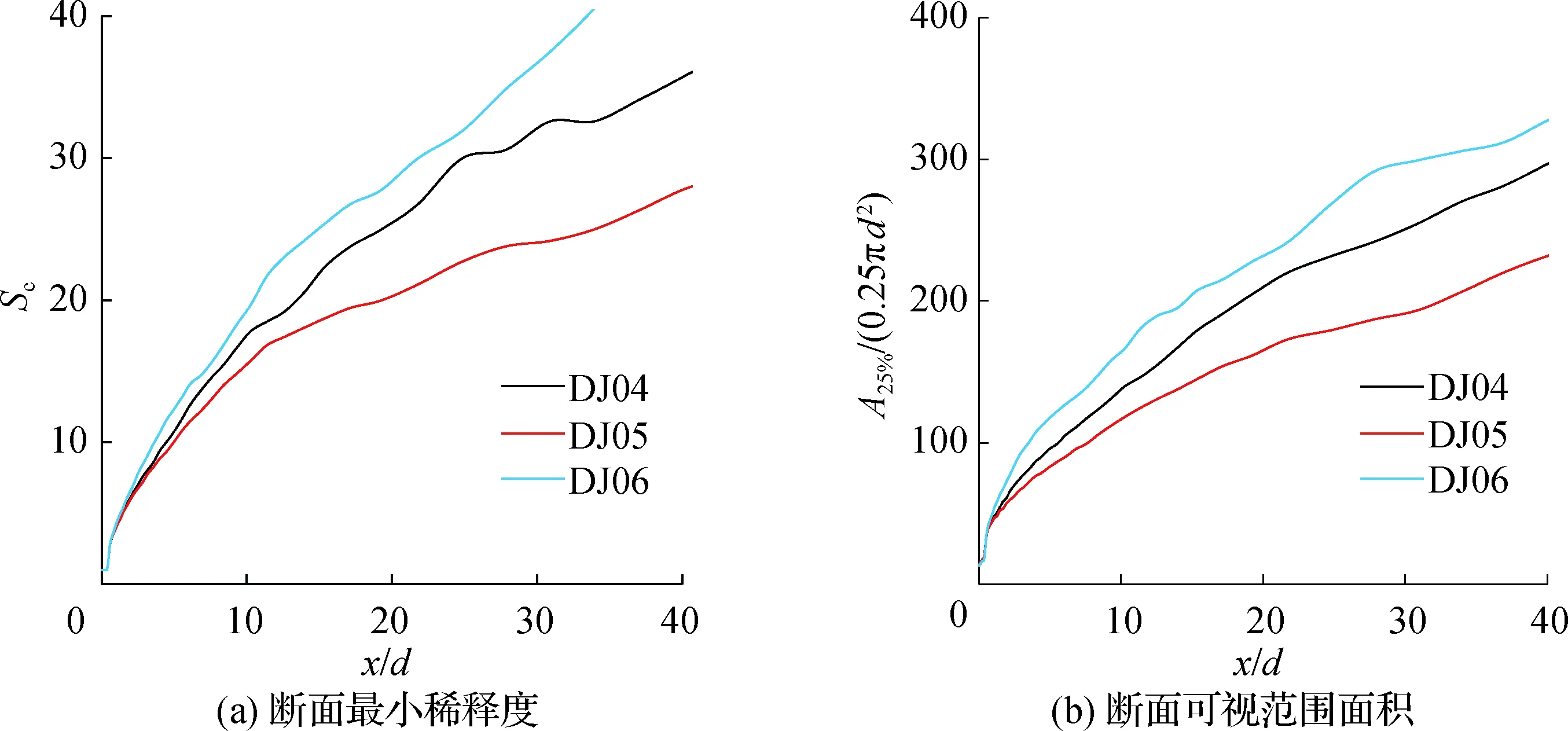
图4 振幅影响下横流环境下振荡射流各稀释参数对比Fig.4 Comparison of dilution parameters of oscillating jet in cross-flow environment under the influence of amplitude

图5 斯特劳哈尔数影响下横流环境下振荡射流各稀释参数对比Fig.5 Comparison of dilution parameters of oscillating jet in cross-flow environment under Strouhal number effect
2.3 横流环境下振荡射流初始稀释经验公式
在以往研究中,对于横流环境下非振荡射流,通常仅对下游对称纵剖面(y/d=0)的最小稀释度(Sc0)进行曲线拟合[19]。类似波流环境下非振荡射流经验公式[13],本文对Sc及A25%进行曲线拟合,分别计算各组次的wch、Mch、Lm及St,结果如表2所示。

表2 横流环境下振荡射流特征参数Table 2Characteristic parameters of oscillating jet in cross-flow environment
利用上述特征参数对断面最小稀释度和断面可视范围面积进行量纲一化,如图6所示,得到二者的经验公式分别如下:
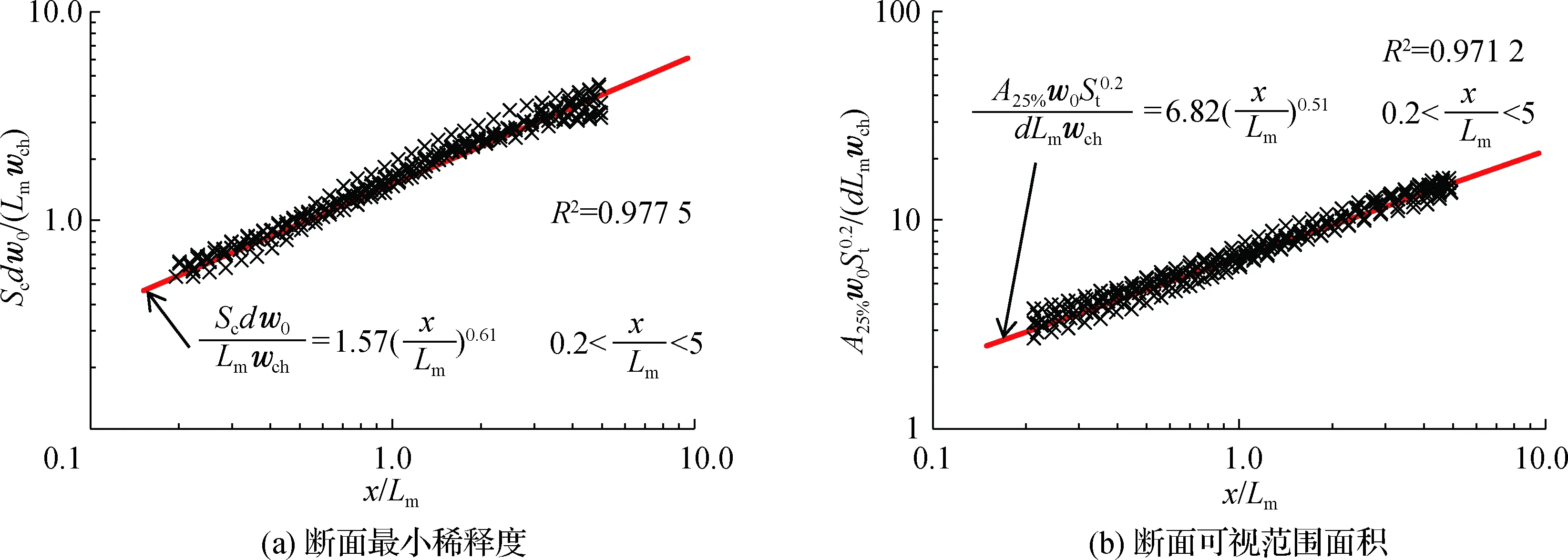
图6 横流环境下振荡射流的断面最小稀释度公式和断面最小可视范围面积公式Fig.6 Formula for the minimum dilution and the visible area of oscillating jet in cross-flow environment
(7)
(8)
整体来看,Lm和wch的组合能够较好地表征振荡射流断面最小稀释度的沿程变化规律,而Lm、wch以及St的组合能够较好地表征振荡射流断面可视范围面积的沿程变化规律。实际上,波流环境下的非振荡射流与横流环境下的振荡射流运动形态较为相似,比如“污染物云团”现象,波浪的振荡作用和射流的振荡作用是“污染物云团”现象出现的重要原因,振荡作用使得射流水体与受纳水体的掺混更加剧烈,对射流的初始稀释具有一定促进作用。
表3列出了横流环境下非振荡射流、波流环境下非振荡射流和横流环境下振荡射流初始稀释规律的经验公式。从断面最小稀释度拟合公式的对比中可以看出,各个公式结构基本一致,区别仅在于是否考虑波浪的影响(uch/u0,uch为波浪特征速度)和振荡作用的影响(wch/w0)。如去除波浪与振荡作用的影响,三者公式的结构均为Scd/Lm=C1(x/Lm)C2(C1、C2为系数)。波流环境下非振荡射流和横流环境下振荡射流断面最小稀释度拟合公式的不同之处在于,公式左侧分别是u0/uch的平方和w0/wch的一次方。将式(6)代入式(7)和式(8),将Lm转换成w0/wch,得到式(9)和式(10)。波流环境下非振荡射流同理得到式(11)和式(12)。由此可见,断面最小稀释度分别与uch的1.58次方和wch的1.39次方成正比,在数值上相近。对比断面可视范围面积公式,波流环境下非振荡射流与横流环境下振荡射流的公式结构类似。通过将2个公式的对比分析,在波流环境下非振荡射流和横流环境下振荡射流断面可视范围面积均与St的0.2次方成反比,分别与uch的1.42次方和wch的1.49次方成正比,这也表明在最小稀释度上,振荡射流产生的作用与波浪类似。

表3 浓度特征指标公式结果汇总Table 3Summary of the results of the concentration characteristic index formulas
(9)
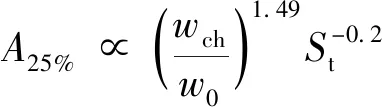
(10)
(11)
(12)
3 结 论
本文利用三维大涡数学模型研究了横流环境下振荡射流的振荡参数对射流稀释规律的影响,得到以下结论:
(1) 振幅-射流速度比越大,横流环境下振荡射流最小稀释度和断面可视范围面积越大;随着斯特劳哈尔数的减小,断面可视范围面积增加,而最小稀释度变化不明显。
(2) 在引入射流特征速度与特征长度的基础上,通过量纲分析,得到了横流环境下振荡射流断面最小稀释度以及断面可视范围面积的经验公式。
(3) 横流环境下振荡射流与波流环境下非振荡射流初始稀释经验公式在结构上类似,表征波浪的参数(uch/u0)和振荡作用的参数(wch/w0)对射流初始稀释规律的影响较为接近。
