探究辅助角公式中“φ”的确定与运用
2022-02-13黄文青
中学生数理化·高一版 2022年1期
■黄文青
在三角函数中,有一种常见而重要的题型,即化asinx+bcosx为一个角的三角函数形式,进而求原函数的周期、值域、单调区间等。这就要求同学们需要记忆和掌握辅助角公式。
一、辅助角公式中“φ”的确定方法
asinx+bcosx=(sinxcosφ+cosxsinφ)=,其中tanφ=,φ所在的象限由系数a,b的符号确定。一般地,由tanφ0=求出锐角φ0,若点(a,b)在第一象限,则取φ=φ0;若点(a,b)在第二象限,则取φ=π-φ0;若点(a,b)在第三象限,则取φ=π+φ0;若点(a,b)在第四象限,则取φ=-φ0。这样处理辅助公式中的“φ”的值,既不容易出错又简单易学。

评析:在寻找角的过程中,一定要找“同一个角”的正弦值和余弦值。
练习1:函数f(x)=2sinxcosx-的最小正周期是____。
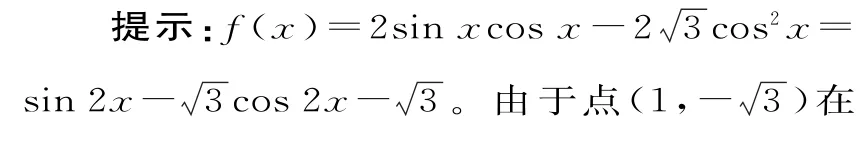

二、辅助角公式中“φ”的运用
对于辅助角“φ”,一方面要注重研究其来源,另一方面要把握辅助角与原生角的范围关系,确定其大致范围,可以更好地掌握和使用公式。
例2当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ=____。

评析:解答本题的关键是利用正弦函数的性质寻求辅助角与原生角的范围关系。
练习2:已知,则tanα的值为____。

