冻融循环作用下砂土粒组变化的分形特征及其与长期强度的相关性分析

刘 启， 张 泽，3， 张圣嵘， 恽晴飞， 付峻松

（1.东北林业大学 土木工程学院/寒区科学与工程研究院/冻土研究所，黑龙江 哈尔滨 150040；2.东北林业大学 东北多年冻土区地质环境系统教育部野外科学观测研究站/东北多年冻土区环境、道路建设与养护协同创新中心，黑龙江 哈尔滨 150040；3.中国科学院 西北生态环境资源研究院 冻土工程国家重点实验室，甘肃 兰州 730000；4.上海长凯岩土工程有限公司，上海 200093）

0 引言

冻土是指温度在0 ℃及以下，并含有冰的各种岩石和土壤［1］。根据存在时间，地球上主要分布两类冻土，即多年冻土和季节冻土。在我国，多年冻土主要分布在青藏高原、祁连山以及东北等地区［2］。季节冻土在我国分布更加广泛，季节冻土区由于受到四季交替，冷暖变化引起的反复冻融作用，路基会出现冻胀、沉陷等一系列灾害。可以将冻融循环理解为一种特殊的强风化作用［3］，导致土体物理力学性质均在不同程度上发生改变。大量学者研究发现冻融循环作用会改变土体结构［4-5］、模量［6］、孔隙率［7］等与土体长期强度密切相关的因素。因此在受冻融作用影响的地区建设工程设施时，尤其有必要考虑土体的长期强度变化规律问题［8-9］。

Mandelbrot［10］提出了分形的概念，分形理论的出现为研究分布复杂且无规则的事物提供了一个有力的工具。已有大量学者证明岩石和土体具有良好的分形特性［11-14］。以往的学者针对各类土体进行了研究，取得了一些规律性的成果。例如，Li等［14］通过对钙质砂表面分维以及质量分维的研究发现，对于颗粒破碎的定量描述，分形维数比形状描述符更具有统计规律性。陈鑫等［15］基于不同的分形模型，利用压汞法，定量分析了冻融循环对黄土孔隙的改变规律。于钱米［16］通过建立增长路径法（GP），推导出粗粒土颗粒破碎的极限二维分形模型和极限分形维数，并计算了粗粒土的极限分形维数约为2.585。王展等［17］使用人工控温冻融的方法，从冻融次数和分形维数入手，揭示了冻融循环对土微团聚体稳定性改变的影响机制。周泓等［18］则借助球形模板压入仪探究了冻融循环作用对黄土长期强度的劣化机制。刘建坤等［19］通过不固结不排水剪切试验，研究了冻融作用下细粒土的不均匀分布对粗粒土力学特性的影响。张泽等［20］通过对冰碛亚黏土的反复融冻试验，发现粒度成分呈双向性变化，大颗粒发生分裂，小颗粒发生团聚，粒径呈现均一化发展。卜建清等［21］通过室内三轴试验研究，发现在经历冻融循环后，细粒土的冻胀削弱了粗粒土的强度，并建议以6 次冻融循环后的力学指标作为参考值。

综上所述，在已有的成果中很少涉及土体在经历冻融循环作用后，内部的粒组与长期强度的变化规律。因此本文以冻结砂土为研究对象，使用球形模板压入仪获得了不同冻融循环次数下冻结砂土的长期强度，利用分形理论和显著性分析的方法，探究冻结砂土的不同粒组与长期强度的变化趋势，以期得到不同冻融次数下粒度含量对冻结砂土长期强度的影响规律。

1 试验方法

1.1 试样制备

本文以两种不同粒度范围的砂土为研究对象，如图1 所示的试验方案设计图，其中C 代表冻融循环，例如C4 表示样品经历了4 次冻融循环。试样进行指定次数的冻融循环试验后进行球形模板压入试验。

图1 试验方案Fig.1 The test scheme

根据《公路土工试验规程》（JTG E40—2007）的制备要求，参与试验的砂土均过2 mm 筛，颗粒级配曲线如图2所示，并依据该规程以及叙述简便，将土样相对粒度范围较小的称为细砂（FS），反之则称为中砂（MS）。试验土样的干密度为2.65×103kg·m-3，均为饱水状态。标准环刀和样品的底面内径为61.8 mm，高为20.0 mm。样品采用制样机制备，试样制备完成后，放入饱和缸内进行抽真空饱和，同时用保鲜膜与宽胶带进行保存密封。试验样品的冻结、融化温度分别为-20 ℃与20 ℃，在冻融循环箱中进行样品的冻融，冻融过程无外界水源补给。样品采用多向冻融，即从试样外围向中心冻结。试验进行前，在所设定的冻结和融化温度下，对单个样品进行了反复的冻结和融化试验，发现当冻结和融化时间设置为2 h 时，试样均能完成充分的冻结和融化，因此将样品的冻结与融化时间均设置为2 h。为模拟季节冻土区的冻融作用对土体的影响，将冻融循环次数N设为4、6、10、50、100 次，对达到要求的冻融样品进行球形模板压入试验。其中冻土强度降低最急剧的阶段是在加载初期，加载8 h得到的黏聚力仅为超极限长期黏聚力的0.10～0.35倍，加载16 h 后冻土的黏聚力已不再发生变化，此时的黏聚力便可视为冻土的长期黏聚力［22］。所以为了实用，极限长期黏聚力可近似地根据短期的，例如8 h 后的试验资料，同时引入修正系数0.75 来确定（不同土壤其系数有很大差别），亦或是16 h 后的试验数据，将其直接视为冻土的长期黏聚力。本文为了进一步降低试验误差以及数据记录的便捷性，设定球模仪压入时间为24 h，并采用24 h时所计算的黏聚力视为本次试验土样的长期强度。为消除土体表面因颗粒不均匀而导致测试结果的离散性问题，对每个冻融循环次数同时制取6 个平行样品，并取测试结果平均值作为参考。

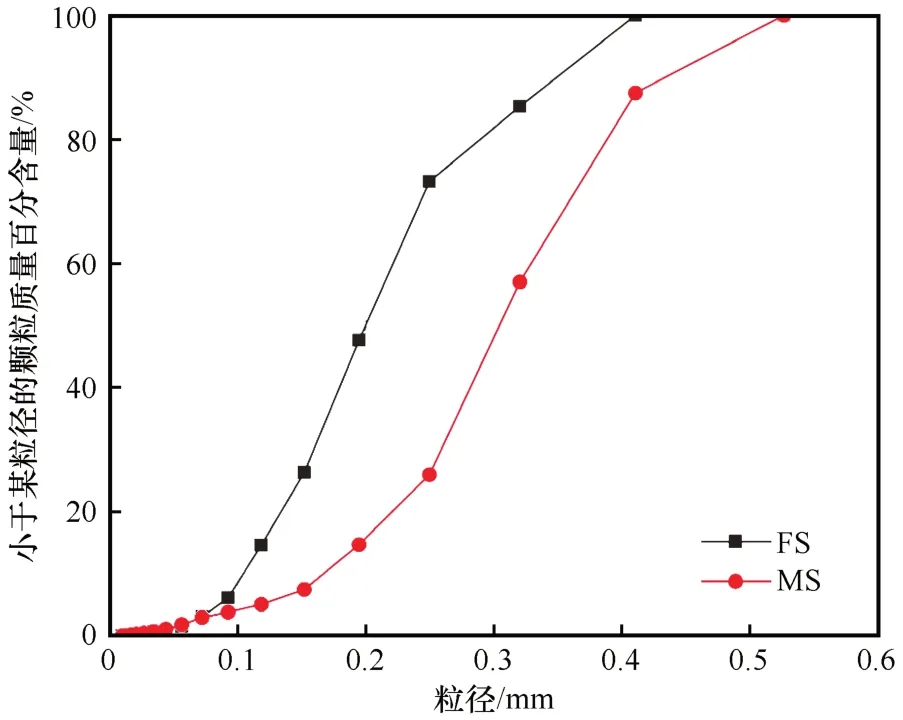
图2 颗粒级配曲线Fig.2 Particle size distribution curves of the soil

1.2 长期强度测定

球形模板压入仪（球模仪）是一种能够快速测出土体（冻结、未冻的黏土和冻砂等）黏聚力的试验装置（图3），测试原理与布氏硬度仪十分相似［23］。球模仪将土体视作理想黏结的不密实体，根据黏聚力与固定恒载下球形压在土体中沉陷深度的反比例关系进行推算。若固定恒载没有超出长期强度的极限值，则变形速度随着时间的累积而衰减，最终变形逐渐趋于稳定。

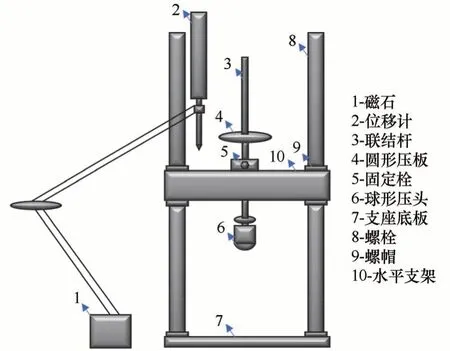
图3 球模仪结构示意图Fig.3 Structure sketch of spherical template indenter

冻土的抗剪强度由黏聚力和内摩擦力两部分组成，并在一定条件下满足库仑定律［23］。

式中：c(θ，ω，t)为冻土的黏聚力（MPa）；σ为法向应力（MPa）；φ(θ，ω，t)为冻土的内摩擦角（°）；θ为温度（℃）；ω为含水率（%）；t为时间（s）。

其中c和φ根据温度、含水率、作用时间来确定。将冻结的黏性土视为理想黏塑性体，此时tanφ(θ，ω，t)→0，式（1）可简化为

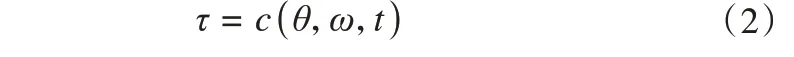
即冻土的抗剪强度实际上等于黏聚力，从塑性理论精确解答中推导其黏聚力的大小［18］。

式中：ct为随时间变化的黏聚力（MPa）；P为作用在球形压头上的固定恒载（kN）；K为修正系数，表示压板与土体的硬度比，塑性材料取0.18；d为球形压头的直径（mm）；St为球形压头在土中的沉入深度（mm）。

在固定恒载的作用下，球形压头沉入土中，用沉入深度St来计算冻土的黏聚力ct。黏聚力ct与压头接触面的最大接触压力存在一定联系，表述为ct=γq0，本研究中球形压头直径选用为22 mm［24］。由于受到内摩擦力的影响，将黏聚力ct视为等效黏聚力，其中包含了内摩擦力的影响。如图4 所示，随着时间的增加，球形压头沉入土中的深度受试验土样与球形压头接触面积的制约。球形压头与土体接触面积的增加，导致传入土中单位面积上的应力减少，从而加速了变形的稳定，所以利用球模仪测试土的长期强度非常节省时间，但由于得到的冻土黏聚力为等效黏聚力，是黏聚力和内摩擦系数的综合反映，而不是常见的摩尔-库仑准则中所用的单一黏聚力，因此所测的黏聚力通常要偏大［23］。

图4 球模仪球形压头压入土中示意图Fig.4 Sketch of ball indenter pushing into soil of spherical template indenter

使冻融试验箱的温度控制在-20 ℃，试验开始前（图3）首先检查螺栓、螺帽的松紧度，确保球模仪的正常使用。检查完成后，放置试样，使球形压头与试样上表面刚好接触，保持球模仪固定栓的松紧度。使用砝码施加竖向固定恒载，采用YHD-50型位移传感器测量球形压头的沉入深度，保持位移计的纵向竖直度，并将位移计归零。待温度稳定后，扭开球模仪的固定栓，开始进行等效黏聚力的测试，并利用计算机跟踪记录不同时刻下的沉降量。

1.3 土的分形特征

土是一种典型的多孔介质，从而导致传统的欧氏几何很难去描述［15］，分形理论的创立让描述土体不规则的特性有了新的发展，其主要通过分形维数来定量表征事物的复杂程度，其中分形维数包括Hausdorff维数DH、计盒维数DB等，由于计盒维数DB在数学上的便捷性以及物理上的直观性，成为了分形领域普遍采用的分形维数［25-26］。因此，本文利用PIP 9.1型颗粒图像处理仪所生成的颗粒显微图像，来分别测算经历不同冻融循环次数下土颗粒的计盒维数DB，从而进一步分析其变化规律。

如图5 所示的图像处理流程，首先利用PIP 9.1型颗粒图像处理仪将经历不同冻融循环次数下土的颗粒显微图像保存记录，使用ImageJ 图像处理软件进行图像类型转换、阈值调整、二值化处理等步骤。对于任意灰度图片其阈值范围为0～255，为选取一个合适的阈值将试样与其他部分分离，经过大量的测试后本文的阈值选取255。

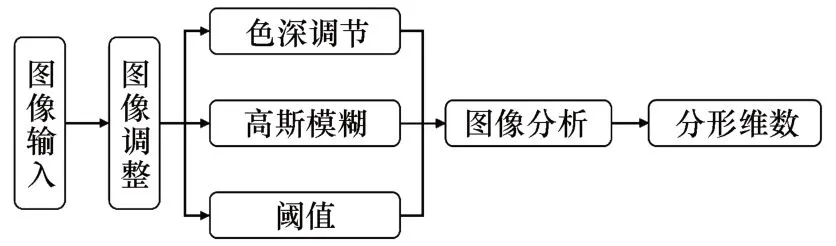
图5 图像处理流程Fig.5 Image processing flow

如图6所示，经过二值化处理后，可以清楚地看到颗粒的形态特征与分布情况，图中黑色区域即代表颗粒。用任意尺寸r＞0 的小方块（小盒子）将处理后的二值化图像进行网格划分，其中N（r）代表黑色像素所占有的网格个数。

图6 二值化图像示意图Fig.6 Schematic diagram of binarized images：raw image of PIP 9.1 particle analyzer（a）and image after binarization（b）

若存在数D，使得当r→0时

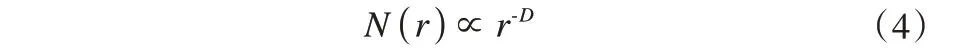
且仅存在唯一正值b，使得

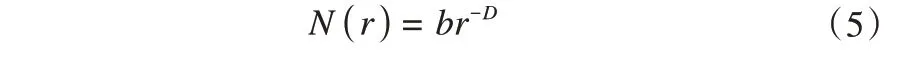
对上式两边取对数，可得

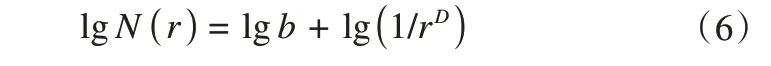
进一步化简为

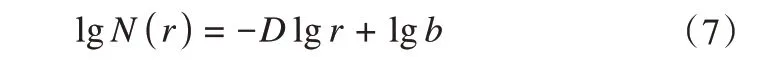
式中：D为分形维数，即所求的计盒维数DB。

在实际问题处理过程中，首先计算出覆盖土颗粒的网格数（盒子数）N（r），由式（7）可知，以lgr为横坐标，lgN（r）为纵坐标，在坐标系上使用最小二乘法对散点图进行拟合，利用拟合直线斜率来计算DB。需要指出的是，本文选取计盒方法所得的分形维数是仅具有统计意义上的分形维数，不同于颗粒形状与材质的严格意义上的分形维数。

2 结果与分析

2.1 长期强度的测试结果

使用球形模板压入仪进行冻土的长期强度测试非常节省时间，但由于土颗粒不均匀，球形模板压入仪的球形压头在压入时的测试结果出现很大的离散性［23］，因此进行多次重复试验是必不可少的。在经历4、6、10、50、100次冻融循环后砂土的长期强度变化特征如图7 所示，可以看到FS 与MS 的等效黏聚力均随着时间的增加而缓慢减小。

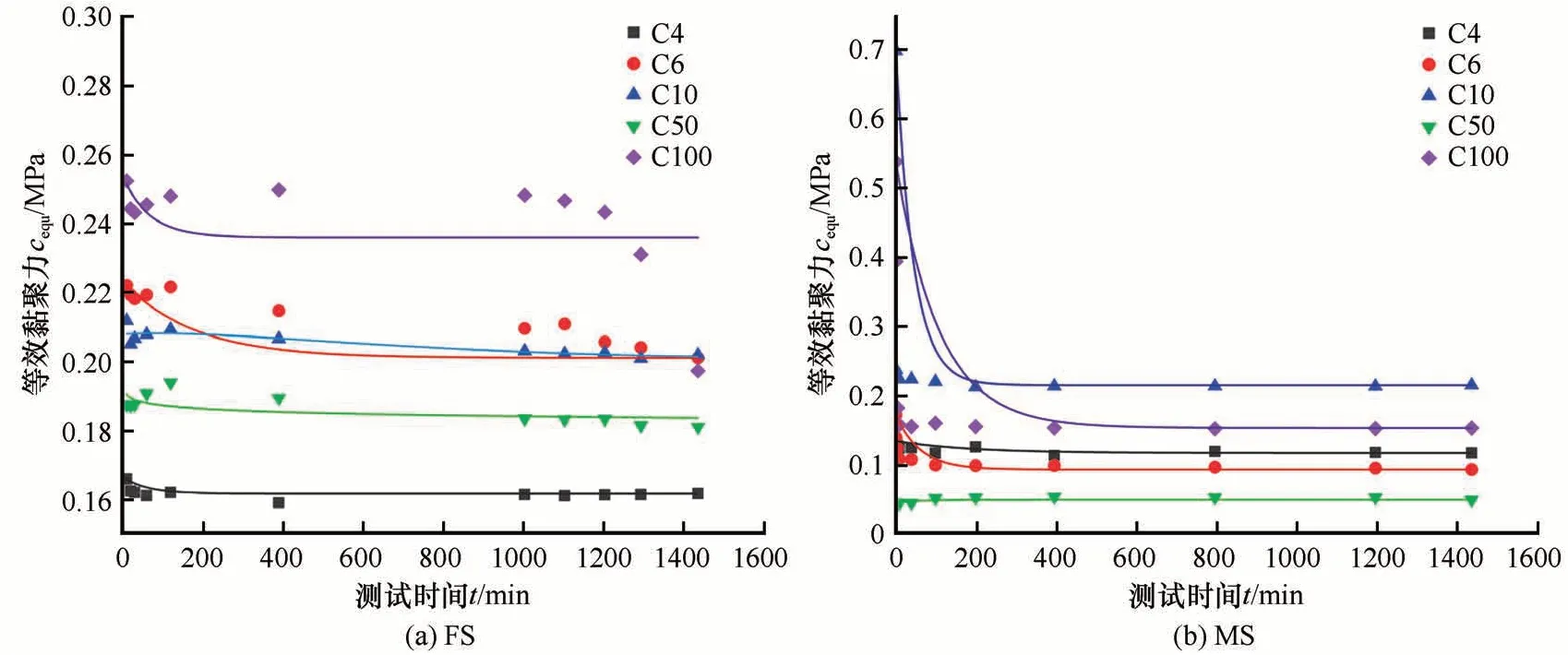
图7 冻结砂土的长期强度变化趋势Fig.7 Trend of long-term strength of frozen sandy soil

冻融循环作用使土颗粒之间产生较大的应力，颗粒反复发生分裂与团聚，并最终达到一种稳定状态［20］。值得注意的是，尽管土在宏观上表现出膨胀变形，但内部仍然进行着复杂的收缩膨胀现象，土样的干密度也发生变化，土颗粒的性质发生改变，这种宏观变化也是微观结构变化的一种表征［27］。可以看到在200 min 后，砂土的长期强度降低速度减缓，达到稳定状态，冻融前后的黏聚力降低接近50%左右，这与其他的学者［28］的研究结果相近。在此过程FS 与MS 表现出了冻结砂土的在蠕变过程中的塑性、黏性、弹性等性质。在竖向荷载的作用下，FS 与MS 在进行24 h 的测试后，认为此时试样的内部达到了稳定状态，测试的结果可以作为砂土的长期强度参考值［22］。如图8（a）所示，FS 在冻融循环10 次时的长期强度达到最大值，6、100 次时与10 次接近，稍低于10 次。50 次时的长期强度处于中间水平，4 次时的长期强度最低。在图8（b）中，MS 同样在冻融循环10 次时的长期强度达到最大值，在100 次时的长期强度低于10 次，处在第二级别。冻融循环4、6 次时的长期强度接近，均低于100 次，冻融循环50 次时的长期强度最低。长期强度是土体内部综合性质的表征，从两种变化曲线上来看，在经历10 次冻融循环后，砂土的长期强度均达到最大值，说明10 次循环后，试样内部的结构达到了一种稳定状态，抵抗外部荷载的作用有所增强。

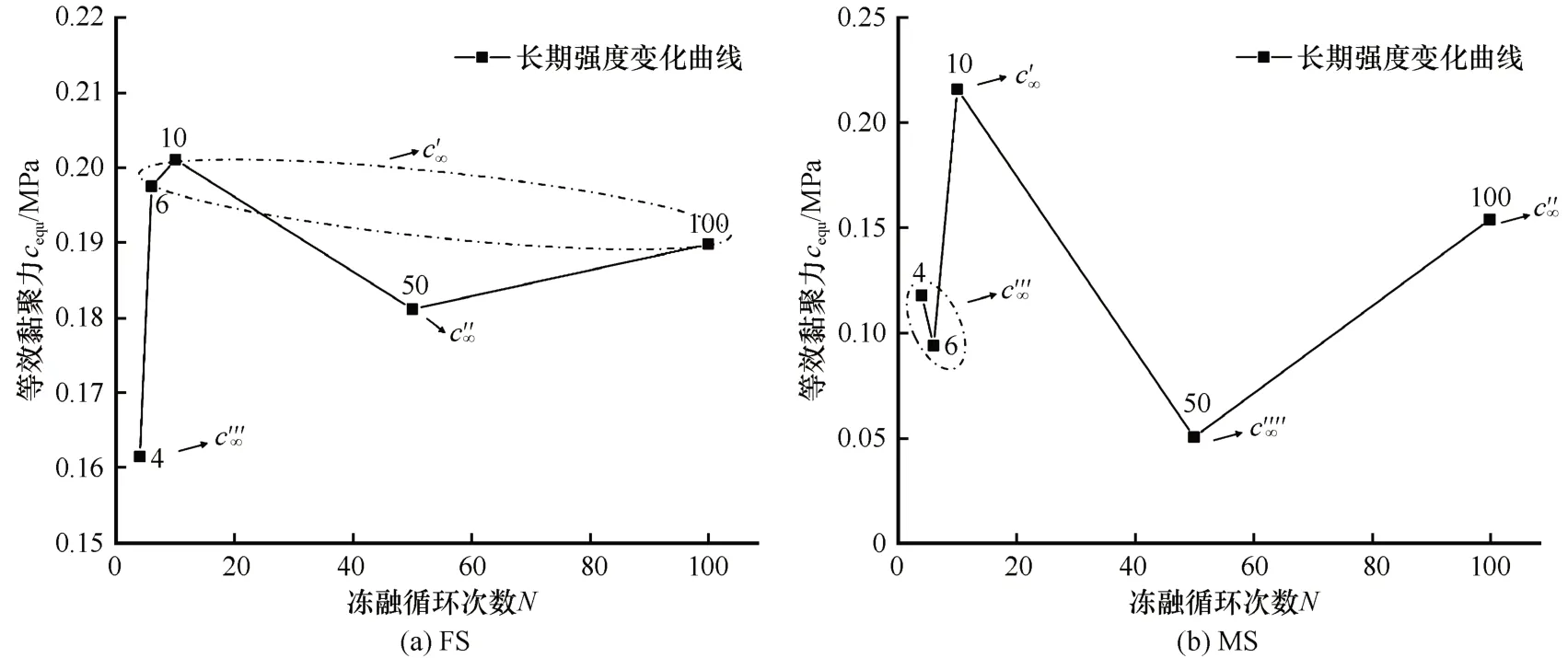
图8 长期强度随冻融循环次数的变化Fig.8 Variations of long-term strength with number of freeze-thaw cycles

2.2 不同冻融循环次数的分形特征

DB的计算结果如表1 所示，确定系数R2均在0.99 以上，说明试样具有良好的分形特性。FS 与MS的DB分别在1.3～1.7之间和1.4～1.8之间，平均值分别为1.478和1.594。

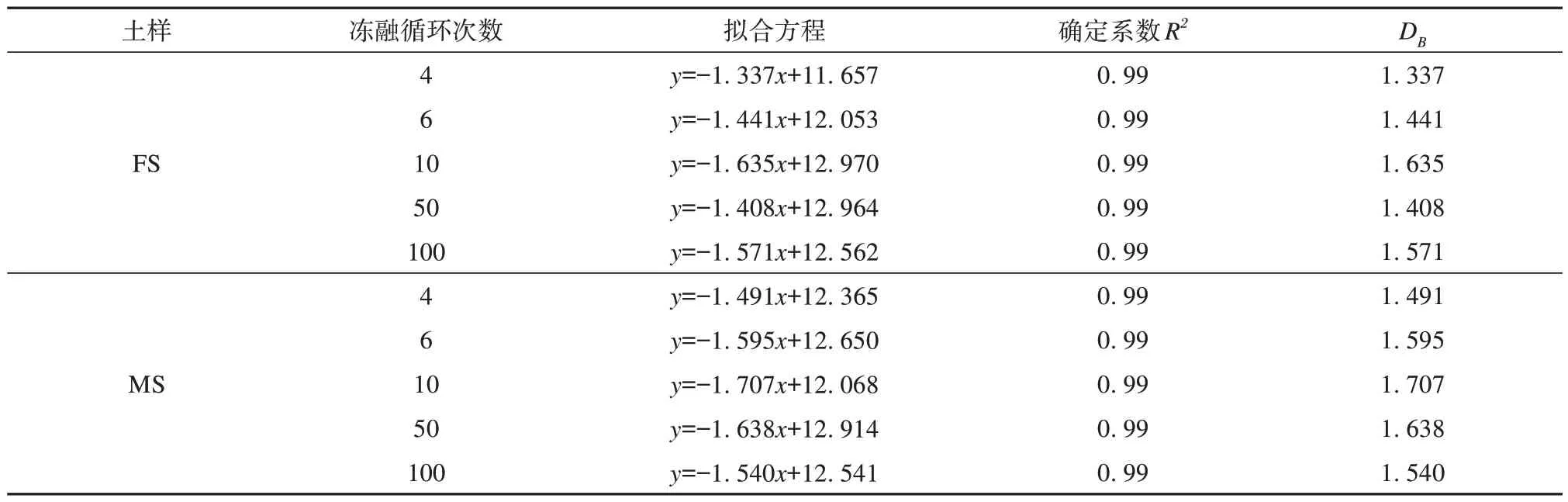
表1 不同冻融循环次数下砂土的分形维数Table 1 Fractal dimension of sandy soils under different number of freeze-thaw cycles

如图9 所示的DB随冻融次数的变化规律图，可以看到FS 与MS 的DB在10 次冻融循环以内随着冻融次数增加呈增大趋势（图9 中a 的位置），并在10次冻融后DB达到最大值。随着冻融次数的继续增加，MS的DB开始持续降低，并在10次至100次冻融循环中呈现线性趋势。FS 的DB在10 次至50 次冻融循环过程中与MS 趋势相同，但降低幅度（图9 中b的位置）远高于MS，在50次至100次冻融时，DB呈现增大趋势，100 次冻融循环后，数值高于MS（图9中c的位置）。随着颗粒破碎程度的增加，不同粒径的颗粒含量有所增加，试样所占有的像素比例增大，基于二值化图像所计算的DB也会增大。在反复的冻融后，颗粒有破碎集聚现象，不同粒级的混合程度降低，DB也呈现降低趋势。

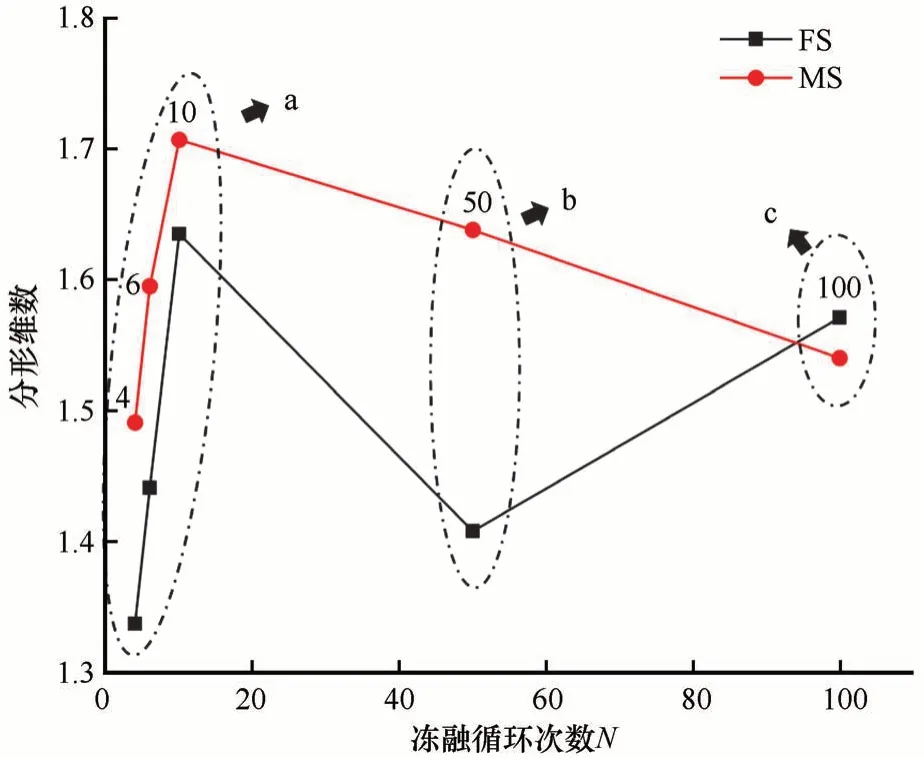
图9 分形维数随冻融循环次数的变化Fig.9 Variations of fractal dimension with number of freeze-thaw cycles

3 长期强度的影响因素

3.1 DB与长期强度的相关性分析

为进一步探究冻结砂土长期强度随DB的变化规律，将不同冻融循环次数下的长期强度与DB做相关性分析。如图10 所示，可以看到MS 的DB与长期强度确定系数R2为0.085，呈现微正相关。FS 的DB与长期强度确定系数R2为0.917，呈现极显著正相关。DB的大小可以集中地反映颗粒的分布分形特征，从图10（a）中可以看出，随着DB的增大，FS 的长期强度迅速增加，当DB达到最大值时，其长期强度同样达到最大值，可以利用FS 的长期强度与DB呈现高度相关的趋势来推测其长期强度的变化规律。图10（b）中所示MS 的长期强度变化在DB的增大过程中呈波动状态，第一阶段为强度上升阶段，强度增加0.036 MPa；第二阶段为强度下降阶段，降低0.104 MPa；第三阶段与第一阶段趋势相同，但幅度明显高于一阶段，强度增加0.166 MPa。MS的长期强度随着DB的增大并无明显的线性关系，总体上随着DB的增大呈现“竖向N”似的波动变化。

图10 分形维数与长期强度的关系Fig.10 Relationship between fractal dimension and long-term strength

3.2 粒组含量的变化

从DB的计算方法可以看出，长期强度与不同粒径的土颗粒含量密切相关。正如土质学家谢尔盖耶夫所言，粒度成分是决定土质最重要的因素，已有学者［21］对经历不同冻融循环次数以及不同细粒含量下的土颗粒的强度进行了分析研究，但并没有涉及土体在经历冻融循环作用后，内部的粒组与长期强度的变化规律。为进一步探究不同冻融循环次数下土体的粒组随长期强度的变化规律，将FS与MS 的颗粒尺寸分布分别以不同界限值划分为不同粒组，相关参数见表2～3。

表2 FS的粒径分组Table 2 Grain size grouping of FS

由图11（a）可知，随着冻融循环次数的增加FP1的粒组含量变化呈波动趋势，整体含量由冻融4 次的1.78%下降至冻融100 次的0.97%。FP2与FP3两个粒组含量变化呈现先增加后降低趋势，分别在冻融10 次以及6 次时达到峰值16.31%和19.68%。FP4的粒组含量总体上呈现阻尼形态波动，经历4 次冻融循环后达到最大含量46.98%，10 次后含量达到最低值13.20%，冻融100 次后含量与10 次相接近。

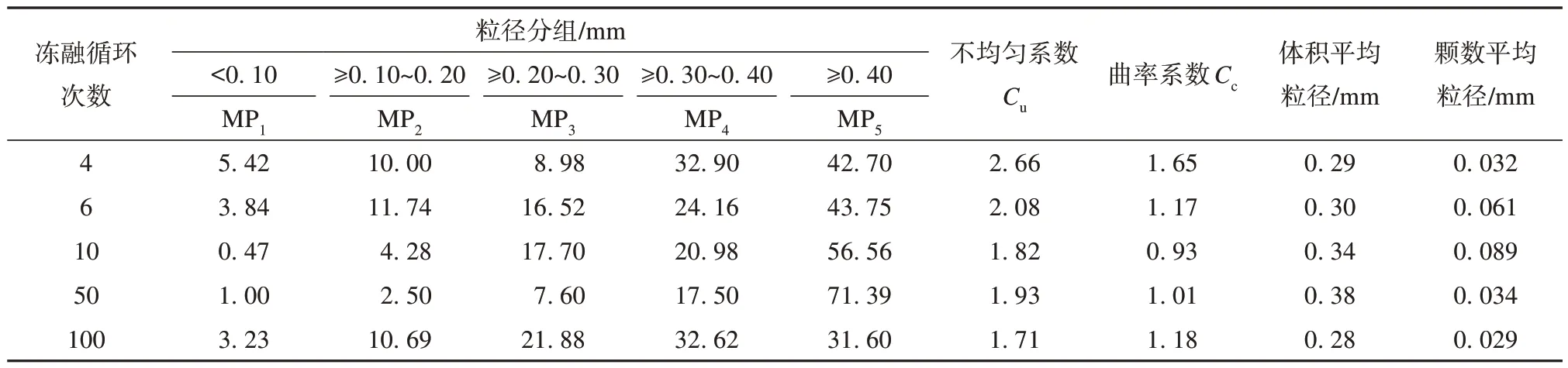
表3 MS的粒径分组Table 3 Grain size grouping of MS

这是由于在冻融作用的影响下试样内部发生了破碎集聚的现象。FP5的粒组含量在6 次冻融循环后达到最低值18.70%，继续冻融含量持续增加，在50 次后含量达到最大值34.23%。与之相反，FP6粒组含量在6 次冻融循环后达到峰值38.12%，8 次冻融循环后含量变化相对稳定，含量最大差值为7.97%，总体上与FP5的粒组变化呈共轭现象。FP7的粒组含量仅在土样进行100 次冻融循环后出现。如图11（b）所示，MP1、MP2和MP3的粒组含量在100次的冻融循环过程中，含量最大差值为4.95%、9.42%以及14.28%，粒组区间整体呈现扩大趋势。MP4的粒组含量在冻融循环过程中持续降低，在50次时达到最低值17.50%，之后继续冻融，含量有所回升。MP5的粒组含量与MP4的粒组含量变化也呈现共轭现象，在50 次冻融循环后含量达到最大值56.56%，随着冻融次数的增加，颗粒破碎，含量降至最低。

图11 粒组含量随冻融循环次数的变化Fig.11 Variations of coarse grain content with number of freeze-thaw cycles

3.3 粒度成分对长期强度的影响规律

为进一步分析不同粒组含量对冻结砂土长期强度的影响程度，将冻结砂土的长期强度与不同粒组含量绘制散点图，并利用最小二乘法进行拟合做相关性分析，结果如图12～13所示。FS中FP1、FP2与FP3的粒组与长期强度的确定系数R2分别为0.0208、0.1787 和0.1995，均呈现微正相关，结果表明［图12（a）～（c）］长期强度与这三种粒径级别的含量均没有明显的变化关联。当FP4粒组由13.20%变化至46.98%时，长期强度下降0.0402 MPa［图12（d）］，两者确定系数R2为0.9322，呈极显著负相关。FP5粒组变化与长期强度没有较强关联，总体呈下降趋势。随着粒径组别的增大，当FP6粒组由12.67%变化至38.12%时，长期强度呈现明显的升高趋势，长期强度提升0.0394 MPa，确定系数R2为0.5627［图12（e）］。由此可见，FP4与FP5粒径的百分含量对FS的长期强度起到关键性作用，可视为此类砂土的优势粒级。即当FP4与FP6粒组在一定区间内增加时，长期强度分别呈现减小和增大趋势，中间的FP5粒径级别视为过渡区域，含量变化与长期强度并无明显直接关联。

图12 FS不同粒组与长期强度的相关性Fig.12 Correlation between different grain group and long-term strength of FS

对于MS［图13（a）～（c）］，MP1、MP2和MP3的粒组和长期强度的确定系数R2分别为0.2744、0.4928和0.4343，呈现微负相关和负相关，长期强度随着这三种粒径级别的含量增加而缓慢降低。当MP4粒组由17.50% 变化至32.90% 时，长期强度由0.1178 MPa急剧降低至0.0504 MPa。而对于MP5，其变化呈相反趋势，长期强度增加0.1036 MPa。确定系数R2分别为0.8118 和0.8703［图13（d）～（e）］，呈现极显著负相关与极显著正相关。对于MS 而言，在冻融循环的作用下，长期强度的变化与MP4与MP5两种粒组密切相关，视为优势粒级。

图13 MS不同粒组与长期强度的相关性Fig.13 Correlation between different grain group and long-term strength of MS

4 影响机制分析

比较两种砂土的粒组与长期强度相关性曲线，可以明显发现，MS 的优势粒级范围（≥0.30～0.40 mm 与≥0.40 mm）明显高于FS 的优势粒级范围（≥0.15～0.20 mm与≥0.25～0.40 mm）。可见随着整体粒径范围的增大，长期强度会随着某些粒组在一定范围内的增加而呈现先降低后升高的趋势。这是由于当试验的颗粒构成发生改变时，试样的结构也会随之发生改变。在细颗粒达到界限含量前，试样以粗颗粒间接触以及和冰的接触为主要形式，极少部分的细颗粒以填充和被冰包裹的块状结构形式存在粗颗粒形成的骨架孔隙中，表现为以点接触的粒状堆积结构［29］。如图14所示，当细颗粒未充分地填充在粗颗粒的孔隙中，其孔隙率为21.298%；当细颗粒充分地填充在粗颗粒的孔隙中，其孔隙率仅为4.913%。

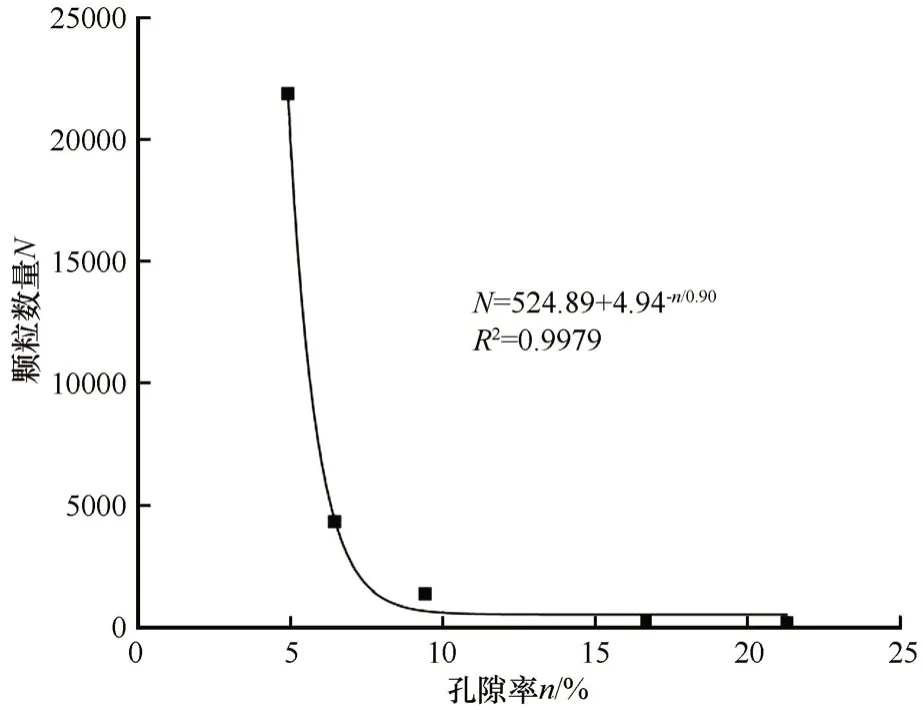
图14 孔隙率随细粒填充的变化趋势Fig.14 Variation trend of porosity with fine particle filling

针对细颗粒（FSC）的阈值含量，郭志杰［30］以最大干密度为评价指标，对粗-细粒混合土进行了一系列的室内试验，发现了随细粒含量变化的阈值为40%与85%。在本次试验中，FS 的FP4与FP6以及MS 的MP4与MP5均在含量接近40%时强度发生改变，这与其的研究结果相近。对于融土来说，根据细粒含量从低到高，可划分为接触状态1 至接触状态4 四个层次［31］。从完全由粗颗粒决定力学特性到完全由细颗粒决定力学特性，即从类粗粒土过渡至类细粒土，接触状态2、3 称之为中间性态土。与常规融土不同的是，在本次试验中试样均为饱和的冻结砂土，土颗粒之间由于冰的存在，在受到球形压头的作用后会发生流变现象。如图15 所示，在细颗粒达到界限含量（40%）以前，以粗颗粒间的接触以及和冰的接触为主要存在形式，并以粗颗粒和冰作为主要骨架，属于粗粒土的范畴，同时细颗粒会以填充形式存在粗颗粒与冰形成的孔隙之间，并充当“滚珠”的作用［32］。若细颗粒含量继续增加，由接触状态1 转变至接触状态4（图16），也就是由粗粒土范畴转变至细粒土范畴。而细粒土在空间中的填充度要优于粗粒土，此时试样以细粒土间的接触以及和冰的接触为主要形式，使得粗、细粒土间咬合比较紧密，粒间的胶结作用加强［30］，球形压头压入土体中所需要克服的阻力增加，长期强度表现出增大趋势。并且在一定范围内细颗粒含量的增加，会让细颗粒的“滚珠”作用进一步增强。同时随着整体粒径范围的增大，细颗粒的“相对粒径”也会增大，例如本次试验中FP4与MP4粒级，其含量在一定范围的降低导致土样长期强度的降低。随着粒径的增大，土样重新由粗颗粒和冰占据主导地位，长期强度又随着粗颗粒含量的增加而增大。冻融循环作用改变了粗、细粒土不同粒组的配比以及孔隙冰的变化，使得土颗粒接触状态发生改变，从而导致长期强度也随之发生变化。土体的力学性质受冻融次数与细粒含量的双重影响，对于不同条件下的试验，起主导作用的因素也不同，这也是土体性质受冻融循环作用呈现多样化的原因。

图15 细粒填充变化示意图Fig.15 Schematic diagram of variation of fine particle filling

图16 融土的接触状态示意图Fig.16 Schematic diagram of contact state of thawed soils

5 结论

在冻融循环的条件下，饱和冻结砂土内部的粒组成分会发生变化，同时影响着冻结砂土的长期强度，考虑冻融循环作用以及细粒含量对寒区工程建设非常重要，通过室内试验改变冻融循环次数来初步探究内部颗粒构成对冻结砂土的长期强度的影响，初步结论如下：

（1）FS 与MS 的长期强度均随着时间的增加呈现降低的趋势。在10次冻融循环后，冻结砂土的长期强度均达到最大值，FS 在4 次冻融循环后的长期强度最小，MS在50次冻融循环后的长期强度最小。长期强度是土体内部成分和结构的综合反映，两种砂土在10 次冻融循环后长期强度并无明显的剧烈波动特征，若在寒区进行相关的工程设施建设，建议在10次冻融循环后土体稳定时进行。

（2）基于分形理论，计算出FS 与MS 的DB在1.4～1.6 间波动，并在冻融10 次时均达到DB最大值。基于显著性分析理论，冻融过程中对于长期强度与DB的关系，FS 的拟合优度要大于MS。随着DB的增大，FS的长期强度呈线性增加变化，MS的长期强度呈“竖向N”似波动变化。

（3）冻融作用使FS 与MS 的颗粒粒组发生改变。FS 中PF4和FP6粒组与长期强度的拟合优度最好，确定系数R2分别为0.93 与0.56。MS 中MP4和MP5粒组与长期强度的拟合优度最好，确定系数R2分别为0.81 与0.87。FS 与MS 的长期强度变化的“优势粒级”并不相同，但“优势粒级”会随着整体粒径区间的增大而增大，这对于受冻融循环作用的地区预测长期强度具有重要意义。