基于NSGA-Ⅲ和道路运输能力饱和度的露天矿卡车调度优化方法

谭正华 宋港国 王李管 文 阳 李国泰

(1.湘潭大学计算机学院,湖南 湘潭 411105;2.湘潭大学网络空间安全学院,湖南 湘潭 411105;3.中南大学数字矿山研究中心,湖南 长沙 410083)

矿业历经了机械化、自动化时代,如今正步入智慧化时代[1-2],智能化和数字化是矿山发展的趋势,其中卡车调度的优化是露天矿山智能化建设的研究热点之一[3-5]。在露天矿的开采过程中,卡车的运输费用占了整个矿山生产成本的50%以上,卡车的非作业时间占了30%以上,合理高效地利用矿山设备不但可以减少对设备的损耗,也进一步降低矿山的生产成本,有效提升企业的市场竞争能力[6]。

国内外对露天矿卡车调度方法研究的文献较多,White J W 等[7-9]提出了两阶段法,该方法在LINGO上用数学方法求解线性规划模型,用动态规划求解实时调度模型。20 世纪70 年代末,美国Modular 公司开发的DISPATCH 调度系统就已经应用到实际的露天矿中。Souza 等[10]提出了混合式启发算法,赵勇等[11]提出了基于流率饱和度的露天矿卡车调度,邢军等[12]提出了基于产量完成饱和度的露天矿卡车调度。这些研究大多数基于矿山单个指标建立单目标车流规划模型对卡车进行调度,而企业通常需要解决涉及多个目标的问题,这些目标往往相互冲突,需要寻求最优的方案。

露天矿卡车调度已经由单目标问题转向多目标问题,多目标加权成单目标方法向多目标进化算法转化,多目标优化是一种考虑多种指标的寻优策略,更符合于实际问题的多种决策需求。在车流规划上,本研究以露天矿卡车总运输量和卡车非作业时间最小为目标函数,构建了露天矿卡车调度的车流规划模型,并基于多目标遗传算法在MATLAB 软件上求解。在实时调度上,本研究提出了一种基于道路运输能力饱和度的实时调度策略,并且和固定派车法组成综合派车方案。

1 露天矿卡车调度多目标优化模型

1.1 目标函数

露天矿卡车调度是一个复杂系统工程,实际问题经常涉及多个目标,这些目标往往是复杂冲突的。综合考虑矿山卡车调度的诸多因素,以卡车总运输量(t·km)最小,卡车非作业时间(h)最小为目标构建多目标优化调度模型[13-14]。

露天矿卡车调度模型概述如下:某露天矿实际开采中,有m个装载点Ai(i=1,2,…,m),有n个卸载点Bj(j=1,2,…,n),k辆卡车Cz(z=1,2,…,k),卸载点包括n1个破碎站和n2个渣场;装载点效率为T1(h/次),卸载点效率为T2(h/次);装载点Ai到卸载点Bj的距离为dij(km)(i=1,2,…,m,j=1,2,…,n);卡车的容量为c(t);卡车满载最大速度为V1(km/h),空载最大速度为V2(km/ h),卡车往返于装载点与卸载点之间;矿山工作1 个班时为T(h);第i个装载点矿石存储量为Q1i(t),第i个装载点岩石存储量为Q2i(t),第i个装载点矿石品位为Pi(%);第j个卸载点1 个班次产量的最低需求量为Q3j(t),第j个破碎站的品位要求上限为Q4j(%),第j个破碎站的品位值要求下限为Q5j(%);在装载点i和卸载点j之间的道路上运行1 趟的时间为T2ij(h);从i个装载点到j个卸载点最多能同时运行的卡车数为Aij(辆);1 个班次中,每辆卡车在这条路线上最多可以运行的次数为Bij;Xijz为第z辆卡车从第i个装载点到第j个卸载点次数。

模型的每一个目标函数由一个函数表示,所有的调度参数统称为X,构建的多目标优化目标函数如下:

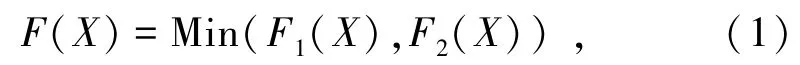
式中,F1(X)为总运输量;F2(X)为卡车非作业时间。

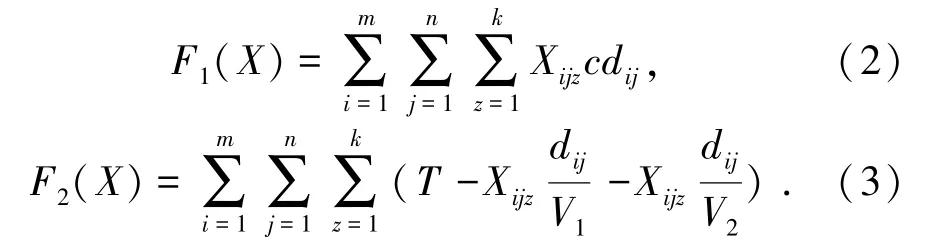
1.2 约束条件

(1)卡车从装载点运输出去的总量不能超过装载点的存储量。

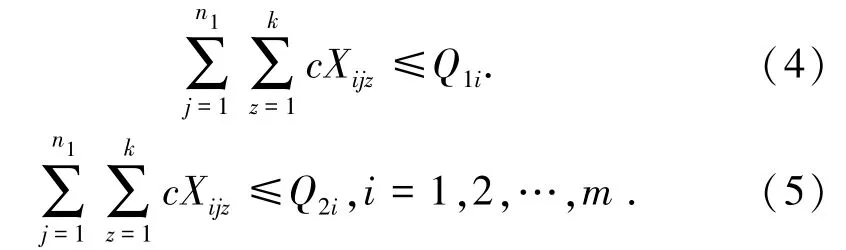
(2)产量不能低于卸载点的最低需求。

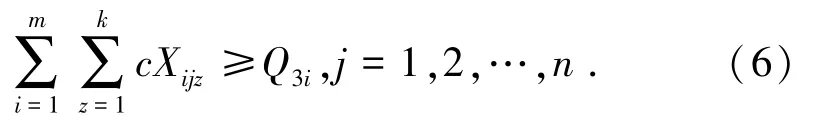
(3)1 个班次内,不能超过装载点的最大装车次数。

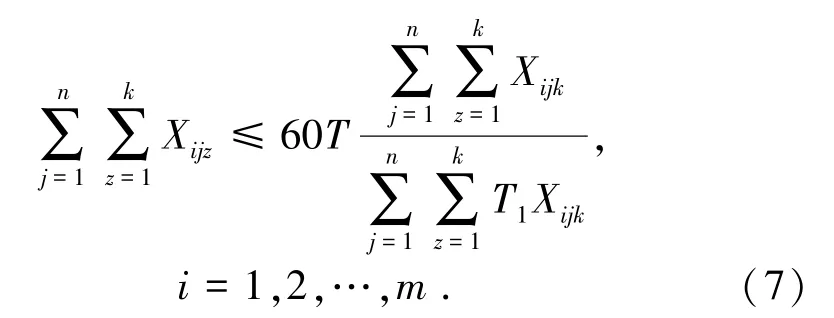
(4)1 个班次内,不能超过卸载点的最大卸车次数。

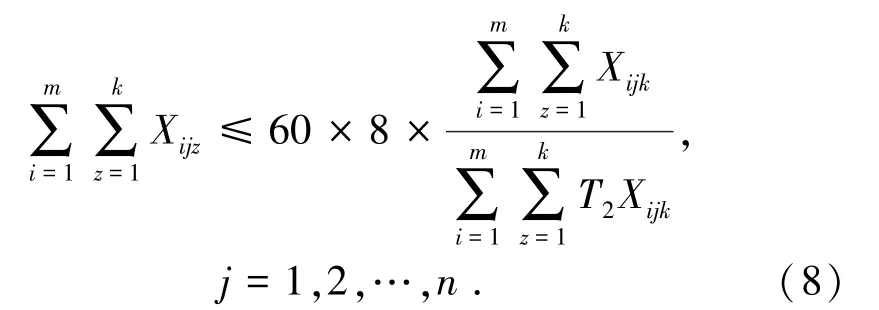
(5)满足破碎站(装载点包括破碎站和渣场)的品位限制。

(6)卡车运行1 个周期的时间包括重车行驶时间,空车行驶时间,卡车在装载点的装载时间,在卸载点的卸载时间。超过道路的饱和度,卡车在装载点或者卸载点会排队等候。

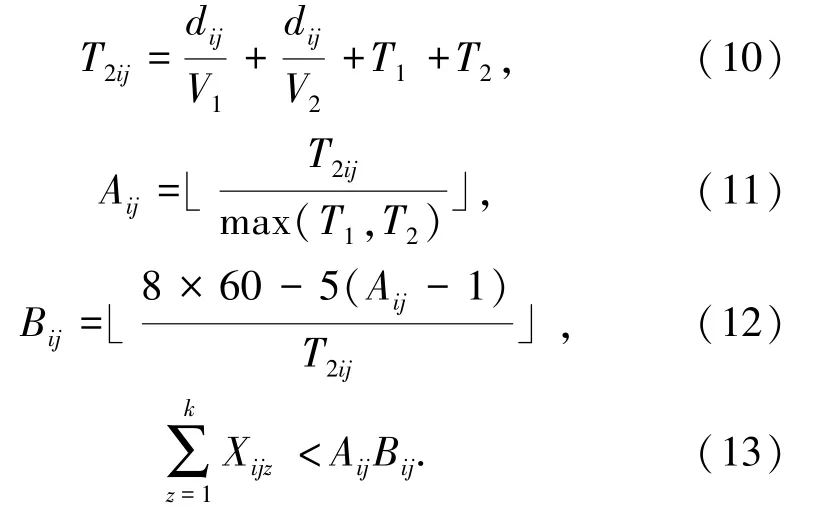
(7)不能超过卡车数量。

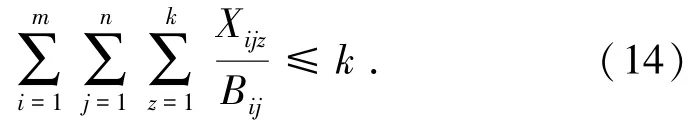
针对以上构建的多目标数学模型,本研究引入NSGA-Ⅲ算法进行求解。

2 露天矿卡车调度多目标遗传算法

2.1 多目标遗传算法

1975 年由美国J.Holland 首次提出的遗传算法(Genetic algorithm)[15]是一种随机搜索方法,其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,遗传算法可以自动获取并引导优化后的搜索空间,自适应调整搜索方向,无需特定规则。

由式(1)可以看出来:2 个目标是冲突的,一个目标变优,会导致另外一个目标变差,如果降低总运输量,就会使得卡车的非作业时间增大,从而降低了设备的使用率。多目标优化问题[16],目标往往是冲突的,需要找到平衡的折中解,因此引入Pareto 最优化理论。如果解x1在所有目标函数上的效果都比x2好,则称x1支配x2,如果在解集中,不存在任何一个解支配x2,则称x2为非支配解。所有的非支配解在笛卡尔坐标系下构成一个Pareto 前沿面。

对车流规划数学模型的解算,采用的是NSGA-Ⅱ算法[17],这是一种基于参考点的多目标进化算法。

2.2 算法核心思想

NSGA-Ⅲ是一种基于参考点的多目标进化算法,它与NSGA-ⅡⅠ[18]本质的区别在选择的机制上,本文不再赘述与NSGA-Ⅱ的相同的部分,只阐述优化问题求解过程中NSGA-Ⅲ的关键步骤。

2.2.1 归一化

遍历M个目标函数在每个目标维度i上的最小值,构成最小数值集合,按照下式标量化集合中的数值,可将目标函数fi(x) 转化为:

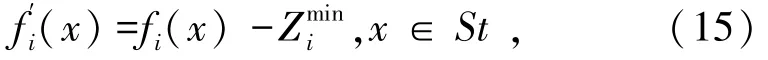
式中,St表示种群个体。

完成这一步后,接下来寻找极值点,为归一化做准备,需要用到一个名为ASF的函数,该函数定义如下:

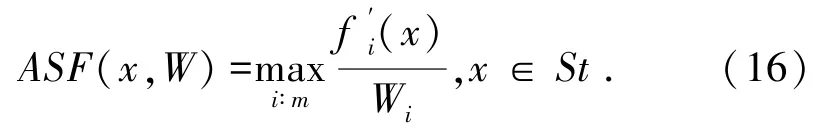
接着遍历每个目标函数,找到使得ASF数值最小的个体,这些个体就是Extreme Points,然后根据这些点的具体函数值,计算出对应坐标轴上的截距,截距的实际意义是每个坐标点在对应坐标轴上的坐标值,将其记录为ai。得到ai和Zi的具体数值以后,计算归一化的公式如下所示:

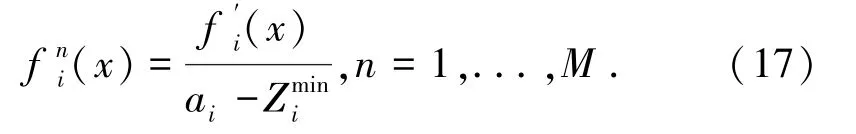
2.2.2 参考点的确定

归一化后,NSGA-Ⅲ的参考点可在归一化的超平面内进行:当有M个目标函数时,则可以围成M-1 个归一化超平面,假定沿着每一个目标函数所在轴进行p等分的话,则参考点可以选择H个。

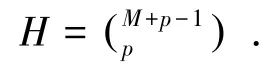
2.2.3 关键层解的选择策略

每个参考点可存在2 种情况,可能有一个或多个种群成员与它相关,或者不需要任何种群成员与它关联。

参考点设定之后,将已经在种群中的每个解都关联到一个参考点,关联之后,每个参考点j都会有1个与它关联的解的数量ρj。然后对ρj分情况讨论:① 如果这个参考点关联的种群个体数量ρj为零,但在第N层级的种群中有个体被关联到这个参考点向量,则从中寻找距离最小的点,并将其从N中抽取,加入到被选择的下一代种群中,设置ρj =ρj +1;② 如果在N中没有个体被引用到该参考点,则删除该参考点向量,如果ρj ＞0,则从中选择距离最近的参考点直到种群规模为N为止。

NSGA-Ⅲ流程图如图1所示。

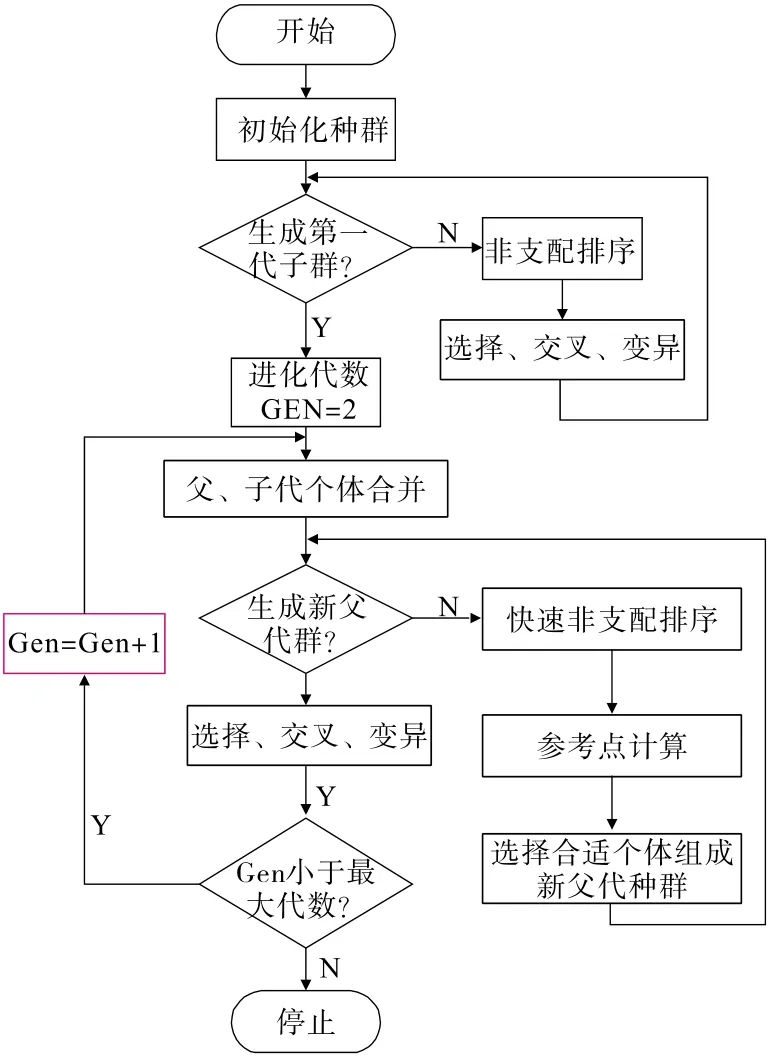
图1 NSGA-Ⅲ流程图Fig.1 NSGA-Ⅲ flow chart

2.3 测试函数

采用常被用作检测多目标进化算法搜索能力的多目标带约束的测试函数验证NSGA-Ⅲ算法的寻优性,以保证案例应用时候的准确性和可行性。

目标函数:

约束条件:

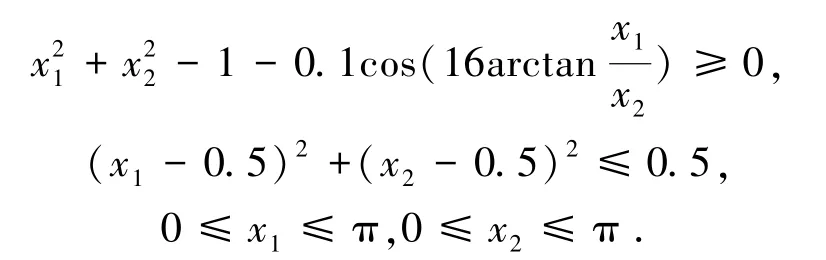
种群数量设置成100,采用实数编码,锦标赛选择,交叉算子设置为0.9,变异算子设置为0.01,迭代10 000 次,求解后优化结果如图2所示。Pareto 最优解集提供了多组解可供选择,并且分布均匀,具有良好的前沿面。

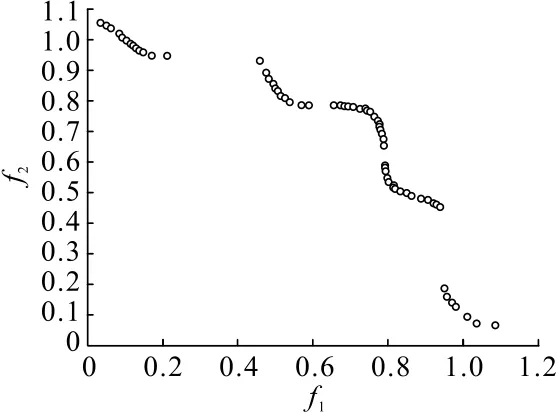
图2 测试函数优化结果Fig.2 Test function optimization results

3 道路运输能力饱和度和固定派车法的综合实时调度策略

本文提出的道路运输能力饱和度和固定派车法[19-20]的实时调度由3 个基本参数和3 个准则组成。

3.1 实时调度参数

在装载点i与卸载点j之间的道路R上,Tij是卡车运行一个周期的时间,包括重车和空车的行驶时间、装载时间、卸载时间;t1ij为卸载点j卸载时间;t2ij为装载点i装载时间;Aij为道路R中的卡车数量。

卸载点j的卡车饱和度系数:

表示因受限于卸载点的卸载能力,这条道路上最大的卡车数不能超过Kij,如果超过,卡车一定会在卸载点排队。

装载点i的卡车饱和度系数:

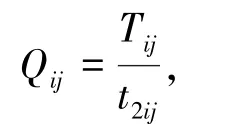
表示因受限于装载点的装载能力,这条道路上最大的卡车数不能超过Qij,如果超过,卡车一定会在装载点排队。

道路R的饱和度率系数

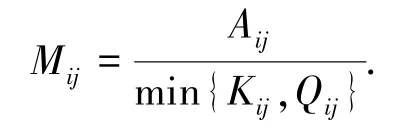
道路R上,min{Kij,Qij} 表示道路饱和度;当Mij大于1,卡车在装载点或卸载点一定会发生排队。

当卡车申请调度,根据车流规划,计算所有可以选择的道路的Kij,Qij,Mij。有了以上参数的计算结果之后,根据调度准则对当前卡车进行下一步安排。

3.2 实时调度准则

卡车T在i号卸载点和j号卸载点间的道路R上,将按照以下3 条实时调度准则对卡车进行安排。

准则1:将卡车T固定在道路R上运输,直到卡车申请调度。当卡车申请调度,转到准则2。

准则2:检查卡车T在R上的任务是否完成,如果完成,说明矿山系统正常,再检查卡车T在其他可以正常工作的道路上的运输任务是否完成,如果在别的道路上还有任务没有完成,基于道路饱和度将卡车T调往相应的道路R'去;如果卡车T在道路R上的任务没有完成,说明道路R上某个环节出现了问题,转到准则3。

准则3: 处理矿山系统因为任何事因导致i号卸载点和j号装载点无法正常工作的情况[21]。检查卡车T在其他可以正常工作的道路上的运输任务是否完成,如果完成,卡车T停止工作;如果没有完成,则基于道路饱和度将卡车调往相应的道路R'去,并固定在R'上,直到卡车T申请调度。矿山系统恢复正常后,卡车T需完成相应的任务。

以道路饱和度率系数Mij作为道路选择参数,准则2和准则3 将卡车派往到派往后道路饱和度率系数最小的Mmin对应的道路上。

调度完成后,更新各卡车的完成量。

实时调度流程如图3所示。

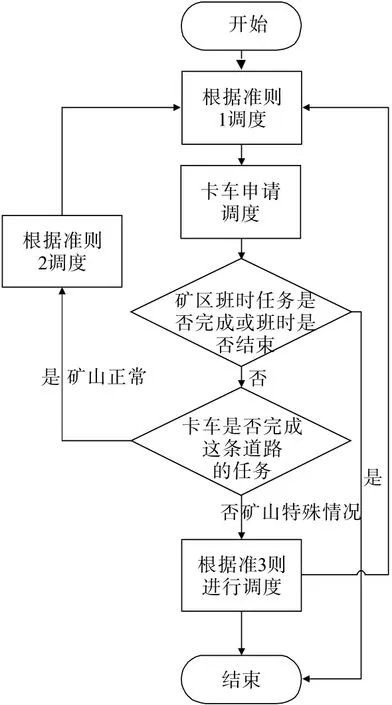
图3 实时调度流程图Fig.3 Flow chart of real-time scheduling

3.3 实时调度模型实现的目标

实时调度准则1和准则2,当矿山系统稳定时,实现车流规划的目标任务。卡车完成所处道路上的任务就申请调度,将卡车按照车流规划和实时调度准则派往对应的道路上,并固定在这条道路上运输,直到卡车申请调度。

实时调度准则3,对矿山系统不确定因素导致的特殊情况进行调度处理。当出现诸如装载点卸载点临时关闭,天气原因或者车祸等等导致道路临时封闭等一系列意外情况,卡车申请调度,对卡车进行安排。

实时调度准则在实现上述2 种目标的时候,有以下几个优点:卡车固定在某条道路,直到完成这条道路上的任务或者完成任务之前道路出现特殊情况,卡车才申请调度,这样可以避免卡车频繁的调动,节约矿山的成本和时间;不增加新的物理参数,只以道路饱和度率系数作为基础;整个实时调度模型的目标十分明确,尽最大可能保障卡车在装载点和卸载点不排队的同时,完成车流规划的目标任务。

3.4 与其他实时调度模型比较

建立装卸点路径列表和卡车任务列表,分别存储LP 需车路径和申请调度的卡车,优先级从列表自上而下依次递减。根据LP 生产路径下一次需要分配卡车到该路线上的预期时间,对LP 生产路径排序,预期时间最短者为最需分配卡车的LP 的生产路径,放在装卸点路径列表的第一行;根据卡车请求和即将申请调度的时间对卡车进行排序,申请调度时间最近者位于列表的第一行。然后依据预测的矿石损失吨位,将卡车任务列表中的所有卡车和装卸点路径列表进行匹配计算,将损失吨位最小者所对应的卡车派往最需车路线上去。DP 调度的优势在于兼顾已经申请调度和即将申请调度的卡车,从理论上而言,这是一种最佳配车方案,但在实际应用中也存在问题。动态规划调度算法是基于预测的,包括对需求时间和损失吨位的预测,在实际应用中预测的准确性很难把握,如果预测的时间过长,对预测的准确性很难把握,最大预测时间不能超过LP 最需车路径中的最短运行时间,如果预测的时间过短,则会造成每个时间段内可以统筹考虑的卡车数量过少,优化的实际意义不大;DP 调度不适合重车情形,需要单独处理重车调度;单个经济指标实现矿山卡车的分配。

Souza 等提出的混合式启发算法,结合贪心随机自适应搜索程序和一般变量领域搜索,优化了卡车调度中最少派车方案问题,这个方法虽然采用了进化算法增强了寻优能力,但这是一单个经济指标实现矿山卡车的分配。

基于流率饱和度的露天矿卡车调度和基于产量完成饱和度的露天矿卡车调度,同样是单个经济指标实现矿山卡车的分配,而且没法预测到下一次调度对卡车排队的影响,对于已经排队等候时间过长的卡车,系统需做出预警警报,并将卡车重新调度。

4 案例应用

某露天矿矿区有5 个装载点,4 个卸载点,运量为100 t 的卡车10 辆,由北斗导航监测系统测到各装载点和卸载点之间的距离如表1所示,装载点的存储量和品位信息如表2所示,装载点有3 个破碎站,1个班时的需求如表3所示。为了方便标识装载点、卸载点、道路、卡车,装载点和卸载点依次用罗马数字标识,卸载点i到装载点j的道路用i/j标识,卡车依次用阿拉伯数字标识。

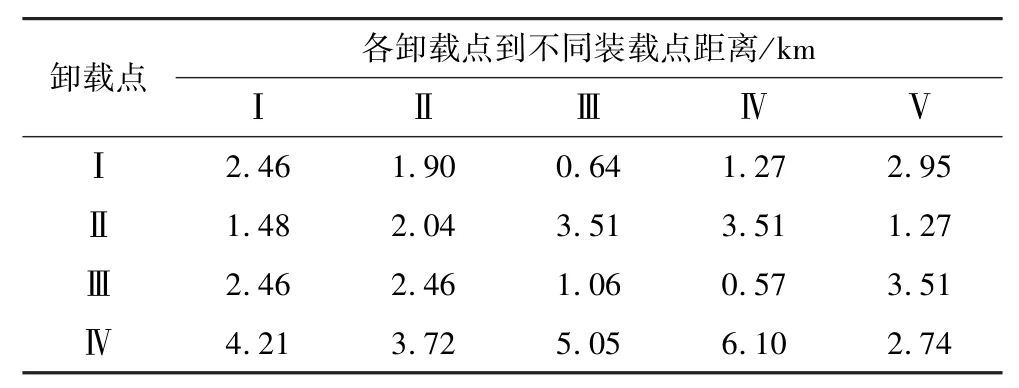
表1 装载点与卸载点之间的距离Table 1 Distance between loading point and unloading point

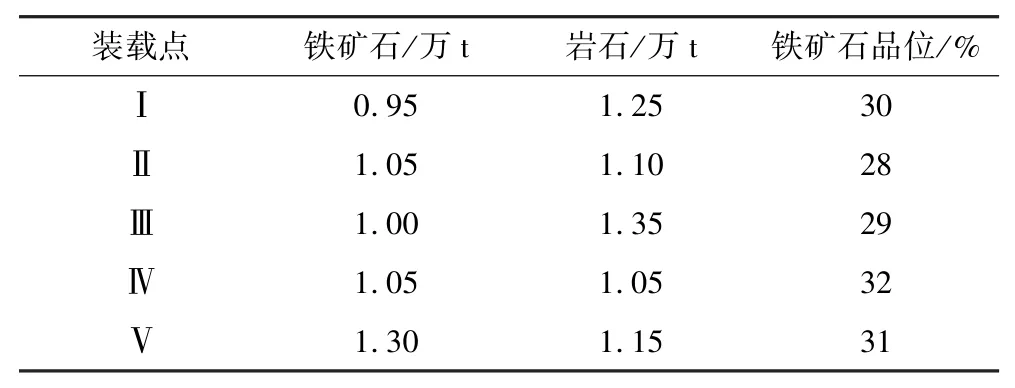
表2 装载点的存储量和品位信息Table 2 Storage capacity and taste information of the loading point

表3 卸载点1 个班时的任务需求Table 3 Task requirements for one shift at the unloading point

对于这样一个矿山,决策变量定义为单辆卡车在每条道路上的车次,所以决策变量的个数为200 个,约束条件个数50 个,在MATLAB 平台上编制NSGA-Ⅲ多目标遗传算法进行优化求解,其中种群数量设置为100,采用实数编码,锦标赛选择,交叉算子设置为0.9,变异算子设置为0.01,得到优化方案的Pareto最优解集如图4所示。

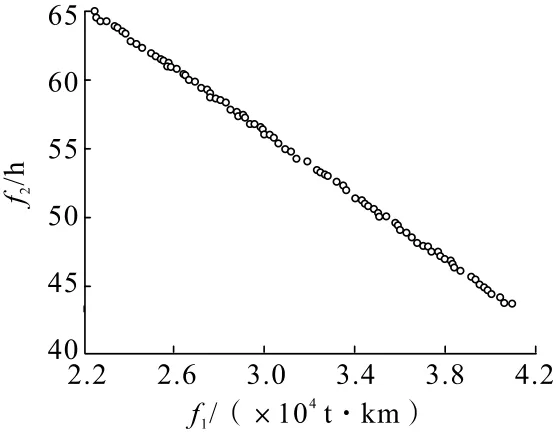
图4 10 辆卡车场景下的露天矿实例优化结果Fig.4 The optimization results of the open-pit mine example in the scene of 10 trucks

图4 中,f1表示总运输量,f2表示卡车非作业时间。从图4 可以看出,NSGA-Ⅲ求解得到了问题的若干个理想解,解集构成的Pareto 前沿面分布均匀,收敛性好,相比较单目标优化用数学的方法得到单个解,Pareto 最优解集能给调度人员提供更多的选择,调度工作人员可以根据矿山实际需求,合理地选择派车方案进行作业,达到总运输量最小并且充分利用卡车的目的。本研究通过依次减少卡车数量,得到完成矿山既定任务所需最少卡车数量,并得出每辆卡车的车流规划,如图5～图7所示。

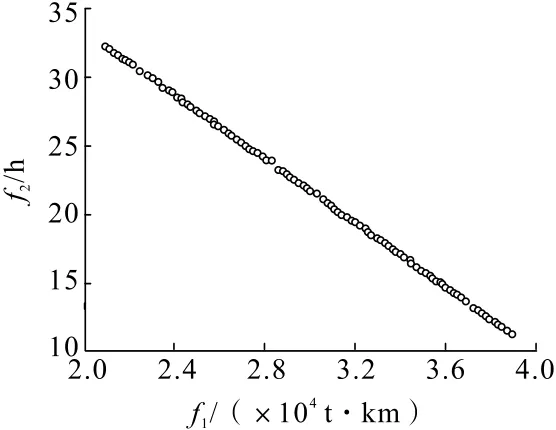
图5 6 辆卡车时的优化结果Fig.5 Optimization results when there are 6 trucks

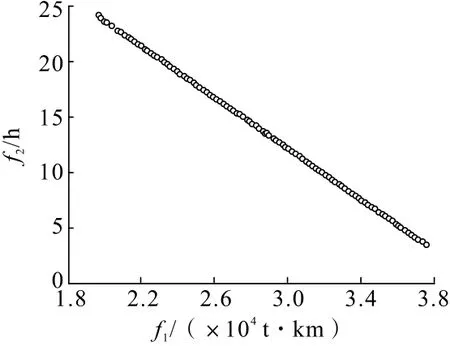
图6 5 辆卡车时的优化结果Fig.6 Optimization results when there are 5 trucks

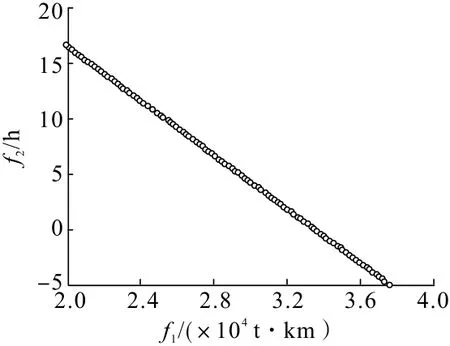
图7 4 辆卡车时的优化结果Fig.7 Optimization results when there are 4 trucks

根据图4～图6,卡车数量从6 辆到4 辆,总运输量基本不变的情况下,卡车非作业时间快速减少,但在4 辆卡车时,卡车非作业时间出现了负数,说明4辆卡车无法完成矿山的任务,因此得出在当前矿山情景下,最少5 辆卡车才能完成矿山的任务需求。以5辆卡车为例,各方案指标如表4所示。

表4 5 辆卡车各方案指标Table 4 Indicators of each program when there are 5 trucks

选择Pareto 上一组解,车流规划结果如表5所示。

表5 车流规划结果Table 5 Traffic flow planning results

每条道路饱和度如表6所示。

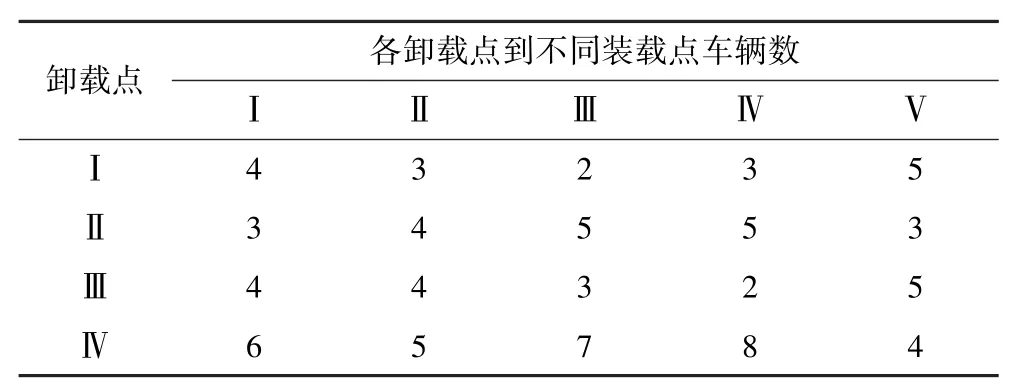
表6 道路饱和度Table 6 Road saturation

某个时刻,1 号卡车在Ⅰ/Ⅱ道路上运输,2 号卡车和5 号卡车在Ⅱ/Ⅰ道路上运输,3 号卡车和4 号卡车在Ⅲ/Ⅳ道路上运输,当1 号卡车申请调度,需对申请调度的1 号卡车下一步进行安排。根据车流规划给1 卡车分配的任务,据系统监测,1 号卡车还在Ⅰ/Ⅲ,Ⅱ/Ⅰ,Ⅱ/Ⅱ,Ⅲ/Ⅳ这4 条道路上有任务,并且这些路线都能正常作业,这4条道路的饱和度率如表7所示。

表7 道路当前的道路饱和度率Table 7 The current road saturation rate of the road

将卡车分别派往Ⅰ/Ⅲ,Ⅱ/Ⅰ,Ⅱ/Ⅱ,Ⅲ/Ⅳ这4条道路,4 条道路的饱和度率如表8所示。

表8 卡车派往后的道路饱和度率Table 8 Road saturation rate after trucks are dispatched

根据表8 可以发现,如果将1 号卡车调往Ⅲ/Ⅳ道路上,道路的饱和度率大于1,卡车一定会在Ⅲ/Ⅳ道路上的装载点或者卸载点排队,1 号卡车可以派往Ⅰ/Ⅲ道路和Ⅱ/Ⅰ道路,但不是最好的选择,派往Ⅱ/Ⅱ道路上,道路饱和度率仅为1/4,道路的拥挤度最小,所以理应将卡车派往Ⅱ/Ⅱ道路上。

5 结 论

基于多目标进化算法优化理论,综合考虑露天矿卡车调度各方面影响因素,以总运输量最少,卡车非作业时间最少,构建2 个互斥的双目标优化车流规划数学模型。由于卡车排队浪费过多的时间以及卡车在行驶和停止状态下切换耗油较多,该模型考虑每条道路上装载点和卸载点的饱和度,最大限度避免卡车在装载点和卸载点排队。经NSGA-Ⅲ算法解算,可以得出最少派车数量,以及给已经规划好的路线分配派车任务。

基于道路饱和度率的调度策略,与固定派车法组成综合实时调度模型,有如下几个特点:

(1)在矿山系统正常时,完成车流规划的同时,尽可能减缓道路拥挤程度,避免调度卡车而引起装载点或者卸载点排队,节省了矿山运输成本;避免了卡车司机随意申请调度,浪费太多时间在车流转移上。

(2)在遇到特殊情况时,该实数调度模型无需考虑何种特殊情况,只需考虑最终对装载点和卸载点的影响。

(3)不增加新的物理参数,只以道路饱和度率系数作为基础,与国外流行的动态规划模型相比,算法简洁合理,适应性强,适用面广。

该方法也存在需要改进的地方:实时调度阶段,为了减缓道路拥挤度,将卡车派往最不拥挤的道路上去,可能会造成装载点的铲车启动工作一会又陷入长时间等待,然后又启动,又等待周而复始的过程中,导致铲车效率不高。