基于扩展传染病模型的谣言溯源

吴 杨,吴国文,张 红,沈士根,曹奇英

(1.东华大学计算机科学与技术学院,上海 201620; 2.绍兴文理学院计算机科学与工程系,浙江 绍兴 312000)

0 引 言

随着社交网络的日益普及，微信、微博、Facebook等社交网络媒体飞速发展，如今成为人们生活必不可少的社交平台。这些社交网络平台为人们带来便利的同时，也带来了一些麻烦，网络谣言就是其中之一。在当今的社交网络上充斥着五花八门的谣言，有些谣言会导致个人的利益受损、影响金融证券市场稳定、社会混乱等问题。所以，分析谣言的传播过程并找出谣言传播的源头对于遏制谣言有十分重要的意义[1-6]。

近些年，谣言的传播溯源问题吸引了许多学者的关注。Comin等人[7]将接入性最大的节点推断为源头节点。Lokhov等人[8]通过找到传播边界概率最大的节点作为源头估计器的估计值。在另一方面，有的学者通过将拓扑结构与极大似然估计的方法结合来定位源头。这方面的开创者Shah等人[9-11]在susceptible-infected(SI)模型中，根据观测到的感染拓扑图，提出了一个谣言中心的概念，并且证明在树形网络下谣言中心就是最大似然估计的值。之后在此基础上，Luo等人[12]将谣言中心扩展到了多个源头的溯源问题中。文献[13-14]中基于极大似然估计提出局部谣言中心的概念，之后通过统计的方法求得信息源。Zhu等人[15]提出了基于最优样本路径的方法解决susceptible-infected-recovered(SIR)模型下的溯源问题，他们定义了一个感染偏心性，且具有最小感染偏心率的节点定义为拓扑图中的Jordan感染中心，然后证明了在树形网络中Jordan感染中心就是最优样本路径的源头，即源头的估计值。在文献[16]中Jordan感染中心被运用于多个信息源节点的源头检测问题。Kang等人[17]将溯源问题用于susceptible-infected-susceptible(SIS)模型中，Zhou等人[18]证明了Jordan感染中心的方法在susceptible-exposed-infected-recovered(SEIR)模型下溯源是可行的。此外，Pinto等人[19]在网络中设置传感器节点观测感染过程的方法，提出了感染时间差异的极限定理，并运用于溯源问题中。

社交网络中对传播谣言的节点具有检测能力，可对传播过谣言的节点进行隔离处理防止继续影响其他节点。根据谣言传播的性质，本文提出一种扩展传染病模型SIOR来分析单一谣言源头节点的传播与溯源。本文基于最优信息传播过程来求解谣言源头的估计值，并针对SIOR模型验证该估计值近似于网络拓扑中的Jordan感染中心。此外，本文还根据文献[15]中的RI算法，针对SIOR模型提出一种反向信息传递算法.并且在不同的网络模型下进行模拟实验，实验结果表明，该算法的溯源准确率要高于传统的中心性算法，同时还对比SIR模型的溯源效率，结果显示SIOR模型的溯源效率更优。表1列出了本文所用符号及含义。

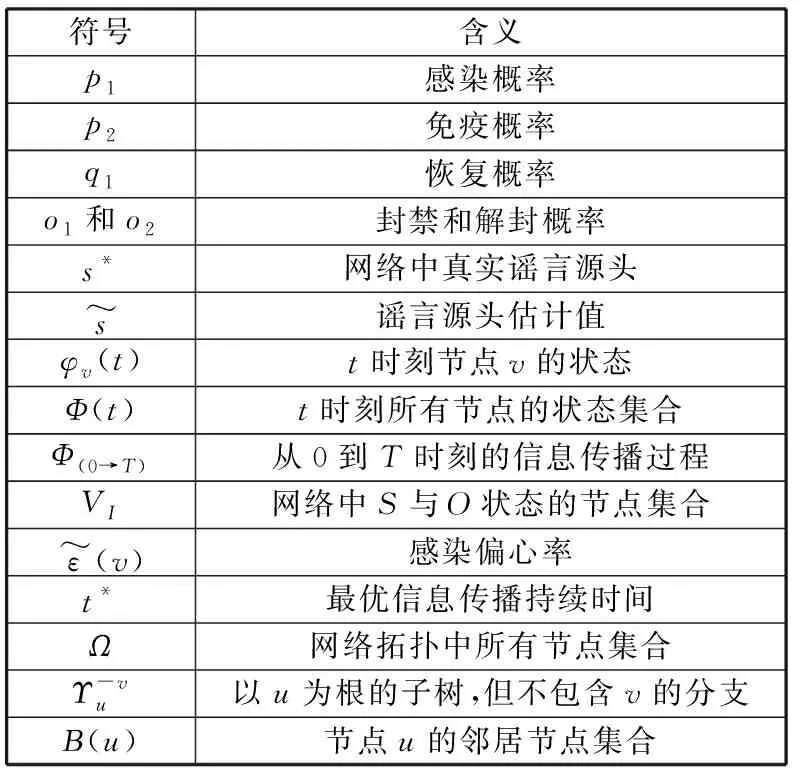
表1 本文所用符号

1 传播模型

1.1 SIOR模型

谣言在社交网络传播的过程中，节点的状态会发生一系列的变化，基于经典SIR模型提出的扩展型模型SIOR来研究单一信息源的溯源问题。

SIOR模型包含S、I、O、R这4种状态。图1给出了节点状态转换模型。S状态的节点在受到传播者传播的信息后，可能会以概率p1相信该消息，从而状态转变为I，同时也存在一些人，不会轻易相信该消息，或是可以辨别该消息是否属于谣言而以p2直接转换为R的状态，但必须邻居节点要为I状态时才会转换。而当一个节点属于I状态时，可能会以概率q1不再相信该信息转换为R状态，也可能被系统检测到传播谣言而进行封号处理，处于O状态不能继续发消息影响其他节点，在之后某时刻被解封转换为R状态。其中封号概率与解封概率分别为o1和o2。

图1 基于SIOR的状态转换模型

给定一个无向图G={V,E},V、E分别为图的节点集合和边的集合。每个节点v∈V包含S、I、O、R这4种状态。在信息的传播过程中，假设一个时间戳系统。当t=0时，图中节点只有一个感染状态节点即源头节点s*，其他的节点都处于S状态。每个节点只会在每个时间片开始的时候改变它的状态。例如：每个感染节点会在时间戳的开始把信息传递给它的邻居节点，而接收到的邻居节点会以p1的概率转化为I状态，而对于不相信该信息的人该节点会以概率p2转换为R状态。另外还假定变为R状态的节点不会再信任该信息，即不会再被感染为I状态。

由于节点状态的变化取决于邻居节点的状态或上一个时间戳该节点的状态，所以可以采用离散时间的马尔可夫链来描述某一时间戳节点的状态情况。令φv(t)表示节点v在t时刻的状态，令Φ(t)表示马尔可夫链，表达式为Φ(t)={φv(t)|v∈V}，作用是表示t时刻拓扑图中所有节点的状态。例如初始时刻t=0,表示为：

φs*(0)=I，Φ(0)={I,S,S,S,S,…,S}

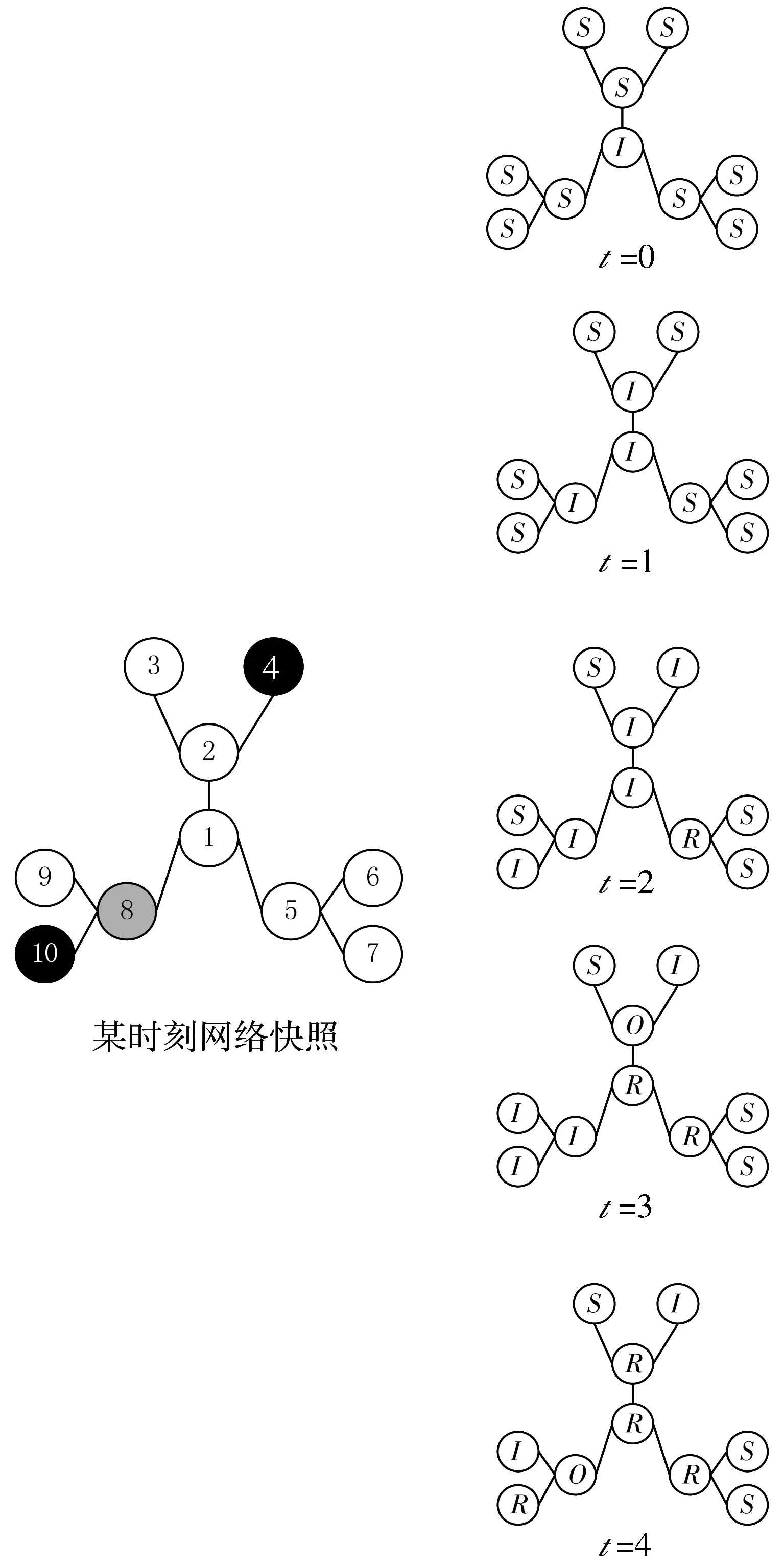
图2 节点状态转化过程

在图2中，时间戳t=4时节点的状态为：

Φ(T)={S,I,R,R,R,S,S,O,R,I}

1.2 观测网络模型

要获取传播过程中某一时刻的拓扑图，定义Ω={ωv,v∈V}来表示观测快照中节点的状态，根据真实的情况，观测快照是无法区分S状态和R状态的节点，则可以通过一个函数来表示节点的状态：

(1)

例如在t=0时观测快照的节点状态集合为：Ω={1,0,0,…,0}，在图2中左方的图为观测快照图，该快照的节点状态集合表示为：

Ω={0,0,0,1,0,0,0,2,0,1}

1.3 信息传播过程

定义1 从0时刻到T时刻，信息传播的过程为：

Φ(0→T)={Φ(t):0≤t≤T}

(2)

其含义为每一个时间戳的节点状态集合的集合，同时为了将信息传播过程中的节点状态与观测到的快照的状态信息对应起来，定义一个映射函数：

(3)

如果在某一时刻观测到的快照的状态与某一个传播过程的状态完全相同，即Γ(Φ(t))=Ω成立，则称这是一个可能的传播过程，这个传播过程从0时刻到t时刻最终的状态与快照状态一致。举个例子，在图2的传播过程中，左方的图是某时刻观测到的网络拓扑Ω，黑色的节点表示处于I状态,灰色节点表示处于O状态，白色节点表示处于S状态或是R状态的节点。右方的图表示某一信息从0时刻到t时刻的传播过程，当t=4时网络拓扑与观测到的快照的拓扑的状态信息完全吻合，于是称该过程是一个可能的传播过程。

2 谣言源头估计器

2.1 极大似然估计器

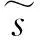
(4)

其中，Ρr(Φ(0→T)|s*=v)表示当起始节点v为给定的源头时，形成传播过程Φ(0→T)的概率，而Φ(0→T):Γ(Φ(t)=Ω)表示以节点v为起点所有可能的信息传播过程，即这些过程在t时刻的节点状态与观察到的快照Ω的状态相同。

但是，假设传播过程执行了t个时间戳，在观测快照拓扑Ω获取了I和O状态的节点一共有N个，则可能的信息传播过程至少有tN个，要解决这个指数级别计算问题十分困难，所以下面给出最优信息传播过程的概念，来化简这个问题。

2.2 基于最优信息传播过程的估计器

为了能够简化信息源溯源问题，参考文献[15]，可以通过构建最优信息传播过程，来降低极大似然溯源估计器的复杂度。

定义2 一个最可能在[0，T]时间内形成观测快照的拓扑Ω的信息传播过程称为最优信息传播过程。表达式为：

(5)

其中,t*是最优信息传播过程的传播时间。规定能形成最优传播过程的起始节点作为信息源的估计值，即基于最优传播过程的源头估计器。简单地说，最优信息传播过就是一个最有可能导致最终观测快照的感染过程。

3 基于最优信息传播过程的溯源方法

3.1 Jordan感染中心

在对该检测方法进行分析前，参考文献[15]给出拓扑图中节点性质的定义。

定义3 在观测快照的拓扑Ω中，使用d(v,u)表示任意2节点v和u的最短距离，任意节点v到距离它最远的I状态或是O状态节点的距离为该节点感染偏心率，表达式如下：

(6)

其中v∈V，VΙ表示快照Ω中I状态和O状态节点的集合。再根据乔丹中心的定义，给出乔丹感染中心的概念，即快照拓扑Ω中具有最小感染偏心率的节点，表达式为：

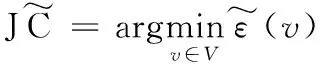
(7)

3.2 最优信息传播持续时间

本节将通过定理1表述在谣言传播的网络中，一个最优信息传播过程的持续时间近似于该过程起始节点的感染偏心率，以及信息传播过程持续的时间越长，信息传播过程发生的概率就会越低。且本文将针对无限的正则树网络构建溯源模型，因为在通常图结构中获取最优信息传播路径还是困难的，并且在正则树网络中节点的度值相同且没有回路。

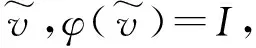
(8)

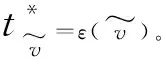
(1-p1-p2)|Β′(u)|p1·q1·p2(1-p1-p2)|Β′(u)|}

(9)

下一步假设最大距离为k=n时成立，验证k=n+1。先将树形网络划分为多个子树结构，对于每个子树上应用归纳假设的方法，给定一个持续时间为t+1的最优信息传播过程，总是能构建出一个同源且持续时间为t的信息传播过程，其发生概率更大。如式(10)所示。

(10)

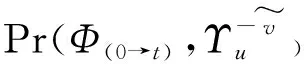
3.3 感染偏心率

本节将证明在网络拓扑中，最优信息传播过程的起始节点的感染偏心率越小则该信息传播过程的发生概率就越大。

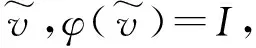
(11)

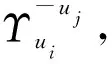
(12)

根据该过程，总是能构建出一个发生概率更高的信息传播过程且它的起始节点uj的感染偏心率更小。其发生概率的表达式为：

(13)

根据上述不等式易知式(13)>式(12)，即不等式(10)获证，定理2证毕。

3.4 谣言源头估计值

本节将说明Jordan感染中心是最优信息传播过程的源头，且可以作为谣言源头的估计值。

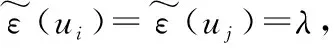
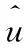
根据以上3个定理可知，最优信息传播过程的源头可以作为谣言源头的估计值，且该值近似于网络拓扑图中的Jordan感染中心。

4 实验仿真及分析

4.1 反向信息传播算法

根据上文证明可知，评估源头需要先找到拓扑图中所有节点的感染偏心率，再进一步找到Jordan感染中心，根据文献[15]中RI算法，本文提出针对于SIOR模型的反向信息传播算法。

算法1 反向信息传播算法

输入：节点集合VI和网络拓扑Ω

步骤1 初始化2个集合，一个为记录发送信息的节点sent_list，一个为记录接收信息的节点receive_list，并且为所有节点加入一个记录节点ID的数组，一个计数器及一个总时间属性。并让系统的时间t=1，将所有VI中的节点加入到sent_list中。

步骤2 遍历sent_list中的节点，判断它们的邻居节点是否为第一次收到ID信息，如果是则记录该ID到节点的数组中，同时更新计数器以及时间和属性，并把节点更新到receive_list中。如果计数器的值等于VI中节点数量，表明该节点可以作为可能的估计值并加入到结果集中，更新循环结束标志。当遍历完一轮后，系统时间t=t+1。最后将receive_list中的节点更新到sent_list中。如果循环没结束，重复步骤2，否则进入步骤3。

步骤3返回结果集，如果存在多个节点，返回总时间最小的节点，该节点就是拓扑结构中的Jordan感染中心。

4.2 实验评估标准与数据集

为了验证求解Jordan感染中心的(Jordan Centrality， JC)反向信息传递算法的有效性，本文将与其他中心性算法进行比较，包括度中心性[20](Degree Centrality， DC)，接近中心性[21](Closeness Centrality， CC)，中介中心性[21](Between Centrality， BC)。并且采取表2所述的网络数据集，比较算法的检测效率。同时为了更好地描述实验的结果，本文采用文献[22]中溯源的衡量标准。

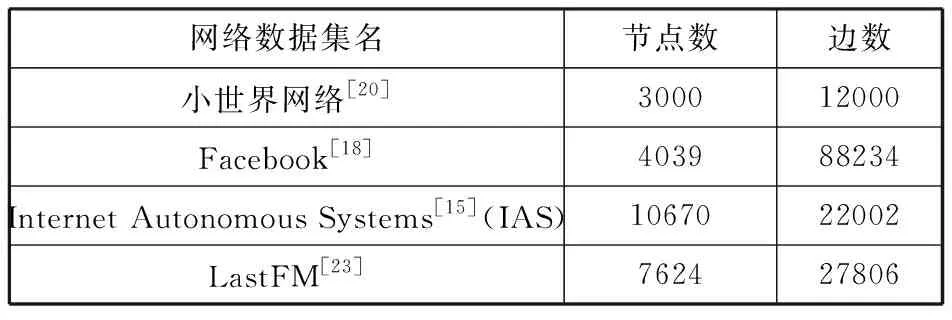
表2 网络数据集

1)检测准确率(Detection Rate)。

检测准确率表示多次执行算法后，正确找出源头的次数与总次数的比值。

2)检测误差(Detection Error)。

检测误差表示算法得出的估计值与真实源头之间最短距离的平均值。

4.3 实验结果及数据分析

本文首先在不同度值的正则树形网络中比较3种算法的检测准确性。分别构造度值为2～6的正则树，在网络中随机选取一个节点作为谣言源头，对于每种度值进行模拟传播过程1000次，其中对于感染概率p1随机从(0,1)中选取，对于恢复概率q1与封号概率o1从(0,p1)中选取，而对于概率p2与o2尽可能取值偏小，选取观测快照的时间在区间[3,10]中，这主要是为了保证有足够多的节点被观测到，且让正则树尽可能保持无限大。结果如图3所示。可以看出，对于每种度值的正则树形网络JC算法的溯源准确度高于其他中心性算法，由于正则树中节点的度值相同，所以DC算法准确率偏低。且当度值为6时，JC算法溯源准确率达到了61%。

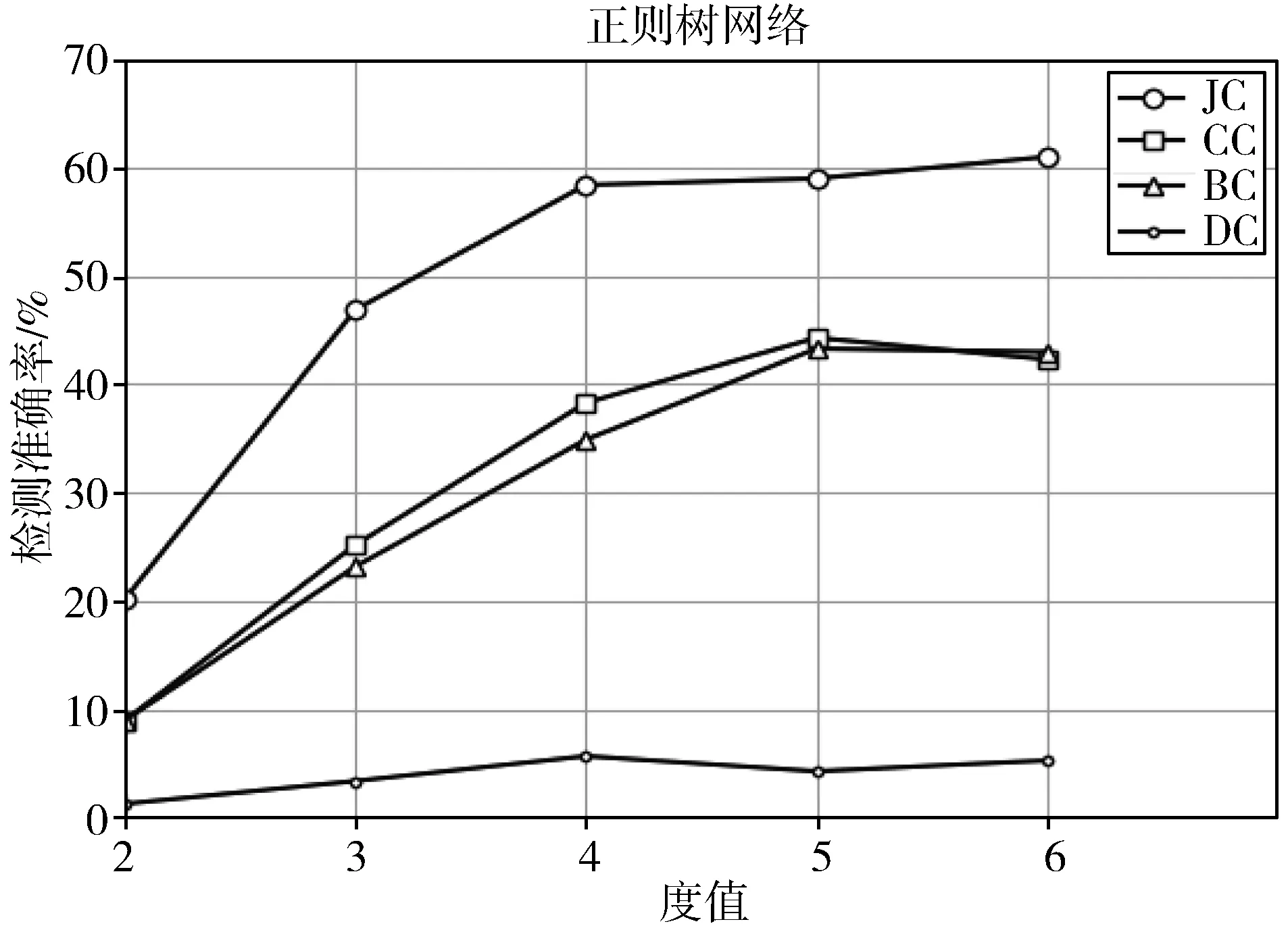
图3 正则树网络中实验结果

接下来，本文在复杂网络中进行对比实验，选取小世界网络[20]，构建3000个节点和12000条边。为了保证传播能在一个足够大的网络中进行，将选取尽可能小的概率，其中对于感染概率p1随机从(0,0.05)中选取，对于恢复概率q1与封号概率o1从(0,p1)中取，而对于概率p2与o2尽可能取值偏小，获取观测快照的时间选定在观测图中感染节点超过100个时，进行1000次模拟。实验结果如图4所示，不难看出，JC算法的溯源距离主要分布在0～1跳内，而传统中心性主要分布在1～5跳内，0跳时，JC的准确率为46.2%。

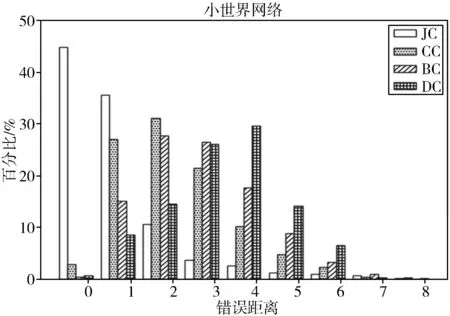
图4 小世界网络中实验结果

本文下一步在真实网络中进行模拟实验，在Facebook网络、Internet Autonomous Systems网络以及LastFM Asia Social网络中进行传播模拟，同样为了保证传播过程能在一个足够大的网络中进行，概率与快照观测时间选取与前一部分小世界网络中实验配置相同，进行1000次模拟，实验结果如图5所示。很容易看出JC算法在不同网络中检测出的平均误差距离均要小于CC和BC检测算法。由于真实网络中存在较多的边，网络中存在度值较大的节点，因此谣言扩散更快，溯源准确率偏低。对比于小世界网络，其节点度值平均，JC算法检测更加准确。

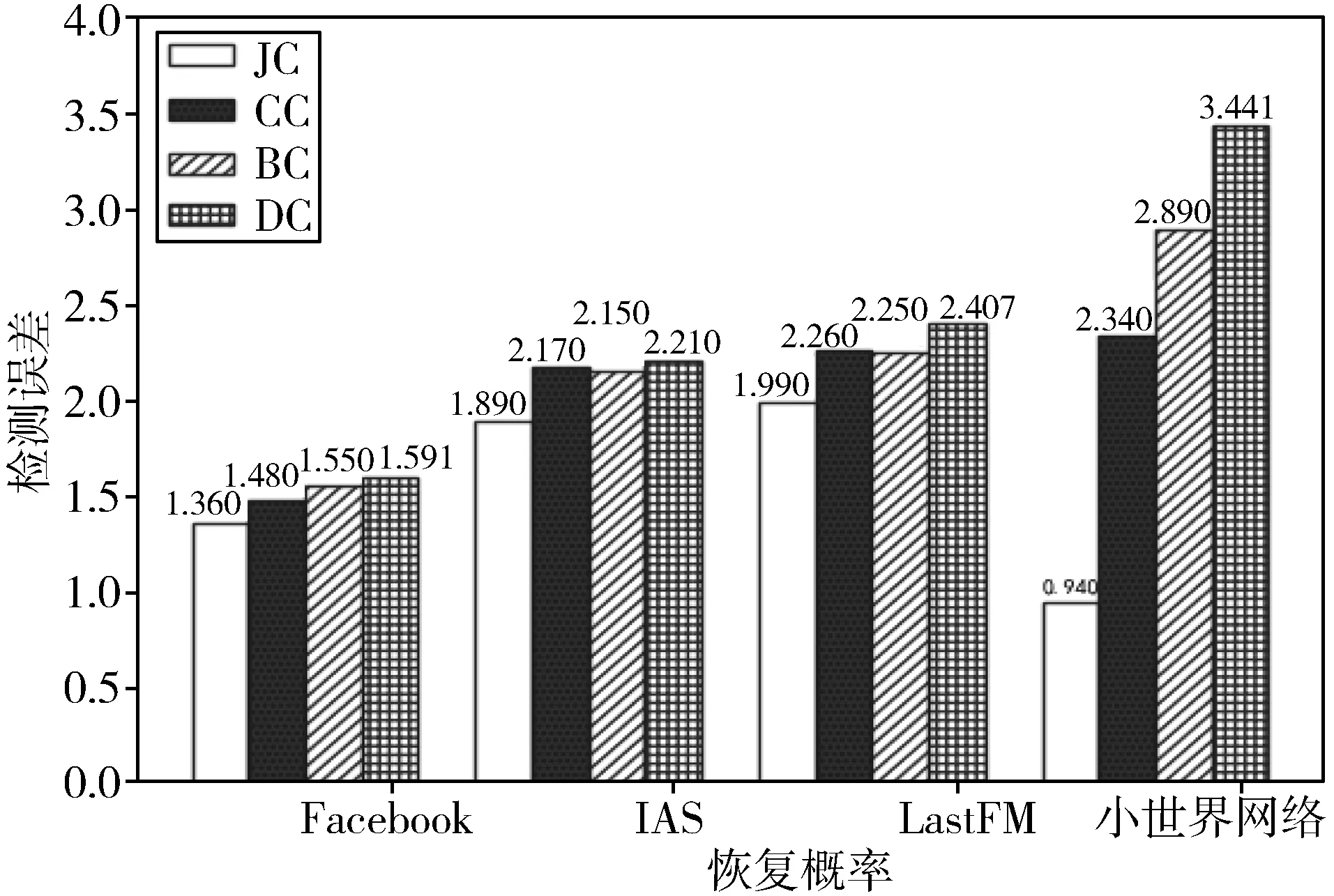
图5 真实世界网络中实验结果

最后，本文在度为3的正则树网络中进行SIR模型与SIOR模型的溯源对比实验，观察是否导致检测效率上的差异。令2个实验中感染概率p1相同，恢复概率q1与封禁概率o1一致，而对于概率p2与o2尽可能取值偏小，每组执行2000次模拟，实验结果如图6所示，可以看出，不论是JC或CC算法，SIOR模型的检测误差均低于SIR模型下的检测误差。所以加强对网络中传播谣言节点的检测能力，可以提高溯源效率。

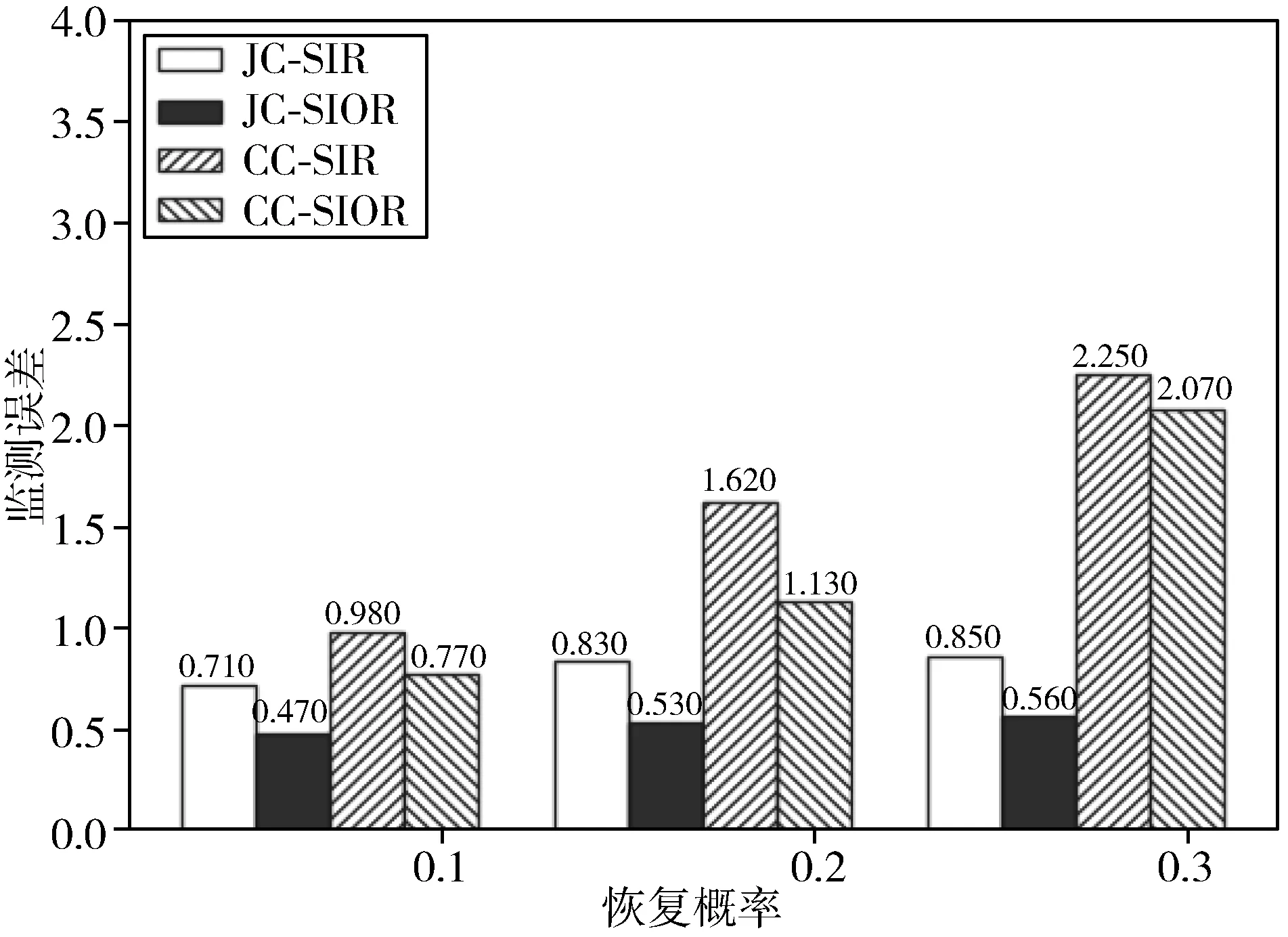
图6 2种模型的对比实验结果

5 结束语

本文基于SIR模型提出SIOR模型对谣言溯源进行研究，证明了在SIOR模型中，最优信息传播过程的起始节点可以作为源头的估计值，并且近似于拓扑结构中的Jordan感染中心。本文还提出了针对SIOR模型的反向信息传播算法，可以找出网络拓扑中的Jordan感染中心，即源节点的估计值。最后实验结果显示该溯源方法优于其他中心性溯源方法，且对于封禁隔离状态的加入，一定程度上有利于源头的检测。