基于故障树的水下生产系统可靠性分配
2022-02-12柳梦雪胡忠前肖文生
柳梦雪,刘 健,胡忠前,刘 超,肖文生
(1.中国石油大学(华东) 机电工程学院, 山东 青岛 266580; 2.海洋物探及勘探设备国家工程实验室,山东 青岛 266580; 3.中海油研究总院有限责任公司, 北京 100020)
随着陆上油气资源可开采量的持续降低,勘探开发海洋油气资源成为新的能源战略趋势[1]。水下生产系统一般包括水下控制系统、水下管汇、水下井口装置及采油树、海底管线和其他油气处理设施等。水下生产系统采出的油气资源通过立管回接到生产平台或生产储油轮上[2]。凭借经济性好、适用性强、安全性高等优势成为深水或超深水油气资源开发的主要模式[3]。其中,设备安全可靠运行是保证资源开发和保护生态环境的关键。
针对这一问题,充分考虑影响水下生产系统可靠性的各种因素,采用科学的决策方法对其进行可靠性分配,使系统设计更加合理,并从根本上保证可靠性。贾鹏[4]等采用基于重要度和复杂度的可靠性分配方法,完成了全电式水下生产系统阀门执行器的可靠性分配。冷伟[5]等采用改进的模糊层次分析法对常见的4类钢阀门进行可靠性分配,对水工钢阀门的结构设计具有一定的参考价值。苗利军[6]等以构造判断矩阵的拟优一致矩阵和群组层次分析法综合判断矩阵为基础,提出了一种基于改进层次分析法的电子对抗系统可靠性分配方法。石闯[7]等提出针对船舶操舵控制系统的评分分配法,对系统内单元的可靠性指标进行分配得出每个单元的可靠度指标,为优化系统的设计提供了可靠性依据。单一的可靠性分配方法具有一定的局限性,工作量大、主观性强且分配效率低。水下生产系统复杂程度比较高,需采用复合分配法对其进行可靠性分配[8]。
本文首先采用基于概率重要度的方法对故障树顶事件进行可靠性分配,然后利用可靠性再分配法对初级中间事件进行可靠性分配,最后采取层次分析法对故障率发生改变的次级中间事件进行可靠性分配。最终自上而下有层次的将系统可靠性指标分配到零部件上。
1 可靠性分配基础理论
可靠性分配是在系统设计阶段,将规定的可靠性指标按照一定的方法和原则合理分配给各个子系统及零部件,是一个自上而下、由整体到局部的演绎分解过程。可靠性分配作为可靠性设计的重要内容,本质就是一个工程决策问题,主要集中在初步设计阶段,并在后期不断进行优化[9]。
可靠性分配的实质就是求解不等式组:
(1)

可靠性分配通常遵循以下准则:重要程度、故障维修性、费用灵敏度、复杂程度、技术水平和环境条件[10]。
1) 重要程度。重要程度高的子系统应分配较高的可靠性指标,因为重要程度高的子系统故障会影响重要任务的完成甚至威胁人身安全。
2) 故障维修性。故障维修性差的子系统应分配较高的可靠性指标,因为故障维修性差的子系统需要耗费大量时间与资金。
3) 费用灵敏度。费用灵敏度高的子系统应分配较低的可靠性指标,因为子系统费用灵敏度高,提高相同可靠性所付出成本也高。
4) 复杂程度。复杂程度高的子系统应分配较低的可靠性指标,因为子系统复杂程度越高,提高其可靠性就越困难且成本越高。
5) 技术水平。技术水平成熟的子系统应分配较高的可靠性指标,因为子系统技术水平高,容易达到高可靠性值,且只需投入较少成本便可提高其可靠性。
6) 环境条件。环境条件恶劣的子系统应分配较低的可靠性指标,因为环境条件恶劣容易增加子系统的故障率。
2 基于故障树的水下生产系统可靠性分配模型
2.1 确定可靠性分配指标
可靠性分配指标通常选取为故障率、平均故障间隔时间、复杂度和重要度等[11]。本文选取最直接的判定指标—故障率作为可靠性分配指标,进行可靠性分配。
2.2 确定可靠性分配方法
基于故障树的可靠性分配方法主要有2种:基于最小割集或最小径集的可靠性分配;基于最小工作量的可靠性分配[12]。
对于水下生产系统这种复杂系统,每一个基本事件均为最小割集,逻辑关系较为简单,但最小割集数量过大,选用基于最小割集或最小径集的可靠性分配方法计算会降低分配效率;水下生产系统故障树每层事件较多,若选用基于最小工作量的可靠性分配方法只提高可靠性最低事件的可靠度,其他可靠性相对较低事件并没有得到改善,分配结果并非最优的。
水下生产系统故障树共分为4层:第1层为顶事件,第2层为初级中间事件,第3层为次级中间事件,第4层为三级中间事件。在基于故障树的水下生产系统可靠性分配中,首先将顶事件故障率分配到第2层,由于顶事件是系统最不希望发生的事,因此采用基于概率重要度的可靠性分配方法。第2层事件分配完成后,第3层事件的可靠性指标已不再满足新要求。由于次级中间事件数量过多,因此选用可靠性再分配的方法,为提高分配效率,只选择可靠性较低的事件进行分配。第4层事件涉及系统各类影响因素,选择层次分析法对其进行可靠性分配。最终自上而下有层次的将系统可靠性指标分配到零部件上[13]。
2.3 基于概率重要度的顶事件可靠性分配
事件概率重要度越高,改变其故障率对顶事件故障率的变化越明显、影响也越大,分配到的故障率也应该越小,因此在可靠性分配时应优先考虑。

Δq1∶Δq2∶…∶Δqi=I1∶I2∶…∶Ii
(2)
式中:Δq1为事件i经过分配后需要调整的概率值;Ii为事件i对组成事件的概率重要度。
此时,事件i分配后的概率为:
(3)
则:
(4)
通过式(2)~(4)可得Δqi,若Δqi>0,需降低该事件的可靠性,反之则需提高该事件的可靠性。
2.4 基于可靠性再分配法的初级中间事件可靠性分配
1) 根据故障树事件故障率从高到低进行排序。
P1>P2>…>Pk0>Pk0+1>…>Pn
2) 将故障率较高的P1,P2,…,Pk0降低到某一定值P0,Pk0+1,…,Pn保持不变。
此时顶事件故障率Ps为:
Ps=Φ(P1,P2,…,Pn)=1-(1-P0)k0×
(5)
式(1)转换为:
(6)
3) 确定k0和P0。
(7)
2.5 基于层次分析法的次级中间事件可靠性分配
1) 建立层次结构模型[14]。
目标层A为可靠性指标;准则层C为影响可靠性的各种因素,根据问题复杂程度可再次进行层次划分,且准则层的指标越多,目标层的可靠性越精确;方案层P为待分配对象及指标。
2) 选择标度并构造判断矩阵。
①选择标度。
建立层次结构模型之后,需要构造两两判断矩阵。为了量化各因素间的相对重要程度,需要选择一种定量判断的尺度。1~9标度是最常用的表示方法,具体含义如表1所示。

表1 1~9标度含义
②构造判断矩阵。
构造方案层相对准则层判断矩阵的具体方法为:首先从方案层任取两个元素ui和uj,比较二者对准则层的重要程度,记为aij,以此类推,直至将方案层全部元素两两比较,赋予相应的标度数值。由此得到判断矩阵A:
根据判断矩阵的构造原理,A具有以下性质:
aij>0;aij=1/aij;aij=1。其中i,j=1,2,…,n。
3) 计算准则层权重向量并进行一致性检验。
①计算判断矩阵最大特征根λmax及对应的特征向量ω。
②计算判断矩阵一致性指标C.I.。
(8)
式中:n为判断矩阵的阶数。
③查表2确定随机一致性指标R.I.。

表2 随机一致性指标
④计算判断矩阵一致性比例C.R.。
(9)
若C.R.<0.1,此矩阵通过一致性检验,特征向量ω即为权重向量;反之需要重新构造判断矩阵。
4) 计算权重向量。
(10)
5) 分配可靠性指标。
方案层中由k个对象构成的组成单元中第i个对象的故障率Pi为:
(11)
式中:P为顶事件允许的故障率。
3 算例
本文以乐东22-1南块气田作为研究对象,进行可靠性分配。
3.1 顶事件可靠性分配
由故障树定量分析计算得出初级中间事件故障率及初级中间事件对顶事件的概率重要度,如表3所示。

表3 事件故障率和概率重要度
由故障树定性分析得到水下生产系统故障率为775×10-6h-1,希望设计的生产系统的故障率能够
降到500×10-6h-1,因此,重新分配事件M1、M2、M3、M4、M5的故障率,联立方程组:
(12)
利用MATLAB进行求解计算,结果如表4和图1所示。

表4 顶事件分配结果对比
从图1可以看出事件M1和M4故障率比较高,因此只改变事件M1和M4故障率,其余事件故障率保持不变。

图1 顶事件分配结果对比
3.2 初级中间事件可靠性分配
完成顶事件可靠性分配后,部分初级中间事件现有故障率已经不符合要求。因此,采用可靠性再分配方法对初级中间事件进行分配,以事件M1为例说明具体分配过程。
1) 事件M1的下层事件及其故障率。
PN2=68.35×10-6、PN3=13.96×10-6、
PN4=35.6×10-6、PN5=26.82×10-6、
PN6=245×10-6
所以:PN6>PN2>PN4>PN5>PN3
2) 事件M1分配后的故障率为335×10-6h-1。根据式(5),调整后的事件M1与下层事件N2、N3、N4、N5、N6的关系为:
采取试错法[15]来得到k0和P0,计算过程如下:
① 当k0=1时。
Ps=1-(1-P0)(1-PN2)(1-PN3)(1-PN4)×
(1-PN5)
=190.29×10-6 ② 当k0=2时。 Ps=1-(1-P0)2(1-PN3)(1-PN4)(1-PN5) =129.23×10-6>PN2 因此,k0=2不满足条件,k0取1,即只改变事件N6的故障率。将事件N6的故障率降为190.29×10-6h-1,事件N2、N3、N4、N5的故障率仍为原值。 采用同样的方法对事件M4进行可靠性再分配,结果如表5和图2所示。 表5 初级中间事件分配结果对比 续表5 图2 初级中间事件分配结果对比 由图2可知,通过可靠性再分配法筛选出故障率较高的次级中间事件N6和N18,其余故障率较低的事件保持不变。 完成初级中间事件可靠性分配后,需要重新分配故障率发生变化的初级中间事件对应的次级中间事件。采用层次分析法进行可靠性分配: 1) 选取重要程度、故障频繁性、故障危害性和费用灵敏度为准则层影响因素。影响因素集和次级中间事件的层次结构模型如图3所示。 ①重要程度。主要考虑次级中间事件的概率重要度,与可靠度成正比。 ②故障频繁性。根据故障树模型可以计算各个事件的发生频率,与可靠度成反比。 ③故障危害性。表现为组成单元发生故障时对系统造成的危害程度,与可靠度成正比。 ④费用灵敏度。投入单元费用所提高的可靠性程度,与可靠度成反比。 图3 次级中间事件层次结构图 2) 构造准则层影响因素重要程度、故障频繁性、故障危害性和费用灵敏度对目标层的判断矩阵A。 3) 检验判断矩阵一致性并计算准则层对目标层权重向量。 ①利用MATLAB计算出判断矩阵A的最大特征根及对应的特征向量。 λmax=4.031 0,ω=(0.482 6,0.813 5,0.278 7,0.166 1)T ②由式(8)计算一致性指标C.I.。 ③确定随机一致性指标R.I.。 由表2得随机一致性指标R.I.为0.90。 ④由式(9)计算一致性比例C.R.。 因此,判断矩阵一致性程度可以接受,归一化后准则层权重向量为ω=(0.277 2,0.467 3,0.160 1,0.095 4)T。 4) 计算方案层对准则层权重向量。 由故障树定量分析可以计算出次级中间事件的发生概率和概率重要度,因此可以直接得出事件在故障频繁性和重要程度下的两两判断矩阵,通过专家评分的方法得出次级中间事件在故障危害性和费用灵敏度下的判断矩阵。 以事件N18为例计算方案层对准则层权重向量。事件N18包括3个下层事件P34、P35和P36。 ① 事件N18在影响因素“重要程度”下的判断矩阵。 ω=(0.333 3,0.333 3,0.333 3)T ②事件N18在影响因素“故障频繁性”下的判断矩阵。 ω=(0.320 4,0.379 6,0.300 9)T ③事件N18在影响因素“故障危害性”下的判断矩阵。 ω=(0.136 5,0.238 5,0.625 0)T ④事件N18在影响因素“费用灵敏度”下的判断矩阵。 ω=(0.163 5,0.539 6,0.296 9)T 由式(10)得事件P34、P35、P36在全部影响因素下的权重为: ωP34=(0.277 2,0.467 3,0.160 1,0.095 4)× (0.333 3,0.320 4,0.136 5,0.163 5)T =0.279 5 ωP35=(0.277 2,0.467 3,0.160 1,0.095 4)× (0.333 3,0.379 6,0.238 5,0.539 6)T =0.359 4 ωP36=(0.277 2,0.467 3,0.160 1,0.095 4)× (0.333 3,0.300 9,0.625 0,0.296 9)T =0.361 因此事件N18在全部影响因素下的权重为:ωN18=(0.279 5,0.359 4,0.361 )T,以此类推得事件N6的权重为: ωN6=(0.059 4,0.474 2,0.104 4,0.361 9)T 5) 分配可靠性指标。 由式(11)进行次级中间事件的可靠性分配,以事件N18为例: 此时: 同理可得事件X1、X2、X3、X4分配后的故障率,如表6和图4所示。 表6 次级中间事件分配结果对比 图4 次级中间事件分配结果对比 本文针对水下生产系统结构复杂这一问题,提出一种基于概率重要度、可靠性再分配法和层次分析法的复合分配法,建立水下生产系统可靠性分配模型,依次完成顶事件、初级中间事件和次级中间事件的可靠性分配,并以乐东22-1南块气田为例验证了该方法的可行性和准确性。 确定故障率较高的薄弱环节,即对主控站、液压动力单元、采油树节流模块结构装置、采油树节流模块耦合器、化学注入单元和电力单元进行改进和优化,为后续水下生产系统可靠性设计提供参考。


3.3 次级中间事件可靠性分配

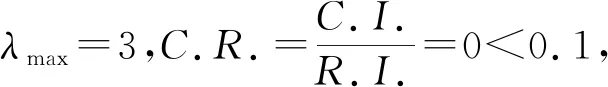
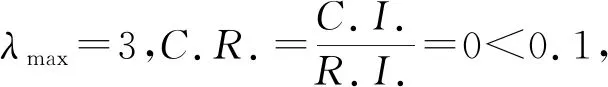

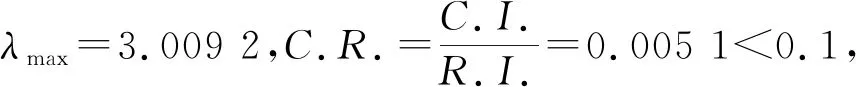


4 结语
