Subgradient Extragradient Methods for Equilibrium Problems and Fixed Point Problems in Hilbert Space

Lulu Yin and Hongwei Liu

(School of Mathematics and Statistics, Xidian University, Xi′an 710126, China)

Abstract: Inspired by inertial methods and extragradient algorithms, two algorithms were proposed to investigate fixed point problem of quasinonexpansive mapping and pseudomonotone equilibrium problem in this study. In order to enhance the speed of the convergence and reduce computational cost, the algorithms used a new step size and a cutting hyperplane. The first algorithm was proved to be weak convergence, while the second algorithm used a modified version of Halpern iteration to obtain strong convergence. Finally, numerical experiments on several specific problems and comparisons with other algorithms verified the superiority of the proposed algorithms.

Keywords: subgradient extragradient methods; inertial methods; pseudomonotone equilibrium problems; fixed point problems; Lipschitz-type condition

0 Introduction

(1)

which is also called Ky Fan inequality[1]. Here, its disaggregation is denoted by EP(X,f).Interestingly, fixed point problem, Nash equilibrium problem, variational inequality, optimization problem, and many other models can be transformed into EP[2-4]. In recent years, numerous measures of seeking the approximate solution of problem (1) have been discussed[5-12].

A common measure is extragradient method[7-8], which tackles two strongly convex programming models in every iteration. Evaluation of the subprograms of the algorithm may be extremely expensive for involute structure of bifunctions and/or feasible sets. In recent years, there is a vast amount of literature concerning the study and improvement of this algorithm, among which Refs. [9-13] are representative. To combat this drawback, Van Hieu[10]put forward an modified way to settle fixed point problem and equilibrium problem by using Halpern iteration method and subgradient extragradient, and established the strong convergence result. It is clear that the second strongly convex programming problems is performed in half space. Furthermore, to speed up the convergence of the algorithm, Rehman et al.[14]recently designed a new algorithm by applying the inertial technique[15-17], and obtained the weak convergence results under appropriate assumptions.

Motivated and inspired by the several above-mentioned advantages in Refs.[10] and [14], this paper introduces two new algorithms to analyze fixed point problem with quasinonexpansive mapping and pseudomonotone equilibrium problem. Moreover, the weak convergence results of one algorithm and the strong convergence results of another algorithm were obtained. Among the two proposed algorithms, the new step size avoids Lipschitz constants of bifunction. The experimental results reflect the numerical behavior.

The paper is structured as follows. Some preliminary information is reviewed in Section 1. Section 2 is the research of the convergence results. The similar application to variational inequalities is elaborated in Section 3. Eventually, two experiments of Section 4 show that the proposed algorithms possess perfect efficiency.

1 Preliminaries

In this paper, several notations and lemmas were introduced for later use. Stipulates+=max{0,s},s-=max{0,-s}, ∀s∈R.Presume thata,b,c∈Handτ∈Rare known. Then

‖τb+(1-τ)c‖2=τ‖b‖2+(1-τ)‖c‖2-

τ(1-τ)‖c-b‖2

(2)

2〈b-c,b-a〉=‖b-c‖2+‖a-b‖2-

‖c-a‖2

(3)

Evidently,the projectionPXpossesses the following feature:

c=PXb⟺ 〈b-c,a-c〉≤0, ∀a∈X

Definition1.1Bifunctionf:H×H→Ris

• Pseudomonotone inX:

f(b,c)≥0 ⟹f(c,b)≤0, ∀a,b∈X

• Lipschitz-type condition inX:

Further, givenc∈Xand functionh:X→(-∞,∞], its subdifferential is described by

∂h(c)={ξ∈H:h(b)-h(c)≥

〈ξ,b-c〉, ∀b∈X}

and its normal cone ofXis

NX(c)={η∈H∶〈η,b-c〉≤0,b∈X}

Lemma1.1[18]Supposeh:X→(-∞,+∞] is subdifferentiable, lower hemicontinuous, and convex. Suppose that there is a point onXthat makeshcontinuous, orhis finite at some interior point onX.Thenc*=arg min{h(c):c∈X} is equivalent to 0∈∂h(c*)+NX(c*).

Definition1.2Fix (T)≠∅ andT:H→Hare known, then

1)Tis known as quasi-nonexpansive:

∀a∈H,b∈Fix(T),‖Ta-b‖≤‖a-b‖

2)T-Iis known as demiclosed at zero:

∀{cn}⊂H, s.t.cn⇀z,

Tcn-cn→0 ⟹c∈Fix(T)

The information of the proximal operator is recalled which is the basic tool for the proposed algorithm. Assume that a functionh:H→(-∞,∞] is lower hemicontinuous, proper, and convex. Givenλ>0 andc∈H, the proximal operator ofhis described as

Then a crucial attribute of proximal operators is recommended.

Lemma1.2[19]Letc∈H,b∈X, andλ>0.Then

(4)

Lemma1.3(Peter-Paul inequality) Givenε>0 anda1,a2∈R, the following property holds:

(5)

Lemma1.4(Opial) Given progression {cn}⊂H, supposecn⇀c.Then

(6)

Lemma1.5[16]Sequences {ϑn}, {αn}, and {ιn} in [0,+∞) satisfy

Suppose that real numberαexists and has 0≤αn≤α<1, ∀n∈N.Thus, the following can be obtained:

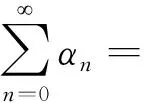
2 Algorithms and Convergence Analysis

Two methods are proposed and studied in this section. To prove the algorithm’s convergence, the following assumptions are proposed.

Condition (A):

(A1)fis pseudomonotone overX;

(A2)f(z,·) has convexity and subdifferentiability overXfor anyz∈H;

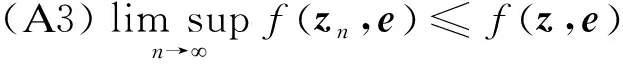
(A4)fhas Lipschitz-type condition overHwithl1,l2>0.

Remark2.1It is explicit when Condition (A) is satisfied. The EP(f) of problem (1) is convex and closed[7, 10]. In addition, Fix(T)⊂His also convex and closed under the condition thatTis quasi-nonexpansive[21]. Moreover, the symbolΛ=EP(X,f)∩Fix(T) is taken for convenience.

2.1 Weak Convergence

First,inspired by the works of Ref.[14], the algorithm’s weak convergence is derived. In addition, the algorithm’s step size is specially selected, which makes it unnecessary for the algorithm to know Lipschitz constants in advance. The first algorithm has the following form:

Algorithm2.1

Step1Assume thatxn-1andxnare known. Compute

wn=xn+αn(xn-xn-1)

Step2Selectvn∈∂2f(wn,yn) such that

wn-λnvn-yn∈NX(yn)

Compute

where

Tn={x∈H:〈wn-λnvn-yn,yn-x〉≥0}

Step3Definexn+1=(1-βn)wn+βnTznand

λn+1=

Ifwn=yn=xn+1, then stop,wn∈Λ.

Taken: =n+1 and revert to Step 1.

Remark2.2It is easy to confirm the existence ofvnandX⊂Tnfrom Algorithm 2.1. Please refer to Ref.[22] for detailed proof.

Remark2.3The existence of the parameterμin Algorithm 2.1 is necessary for the subsequent proof that the proposed algorithm is convergent.

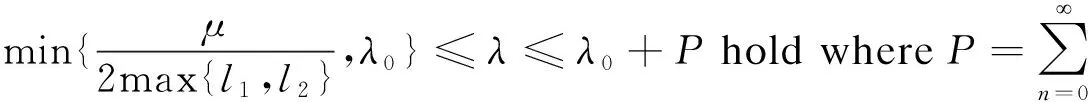
ProofWhen

f(wn,zn)-f(wn,yn)-f(yn,zn)>0

the Lipschitz condition offis engendered:

Using the above inequality and induction, it is obvious that the following expression can be derived:

Takingsn+1=λn+1-λn, definition of {λn} leads to

(7)

(8)

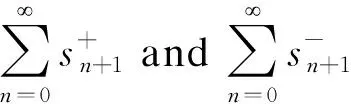
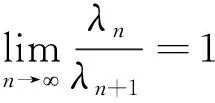
Now, a lemma is introduced to pave the way for proof of convergence result.

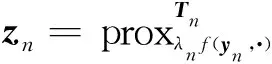
λn(f(yn,z)-f(yn,zn))≥

〈wn-zn,z-zn〉, ∀z∈Tn

(9)

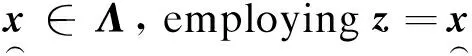
(10)

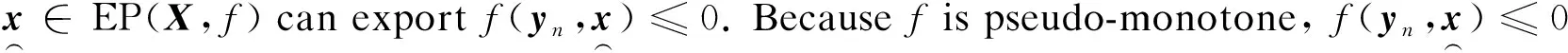
(11)

Using the concept of the subdifferential,zn∈Tn⊂Handvn∈∂2f(wn,yn), the following expression is derived:

f(wn,zn)-f(wn,yn)≥〈vn,zn-yn〉

(12)

Owing to the given form ofTn, it is found that

〈wn-λnvn-yn,zn-yn〉≤ 0

Hence, there is

λn(f(wn,zn)-f(wn,yn))≥〈yn-wn,yn-zn〉

(13)

Applying inequalities (11) and (13) yields

2λn(f(wn,zn)-f(wn,yn)-f(yn,zn))≥2〈yn-

(14)

Through the representation ofλn, the following is achieved:

(15)

Lemma2.3Algorithm 2.1 formulates progressions {xn}, {wn}, and {yn}.Suppose

If the sequence {xnk} tox″∈His weakly convergent, thenx″∈Λ.

ProofApparently, there iswnk⇀x″,ynk⇀x″,znk⇀x″, andx″∈X.From the relation of Eq.(8), the following expression is deduced:

λnk(f(ynk,z)-f(ynk,znk))≥

〈wnk-znk,z-znk〉, ∀z∈Tn

(16)

The Lipschitz-type condition offonXyields

λnkf(ynk,znk)≥λnk(f(wnk,znk)-f(wnk,ynk)) -

λnkl1‖ynk-wnk‖2-λnkl2‖ynk-znk‖2

(17)

According to inequalities (13) and (17), the following expression can be obtained:

λnkf(ynk,znk)≥〈wnk-ynk,znk-ynk〉-

λnkl1‖ynk-wnk‖2-λnkl2‖ynk-znk‖2

(18)

Combining inequalities (17) and (18), andX⊂Tn, it can be deduced for allz∈Xthat

l1‖ynk-wnk‖2-l2‖ynk-znk‖2

Taking the limit in the last inequality and using

f(x″,z)≥0, ∀z∈Xis deduced from the assumption (A3). In other words,x″∈EP(X,f).Moreover, sinceznk⇀x″ and demiclosedness of zero ofI-T,x″∈Fix(T) is discovered. Then,x″∈Λ.

(19)

By invoking quasi-nonexpansion ofT,βn≤1/2 andxn+1=(1-βn)wn+βnTzn, the following expression is obtained:

(20)

Furthermore,by utilizing the definition ofwnand inequality (2), it is derived

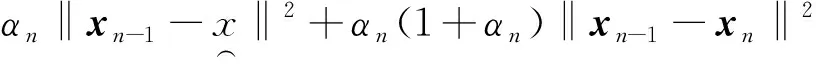
(21)

and

2αn〈xn-1-xn,xn-xn+1〉≥‖xn-xn+1‖2+

‖xn-1-xn‖)=(1-αn)‖xn-xn+1‖2-

(22)

Applying inequalities (20), (22), and Eq. (21), the following expression can be deduced:

(1-αn)‖xn-xn+1‖2

(23)

The non-decreasing property of {αn} leads to

αn)‖xn-xn+1‖2+2αn‖xn-1-xn‖2

(24)

Let

2αn‖xn-1-xn‖2

then (23) is equivalent to

ιn+1-ιn≤(2αn+1-1+αn)‖xn-xn+1‖2

(25)

2αn+1-1+αn≤3α-1<0

In inequality (25), -ϑ=3α-1 leads to

0≥-ϑ‖xn-xn+1‖2≥ιn+1-ιn

(26)

In other words, progression {ιn} does not increase. Moreover, utilizing the form ofιn, the following expression is deduced:

(27)

Also,considering the form ofιn+1, the following formula is obtained:

(28)

Hence, inequalities (27) and (28) indicate that

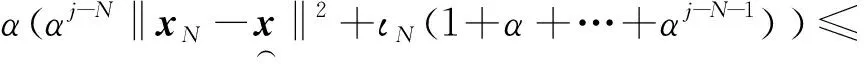
(29)

By making use of inequalities (26) and (29), there is

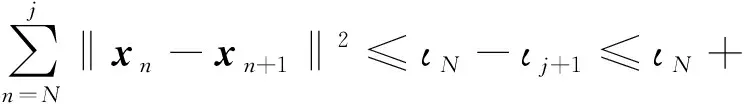
(30)

Setk→∞ from inequality (30), the following expression is derived:

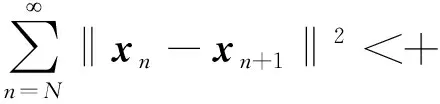
(31)

which indicates

(32)

By usingαn≤α, there is

‖wn-xn+1‖≤‖xn-xn+1‖+αn‖xn-1-xn‖≤

‖xn-xn+1‖+α‖xn-1-xn‖

(33)

Therefore, by Eq.(32) and inequality (33), the following expression is obtained:

(34)

Combining Eqs.(32) and (34) yields

‖wn-xn+1‖)=0

So

(35)

From expression (22), forn≥N, the following expression is obtained:

(36)

By inequality(31) and (36), and invoking Lemma 1.5, there is

‖xn-x′‖2→σ

(37)

Eq.(35) leads to

‖wn-x′‖2→σ

(38)

Because of the relationship provided in inequality (20), the following is obtained:

which means

(39)

Exploiting Lemma 2.2, the following expression is derived:

Therefore,

(40)

Lemma 2.2 is invoked to obtain

The last expression implies that

So it is found that

there is

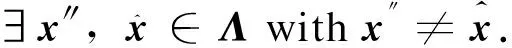
(41)

Applying Lemma 1.4, it is deduced that

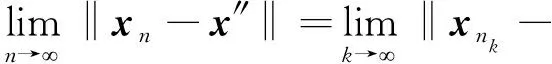
(42)

There is a contradiction in Eq.(42). As a result,xn⇀x″.Given

there isyn⇀x″ andzn⇀x″.

2.2 Strong Convergence

In this framework, inspired by Refs.[10], [12] and [23], Algorithm 2.1 was improved by using the modified version of Halpern iteration. To study the algorithhm’s strong convergence, some assumptions are added.

Condition (B):

(B2)γn∈[a,b]⊂(0,1);

Next, the form of algorithm is described in detail.

Algorithm2.2

Step2Takewn=xn-αn(xn-1-xn) and calculate

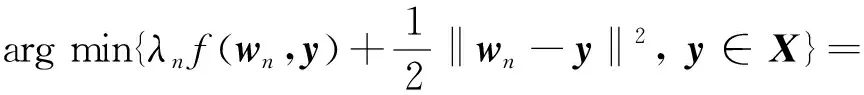
Step3Pickvn∈∂2f(wn,yn) such thatwn-λnvn-yn∈NX(yn)

compute

where

Tn={x∈H|〈wn-λnvn-yn,yn-x〉≥0}

Step4Formulate

xn+1=γnT(βnx0+(1-βn)zn)+(1-γn)xn

and

λn+1=

Taken: =n+1 and transfer to Step 1.

Remark2.2Apparently, it holds that

Actually, the following expression can be easily obtained:

αn‖xn-xn-1‖≤εn

From the above formula and hypothesis (B3), it is directly deduced that

ProofPlease refer to Refs.[12] and [22] for the detailed proof of the theorem.

3 Research on Variational Inequalities

(43)

where VI(X,F) represents the disaggregation of problem (43). HereFis called

• pseudo-monotone overX:

〈F(d),e-d〉≥0⟹〈F(e),e-d〉≥0, ∀d,e∈X

•L-Lipschitz continuous overX:

∃L>0, s.t. ‖F(d)-F(e)‖≤L‖d-e‖, ∀d,e∈X

Make the following presumptions about VIP:

(B1)Fis pseudo-monotone overX;

(B2)Fis weakly sequentially continuous overXfor any progression {zn}∶{zn} weakly converging toz, which means {F(zn)} weakly converges toF(z).

(B3)FpossessL-Lipschitz successive overX.

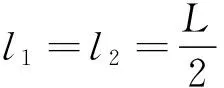
Similarly,znin the proposed algorithms reduces to

zn=PTn(wn-λnF(yn))

Firstly, the following conclusions are obtained by observing the proof about Algorithm 2 for Ref. [23].

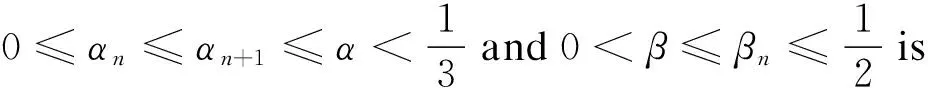
dn=xn-αn(xn-1-xn)

yn=PX(dn-λnF(dn))

zn=PTn(dn-λnF(yn))

Tn={x∈H|〈λnF(dn)+yn-dn,yn-x〉≤0}

xn+1=(1-βn)dn+βnTzn

Then progression {xn} weakly converges to a certain spot of Fix(T)∩VI(X,F).

Then, a strong convergence schemeis presented. Its proof is similar to that in Ref.[24] and is thus omitted.

dn=xn-αn(xn-1-xn)

yn=PX(dn-λnF(wn))

zn=PTn(dn-λnF(yn))

Tn={x∈H|〈λnF(dn)+yn-dn,yn-x〉≤0}

xn+1=(1-γn)zn+γnT((1-βn)zn+βnx0)

λn+1=

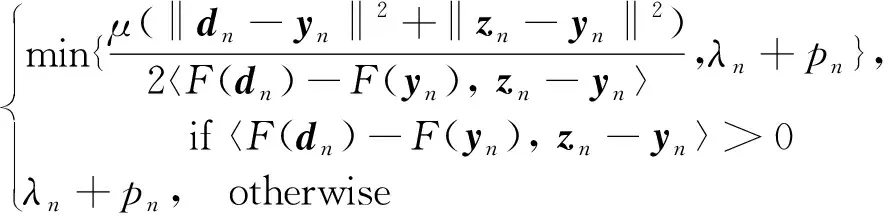
Then progression {xn} strongly converges to a dotx′, wherex′∈PFix(T)∩VI(X,F)(x0).

Remark3.1For convenience, the algorithms proposed by Theorem 3.1 and Theorem 3.2 are denoted as Algorithm 3.1 and Algorithm 3.2, respectively. They are direct applications of Algorithm 2.1 and Algorithm 2.2 to variational inequalities. Moreover, it is worth noting that the formula of calculating shadow onto a closed convex setTn[25]is stated as

wheree=wn-λnF(wn)-ynandx=yn.

4 Numerical Experiments

The proposed algorithms are compared with other algorithms in numerical experiments, and their effectiveness is illustrated in this section. For Algorithm 2.1 and Algorithm 3.1, takeμ=0.6,λ1=0.12,αn=0.32,βn=0.5, andpn=1/(n+1)10.For all the tests, record the number of iterations (Iter.) and calculation time (Time) implemented in the passing seconds. Particularly, ‖xn-xn+1‖≤εandε=10-3are adopted as terminate principle.

ProblemIThe first experiment is focused on equilibrium problem.f:H×H→Ris known and makef(y,z)=〈z-y,Ky+Mz+d〉 hold. Each item ofd∈Rmis casually created from [-5, 5]. It holds thatMandK-Mare symmetric positive semi-definite matrices ofm×m.The practicable set is

X={x∈Rm:-2≤xi≤2,i=1,…,m}

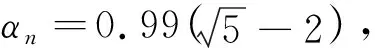
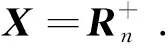
Table 1 Numerical results of problem I with starting dot (1,1,...,1)

In conclusion, compared with Algorithm 3.1 of Ref.[27] and Algorithm 4.3 of Ref.[28], this algorithm has better performance.

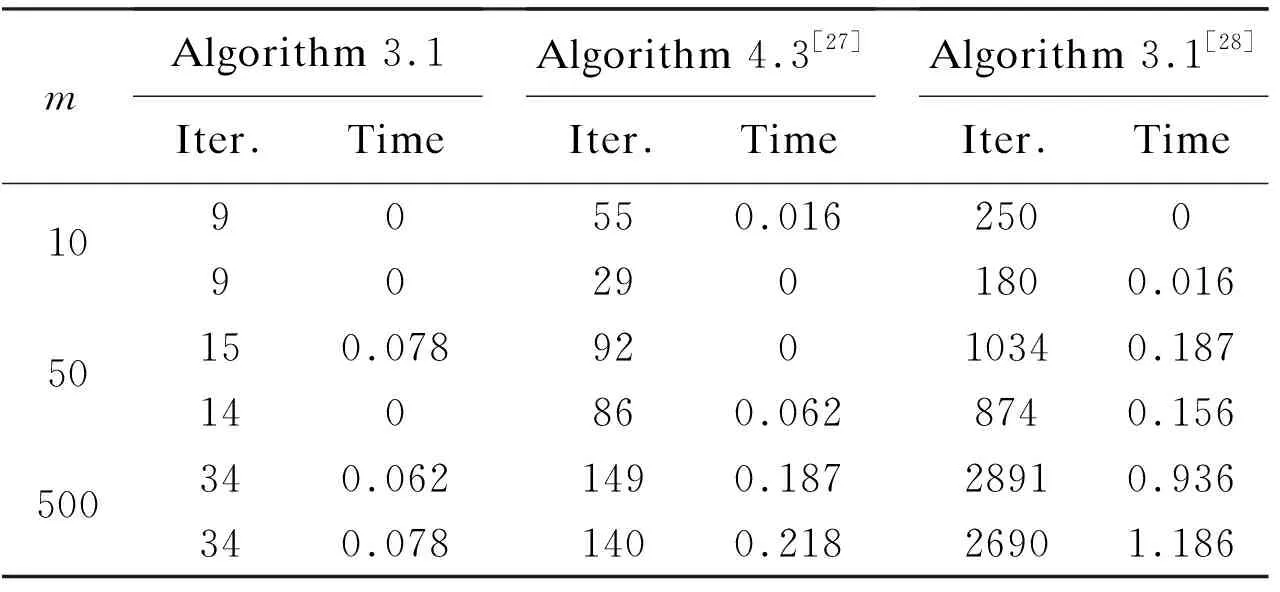
Table 2 Numerical results of problem II with starting dot (1,1,...,1)

5 Conclusions

With regard to the fixed point problem and equilibrium problem, two new algorithms were proposed. Under appropriate circumstances, the convergence of algorithms was discussed. In particular, the variational inequalities were also studied. The performance of the proposed algorithms was demonstrated by observing the numerical results, which shows that the algorithms are effective.