双肢冷弯C型钢蒙古包刚架的平面内稳定性

陈 明 ，鲁卫波 ，武志远 ，李补拴

（内蒙古科技大学土木工程学院, 内蒙古 包头 014010）

近年来，草原地区居民对房屋建筑的使用要求不断提升，能够实现大跨度高承载能力的蒙古族特色建筑成为应用研究热点.用冷弯型钢构建的新型蒙古包结构应运而生，其主要承力的带陶脑的门式刚架是该结构在草原典型风雪荷载作用下安全使用的根本保证，但还缺乏此类研究.

当前，国内外学者对门式刚架已展开了较为广泛的研究.Davies[1]进行了等截面门式刚架的试验研究与理论分析，使用参考能量法推导出了相对复杂的门式刚架稳定极限承载力公式.Baigent和Hancock[2]对7组山形门式刚架进行不同荷载模式和侧向约束的试验，验证了将截面畸变纳入理论计算的可行性.Zhang等[3-5]提出了基于直接强度法和直接设计法的冷弯型钢门式刚架设计方法，并进行了一系列大跨度冷弯型钢门式刚架在考虑重力和侧向荷载下的全尺寸试验，结果表明，此类门式刚架的破坏以弯扭屈曲为主，采用直接强度法对门式刚架的极限承载力计算与实际有较大的差异.刘朝宏等[6-7]针对刚架的稳定问题进行了有限元研究，给出了考虑主弯矩对承载力影响的稳定计算公式.卢林枫等[8]通过梁弹簧单元模拟刚架的初始缺陷进行分析发现，节点板厚度、斜梁坡度、柱脚刚度是影响刚架承载力的重要参数.王万祯等[9]通过引入连接转动刚度和偏心支撑得到了偏心支撑半刚接刚框架柱的计算长度理论公式.陈明等[10-11]提出装配式冷弯C型钢蒙古包结构，并对带垫板的双肢冷弯C型钢门式刚架的节点进行了试验及理论分析，验证了此类节点连接的半刚性特征及可靠的承载能力.

规范[12]中门式刚架的计算长度系数是在忽略梁的轴力下按照侧移失稳的特征值方法求得的，在斜梁轴力大等特殊情况下，实际结果与传统计算有较大的差异.因此，考虑到研究现状和相关规范对门式刚架的分析计算，本文对所构建的新型结构采用试验、有限元及计算理论的多方面分析，探究其失稳破坏形态，得到其稳定极限承载力计算方法.

1 双肢冷弯C型钢门式刚架平面内稳定性能分析

1.1 刚架试件设计

为了满足试验要求，按照1/4相似比对带陶脑的双肢冷弯C型钢平面刚架的构件及节点进行设计，刚架跨度为3 m，梁柱构件截面均为带垫板的双肢 C 型钢，柱截面为 2C160 mm × 60 mm × 20 mm ×2.5 mm，梁截面为 2C120 mm × 50 mm × 20 mm ×2.5 mm.每个刚架试件的8根双肢C型钢均由梁填板、柱填板、梁柱节点板和柱脚连接板各2块连接；中间陶脑环直径为300 mm，连接板件壁厚均为10 mm；上述连接都采用10.9级M14摩擦型高强螺栓，柱底板与基础的连接采用10.9级M20摩擦型高强螺栓，试验试件其他参数见表1，为了验证有限元模型，同步进行了相应刚架的有限元分析.以CJ-BASE为例，刚架设计如图1所示.

图1 试件 CJ-BASE 设计及尺寸Fig.1 Design and dimensions of specimen CJ-BASE

表1 刚架试件设计参数Tab.1 Design parameters of rigid frames

1.2 有限元模型建立、网格划分和约束条件

本文采用Solidwork建模再导入Workbench软件进行有限元分析.刚架模型按照试验试件建立，梁柱构件采用实体单元 SOLID185，接触单元采用TARGE170模拟，摩擦系数取0.3.有限元构件采用Structural Steel材料，材料属性按材性试验结果（表2）输入，选用双折线本构模型.各材性试件的应力应变曲线见图2.网格划分采用局部和整体划分形式，如图3所示.

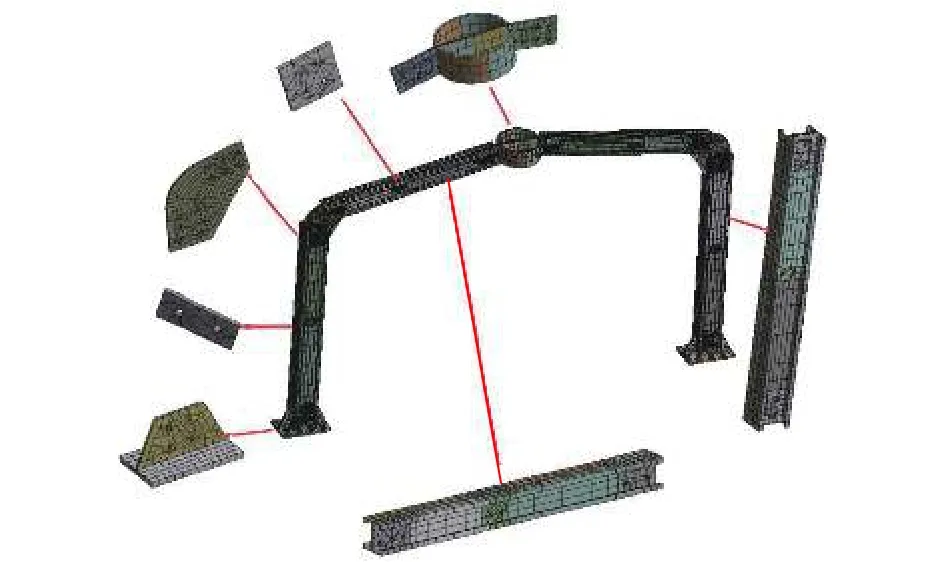
图3 试件 CJ-BASE 有限元模型Fig.3 Finite element model of specimen CJ-BASE

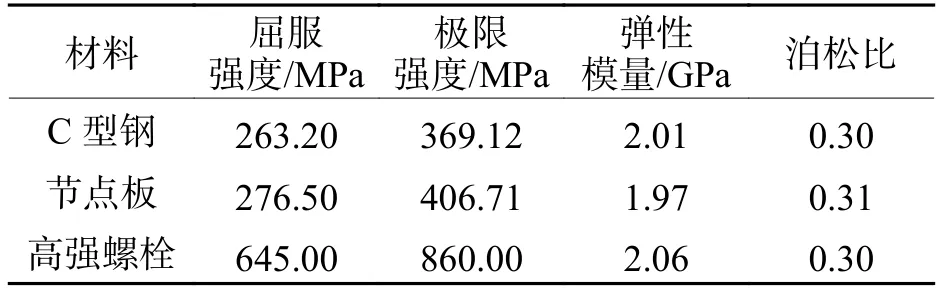
表2 钢材的材料性能参数Tab.2 Material behavior of steel

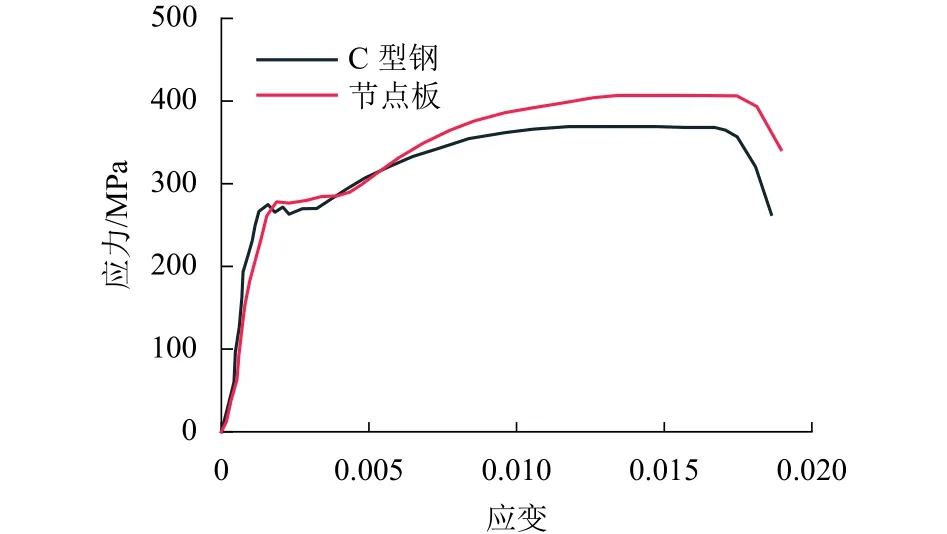
图2 材性试件的应力-应变曲线Fig.2 Stress-strain curves of specimen materials

对刚架两侧柱脚底板节点3个方向的自由度进行约束以模拟固结边界条件，同时限制两侧梁柱节点板及梁、柱填板节点Z方向位移，实现侧向约束，以防止刚架发生平面外失稳情况.

1.3 加载装置及加载制度

刚架加载装置如图4所示.通过500 kN千斤顶对两级分配梁施加竖向荷载，两级分配梁向下传递至斜梁中点和靠近陶脑处，形成四点加载方式.试件的承载力未考虑两级分配梁的自重.

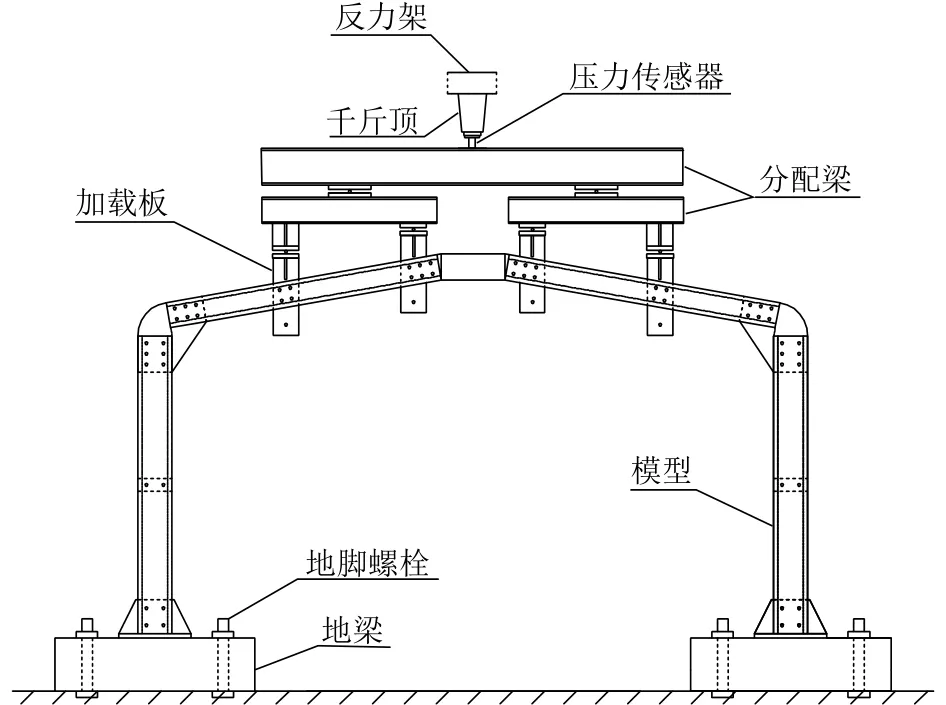
图4 模型及加载装置Fig.4 The model and loading device

刚架荷载施加分为两部分：先逐级施加预估极限位移的2%，当试件开始出现局部屈曲或者施加位移达到预估极限位移的80%时，按预估极限荷载的1%继续施加；当刚架试件中的某一构件发生严重破坏，或刚架出现整体失稳时结束加载.为防止刚架发生平面外失稳，在试验和有限元分析中设置侧向支撑和限制侧向位移的措施.有限元分析加载过程分为两个阶段：第一阶段，施加螺栓预紧力；第二阶段，在斜梁加载处直接施加位移荷载.

1.4 试验结果分析及有限元模型验证

对比试验和有限元分析结果可知：加载前期，刚架梁柱节点出现轻微螺栓滑移，随后出现塑性铰；随着加载位移增大，靠近梁柱节点和陶脑的斜梁先后出现局部屈曲，继而发展为畸变屈曲，所有试件均为斜梁的局部失稳导致刚架发生S形挠曲整体失稳，且呈现对称失稳形态.加载过程中，各试件的刚架柱仅产生了不同程度的柱顶平面内侧向位移，未进入塑性阶段，加载完毕后，刚架变形发生部分回弹，说明整体刚架并未全部进入塑性状态或仍处于弹塑性状态.

表3为各刚架试件的柱顶最大侧移值.由表3可知：斜梁坡度的增加，使刚架稳定承载力得到提高的同时，斜梁轴力导致其柱顶侧移值相应增加.这是由于斜梁坡度的增加，刚架产生了不同程度的拱效应，斜梁轴力的增大使柱顶侧移增大.规范[12]规定柱顶侧移限值为H/180 （H为刚架柱高度），所有试件中，只有试件CJ-2超出规范限制.

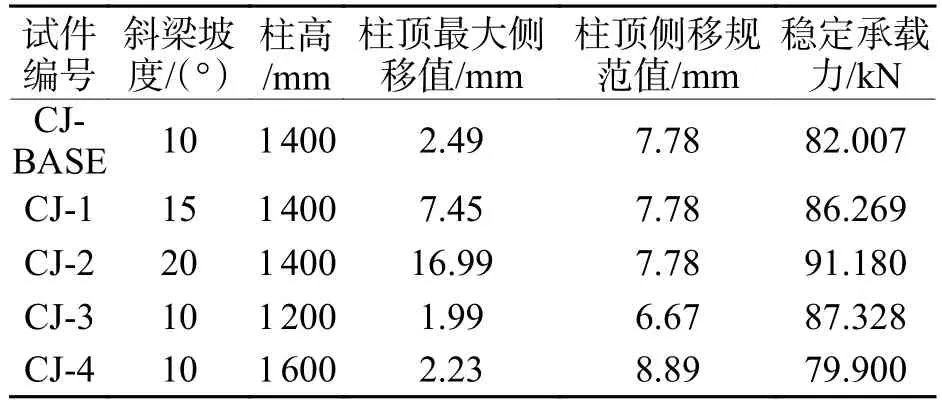
表3 刚架试件柱顶最大侧移值Tab.3 Maximum lateral displacement of column top of rigid frames

图5为试验与有限元的破坏形态，图6为试验荷载-位移曲线对比.从图5和图6的对比结果来看：有限元模型与试验试件破坏特征基本吻合；荷载-位移曲线的形状、极限荷载基本一致，验证了有限元模型及分析方法的准确性.由于试验时刚架节点处发生轻微的螺栓滑移，导致试验的荷载-位移曲线出现波折段.

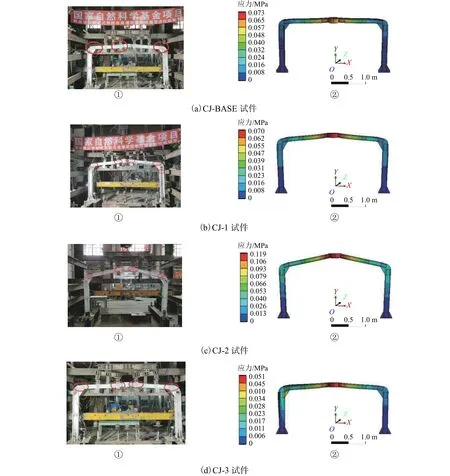
图5 各试件破坏形态对比Fig.5 Comparison of failure modes of specimens

图6 各试件荷载-位移曲线对比Fig.6 Comparison of load-displacement curves of specimens

2 冷弯C型钢刚架平面内稳定性参数分析

参数分析模型参考双肢冷弯薄壁C型钢蒙古包刚架部品库[11]中的实际尺寸来选取尺寸，建立有限元模型.本文将以斜梁坡度（HSR）、刚架高跨比（RS）、陶脑直径（TN）作为研究参数，以跨度为 12000 mm、檐口高度为 5600 mm、斜梁坡度为 10°、陶脑直径为1200 mm的模型PF-BASE作为分析的基准模型，其中柱 C 型钢截面尺寸为 2C300 mm × 90 mm ×25 mm × 3 mm、梁 C 型钢尺寸为 2C250 mm × 80 mm ×25 mm × 2.5 mm.一共进行了 13 榀足尺的带套脑双肢冷弯型钢蒙古包刚架在跨中竖向荷载作用下的模拟分析.

2.1 斜梁坡度

在基准模型PF-BASE的基础上，仅改变模型的斜梁坡度，其他参数保持不变.模型的具体参数和有限元分析结果见表4，荷载-位移曲线见图7.

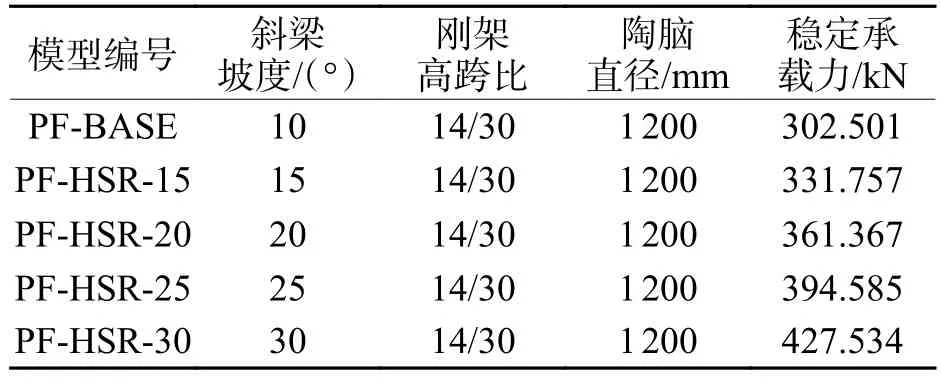
表4 不同斜梁坡度下模型有限元分析结果Tab.4 Finite element analysis results of models with different inclined beam slopes

由表4和图7所知：通过增加斜梁坡度可显著提高门式刚架的稳定承载力；相比斜梁坡度为10°的基准模型 PF-BASE，斜梁坡度增大至 15°、20°、25°、30° 时，门式刚架的稳定承载力分别增加了9.7%、19.5%、30.4%、41.3%；斜梁坡度的增加使斜梁的轴力增大，产生拱效应，其稳定承载力在一定程度上得到提高.

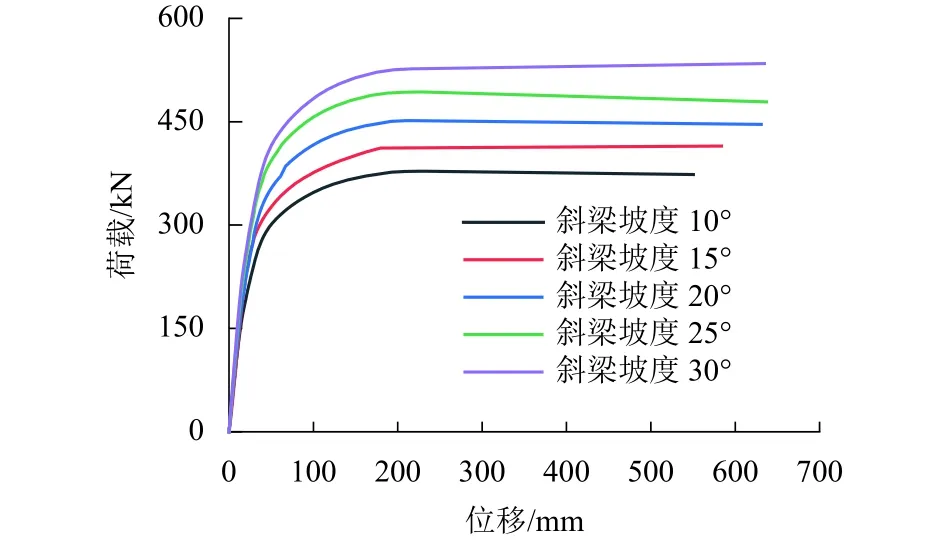
图7 HSR 系列模型荷载-位移曲线Fig.7 Load-displacement curves of HSR series models

2.2 高跨比

高跨比对门式刚架的失稳模态影响较大，限制了稳定承载力的发挥.为了分析高跨比对门式刚架的稳定承载力的影响，在基准模型PF-BASE的基础上，仅改变模型的高跨比，其他参数保持不变.模型的具体参数和有限元分析结果见表5，荷载-位移曲线见图8.

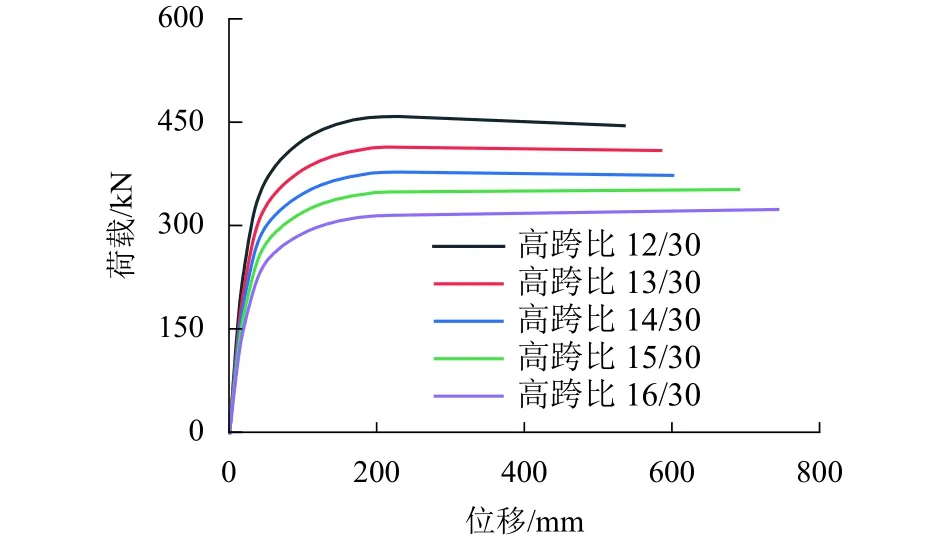
图8 RS 系列模型荷载-位移曲线Fig.8 Load-displacement curves of RS series models

由表5和图8可知：门式刚架的稳定承载力随着高跨比的增加不断降低；相比高跨比为12/30的模型PF-RS-12，高跨比增大至13/30、14/30、15/30、16/30时，门式刚架的稳定承载力分别减小了9.7%、17.6%、23.1%、29.4%.

2.3 陶脑直径

区别于其他刚架，冷弯型钢蒙古包刚架包含陶脑，为研究陶脑对蒙古包刚架稳定承载力的影响，对陶脑直径进行参数分析.在基准模型PF-BASE的基础上，仅改变模型的陶脑直径，其他参数保持不变.模型的具体参数和有限元分析结果见表6，荷载-位移曲线见图9.

表6 不同陶脑直径下模型有限元分析结果Tab.6 Finite element analysis results of models with different toono diameters

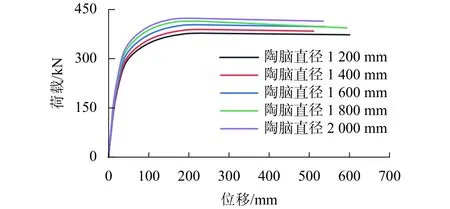
图9 TN 系列模型荷载-位移曲线Fig.9 Load-displacement curves of TN series models

通过有限元计算发现，不同陶脑直径刚架的失稳类型均为对称失稳，由表6和图9可知：不同陶脑直径刚架的失稳类型均为对称失稳；陶脑直径的增加间接增加了斜梁的刚度，门式刚架的稳定承载力随着陶脑直径的增加而增大；相比陶脑直径为1200 mm的基准模型 PF-BASE，陶脑直径增大至 1400、1600、1800、2000 mm，门式刚架的稳定承载力分别增加了 3.0%、6.8%、9.7%、12.0%.有限元模型破坏形态见图10.

图10 部分模型破坏形态Fig.10 Failure modes of partial models

规范[12]的柱长度计算方法适用于柱脚铰接的门式刚架，不符合本文的计算要求.从实际工程计算的角度出发，采用计算长度系数法来计算刚架的稳定承载力，根据规范[13]可查得关于柱的计算长度系数.由表7可知：RS系列和TN系列模型的计算长度系数模拟值和规范值较为接近，差值在0.70%～4.67%，承载力计算结果偏于安全；HSR系列模型的计算长度系数模拟值和规范值差值在0～24.01%，且差值随着斜梁坡度的增大而增大，规范[13]计算刚架承载力过于保守.斜梁坡度的增加使刚架产生了不同程度的拱效应，规范[13]中柱计算长度系数的计算因为忽略了斜梁的轴力，导致计算结果存在较大偏差.

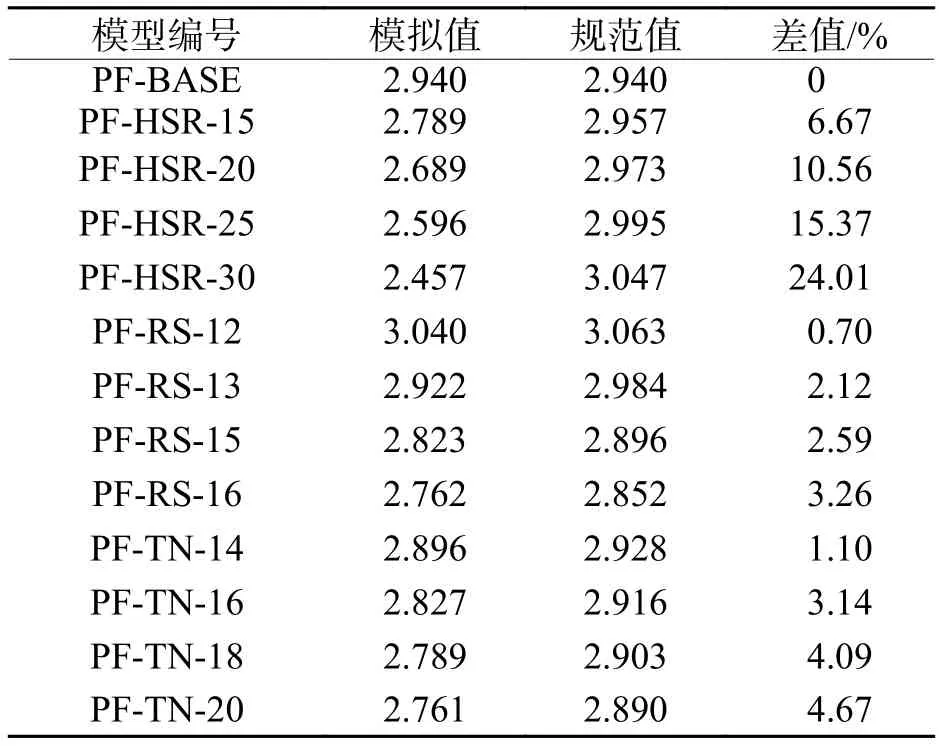
表7 柱计算长度系数模拟值与规范值对比Tab.7 Comparison between simulated values and standard values of column calculated length coefficient

结合试验与有限元分析结果，综合考虑斜梁坡度对刚架稳定承载力和柱顶侧移的影响，本文建议此类型刚架斜梁坡度设计在20° 以内，此时规范[13]对于柱计算长度系数的计算误差在0～10.56%，刚架稳定承载力具有一定安全储备，符合工程设计要求.

4 结 论

本文基于试验和有限元模拟对带陶脑的冷弯型钢蒙古包刚架的平面内稳定性进行研究，所得结论如下：

1）试验和有限元结果表明，带陶脑的冷弯型钢蒙古包刚架在竖向荷载作用下，由于梁的失稳先于柱的失稳，破坏形态以伴随局部屈曲的S形挠曲整体失稳为主，整体刚架并未全部进入塑性状态或仍处于弹塑性状态.

2）进一步的参数分析表明，相比斜梁坡度为10°、高跨比为 12/30 和陶脑直径为 1200 mm 的门式刚架，斜梁坡度从10°～30° 变化时，门式刚架的稳定承载力提升9.7%～41.3%；高跨比从12/30～16/30变化时，门式刚架的稳定承载力下降9.7%～29.4%；陶脑直径从 1400～2000 mm 变化时，门式刚架的稳定承载力提升3.0%～12.0%.

3）通过对试验和有限元结果分析，增大斜梁坡度可有效提高门式刚架的稳定承载力，同时增加斜梁的线刚度、节点和柱脚的刚度，降低高跨比等措施可以提高门式刚架的稳定性能.当门式刚架的跨度较大，可增加斜梁坡度防止发生跃越失稳.

4）综合考虑斜梁坡度对刚架稳定承载力和柱顶侧移的影响，建议斜梁坡度设计在20° 以内，此时规范[13]对于柱计算长度系数的计算误差在0～10.56%，偏于安全，满足工程设计要求.