土中水膜厚度变化规律及未冻水含量预测方法

2022-02-11万旭升颜梦宇路建国晏忠瑞

干旱区研究 2022年1期

万旭升，颜梦宇，路建国，晏忠瑞

（西南石油大学土木工程与测绘学院，四川成都 610500）

我国冻土面积分布广泛，多年冻土和季节性冻土面积之和超过国土面积的70%［1］。寒区工程建设面临因水热相互作用引发的冻胀融沉现象，严重制约着公路、铁路以及构筑物等基础设施建设。水分是土体发生冻融的物质基础，未冻水含量的改变直接影响冻土的热力学及变形特性。同时，未冻水含量随温度变化规律也是水热数值计算的必要条件。

已有试验研究表明冻土中的未冻水主要受土质、外界条件（包括温度和压力）、盐分以及冻融过程等因素的影响［2-5］。水分冻结随着土体颗粒粒径减小、含盐量增加、液体饱和度减小、土颗粒活化比表面积增大而难度增加［1］。随着测试技术的不断发展，核磁共振法、时域反射法和频域反射法等［6-9］广泛运用在未冻水含量测试中，通过信号值与温度的对应关系回归不同温度下的未冻水含量值，建立未冻水含量-温度关系。Anderson 和Tice［10］通过大量室内试验，依据试验数据首次发现未冻水含量随温度降低呈现指数函数减小，并给出了经验公式。随后，此种关系得到了进一步改进及发展［11-12］。Clapeyron 方程建立了冰、水压力与温度之间的联系，被广泛运用到水热模型计算中［13-15］，该方程阐明了水分冻结主要取决于冰水压力的变化。Shoop 和Bigl［16］通过土水特征曲线获取了冻融过程中的水分冻结曲线并预测了未冻水含量随温度变化规律。Zhang 等［17］考虑了土孔隙中冰对水的吸附作用，改进了一般的土体冻结曲线。基于毛细管压力理论，Dall’Amico 等［18］通过将Clapeyron 方程和源于van Genuchten 模型的土-水特征曲线相结合，建立了水分冻结曲线与土水势的关系，随后就有学者证明了此方法的合理性［19］。Sheshukov和Niber［20］结合简化后的Clapeyron 方程，拓展了未冻水含量预测公式，在土水特征曲线中引入了残余含水量。也有学者根据孔隙大小分布函数，基于孔隙水从大孔隙到小孔隙的冻结顺序，建立了理想成冰条件下的土中水冻结模型［21-22］。Hitchcock 等［23］基于均匀成核理论、孔隙堵塞及单一孔隙理论阐释了液体在介孔材料冻融滞后机理。

多孔介质中冰晶预融现象为未冻水含量的求解提供了新的思路。Cash 等［24］基于预融理论建立了负温下等粒径球状颗粒堆积体系的液态水比例组成，并将未冻水含量简化为过冷度的函数。Wettlaufer［25］揭示了冰-液接触面以及冰晶表面内在联系，预融行为明显受介质中杂质的影响。Hendrik和Wettlaufer［26］考虑了多孔介质中杂质浓度以及固体颗粒表面电荷密度的影响，建立了理想等颗粒体系预融理论。然而，由于土中土颗粒粒径范围分布较广泛，预融理论在土中并未得到广泛的应用。本文在已有多孔介质预融理论的基础上，提出针对土体的体积未冻水含量计算方法，并分析了杂质浓度以及颗粒粒径大小对未冻水含量的影响。

1 预融理论

在一个理想等半径球状固体堆积体系中，0 ℃以上纯水充满固体颗粒间隙，假定固体颗粒为均质的、各向同性且表面光滑，且在超低温下孔隙水全部相变为冰晶。发生预融（冰晶开始融化）之前，所有间隙中充满冰晶，当温度上升后，冰晶开始融化，水分的存在形式有薄膜水和间隙水，如图1 所示。薄膜水主要存在土颗粒表面和冰晶接触面，而间隙水主要存在于冰晶与土颗粒所包围的间隙中，其存在温度由冰-液弯曲界面决定。

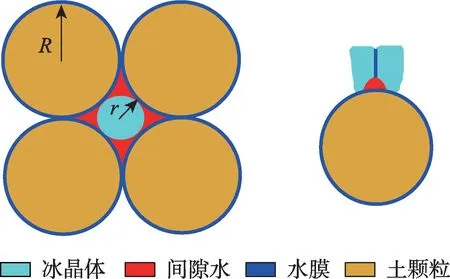
图1 多孔介质中液态水存在形式Fig.1 Existence form of liquid water in porous medium

基于多孔介质预融理论，Cash等［24］首次建立了两种常见堆积，简单立方堆积（Simple Cubic Packing，SC）和立方最密堆积（Face-Centered Cubic Packing，FCC），其颗粒排列方式如图2 所示。堆积体系中液态水的比例与薄膜厚度、颗粒半径以及冰-液接触面半径之间的关系，如公式（1）所示。

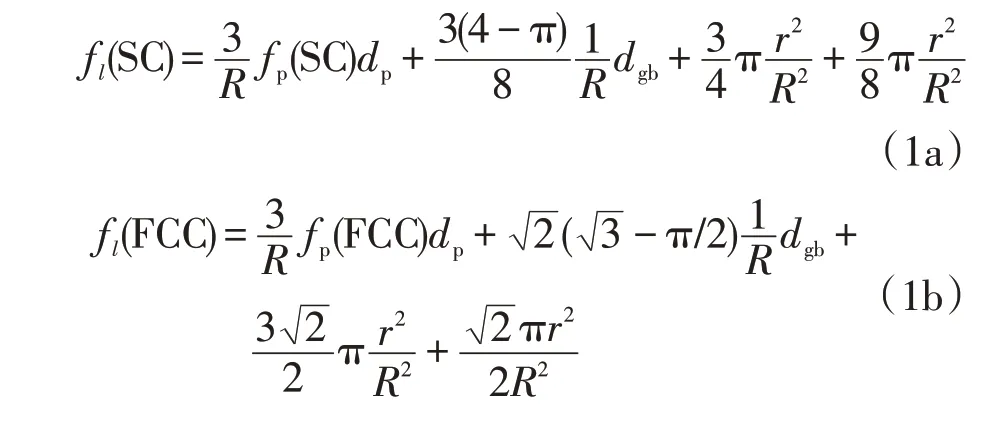
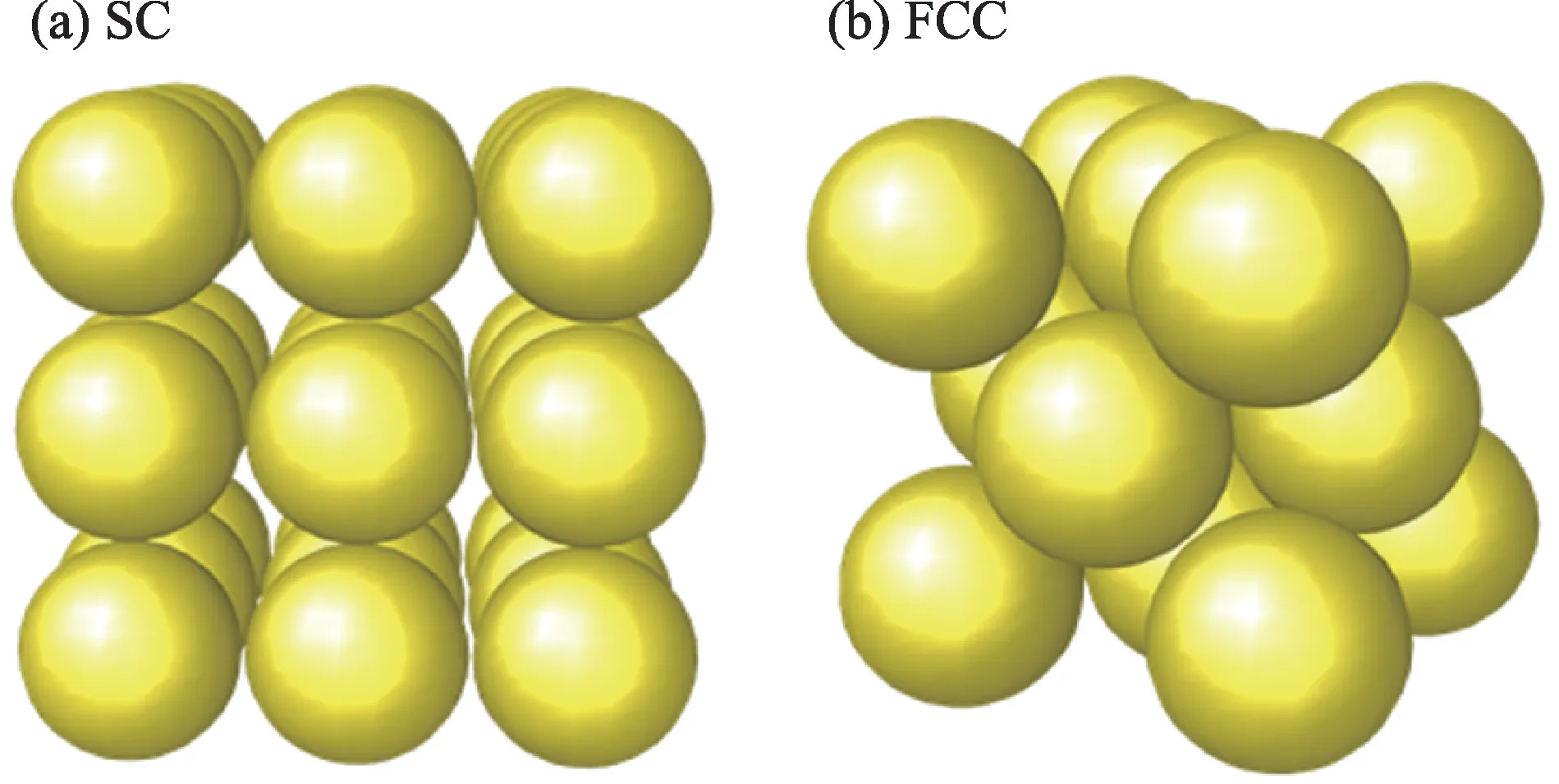
图2 等粒径颗粒排列方式Fig.2 Arrangement of uniform size particle

式中：fp（SC）和fp（FCC）分别表示SC 和FCC 排列下颗粒占总体积的百分比（填充率）；fp（SC）=0.5236［24］；fp（FCC）=0.7405［24］。R表示颗粒半径；dp表示冰颗粒和固体颗粒之间的水膜厚度；dgb表示冰颗粒之间的水膜厚度；fp是球体颗粒占总体积的比例。r表示冰液接触面的半径；其大小会影响冻结温度；可通过Gibbs-Thomson关系确定［27］。

若不考虑系统杂质及表面带电时，固体颗粒表面薄膜厚度d可用公式（2）计算［24,26］。

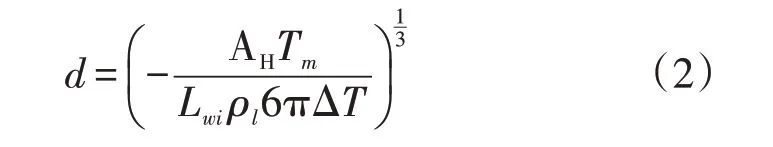
式中：△T表示过冷度，即初始冻结温度降低值（与273.15 K的偏差值）。Lwi表示冰水相变潜热（J·mol-1）。ρl是孔隙溶液摩尔密度（mol·m-3）。Tm是纯水冰点温度，273.15 K。AH是Hamaker 常数［27］，不同物质接触形式会影响Hamaker 常数的取值，故dgb和dp存在一定差异。

对于土而言，系统中含有杂质（盐分），况且很多类型的土颗粒表面带有电荷，故多孔介质体系中应该考虑杂质和颗粒带电量的影响。Hendrik 和Wettlaufer［26］推导了含杂质、带电堆积等粒径颗粒系统中的水膜厚度与过冷度之间的关系，如公式（3）所示：

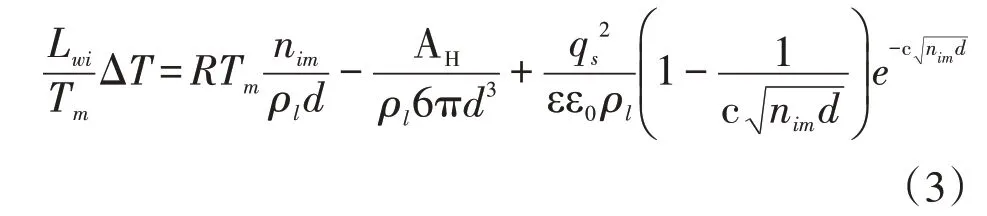
式中：c是常数，可通过公式（4）计算。

式中：nim是土颗粒表面的杂质浓度；ε0是真空介电常数；ε是液态水的相对介电常数；NA是阿伏伽德罗常数；Tm=273.15 K；e是电子电荷；k是玻尔兹曼常数；qs是固定颗粒表面的电荷密度，孔隙溶液摩尔密度ρl在计算中可认为是常数；R是气体常数。公式（3）右边第一项表示杂质浓度影响，第二项表示色散力影响下的界面自由能，第三项表示颗粒表面电荷相关的界面自由能。

以上理论表明等颗粒多孔介质中水分冻结问题得到了较完美的解决，然而对于不同粒径组成的土中水分冻结依然缺乏有效的方法。

2 研究方法

由于土体颗粒分布范围较为广泛，例如粉质黏土通常从几个微米到几个毫米，故现有预融理论在土中应用受到限制。假定土颗粒为球状颗粒，忽略表面粗糙度，视表面为理想光滑球面。基于土体颗粒级配曲线，取足够小的颗粒粒径范围，通常试验测定的也是某一粒径范围Ri土颗粒质量（体积）占总颗粒质量（体积）比例ωi，颗粒分布及粒径划分如图3所示。根据参考文献［28-29］，黄土和砂土的颗粒分布曲线如图4所示。

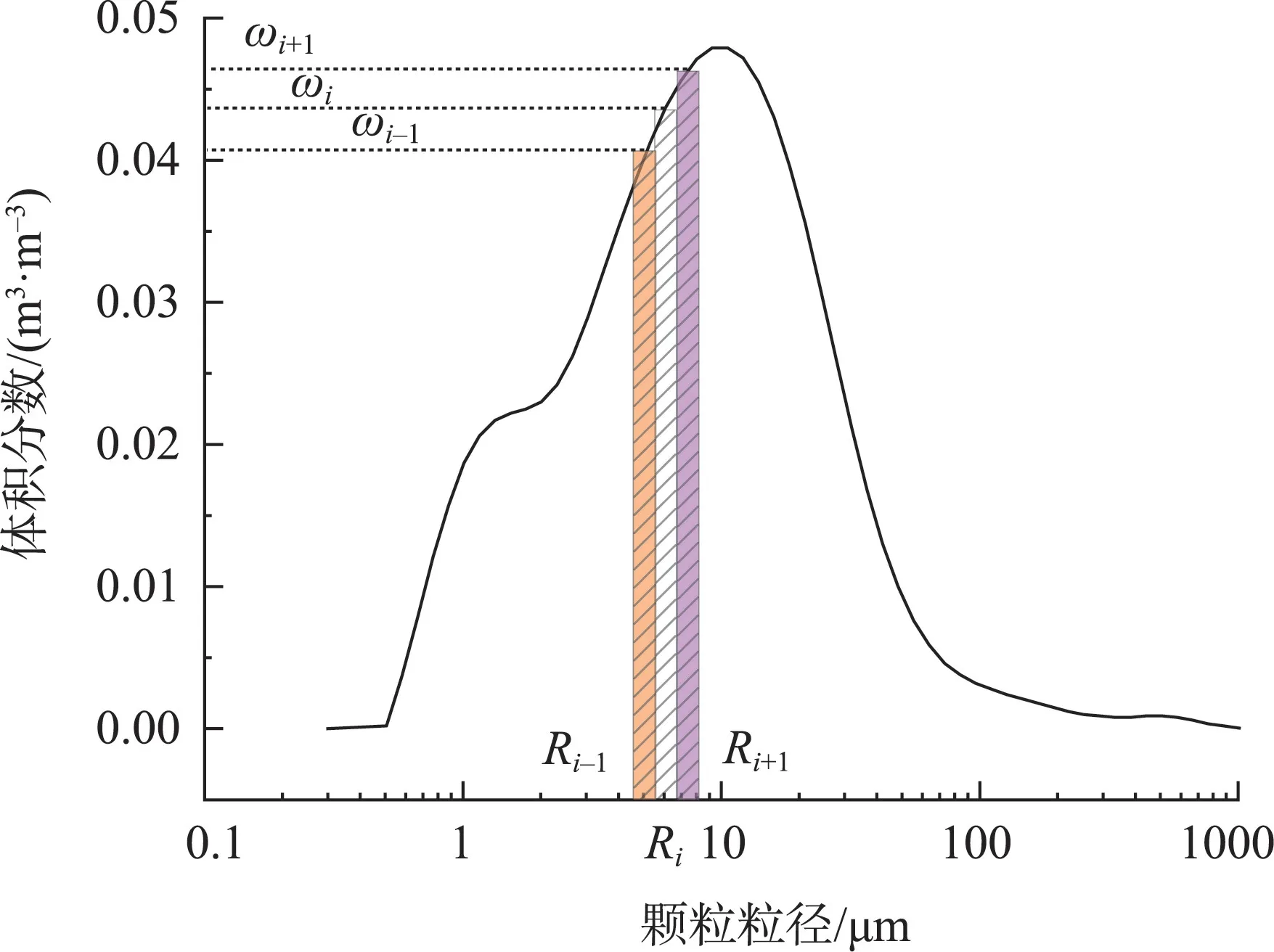
图3 粉质黏土粒径分布Fig.3 Soil particle distribution of silty clay

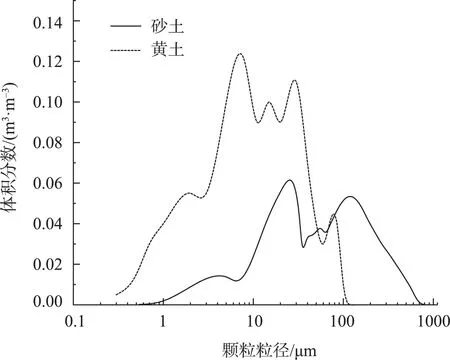
图4 黄土和砂土粒径分布Fig.4 Soil particle distribution of loess and sand

在第i个粒径范围内，认为粒径均匀分布，土颗粒半径均为Ri，若不考虑土的结构性差异，理想认为土体是以上两种颗粒堆积，则可利用联合公式（1）和公式（3）求解该粒径下土中未冻水含量。则总的未冻水含量可用公式（5）求解。

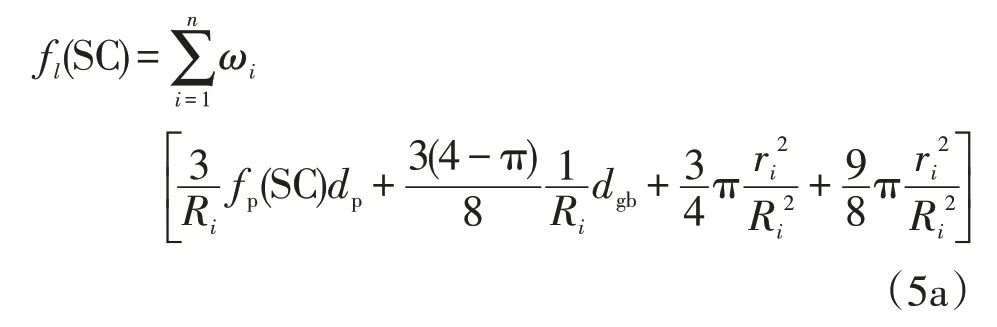
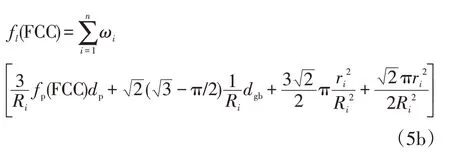
式中：ri表示土颗粒半径为Ri情况下的冰液接触面的半径。然而，公式（5）计算较为繁琐，利用了相同方法重复求解不同粒径下的未冻水含量。针对此问题，本文根据不同粒径土颗粒的体积占比，提出等效粒径的方法，具体计算如公式（6）所示。

式中：Re表示土颗粒等效粒径。

土中土颗粒排列处于SC和FCC之间，为了进一步简化计算，本文采用平均堆积颗粒排列，即取fp（SC）和fp（FCC）的平均值。结合公式（5）和公式（6），土中液态含水量可用公式（7）计算。

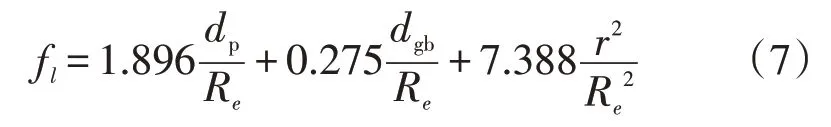
其中冰-液接触面弯曲半径r可通过公式（8）计算［23］。

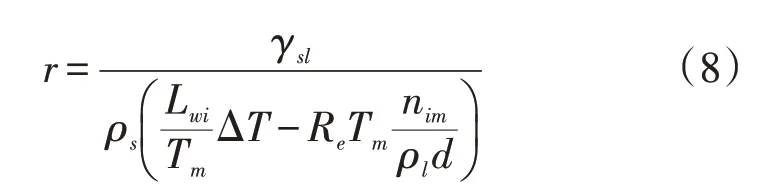
式中：ρs是冰晶的摩尔密度；γsl是冰液表面自由能。对于冰水相变潜热，在温度较小范围内变化时，忽略其变化，取Lwi≈6000 J·mol-1。

随着温度升高无限接近冰点时，假定冰晶处于孔隙中心处，无限小可近似认为一点，如图5 所示，此时冰晶具有最大水膜厚度。则可依据颗粒排列几何关系建立不同土颗粒堆积下的孔隙初始体积浓度与水膜表面杂质浓度之间的关联，如公式（9）所示。

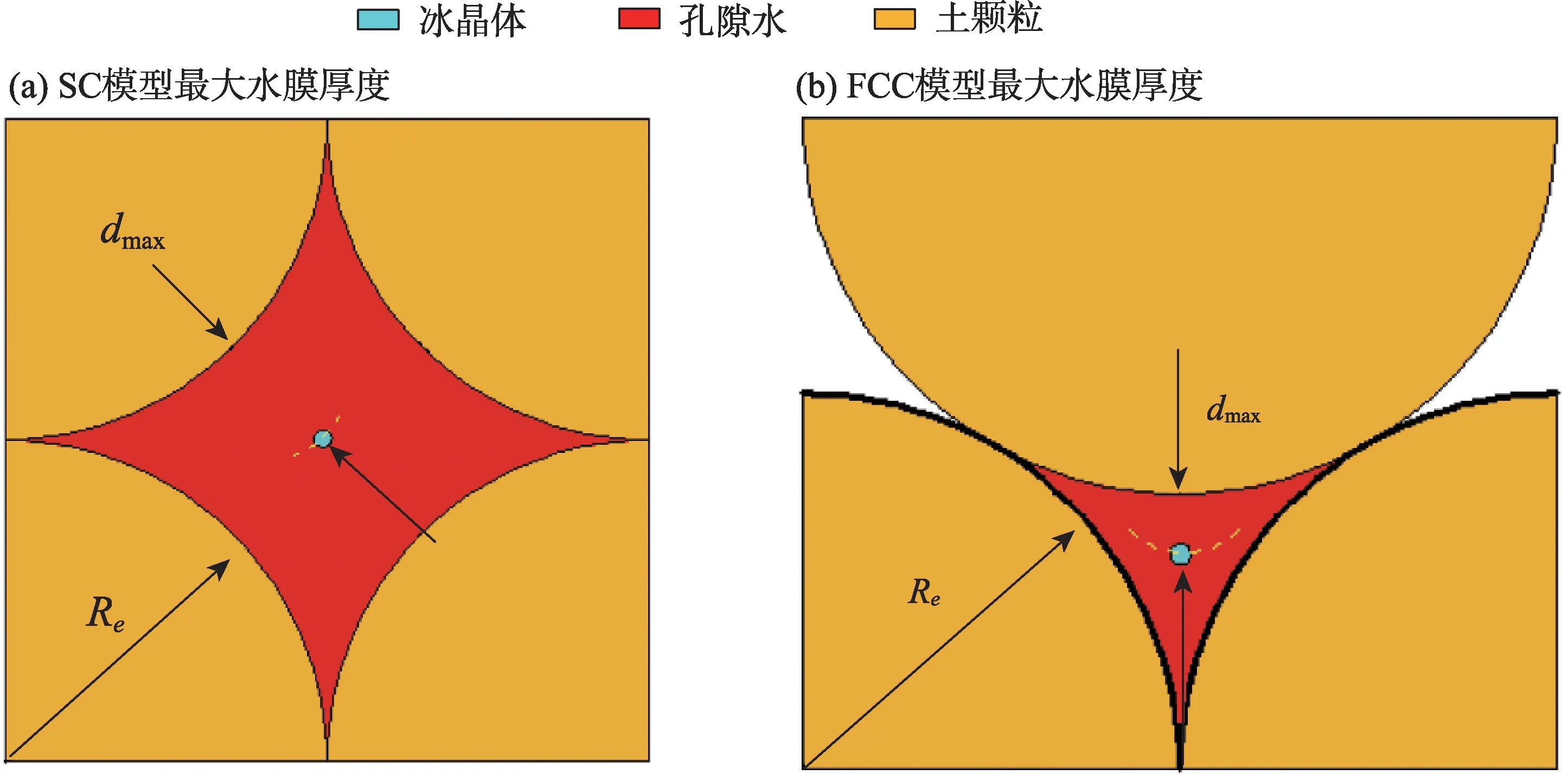
图5 最大水膜厚度示意图Fig.5 Schematic diagram of maximum thickness of water film

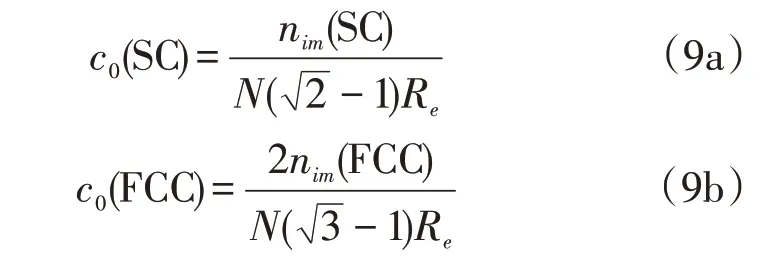
式中：N为单位分子杂质电解离子数，对氯化钠而言，N=2。

为了方便计算土中初始浓度，把孔隙水的初始浓度c0考虑成SC和FCC模型的平均浓度，则杂质浓度可用公式（10）计算：

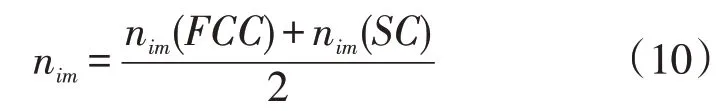
假定初始浓度c0(SC)=c0(FCC)=c0，将公式（9）变形后带入公式（10），可得到土中平均杂质浓度计算公式，见公式（11）。

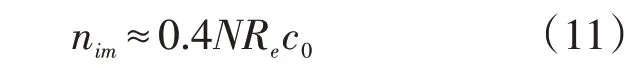
对于固体颗粒，Hamaker 常数通常取9.86×10-19J［24］；对于冰晶接触面而言，表面电荷密度可取0.01 C·m-2以及Hamaker 常数为-3.3×10-22J［26］；R=8.314 J·(mol·K)-1［27］；ε0=8.85419×10-12F·m-1［27］；ε=80.4 F·m-1［27］；e=1.602×10-19C［27］；k=1.308×10-23J·K-1［27］；NA=6.022×1023mol-1［27］；ρl=5.555×104mol·m-3［24］；ρs=5.094×104mol·m-3［24］；γsl=0.03 J·m-2［24］。

3 结果与分析

3.1 土中水膜厚度与未冻水含量变化

一般土颗粒表面带有电荷，以青藏高原粉质黏土为研究对象，取0.1 C·m-2［30］，该类土的初始冻结温度为-0.2 ℃［31］。已有试验研究表明该冰点温度归咎于土中离子浓度［2,32］，基于溶液冰点计算公式［32］可反算出初始离子浓度约0.07 mol·L-1。假定土中盐分类型为典型氯化钠盐，N=2，根据公式（9a）估算nim为4.5×102μmol·m-2。以图3粉质黏土颗粒级配曲线为例，土颗粒等效半径为8 μm。依据公式（3）可建立土颗粒水膜厚度与冻结温度降低之间的关系，计算结果如图6所示。图中斜线表示过冷度随水膜厚度的变化规律曲线，线上点K1、K2表示不同水膜厚度时过冷度值。

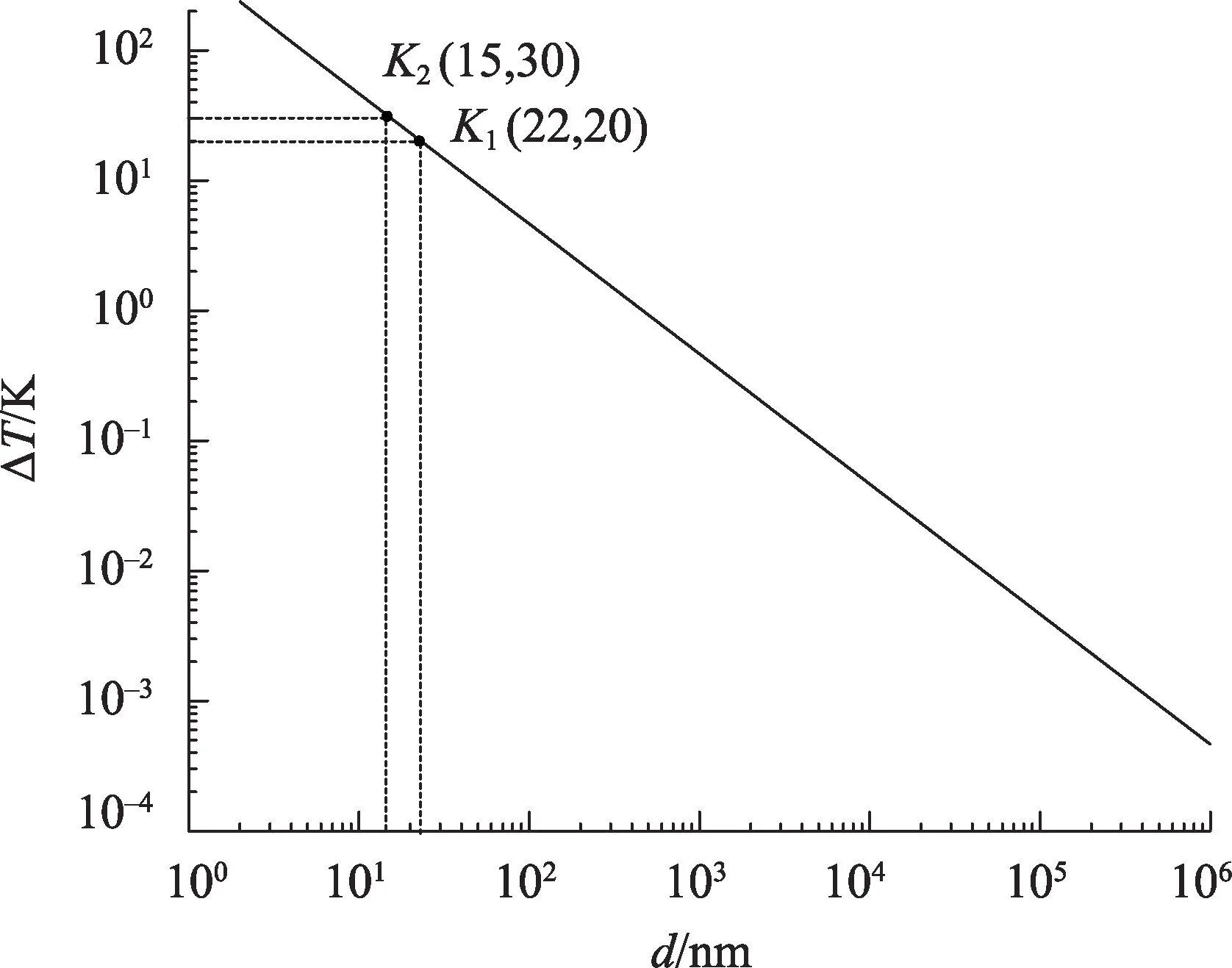
图6 土中过冷度与水膜厚度关系Fig.6 Curve of relationship between degree of supercooling and thickness of water film in soils

从图6 可以看出，土中水膜厚度与温度呈现出线性关系，要使水膜厚度变化小，则要更大的过冷度或者更低的温度。K1和K2两个点表明要使水膜厚度变成22 nm、15 nm，则需要过冷度分别达到20 K 或30 K。若土的初始冻结温度为0 ℃，土体温度从-20 ℃变化至-30 ℃，水膜厚度仅变化7 nm。该规律表明在-30 ℃以下土中水膜厚度变化很小，一般冻土地区土中温度很难使水膜厚度变为几个纳米。故计算土中未冻结含水量，通常考虑-30 ℃以内变化。

类似地，冰晶间的水膜厚度与过冷度可依据公式（3）建立相互关联，弯曲冰-液界面的半径可通过公式（8）求解。将水膜厚度与弯曲液面半径的值代入公式（7）即可求解不同过冷度下的土中未冻水含量，当取等效半径的0.28 倍计算时，计算值与吻合数据较好，计算结果如图7 所示。图中试验数据均来自青藏高原粉质黏土［15,28,31-33］，可以发现试验值与计算值吻合较好，尤其在剧烈冰水相变阶段（-2～0 ℃）。图7表明改进的公式可以求解负温下粉质黏土中未冻水含量。

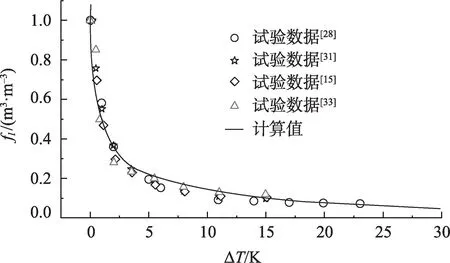
图7 粉质黏土未冻水含量计算值与试验值对比Fig.7 Comparison between the calculated and experimental values of unfrozen water content in silty clay

为了进一步验证模型的适用性，选取不同类型黄土、砂土及黏土试验值进行对比。不同类型土的颗粒表面电荷量差异较小［31］，故在计算中均取0.1 C·m-2。通过公式（6）可计算出黄土和砂土的等效粒径分别为10 μm和56 μm。黏土的等效粒径大约为4 μm［2,34］。

不考虑土中水过冷度，表面杂质浓度与之前粉质黏土一样，同样对等效半径进行缩小，黏土、黄土、砂土分别以等效半径的0.24、0.3、0.36 倍计算，未冻水试验数据均来源于参考文献［18,28,34-35］，计算结果如图8所示。从图8a可以看出，计算值能较好反映未冻水变化规律，当温度较低时，即ΔT＞10 K，预测值比试验值较高。对于砂土而言，计算值与试验值吻合较好，未冻水体积含量迅速减小并趋于稳定，当ΔT＞5 K时，未冻水比例基本不变。而对于黏土，虽然计算值反映了变化趋势，但误差较大，尤其在开始冻结温度段，其主要原因是黏土颗粒的形状呈片状，与假定的球形差距较大。

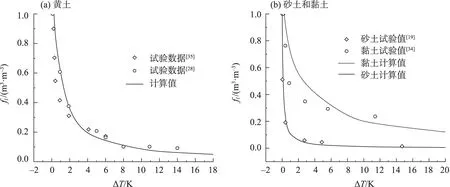
图8 不同土类型计算值与试验值对比Fig.8 Comparison between the calculated and experimental values of different soils

3.2 水膜厚度影响因素

不同物理化学界面能对水膜厚度的影响如图9所示。色散力其与Hamaker 常数相关，对水膜的影响与杂质浓度没有关系，随着水膜厚度减小，过冷度呈线性增大，当水膜减小至几个纳米级时，其逐渐发挥作用。杂质浓度对水膜厚度的变化影响很大，随着浓度增加，相同过冷度下水膜厚度减小越来越困难，说明水分冻结难度增大。土颗粒表面电荷密度对水膜厚度的影响极易受杂质浓度的影响，随着浓度增大，土颗粒表面电荷对水膜的影响越来越小；相反，当杂质浓度减小至0.01 μmol·m-2，土颗粒表面电荷密度对土孔隙中水膜变化的作用大于杂质浓度本身的影响。当杂质浓度大于1 μmol·m-2，表面电荷密度对水膜的影响非常小，在计算中可以不考虑。此外，依据公式（3），当颗粒表面电荷密度减弱时，其对水膜的影响也随之减小。

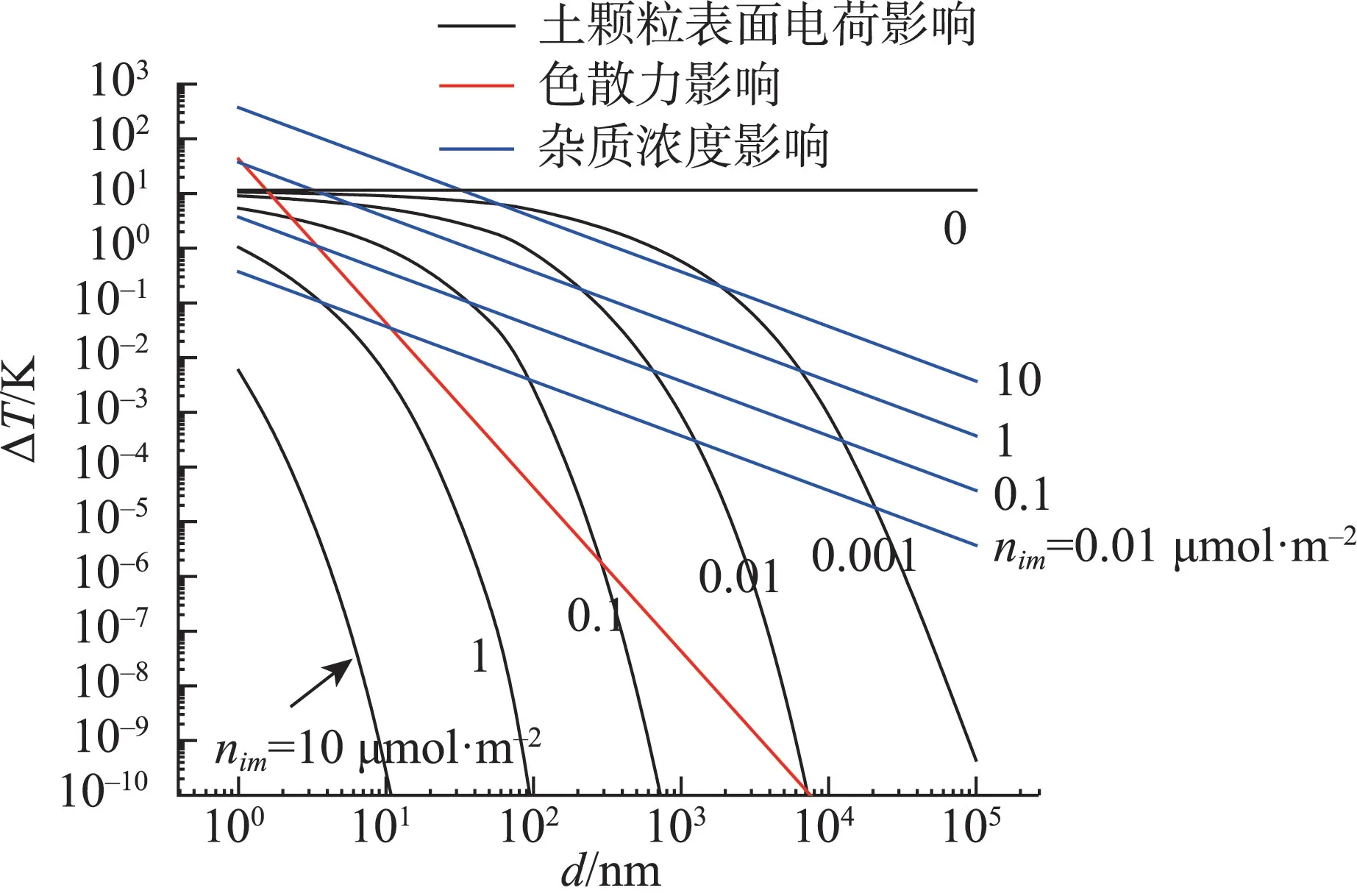
图9 不同杂质浓度及物理化学界面能对水膜厚度影响Fig.9 Effect of different impurity concentration and physical chemical interface energy

3.3 薄膜水和间隙水变化规律及影响因素

对于粉质黏土，颗粒表面水膜，冰晶间水膜以及间隙水所引起未冻水含量的变化如图10 所示。可以看出，土中水分冻结主要由土颗粒表面水膜厚度变化来决定。冰晶间水膜的影响相比土颗粒表面水膜而言较小，两者计算值之间差了一个数量级。而土中间隙水对未冻水含量的影响最小，通过公式（8）得出，较高的初始浓度会减小冰-液弯曲界面的半径，导致r/Re的平方减小很多，致使液态含水量很小。

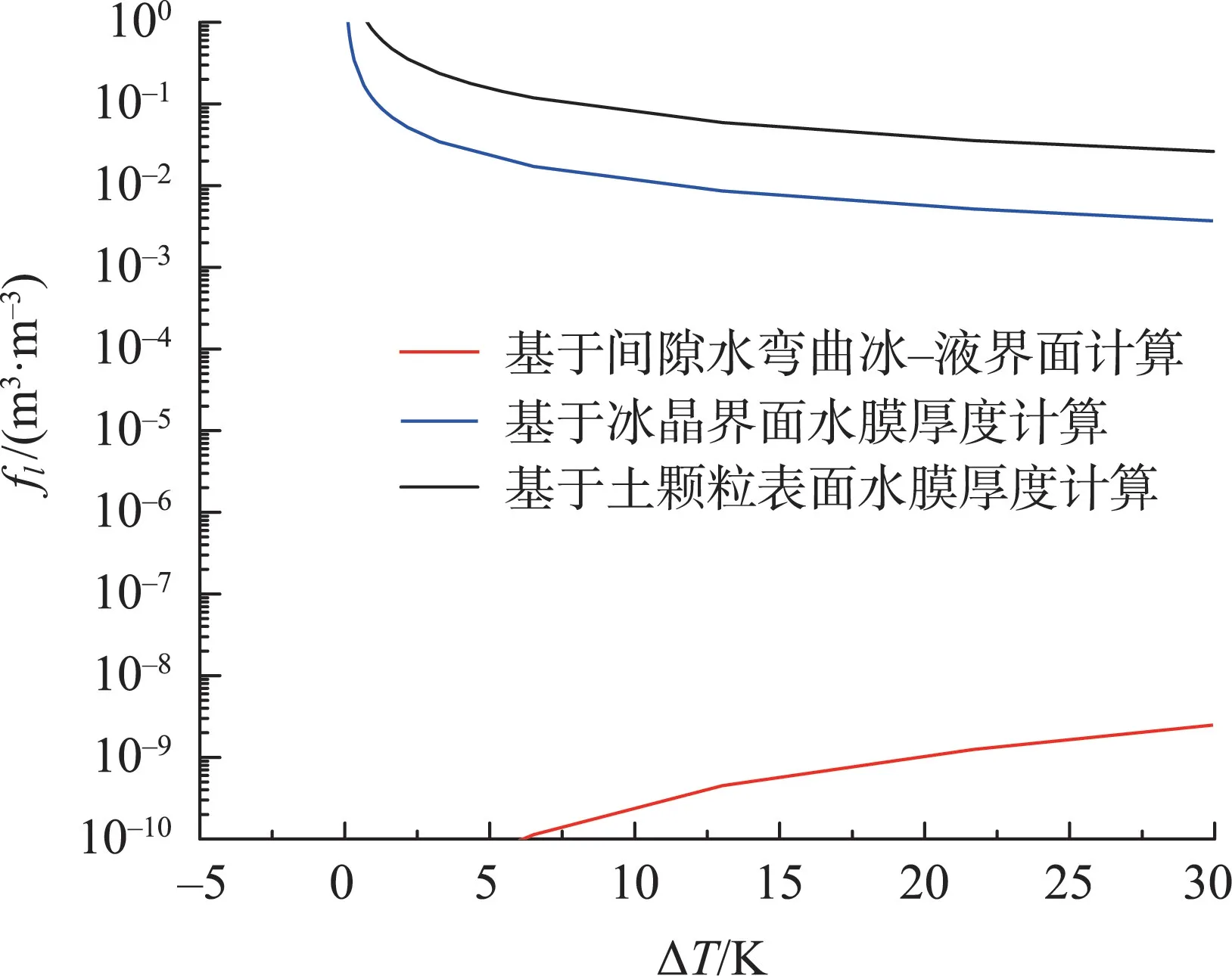
图10 水膜及间隙水对未冻水含量计算值的贡献Fig.10 Construction of water film and interstitial water to calculation of unfrozen water content

当土中杂质浓度变化或土颗粒粒径变化，诸如黏土比粉质黏土的颗粒要细，在此假定不同浓度及粒径条件，未冻水含量计算结果如图11所示。可以发现在浓度较高的条件下（图11a），随着土的等效颗粒粒径减小，未冻水含量增大，表明水在细颗粒土中更难冻结。在浓度较低情况下（图11b），未冻水含量变化表现出相似的规律，但基于间隙水计算得到的未冻水含量所发挥的作用随着颗粒减小愈发明显，在很大温度范围内，超过了基于冰晶间水膜厚度计算的未冻结含水量值。此外，计算结果表明土颗粒等效粒径越细，初始冻结温度较低，低浓度细颗粒的冰-液弯曲界面在水分初始冻结中占主导地位。

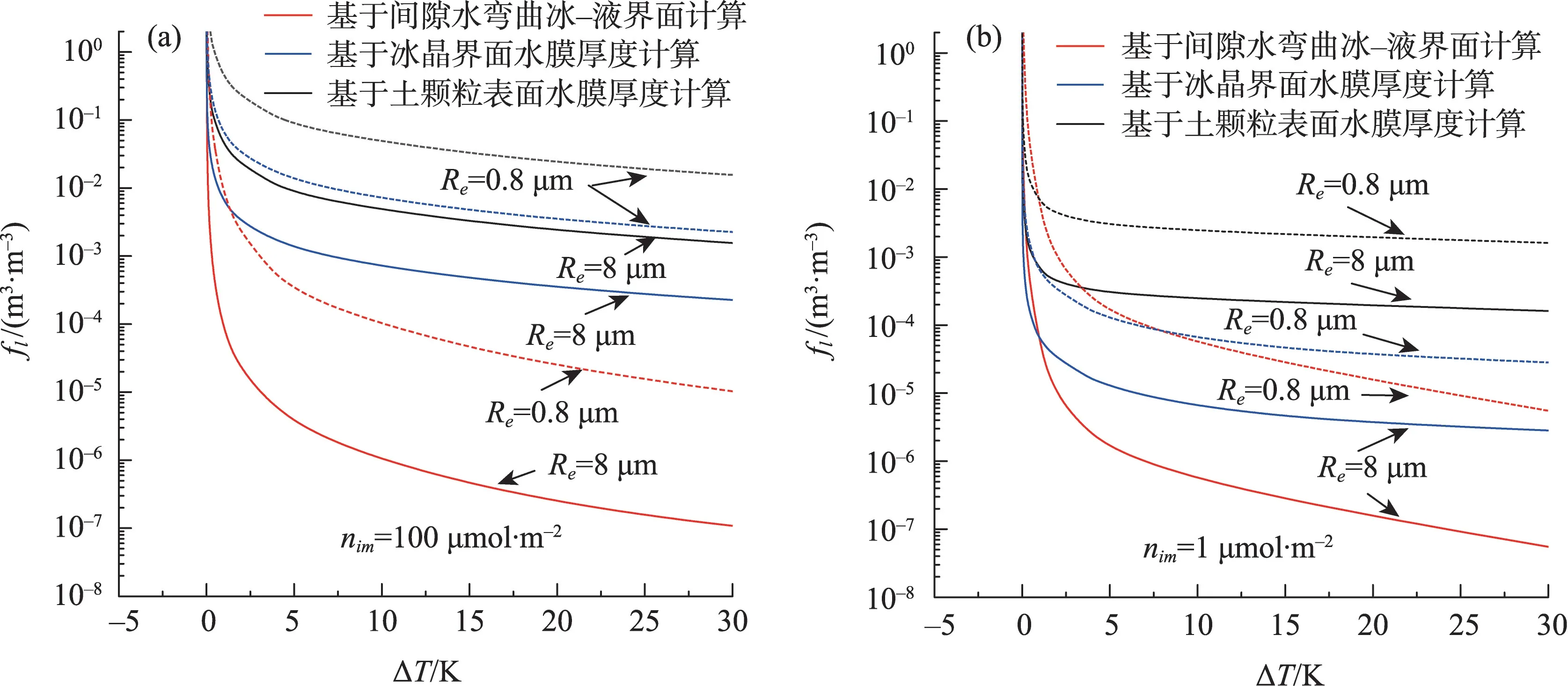
图11 浓度及颗粒半径对未冻水含量的影响Fig.11 Effect of concentration and particle radius on unfrozen water content

4 讨论

经典的指数或幂函数关系［8］在水分剧烈相变阶段（初始冻结温度附近）存在很大的误差，因为指数函数在冰点0 ℃不收敛，且模型中参数随不同初始含水量变化较大。结合土水特征曲线和冻结特征曲线的预测模型［17］很大程度上依赖于初始含水量和残余含水量，且模型中涉及的参数较多。这些未冻水含量模型中的参数没有明确的物理意义，而本文改进的模型物理参数明确，且考虑了土体颗粒大小、杂质浓度、颗粒表面带电特性，并涉及了水分冻结的物理化学微观机理。

Dash 等［27］通过预融理论计算了等粒径聚苯乙烯粉末及石墨化炭黑粉中未冻水含量的分布，发现当半径分别缩小0.15和0.4时计算效果与试验值吻合较好。土颗粒实际排列非常复杂，且颗粒形状并非全是球状体，且土颗粒表面呈现出一定粗糙度。本文在计算过程中采用了等效粒径，当粉质黏土、黄土、砂土分别以等效半径的0.28、0.3、0.36倍计算时，计算值与试验值吻合较好。而对于细颗粒土黏土，计算值与试验值差别较大。此外，在模型中未考虑细颗粒土中特殊结构，大部分黏土中存在如蜂窝结构、絮状结构等特殊形式，与自然排列下的土颗粒分布有一定差距，会影响模型计算精度。同时，计算中缩小半径的处理方式还未有详细阐述。所以颗粒形状、颗粒表面粗糙度、土颗粒的实际排列和土的结构类型等会作为水分微观冻结方面后期研究内容，进而开展进一步研究。