基于多入渗模型的荒漠砂质土壤积水入渗模拟对比

周 宏

（1.西北师范大学旅游学院，西北师范大学河西走廊研究院，甘肃 兰州 730070；2.中国科学院西北生态环境资源研究院，中国生态系统研究网络临泽内陆河流域研究站，甘肃 兰州 730000）

入渗是指水分进入土壤的过程，而土壤水分入渗作为水文循环中关键环节，对连接地表水资源和降雨以及调控水分分配至关重要［1-2］，许多学者基于不同尺度、不同土壤和气候区域进行了深入研究［3］。在非均质土壤中提出了用以表征入渗速率、累积入渗量等参数入渗模型，包括Kostiakov 和Horton经验模型，Philip近似物理模型和Green-Ampt、基于Richard 方程算法的Hydrus-1D/2D/3D 等物理模型。但不同土壤条件中模型应用范围存在差异，Kostiakov方程简单，能够很好地拟合实测入渗数据，但其参数无物理意义，无法解析入渗过程详细信息［4-5］，Philip是估算最终入渗速率较常用的模型，已在砂质土壤［6］、黏土-壤土农田中得到了验证［7-8］。Green-Ampt模型主要用于均匀土壤介质中的积水入渗，借助其简便性和物理基础，扩展模拟了一系列条件下的入渗、降雨和径流过程［9-12］。非饱和水分运移过程模拟主要采用基于质量守恒定律和达西定律的Richards 方程来表达［13］，但Richards 方程通常用非线性描述，无法求解析解，导致计算过程较复杂，特别在复杂的初始和边界条件中。由美国农业部盐渍土实验室开发的Hydrus-1D 软件可广泛用于模拟饱和-非饱和介质中一维土壤水分运移，其Hydrus-2D/3D 软件应用于模拟二维或三维土壤水分运移和空间分布，并已获得大量的验证和应用［14-16］。

干旱区绿洲荒漠区有许多代表性的景观单元类型，如荒漠、沙丘和农田等［17］。其中沙丘及其丘间低地在荒漠生态系统水力连接和水循环中扮演着重要的角色［18］，事关荒漠生态系统的结构功能演化和绿洲稳定。在年均降水量小于200 mm干旱区，降水具有降水稀少、变率大、历时短等特征［19］，尽管降水量少，但确是干旱生态系统中唯一水分补给来源，尤其是储存在浅层土壤水分调控地表径流和降雨入渗及其再分配过程［20］。水分入渗作为土壤水文过程重要组成部分，许多学者已针对不同尺度的干旱荒漠生态系统土壤包气带水分入渗方面开展了广泛研究［21］。积水入渗是由于入渗强度小于降雨强度导致一种压力入渗［22］，尤其在土壤结皮较厚的干旱区，水分停留时间延长，相应入渗量会降低，易导致积水入渗现象发生，而在丘间低地入渗速率降低，会导致下垫面土壤含水率提高［23］。

国内外有关土壤入渗过程研究方法较多，如土柱回填法、单双环入渗、Hood土壤入渗仪等，其中采用单环定水头对水分入渗进行原位测量，可用于估算土壤水分入渗特性［2,24-25］。然而，由于野外试验需要花费大量的时间和费用，而简单、可靠的渗透试验数据处理方法显得尤为必要。但由于土壤异质性，导致大量入渗模型在模拟土壤水分变化时仍然有很大局限性。因此，不同时空条件下，土壤水分运移过程模型的识别和选择仍需不断尝试，基于此，本研究通过野外原位入渗试验，分析砂质土壤中水流入渗过程并评价不同模型在土壤水分入渗模拟中的性能，旨在寻找降雨条件下适宜模型，以便合理预测沙丘积水入渗过程，提升对荒漠沙丘局地土壤包气带水分运移及交换过程认知。

1 材料与方法

1.1 研究区概况

研究在巴丹吉林沙漠北部边缘的中国科学院临泽内陆河流域研究站进行，该站属于中国生态系统研究网络（CERN），地理位置位于100°9′30″E，39°24′41″N，海拔1381 m。年均气温7.5 ℃，最高气温39 ℃，最低气温-27 ℃，年均潜在蒸发量变化为1900～2088 mm，全年湿度变化为7.3%～80.9%。多年平均降雨量为120 mm，高峰出现在7—9 月。降雨是研究区域最敏感的气象因子，2006—2017年该区域共接收到降雨事件约500次（图1），地下水埋深约为4.9 m，地下水的饱和毛管上升不会影响表层土壤水分。

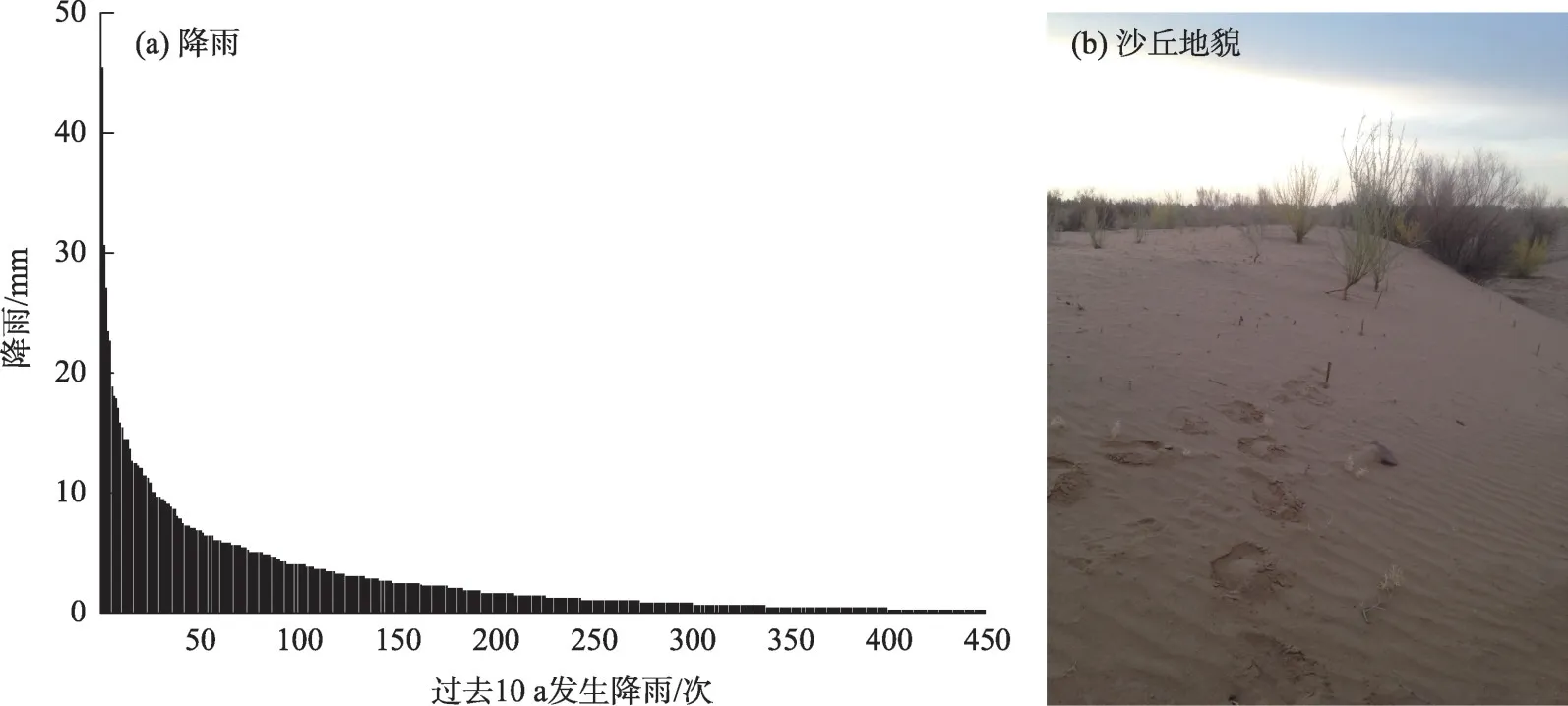
图1 试验区多年降雨状况和干旱区沙丘-丘间低地地貌Fig.1 Location of experimental site,rainfall and image of a mature dune slack in arid region

1.2 原位试验与设计

在选定的试验区开展单环入渗试验，首先去除土壤表面可能阻碍入渗环插入的残留物，然后用落锤将铁环夯实，嵌入深度约为5 cm（铁环尺寸：直径20 cm，高度为30 cm）。此外，要注意保持铁环边缘与土壤表面垂直，并尽量减少对土壤扰动，试验开始前在环内垫上滤纸，以防止水流破坏土壤表面，造成水头不均匀（图2），并沿着入渗环下端中心位置插入土壤水分观测探头，探头插入土壤剖面深度依次为10 cm、20 cm、40 cm、60 cm、80 cm，数据采集器连续收集土壤水分变化值，时间间隔1 min（图2）。

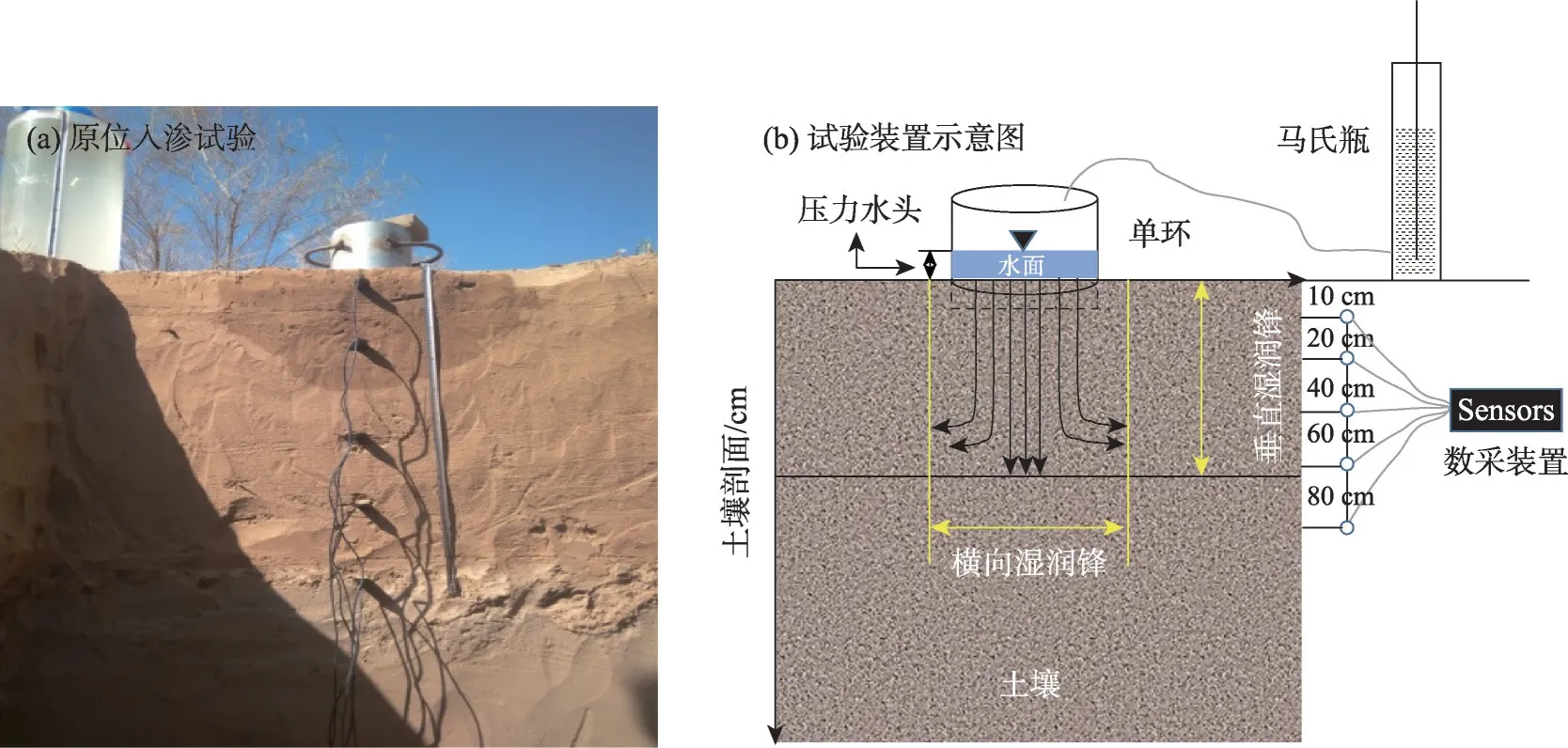
图2 单环试验示意图及土壤包气带剖面和探头深度Fig.2 The profiles of soil vadose zone and schematic diagram of single ring experiment

1.3 土壤样品收集与分析

在研究区0～80 cm内用土钻分层采集原状土壤样品，土样均来自入渗剖面中心，然后烘干法求土壤容重，浸泡法测饱和含水量，激光粒度仪获取土壤粒径组成，定水头法求饱和导水率KS，土壤水力参数是水分运移模拟的关键因素，主要特征数据见表1。

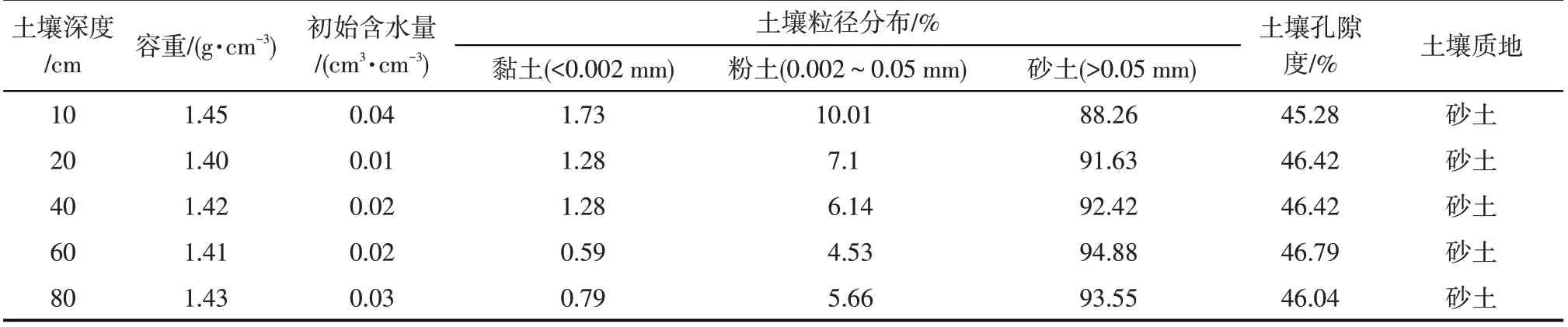
表1 试验场地土壤水力学和物理特性Tab.1 Soil hydraulic and structural properties in experimental site

2 模型描述

2.1 Hydrus-1D/3D模型理论

三维水流运动可以用如下Richards方程来描述:

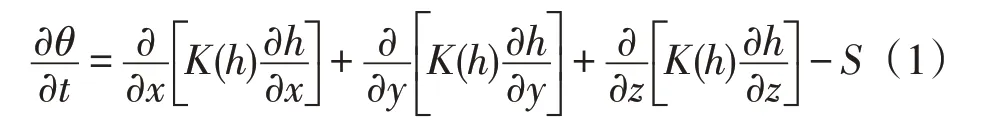
式中：θ为体积含水率（cm3·cm-3）；h为压力水头（cm）；t为时间（h）；K（h）为非饱和导水率函数（cm·d-1）；z为向上正的空间坐标（m）；S为汇源项，通常表示根吸水率（S-1），本试验在裸露沙丘进行，不考虑根系吸水。其中简化的一维水流运动方程如下：

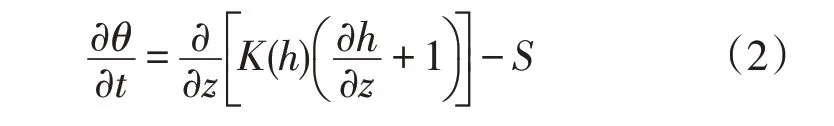
2.1.1 土壤水力性质 用Van Genuchten-Mualem（VG）模型描述土壤水分特征曲线，其土壤水力函数如下：

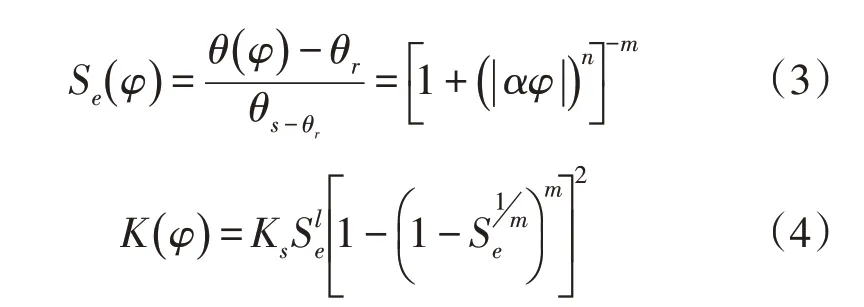
式中：θr和θs分别为土壤残余含水量和土壤饱和含水量（cm3·cm-3）；Se为饱和度（无量纲）；Ks为饱和导水率（cm·d-1）；n为孔径分布指数（无量纲）；m=1-1/n为土壤水分特征曲线参数；φ为土壤基质势；l为孔隙连通性参数（无量纲）。基于VG模型土壤水力参数见表2。

表2 试验地不同剖面土壤水力参数组成Tab.2 Soil parameters for different soil layers in the experiment site

2.1.2 初始和边界条件

（1）基于Hydrus-2D二维计算模拟

模拟区域入渗面以上DA、BC为不透水边界；地表DE、FC为大气边界，下底面AB为自由排水边界；EF 在入渗开始后很快达到饱和，为定水头边界，其边界和初始条件如下：

①初始条件：

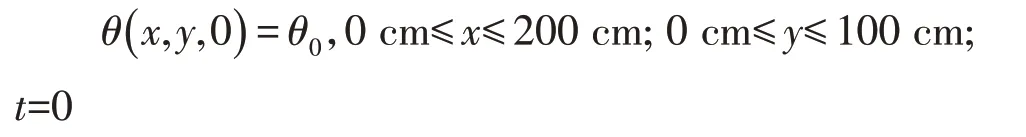
式中：θ0为初始含水量（cm3·cm-3）。

②边界条件：

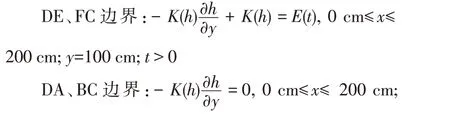
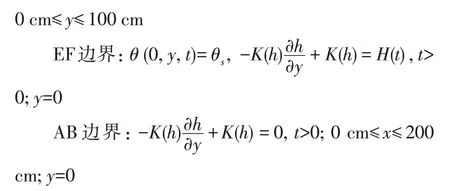
式中：E(t)为入渗速率；H(t)为恒定水头。

（2）基于Hydrus-3D三维计算模拟

三维模拟区域入渗面OPNM 为大气边界；侧面OPGH、GPMJ、MNIJ 和HION 为不透水边界，下底面GHIJ为自由排水边界；以直径R=20 cm入渗圆面开始后很快达到饱和，为定水头边界，其边界和初始条件如下：

①初始条件：

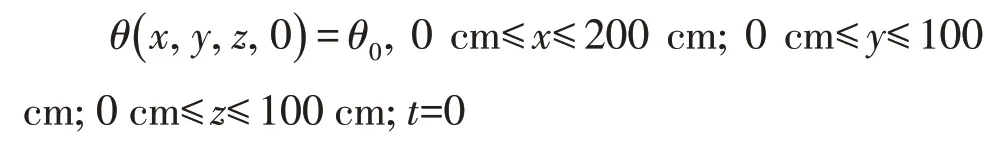
②边界条件：

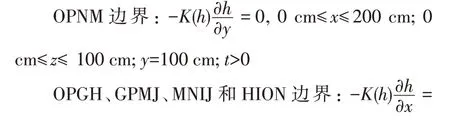
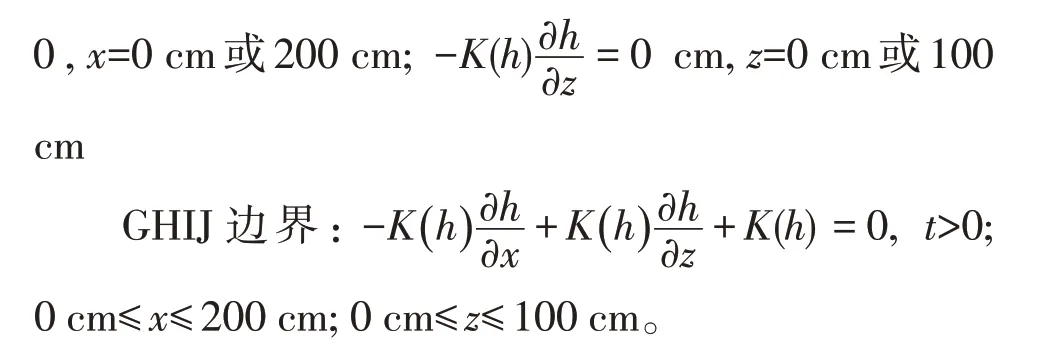
二维与三维模拟均采用1 cm 压力水头作为单环入渗下的水流边界条件（图3），并将模拟区域离散成径向网格间距为2 cm、垂直网格间距为1 cm的有限元，总模拟时长12 h。

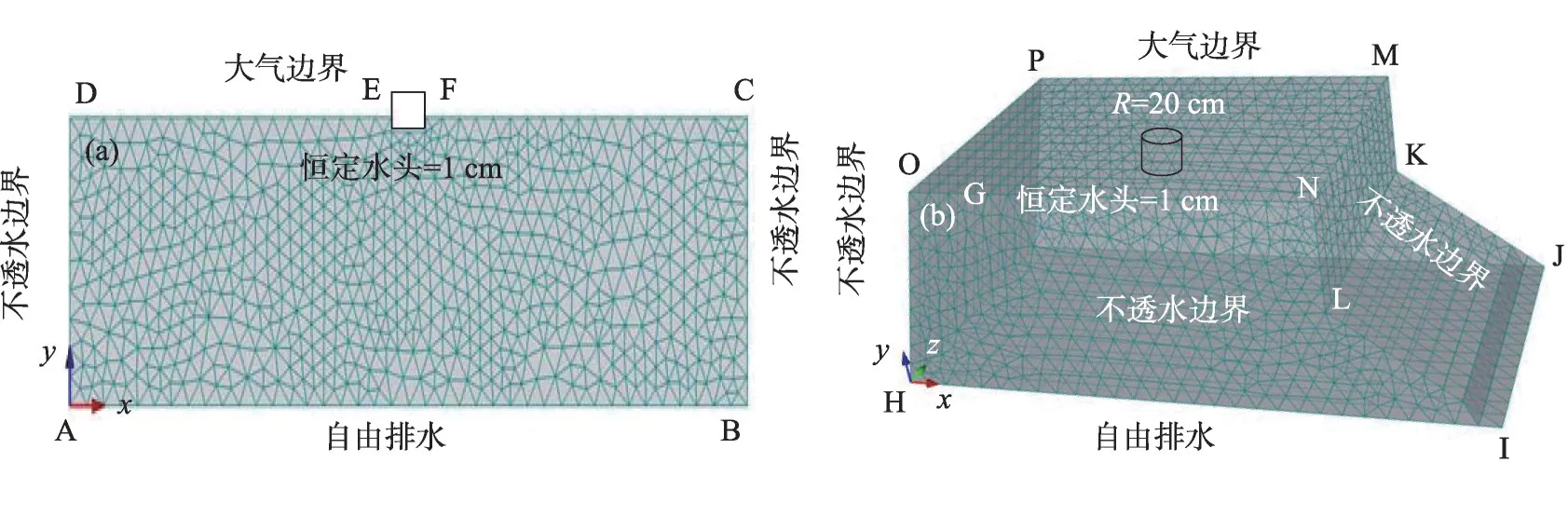
图3 Hydrus-2D/3D模拟区域及边界条件Fig.3 The Hydrus-2D/3D simulation domain and boundary conditions

2.2 入渗模型理论

2.2.1 Green-Ampt Green-Ampt 模型最初是利用达西定律对定水头条件下土柱积水入渗进行分析，入渗方程如下：

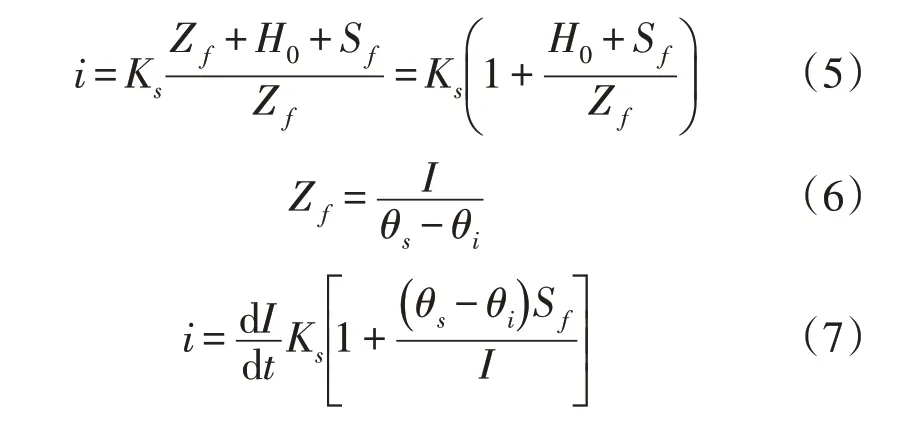
式中：I为累积入渗量（cm）；i为入渗率（cm·min-1）；Ks为饱和导水率；Sf为湿润锋面吸力；Zf为概化的湿润锋深度（cm）；θi为初始土壤含水量（cm3·cm-3）。

分层均质土壤入渗时，通过整合Green-Ampt模型推导出累积入渗量和湿润锋随时间变化的隐函数，分别表示如下：

式中：D为土层厚度（cm）；下标i、s、j、N分别表示初始状态、饱和状态、土层数和饱和层数。

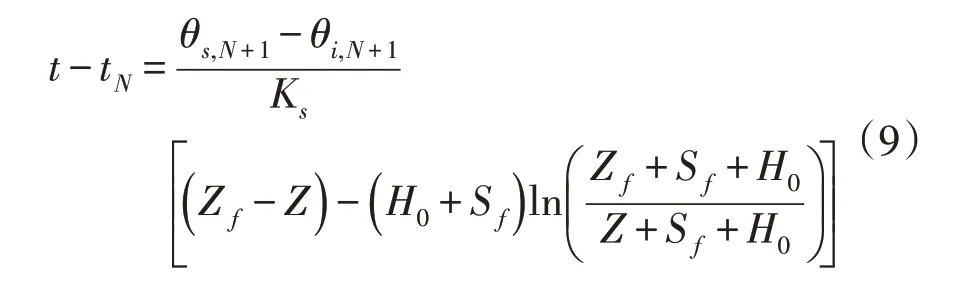
式中：tN为湿润锋到达第N层界面所需时间（min）。

2.2.2 Philip Philip模型最初由Philip提出，累积入渗量和入渗率表示为：

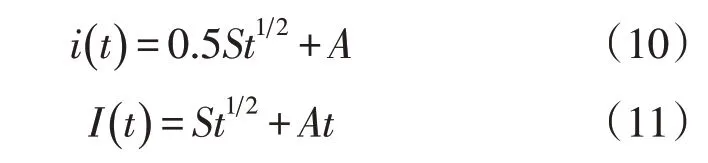
式中：A是关于土壤性质和水分导水系数函数（cm·min-1）；S为吸水率，是土壤基质势函数（cm·min-0.5）。

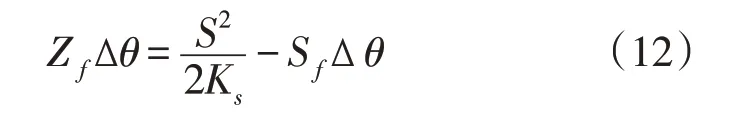
式中：Δθ为饱和含水量和初始含水量的差值。

2.2.3 Kostiakov-Lewis 修正后长周期的Kostiakov 模型描述为［26］：

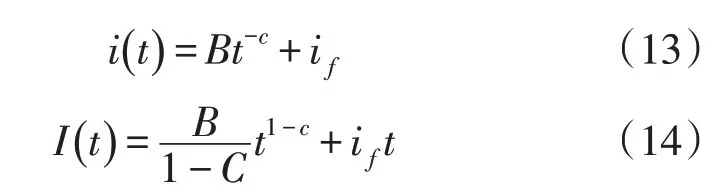
式中：B、C分别为方程参数（C＞0,0＜B＜1）；i（t）、if分别为入渗率和稳定入渗率。

2.3 模拟效果评价

模拟值与观测值比较用以评价模型性能，本研究以决定系数（R2）和均方根误差（RMSE）作为最终评价指标。

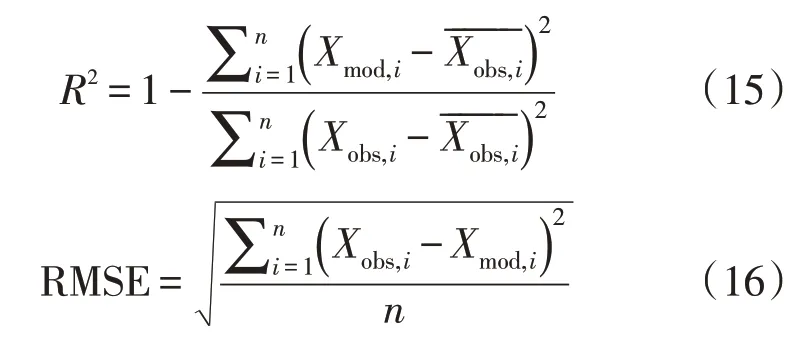
式中：Xobs,i为观测值；Xmod,i为模拟值；为观测样本均值，obs,i代表第i（1,2,…,n）个观测值；n为观测数据总个数。RMSE 指标值越小，表明模拟误差越小，而R2的指标值越接近1，表明模拟精度越高，拟合度越好。

3 结果与分析

3.1 实测数据

结果表明，试验开始后入渗速率持续下降，300 min 左右达到稳定入渗速率0.57 cm·min-1（图4a），累积入渗量随时间增加而递增，观测时段内累积入渗量达到398 cm（图4b），入渗开始后湿润锋同时沿竖直和水平两个方向快速推进，200 min后推进速度趋缓，入渗结束后，水平方向湿润锋距离较垂直方向湿润锋距离增加了45%（图4c）。可以发现幂函数可以较好的拟合实测数据（R2=0.85）。然而，幂函数只是估算土壤水分入渗的一个简单的经验模型，无具体物理参数意义。此外，结果表明，在10～80 cm深度内土壤各个剖面含水量差异明显（图4d），达到稳态土壤含水量随土层深度增加而降低，但20 cm剖面的最大含水率明显低于其他剖面，且均低于饱和含水量，这可能与容重、粒径构成等土壤性质差异有关。

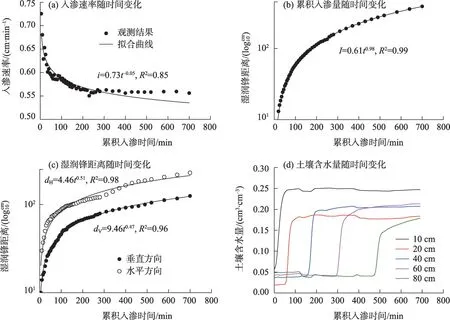
图4 观测时段的入渗速率、累积入渗量、湿润锋距离和土壤含水量变化Fig.4 Dynamic of observed infiltration rate,cumulative infiltration,depth of wetting front and soil water content during the study period

3.2 观测与模拟结果比较

3.2.1 入渗速率 4 种水文模型的入渗率模拟值与观测值对比如图5 所示。结果表明，入渗率的R2系数均值在0.75～0.95，Philip 的R2系数最高（0.95），Kostiakov 的模拟结果略大于观测值，相反Green-Ampt 的模拟结果略低于观测值，尤其在入渗后期。Hydrus-1D 模拟结果与实测匹配较低，决定系数R2较小（0.79）。总之，荒漠砂质土壤积水入渗条件下，Philip 较其他入渗模型能更好地描述土壤水分入渗过程。

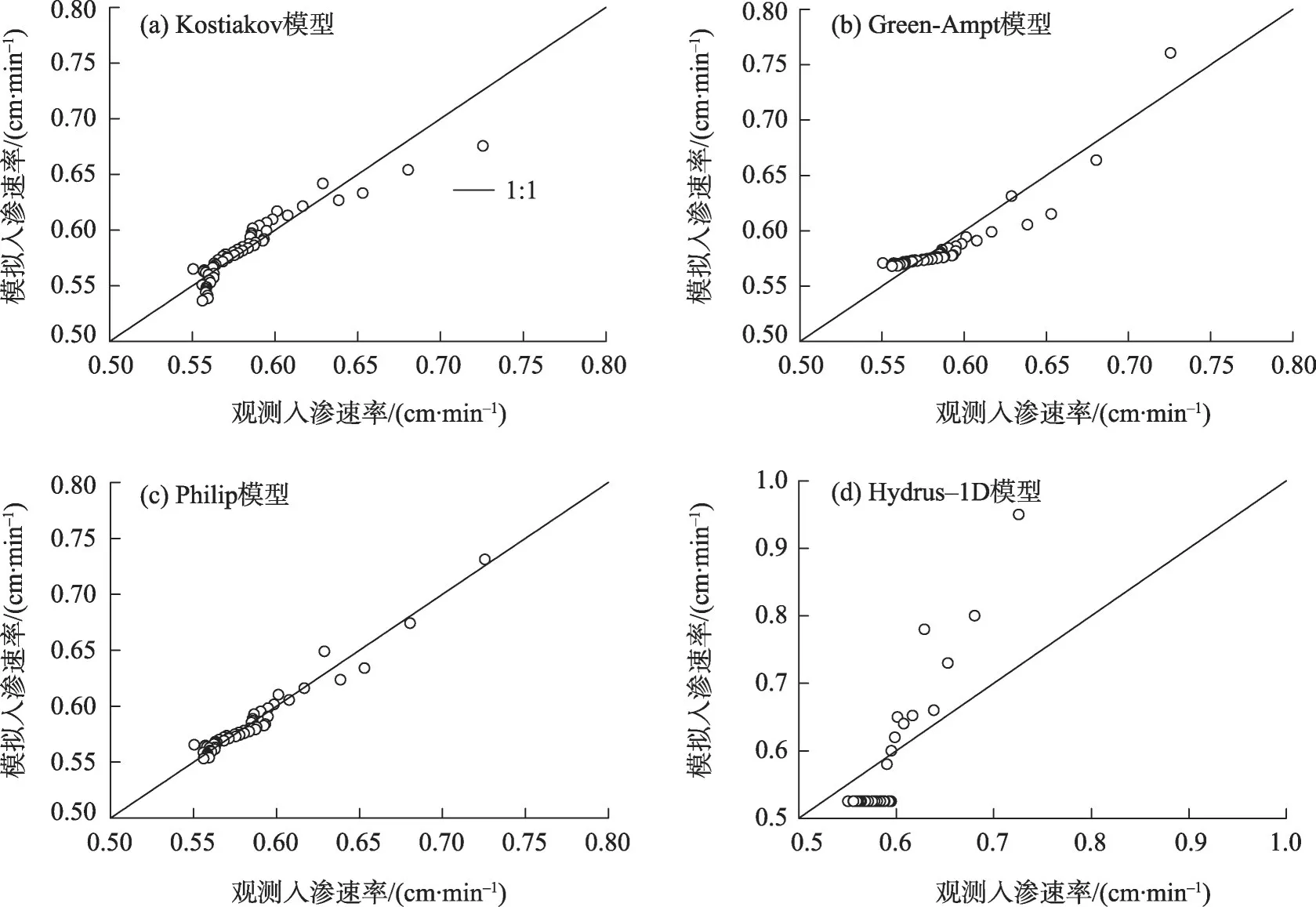
图5 入渗速率模拟值与实测值比较Fig.5 Comparison of simulated infiltration rate from models with observed result

3.2.2 累积入渗量 模拟与观测累积入渗量关系如图6 所示，结果表明，4 种模型累积入渗量模拟值均与实测数据有较好的相关性。而Philip 模型R2最高，RMSE 系数最低，Kostiakov 模型RMSE 次之（表3），但Hydrus-1D模型下RMSE值系数相对较高，表明高估了累积入渗量，尤其在入渗初期，但4种入渗模型R2系数均达到了0.98以上，因此，4种入渗模型均是预测砂土累积入渗量较为有效的模型，尤其是Philip模型。

表3 模拟结果拟合优度参数Tab.3 Goodness-of-fit parameters for simulation results with models

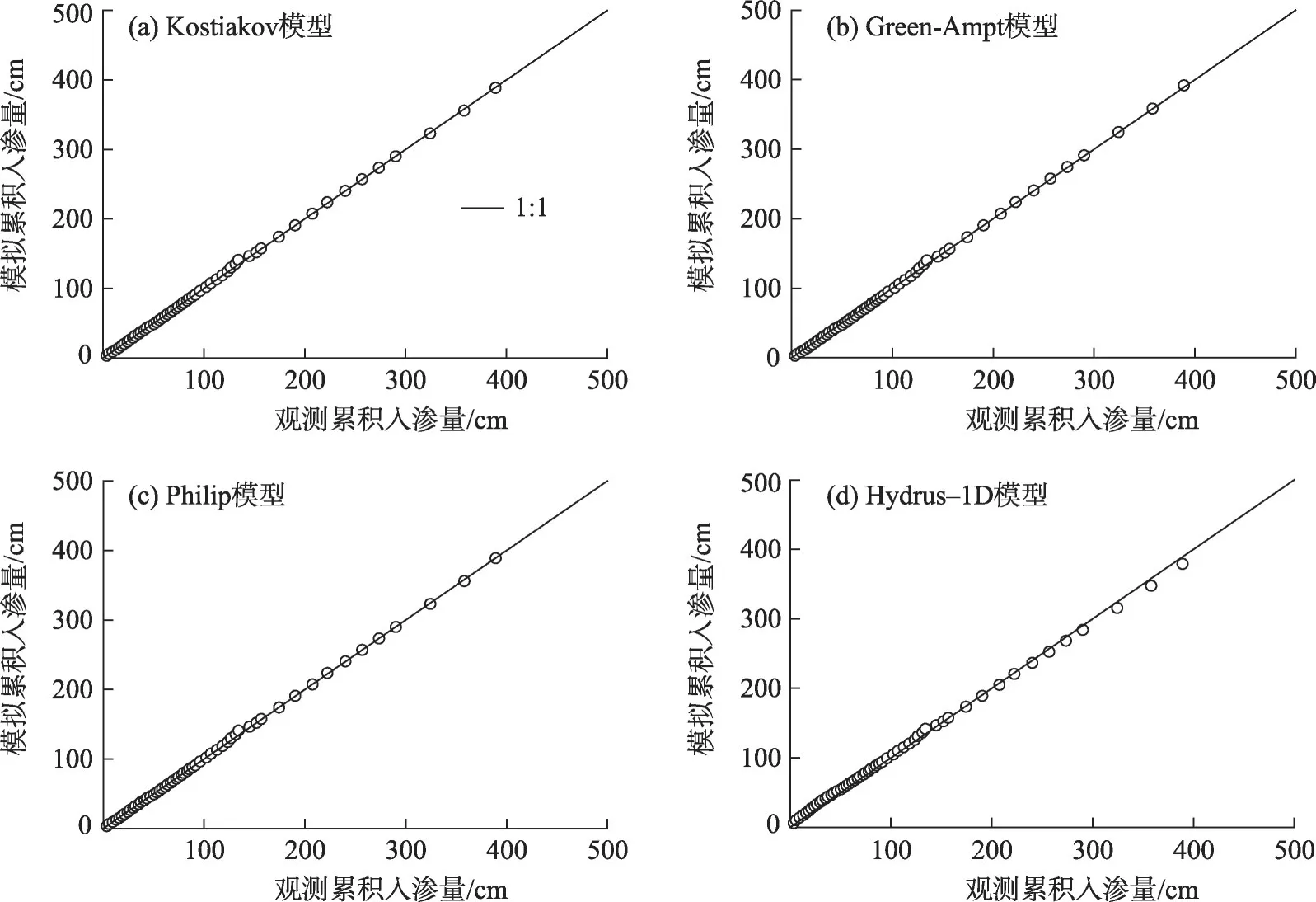
图6 累积入渗量模拟值与实测值比较Fig.6 Comparison of simulated cumulative infiltration from models with observed result

3.2.3 湿润锋距离 模拟与观测湿润锋距离之间的关系如图7 所示，结果表明，Green-Ampt 和Hydrus-1D模型的湿润锋距离模拟值与观测值差异较大，尤其是Hydrus-1D 明显高估了湿润锋推进距离，其均值R2小于Philip 模型。一种可能的解释是Hydrus-1D 忽略了土壤水侧渗和气流，以往研究表明，Hydrus-1D高估了湿润区的蓄水能力，但综合RMSE和R2均值结果可知，Philip模型对砂土湿润锋推进距离的预测效果较好。

图7 湿润锋距离模拟值与观测值比较Fig.7 Comparison of simulated wetting front depth from models with observed result

3.2.4 土壤含水量与Hydrus-2D 模拟 基于Hydrus-2D模拟土壤含水量如图8所示。结果表明，土壤水分模拟值与观测值拟合度较低，R2均值仅为0.82，尤其在表层0～10 cm，R2仅为0.65，综合0～80 cm的RMSE和R2均值结果可知，Hydrus-2D模型并不能很好地预测积水入渗条件下土壤水分变化过程。

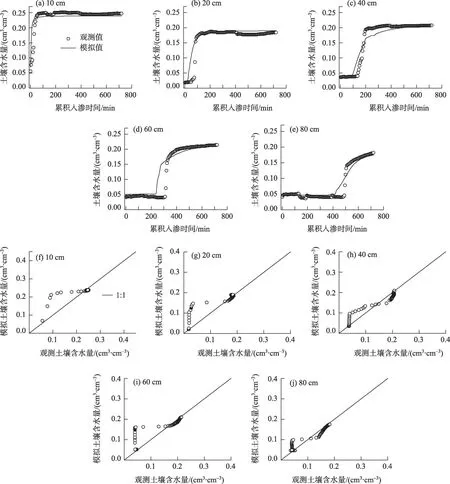
图8 基于Hydrus-2D模拟土壤含水量与实测值比较Fig.8 Comparison of simulated soil water content by Hydrus-2D model with observed result

3.2.5 土壤含水量与Hydrus-3D 模拟 基于Hydrus-3D 模拟土壤含水量如图9 所示，结果表明，土壤含水量模拟值与观测值基本一致，0～80 cm 土壤剖面的R2均值为0.93，RMSE 均值为0.02 cm3·cm-3（表4）。尽管较Hydrus-2D 相比，Hydrus-3D 对入渗后期土壤含水量预测较低，但是综合考虑R2和RMSE值，Hydrus-3D是描述和模拟砂土积水条件土壤含水量较为理想的选择。

表4 H ydrus-2D和Hydrus-3D模拟结果拟合度参数Tab.4 Goodness-of-fit parameters for simulation results between Hydrus-2D and Hydrus-3D

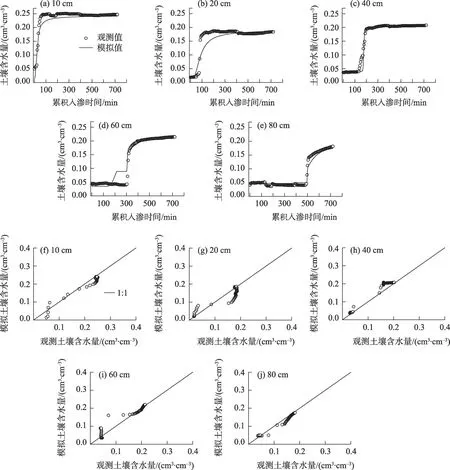
图9 基于Hydrus-3D模拟土壤含水量与实测值比较Fig.9 Comparison of simulated soil water content by Hydrus-3D model with observed result

4 讨论

4.1 土壤水分入渗特性

单环积水入渗仪是测量土壤水分入渗速率的最常用方法之一，已被广泛用于评估和监测降雨入渗进入土壤过程。研究表明，随着时间的延长，入渗速率随着入渗量的增加而降低，最终达到稳定入渗率［27］。本研究发现，砂土的稳定入渗率为0.55 cm·min-1，这与前人研究砂土入渗速率范围为0.2～0.77 cm·min-1结果相一致［28］，结果差异可能由于土壤质地、初始土壤含水量和地表覆盖条件导致。土壤水分运移过程中，非饱和区水分湿润锋推进动力学特性研究具有重要的意义，研究指出，单环入渗受环下水分横向运动影响，其基质势通量在湿润锋处占主导地位［29］，本研究发现湿润锋距离水平方向较垂直方向大。此外，在入渗发生的前100 min内，湿润锋推进速度随时间增加而减小，之后保持恒定不变（图10），一种可能的解释是砂土引发的漏斗流在水平方向上受基质势驱动，而在垂直方向上受重力势驱动。

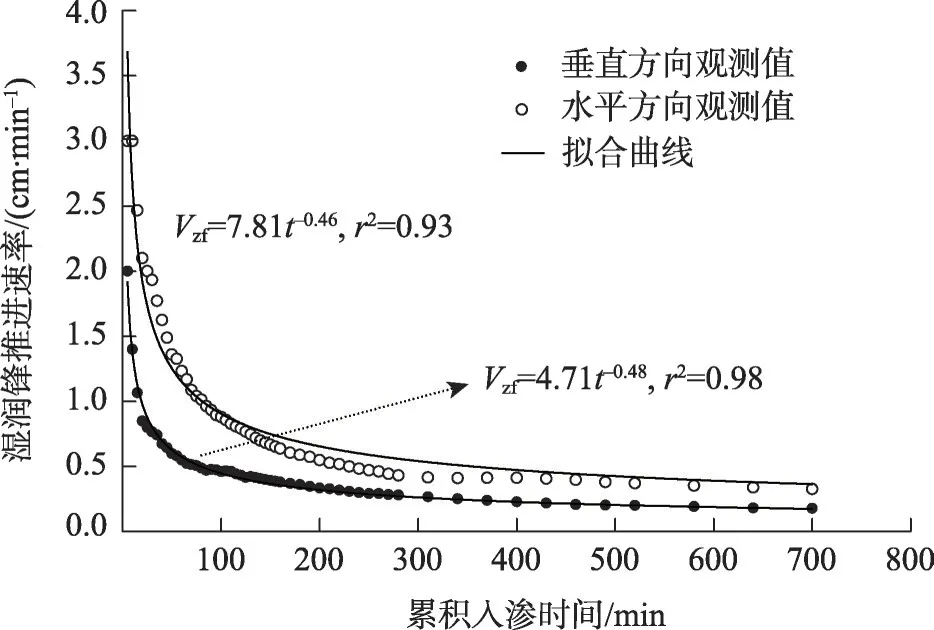
图10 垂直和水平两个方向湿润锋推进速度Fig.10 Comparison of observed the velocity of the wetting front with two directions

先前研究表明，Philip 模型可用于砂质土壤入渗速率与入渗时间关系预测［30］，Zolfaghari 等也做了类似报道［31］，然而，Duan等［28］和Ogbe等［32］通过研究入渗模型对砂土水分入渗适应性发现，Hortons模型较适宜累积入渗量预测，Wang等［13］通过模拟与实测值比较，证实Hydrus-1D 能够预测层状土柱砂土积水条件下的入渗速率。然而，由于模型参数和性能随土壤条件和时间的不同而存在差异，需要大量试验以确定入渗模型适用范围和条件。

4.2 土壤剖面水分状况

土壤水分分布状况是影响干旱区荒漠植物根系吸水有效性的重要因素，本研究结果表明，土壤含水量表层高于深层，积水入渗导致土壤水分在整个湿润区呈不均匀非饱和状态分布，这可能与土层结构对土壤的持水性能影响有关，尽管整个剖面土壤质地为砂土，但由于各层之间粒径组成比例有差异，导致持水性略有不同，出现土壤含水量空间变异［33-34］。此外，Hydrus-3D较Hydrus-2D对土壤含水量数值模拟结果效果最佳，其优点是考虑了水分在土壤中的三维变饱和多孔介质运动。

5 结论

以自然沙丘中的丘间低地为研究对象，通过单环入渗试验，以确定土壤水力参数，并分析了砂土在固定水头渗流区的土壤水分变化对入渗响应，以验证几种入渗模型在积水入渗条件下的适应性状况，取得以下主要结论：

（1）入渗初期入渗速率随时间急剧下降，之后趋于稳定，整个入渗过程中，水平湿润锋的推进速度较垂直方向快，入渗速率、累积入渗量和湿润锋深度与时间呈幂函数关系。

（2）受边界和初始条件以及土壤水力参数设置等因素影响，Hydrus-1D 水文模型在砂土水分入渗模拟中表现欠佳，但当前试验条件下，通过性能评价指标系数比较，特定土壤环境中Philip 较Green-Ampt、Kostiakov-Lewis 和Hydrus-1D 模型能够合理描述砂土入渗参数，反映较真实的土壤水动力过程。

（3）单环入渗试验需要同时考虑环内一维和环外三维水流过程，而Hydrus-3D 模型基本能反映砂土不同剖面三维土壤水分变化。总之，结合Philip和Hydrus-3D 水文模型确定砂土入渗是可行的，但此结果只是基于砂土，能否应用其他类型土壤水分入渗过程的评估有待进一步研究。