基于湿周法的济南山区中小河流生态流量研究
2022-02-10张叶魏俊黄森军王琦付意成张晶赵进勇
张叶 魏俊 黄森军 王琦 付意成 张晶 赵进勇
摘 要:为探讨湿周法在山区中小河流的适用性,以济南市西南部创新谷为例,基于湿周法中的斜率法,计算研究区河流干支流的生态流量,研究分析斜率法的适用性,并探讨在计算过程中典型断面的选取依据。经计算确定,北大沙河干流、大彦河干流、皇姑井村河干流和小刘河的生态流量依次为4.9、3.7、3.9、2.1m3/s。建议在利用湿周法进行山区中小河流生态流量的计算时,在结合当地水文资料的基础上,选择宽深比相对较小、横断面为抛物线形的河道断面作为典型断面。
关键词:生态流量;湿周法;河道断面;中小河流
中图分类号:X143;TV211.1+1 文献标志码:A doi:10.3969/j.issn.1000-1379.2022.01.019
引用格式:张叶,魏俊,黄森军,等.基于湿周法的济南山区中小河流生态流量研究[J].人民黄河,2022,44(1):89-93.
ResearchonEcologicalFlowofSmallandMedium SizedRiversinJinanMountainAreaBasedonWetCycle
ZHANGYe1,2,WEIJun3,HUANGSenjun3,WANGQi2,FUYicheng2,ZHANGJing2,ZHAOJinyong2(1.HebeiAgriculturalUniversity,Baoding071001,China;2.ChinaInstituteofWaterResourcesandHydropowerResearch,Beijing100038,China;3.PowerChinaHuadongEngineeringCorporationLimited,Hangzhou311122,China)
Abstract:Inordertodiscusstheapplicabilityofthewet periodmethodtosmallandmedium sizedriversinmountainareas,thisarticletook theinnovationvalleyinsouthwesternJinanasanexampleandbasedontheslopemethodinthewet periodmethod,calculatedtheecological flowofeachmainstreamtributaryinthearea,studiedandanalyzedtheapplicabilityoftheslopemethodanddiscussedtheselectionbasisof thetypicalsectioninthecalculationprocess.Throughcalculation,theecologicalflowsofthemainstreamofBeidashaRiver,themainstream ofDayanRiver,themainstreamofHuanggujingcunRiverandtheXiaoliuRiverweredeterminedtobe4.9,3.7,3.9and2.1m3/srespec tively.Itissuggestedthatwhenusingthewetcyclemethodtostudytheecologicalflowofsmallandmedium sizedriversinmountainousare as,basedonthecombinationoflocalhydrologicaldata,achannelsectionwitharelativelysmallwidth to depthratioandaparaboliccross sectionisselectedasthetypicalsection.
Keywords:ecologicalflow;wetweekmethod;channelsection;medium sizedrivers
1 引 言
近年来,随着水资源的大规模开发利用,河流自然水文情势发生了巨大变化[1]。水文情势的变化引起河流生态系统结构与功能的变化,甚至导致淡水生态系统严重退化[2]。为实现水生态环境的保护与修复,维持河流正常的自然与社会功能,满足生态服务需求,需要研究何种水文情势才能维系河流生态健康,从而引出生态流量的科学确定问题[3-5]。国内外学者在生态流量的推求和计算方面进行了许多研究,生态流量的计算方法大致可以分为4类:生态水文学法、水力学法、生境模拟法和整体分析法[2],每种方法各有特点和适用范围[6]。生态水文学法仅需历史水文数据,但过于概化河流情况,适用于野外监测较困难的河流;水力学法所需数据的获取相对简单,适用于较为稳定的河流;生境模拟法充分考虑了生物生存的适宜条件,适用于敏感期生态流量要求较高的河流;整体分析法系统考虑了河流生态系统的流量需求,但成本较高[7]。
我国先后出台了一些生态需水相关的导则、规范,对生态流量的概念与计算等进行了规定。2010年水利部发布《河湖生态需水评估导则(试行)》(SL/Z 479—2010),对Tennant法、90%保证率最枯月平均流量法、流量历时曲线法等水文学方法和湿周法、R2CROSS等水力學法进行了总结。2013年水利部发布《水资源保护规划编制规程》(SL613—2013),对生态需水满足程度评价及问题分析,生态需水对象及目标要求,生态需水保障的内容、技术方法和要求等进行了规定。2014年水利部发布《河湖生态环境需水计算规范》(SL/Z712—2014),澄清了河道湖泊生态环境需水的概念,给出了生态需水计算过程中应考虑的因素,建议河道内生态环境需水量采用水文综合法、分项功能法等方法计算。2015年水利部发布《河湖生态保护与修复规划导则》(SL709—2015),对生态需水保障、生态基流和敏感生态需水控制断面的拟定、生态需水量的确定、湖泊湿地生态水位的确定及分析方法、生态需水保障措施等进行了规定和建议。
在实际计算过程中,由于不同河流的水文资料、地形数据等不尽相同,因此不同河流、水系要根据实际情况选择合适的计算方法。根据河流所处区域位置、现场实际情况和水文资料,遵循科学性、代表性和实际可操作性原则,依据我国生态环境需水相关导则或指南[8-9],确定研究河段的生态流量。湿周法是水力学法中常用的一种方法,该方法以湿周为生态系统栖息地指标,建立湿周与流量的关系曲线,选取临界点所对应的流量作为生态流量[10]。确定临界点的方法有曲率法(曲率绝对值最大)和斜率法(斜率为1或其他设定值)。湿周与流量的关系主要有幂函数和对数函数关系[11],当符合幂函数关系时,相比曲率法,斜率法进行临界点的确定更适宜[12]。
肖玉成等[13]利用湿周法中的斜率法和曲率法对沣河的生态流量进行了研究。于鲁冀等[14]利用斜率法、曲率法和多目标评价法3种改进的湿周法计算了贾鲁河不同频率年河道内的生态需水量。吉小盼等[15]以西南山区岷江和大渡河为研究对象,利用斜率法、曲率法和经验法分析确定各断面最小生态需水量,从而研究了湿周法的适用条件及转折点的确定方法。笔者以济南创新谷为例,根据河道的实际情况,选用湿周法中的斜率法对区域内河流的生态流量进行计算与验证,并给出典型断面选取的建议。
2 研究区概况与方法
2.1 研究区概况
济南市西南部山区创新谷总体规划面积70km2,其中产业核心区20km2。创新谷属北大沙河流域,地势东南高西北低。北大沙河自东南向西北贯穿创新谷片区东北角,全长4.25km,自崮云湖水库下游进入创新谷,北流至长清湖,沿途有皇姑井村河、小刘河汇入。大彦河及其支流位于创新谷北部,往北流入长清湖,总长度2.705km。
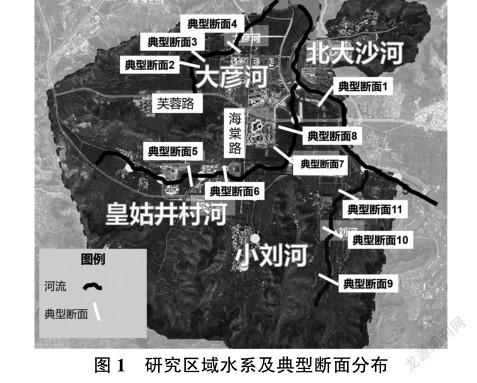
北大沙河是创新谷的骨干河道,但崮云湖水库截断其上游来水,导致研究区内河段水量不足,呈间断干涸状态。河岸两侧存在较宽河岸带,绿化程度较高,但是植被结构单一,景观性较差。大彦河现状河内无水,沟槽内杂草丛生,河槽边缘不明显。皇姑井村河干流发源于创新谷池子村西南部的山谷内,于大彦村东边汇入北大沙河,皇姑井村河及其支流为典型的山区季节性河流,枯水期河道断流、河床裸露,雨季流量明显增大。小刘河位于创新谷东南角,发源于钟庄村和小刘村南部山谷内,现状河道两岸高低起伏较大,沟道冲刷严重。为改善区域内河流现状,实现人水和谐,应科学确定其生态流量,满足其基本生态需水。本文依据收集的相关资料和现场实际踏勘结果,依次选取各河流典型断面,采用湿周法计算研究区河流生态流量。部分河流典型断面见图1,其中典型断面1位于北大沙河干流中游,典型断面2、断面3位于大彦河干流中游。经实地调研,断面1、断面2、断面3水流均匀、人类活动干扰较小,可以代表所在河流的实际状况。
2.2 研究方法

根据断面情况,通过以上公式计算相关参数,绘制湿周与流量关系曲线。
3 结果与讨论
3.1 计算结果
(1)北大沙河干流。依据地形数据绘制创新谷内北大沙河干流断面,考虑区域位置、水文资料等限制因素,选取研究河段中部断面进行计算。该断面形状为抛物线形,基于此断面建立湿周—流量关系曲线,选取关系曲线上斜率为1的点所对应的流量作为河道的基本生态流量,并且选取关系曲线的转折点所对应的流量进行对比、校核。北大沙河典型断面及Q—P关系曲线见图2。
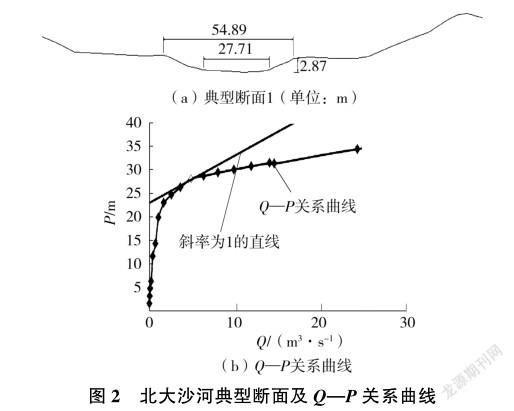
利用湿周法计算的北大沙河生态流量为4.9m3/s,流速为0.65m/s,水深为0.55m。经查询相关资料[16-20]和现场调研,北大沙河鱼类多为鲤科,尤以鲫鱼分布较为广泛,并在水深0.50m左右的位置观察到鲫鱼有较长时间的停留,因此认为北大沙河干流生态流量为4.9m3/s是合理的。
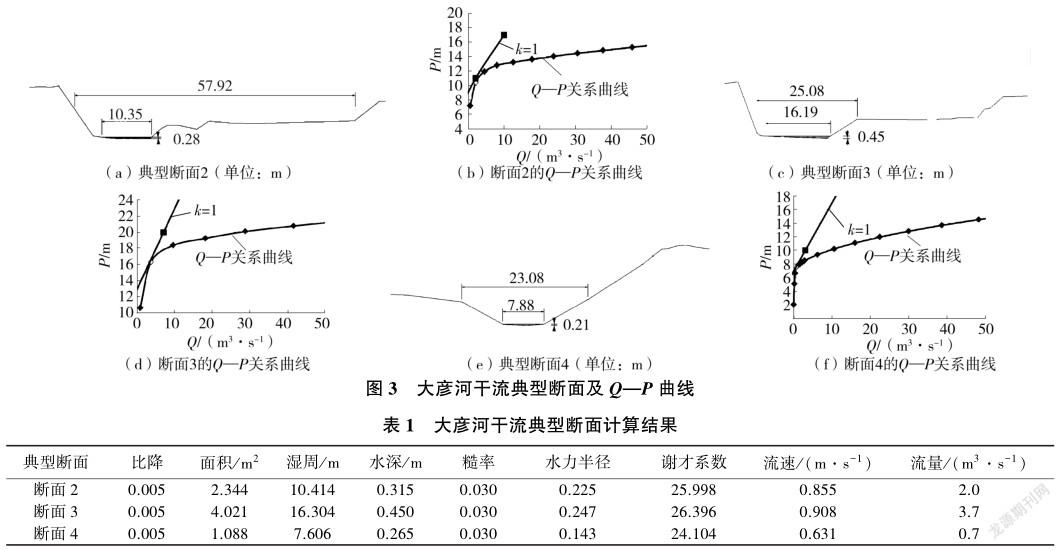
(2)大彦河干流。依据地形数据绘制大彦河干流各现状断面,在现状断面中选择位于大彦河干流中游拐弯处的典型断面2、断面3以及支流汇入口附近的典型断面4进行计算,3个断面为不规则断面,主河槽横断面分别为梯形、抛物线形和梯形,断面4上开口比前两个断面窄,见图3(k=1为斜率为1的直线)。基于以上断面建立湿周—流量关系曲线,将关系曲线上斜率为1的点所对应的流量作为河道基本生态流量,并且选取关系曲线上转折点所对应的流量进行对比、校核。大彦河干流Q—P关系曲线见图3,大彦河干流典型断面计算结果见表1。
由计算结果可知,典型断面4流量为0.7m3/s,与其余两个断面相差较大,结合当地实际水文资料和研究河段鱼类情况,认为该结果不具有代表性,不可作为此河段的生态流量;另外两个断面进行对比,水深0.450m接近0.50m,故认为大彦河干流生态流量应为3.7m3/s。
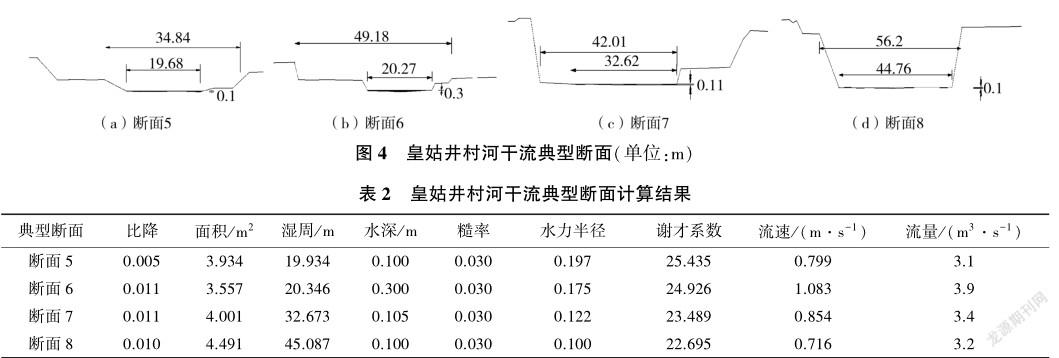
(3)皇姑井村河干流。皇姑井村河干流长4.952km,基于地形數据和现场踏勘,将中游和下游的典型断面5~断面8作为计算断面,其断面形状可分别概化为复式梯形断面、复式梯形断面、梯形断面、梯形断面,见图4。
皇姑井村河干流典型断面计算结果见表2,各断面流量计算结果相差不大,但水深相差较大。水深为0.300m的情况接近鲫鱼的最小生存水深0.50m,故认为皇姑井村河干流的生态流量应为3.9m3/s。
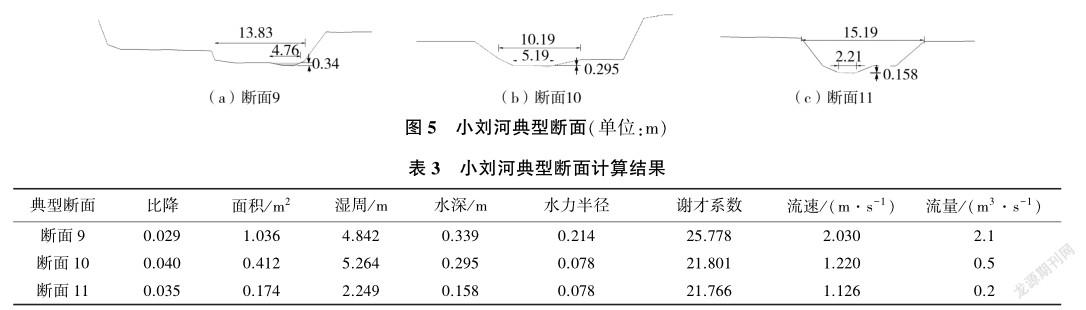
(4)小刘河。选择典型断面9~断面11进行计算,其均为不规则断面,主河槽断面形状分别可以概化为抛物线形、梯形、抛物线形,见图5。小刘河典型断面计算结果见表3,结合研究区域的代表鱼类,确定小刘河的生态流量为2.1m3/s。
3.2 讨 论
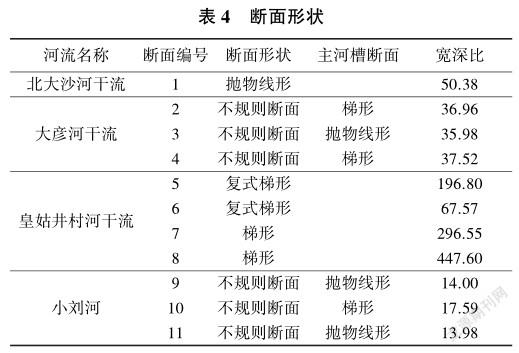
吉利娜等[10]以西南山区河流为研究对象,得出湿周法适用于近似抛物线形或矩形的断面,不建议用于近似三角形或梯形的断面。肖玉成等[13]以北方河道沣河为研究对象,得出直接利用湿周法计算生态流量对于水浅、宽深比特别大的河道,其结果会存在一定问题,即建立的湿周—流量关系曲线难以找到对应的临界点。对比北大沙河干流的典型断面1、大彦河干流典型断面3、皇姑井村河典型断面6和小刘河典型断面9,这4个断面为各自河道生态流量确定的典型断面,其相似之处为河道水流宽深比(水面宽与最大水深之比)相对较小,且断面形状主要为抛物线形和复式梯形,具体情况见表4。
基于上述分析,针对研究区的4条山区河流,其最终确定生态流量所依据断面形状依次为抛物线形、抛物线形、复式梯形和抛物线形。因此建议在利用湿周法进行山区中小河流生态流量推求时,在结合当地水文资料数据的基础上,综合考虑所选断面的稳定性,遵循代表性、易操作性、全面性、可行性、可靠性等原则,尽量选择抛物线形和复式梯形河道断面,且宽深比越小,断面越稳定,其结果越具有代表性。
4 结 论
依据计算结果,确定北大沙河干流、大彦河干流、皇姑井村河干流和小刘河的生态流量依次为4.9、3.7、3.9、2.1m3/s。根据已有研究结果,当湿周—流量关系符合幂函数关系时利用斜率法更适宜。经过对研究区域4条河流的计算分析,最终确定生态流量所依据的典型断面依次为断面1、断面3、断面6、断面9,分析其在推求生态流量过程中所得到的湿周—流量关系曲线,发现均符合和较符合幂函数关系。结合所选断面的宽深比,建议在利用湿周法进行山区中小河流生态流量的推求时,应考虑河道断面的稳定性,选择宽深比相对较小、断面形状为抛物线形的河道断面作为典型断面。
参考文献:
[1] 董哲仁,孙东亚,赵进勇,等.河流生态修复[M].北京:中国水利水电出版社,2013:21-38.
[2] 董哲仁,张晶,赵进勇.环境流理论进展述评[J].水利学报,2017,48(6):670-677.
[3] 乔钰,胡慧杰.黄河下游生态水量调度实践[J].人民黄河,2019,41(9):26-30,35.
[4] 李茜,尚潇瑛,赵敏歌,等.渭河陕西段健康评估研究[J].人民黄河,2019,41(5):77-81,85.
[5] 婁利华.河道适宜生态流量研究[J].水资源开发与管理,2018(10):35-39.
[6] 徐志侠,陈敏建,董增川.河流生态需水计算方法评述[J].河海大学学报(自然科学版),2004,32(1):5-9.
[7] 李洋.筑坝河流鱼类产卵生态流量研究[D].北京:中国水利水电科学研究院,2019:5-13.
[8] 王智林,熊北锋.无资料河流生态流量确定方法初探[J].陕西水利,2018(3):41-43.
[9] 高华永,代兴兰.黄泥河流域河道生态流量研究[J].人民珠江,2012,33(3):42-44.
[10] 吉利娜,刘苏峡,王新春.湿周法估算河道内最小生态需水量:以滦河水系为例[J].地理科学进展,2010,29(3): 287-291.
[11] CHRISTOPHERJG,MICHAELJS.UseofWettedPerimeter inDefiningMinimumEnvironmentalFlows[J].Regulated RiversResearchandManagement,2015,14(1):53-67.
[12] 尚松浩.确定河流生态流量的几种湿周法比较[J].水利水电科技进展,2011,31(4):41-44.
[13] 肖玉成,张新华,严瑞平,等.湿周法在超宽浅型河道生态需水计算中的应用[J].人民黄河,2010,32(10):87-88,90.
[14] 于鲁冀,陈慧敏,王莉,等.基于改进湿周法的贾鲁河河道内生态需水量计算[J].水利水电科技进展,2016,36(3):5-9.
[15] 吉小盼,蒋红.基于湿周法的西南山区河流生态需水量计算与验证[J].水生态学杂志,2018,39(4):1-7.
[16] 宋佳.济南城市河流鱼类群落结构及水生态健康评价[D].大连:大连海洋大学,2016:33-38.
[17] 谭璐,樊甜甜,郭伟,等.济南流域春季鱼类多样性研究及水体健康评价[J].河北渔业,2016(3):18-21.
[18] 姜庆生.北方地区鲫鱼养殖技术要点[J].黑龙江水产,2019(4):42-43.
[19] 严丽.鲫鱼养殖技术及病害防治要点[J].江西水产科技,2019(2):16-17.
[20] 陈一良,荆丹丹,岳一莹,等.沼液养鱼水质变化及鲫鱼适应性研究[J].江苏农业科学,2019,47(6):148-151.
【责任编辑 吕艳梅】
