基于蒙特卡罗方法的复合材料辐射屏蔽设计

白鸿伟，李 达，郭 寻,3，薛云飞，靳 柯,3

(1.北京理工大学材料学院，北京 100081；2.国家核安保技术中心，北京 102413；3.北京理工大学前沿交叉科学研究院，北京 100081)

乏燃料后处理是实现核燃料循环、确保核能可持续发展的关键途径[1]。在乏燃料后处理尾端，钚废料发生自发裂变反应会产生大量高能中子。高能中子经过屏蔽设施的慢化、散射、吸收过程后，在外层控制区(如黄区[2])中工作人员面临的主要是低能中子和中低能γ射线的辐射威胁。穿戴防护服或防护用具是一种减少工作人员承受剂量的有效手段。针对中子屏蔽材料的研究已经较为深入[3]，但将其实际应用于防护服或防护用具时需考虑其对使用环境中多种射线的混合屏蔽能力。

早期辐射屏蔽材料的问题在于屏蔽效果单一，难以面对后处理厂外层控制区内低能中子和γ射线等此类多种射线混合辐射环境。因此开发具备多种射线综合屏蔽和优异力学性能的复合材料对于研发新型辐射防护用具、减少工作人员承受剂量具有重要意义。

目前常见的中子和γ射线综合屏蔽材料有不同功能填料无纺布型、无机粒子填充聚合物和皮芯状纤维复合聚合物等。利用功能填料和多层无纺布制得中子复合材料的辐射屏蔽率高、生产工艺简单，但使用重金属铅存在危害人体健康的风险[4]。利用无机粒子填充聚合物复合材料制作的面料具备良好的柔韧性、透气性等，但热中子屏蔽性能不足[5]。

皮芯状中子屏蔽纤维的典型代表为硼纤维。硼纤维一般指采用化学气相沉积法将元素硼沉积到钨丝等基体上所制得的复合型纤维。天然硼资源丰富，价格低廉，且热中子吸收截面较大，是一种较为理想的中子屏蔽材料。而重金属钨的纤维基体可以使纤维兼具一定的γ射线屏蔽能力。此外，钨/硼纤维为单丝纤维，具有高强度、高模量和低密度等优点[6]。通过控制脆性硼在纤维中的占比，使其具有一定的可弯折度，可用于辐射屏蔽织物的编织。因此，本文以其为主体屏蔽组元，构建了一种钨/硼纤维增强聚合物复合材料，评估其对于中子-γ射线混合辐射的屏蔽效果。

Geant4是一个由欧洲核子研究组织(CERN)开发的，基于蒙特卡罗方法模拟物质中粒子运输的软件包，因其开源性、通用性和可扩展性被广泛应用于核物理、医学物理和辐射屏蔽等领域[7-9]。Geant4是目前欧洲航天局用于详细辐射传输分析的标准蒙特卡罗代码，其计算过程中使用的相关参数均来自于实验数据，因此在模拟中子和γ射线等粒子输运方面具有较高的可靠性。

本文以后处理厂控制区内低能中子-γ射线混合辐射为典型辐射环境，分析了一种皮芯状钨/硼纤维增强聚合物复合材料的屏蔽设计方法。结合国家标准《放射事故个人外照射剂量估算原则》(GBZ/T 151—2002)[10]和《用于光子外照射放射防护的剂量转换系数》(GBZ/T 144—2002)[11]，利用Geant4程序分别模拟计算了复合材料中纤维层数、层内纤维间距和基体填隙物占比等参数对热中子和低能γ射线的剂量屏蔽率以及混合剂量屏蔽率的影响，其中混合剂量屏蔽率考虑了硼在吸收低能中子时放出的次级γ射线。通过研究各材料参数对复合材料综合辐射屏蔽效果的影响，为该复合材料在综合辐射防护领域的应用提供参考。

1 复合材料辐射屏蔽蒙卡计算

1.1 复合材料辐射屏蔽计算模型的建立

利用Geant4程序构建辐射屏蔽计算模型，主要包括粒子源的设定、复合材料的建模和探测器的设定三部分，如图1所示。

图1 两种钨/硼纤维增强含硼/铋聚合物的辐射屏蔽计算模型Fig.1 Two models of radiation shielding calculationfor polymers containing boron/bismuthenhanced by tungsten/boron fibers

(1)粒子源设定

粒子源均假定中子和γ射线以面源形式垂直入射材料表面，如图1中红色箭头所示。由于无法精确得到后处理厂黄区环境中的中子和γ射线注量率或粒子能谱，因此，本文首先简要评估了复合材料对几种具有代表性的中子和γ射线的屏蔽能力，中子源分别选择0.025、0.5 eV的单能热中子和热中子能谱(麦克斯韦谱)；γ射线源分别选择50、150和250 keV的单能γ射线。之后，在研究不同材料参数对复合材料辐射屏蔽率的影响时粒子源均为热中子能谱和150 keV单能γ射线。为了使屏蔽计算结果具有较好的统计性，本文使用的中子和γ射线注量均为108/cm2。

(2)复合材料模型的建立

复合材料的建模主要包括材料的定义和物理过程的调用，而材料的定义包括钨/硼纤维和基体材料两部分。

如图1所示，模拟单元为1 mm×1 mm×1 mm的立方体，队列排布的圆柱体代表插入基体的钨/硼纤维，本文考虑了层间纤维平行和层间纤维垂直两种纤维排布方式，其中，层间纤维平行状态特指层间纤维为对齐状态的情况，即层间纤维无错排。圆柱体中心黑色圆柱为钨芯，外层深蓝色区域为天然硼。本文的屏蔽计算均设定钨/硼纤维中钨芯的直径为14 μm，包覆硼外径为54 μm。淡蓝色区域代表复合材料基体，由碳、氢等元素组成的有机聚合物构成，对低能中子或γ射线的屏蔽效果影响基本可忽略不计。

不同粒子与材料相互作用的形式不同，需依据不同粒子源调用相应的物理过程。对于中子主要调用中子弹性散射、中子吸收截面等数据，使用的物理模型为QGSP_BIC_HP；对于γ射线主要调用光电吸收和康普顿散射截面等数据，使用的物理模型为standard模型。

(3)探测器设定

在复合材料右侧设置探测器以接收穿过复合材料的剩余粒子以及射线与材料相互作用产生的新粒子(如次级γ射线)，如图1绿色板材所示。通过对探测器中输出的粒子类型、能量和位置等信息进行统计，即可得到剩余粒子的强度及其分布，从而计算复合材料的辐射屏蔽效果。

1.2 辐射屏蔽计算

本文中计算的复合材料屏蔽能力均依据复合材料对有效剂量的衰减。对中子而言，注量与有效剂量之间具有直接转换关系，转换系数依赖于中子能量。在照射几何条件为旋转(ROT)的情况下，0.025 eV的中子对应的转换系数为4.6×10-12Sv·cm2。由于《放射事故个人外照射剂量估算原则》附录D没有更小中子能量对应的转换系数，因此，后续计算中默认能量低于0.025 eV的中子与0.025 eV中子对应的转换系数相同。对光子而言，注量与个人有效剂量的转换需要通过自由空气比释动能(Ka)进行间接转换。注量与Ka和个人剂量当量(Hp)与Ka的转换系数均依赖于光子能量。对于150 keV的单能γ射线，注量与Ka之间的转换系数为0.599 pGy·cm2，Hp与Ka之间的转换系数为0.892 Sv/Gy。硼吸收中子产生次级γ射线能量约为477 keV，注量与Ka之间的转换系数约为2 pGy·cm2，Hp与Ka之间的转换系数约为0.813 Sv/Gy。因此，分别统计屏蔽前后所有粒子对人体的有效剂量，即可得到复合材料对热中子和γ射线的辐射屏蔽率以及混合辐射屏蔽率。

均一材料的屏蔽效果主要取决于屏蔽组元的吸收截面、材料厚度和密度等。而对纤维复合材料而言，纤维的构型、占比和排布方式等也会影响最终屏蔽效果。为了分别研究纤维层数、层内纤维间距、纤维排布方式和基体填隙物等参数对复合材料屏蔽性能的影响，我们采用控制变量的方法。首先比较复合材料对不同能量中子和γ射线的屏蔽效果差异；之后以热中子和150 keV的单能γ射线为典型粒子源，逐渐增加纤维层数，研究复合材料整体辐射屏蔽率以及单位厚度辐射屏蔽率随纤维层数的变化；固定纤维层数，当纤维编织存在一定层内纤维间距(即存在孔隙)时，研究复合材料辐射屏蔽率随层内纤维间距的变化；此外，在不同层内纤维间距的条件下，对比纤维在基体中的两种排布方式对复合材料辐射屏蔽率的影响；最后，考察了在基体中加入一定质量分数的填隙物对于复合材料辐射屏蔽率的提升效果。

2 结果与讨论

2.1 纤维层数

在层内纤维无间距、层间纤维平行排布和基体不掺杂填隙物的条件下，评估了不同纤维层数的复合材料对几种不同能量中子源和γ射线源的辐射屏蔽率，如图2所示。由于热中子能谱的低能部分占比相对较高，因此，相比于0.025 eV的单能中子，其更易被屏蔽。随着中子或γ射线能量的提高，复合材料的辐射屏蔽率下降明显。例如，1层纤维复合材料对0.025 eV单能中子的辐射屏蔽率约为38.0%，而对0.5 eV单能中子的辐射屏蔽率明显下降至14.0%；1层纤维复合材料对50 keV单能γ射线的辐射屏蔽率约为4.8%，对150 keV单能γ射线的辐射屏蔽率下降至2.2%。后续计算复合材料对辐射的屏蔽时使用的粒子源均为热中子能谱和150 keV单能γ射线。

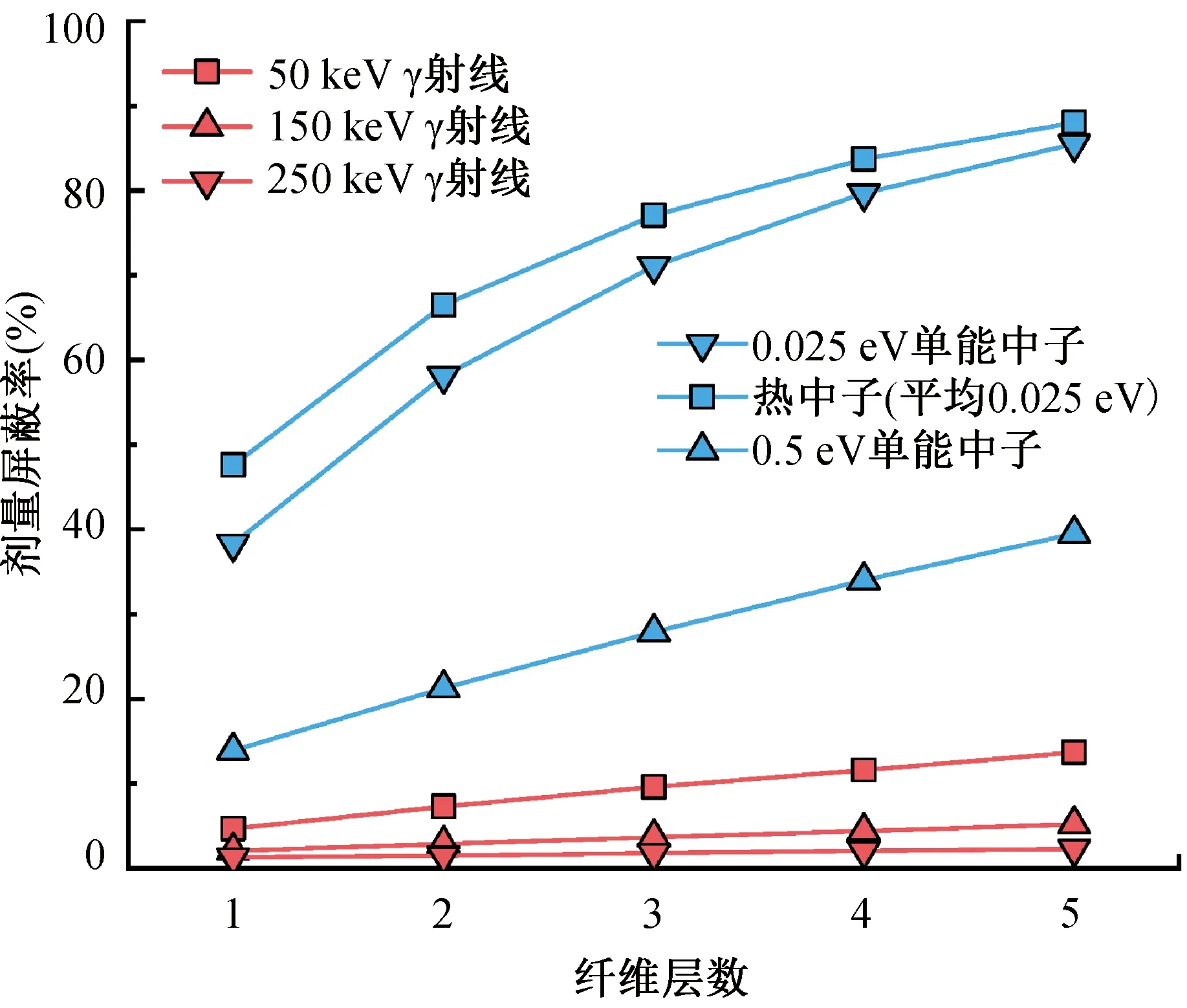
图2 复合材料对不同能量中子和γ射线的辐射屏蔽率对比Fig.2 Comparison of the radiation shielding rate ofcomposite materials towards neutron andγ-rays of different energy

在层内纤维无间距、层间纤维平行排布和基体不掺杂填隙物的条件下，以热中子能谱和150 keV单能γ射线为粒子源，分别统计了含1、2、3、4、5层纤维的复合材料对热中子和γ射线的辐射屏蔽率，并计算了混合辐射屏蔽率，如图3(a)所示。随着纤维层数的增加，复合材料对中子和γ射线的辐射屏蔽率均有显著增长。由于纤维中硼的含量占比较大，中子的辐射屏蔽率增长更为显著。材料中硼的总质量增加，硼吸收热中子的能力增强，产生次级γ射线的剂量呈上升趋势。但相对于中子剂量而言，量级较小，对整体屏蔽率影响不大。

在实际应用中，由于使用和成本的需求，纤维层数和整体材料厚度的增加不仅会造成织物力学性能及舒适性等劣化，还会导致单位厚度材料的屏蔽收益率持续下降。依据实际织物厚度，我们假定纤维层与相邻纤维层的间距为200 μm，据此统计了不同纤维层数下复合材料的单位厚度辐射屏蔽率，如图3(b)所示。随着纤维层数的不断增加，单位厚度复合材料的屏蔽率持续下降，即花费相同成本所能取得的屏蔽效果越来越差。目前纤维增强聚合物基复合材料所能达到的单位厚度辐射屏蔽率在40%/mm以上[12]，因此我们认为当单位厚度辐射屏蔽率低于此值时，设计的复合材料将不再具有良好的成本收益率。

图3 复合材料中纤维层数对中子和γ射线辐射屏蔽率的影响Fig.3 Effect of the number of fiber layers in composite materials on theradiation shielding rate of neutrons and γ-rays

2.2 层内纤维间距

保持层间纤维平行排布与基体不掺杂填隙物的条件不变，分别以含1、3、5层纤维的复合材料为研究对象，模拟计算层内纤维间距分别为10、20、30、40、50 μm时复合材料对辐射的屏蔽率，结果如图4所示。在三种纤维层数条件下，复合材料对中子和γ射线的屏蔽变化趋势相似。随着层内纤维间距的增加，孔隙率增加，相同体积内纤维占比减小，穿过复合材料的粒子占比增加，因此复合材料对中子和γ射线的屏蔽率均呈下降趋势。在含5层纤维条件下，复合材料层内纤维间距从10 μm增加到20 μm时，复合材料对中子的屏蔽率从75.0%降至64.0%，对γ射线的屏蔽率从4.5%降至4.0%，混合屏蔽率从60.0%降至51.0%。因此，在满足力学和使用等性能的情况下，尽可能减小层内纤维间距以降低孔隙率，可以提高复合材料的辐射屏蔽效果。此外，对比三种纤维层数的复合材料的辐射屏蔽率随层内纤维间距的下降趋势，可以得出随着纤维层数的增加，层内纤维间距对辐射屏蔽率的影响更为显著。

图4 不同纤维层数的复合材料中层内纤维间距对辐射屏蔽率的影响Fig.4 The effect of space between fiber layer on the radiation shieldingrate in composites with different fiber layers

2.3 纤维排布方式

在5层纤维和基体中不掺杂填隙物的条件下，分别模拟计算了层内纤维间距为10、30、50 μm时层间纤维平行和垂直两种纤维排布方式的复合材料屏蔽热中子后剩余中子的通量分布，考察排布方式对复合材料辐射屏蔽效果的影响。将模拟区域沿粒子入射方向投影到二维平面并划分为20×20的网格，作出剩余中子通量分布热图，如图5所示，入射前热中子通量均为108/cm2。从图中可以看出，层间纤维垂直排布方式的复合材料屏蔽热中子后剩余中子的通量更低且较均匀分布。

图5 不同层内纤维间距下两种纤维排布方式的复合材料对热中子的辐射屏蔽效果Fig.5 The radiation shielding effect of the compositematerials with two fiber arrangements in differentspaces between fiber layers on thermal neutrons

统计落在每个网格区域内的中子数目，定量比较两种排布方式的复合材料屏蔽热中子后剩余中子的平均通量与最大、最小通量，如图6所示。可以直观看到，其他条件相同时，层间纤维垂直排布方式的复合材料屏蔽热中子后剩余中子的平均通量要低于层间纤维平行排布。此外，相比于层间纤维平行的排布方式，层间纤维垂直排布方式的复合材料屏蔽后剩余中子的峰值通量偏离平均通量的程度更小，减弱了平行排布方式可能引起局部区域中子通量过高的问题。

图6 不同层内纤维间距下，穿过两种纤维排布方式的复合材料后剩余中子通量对比Fig.6 Comparison of the remaining thermal neutronflux after passing through the composite materialswith two fiber arrangements in differentspaces between fiber layers

2.4 基体填隙物

为了进一步提高复合材料的辐射屏蔽能力，考虑在聚合物基体中掺杂一定质量分数的天然硼和铋。在基体中掺杂硼和铋填隙物，一方面可以进一步提升复合材料的辐射屏蔽性能，另一方面可以减弱层内纤维间距和纤维排布方式引起的部分区域承受剂量较大的问题。在5层纤维、层间纤维垂直排布和层内纤维无间距的条件下，计算基体掺杂一定质量分数的硼与铋后复合材料的剂量屏蔽率如图7(a)所示。可以看出，随着基体中硼和铋含量的增加，复合材料对中子和γ射线的屏蔽能力均得到了显著提高。掺杂20%质量分数的硼、40%质量分数的铋使中子剂量屏蔽率由89.0%提升至97.6%、使γ射线剂量屏蔽率由5.4%提升至21.9%。图7(b)为掺杂不同质量分数硼和铋后透过复合材料的剩余中子空间分布，验证了基体中掺杂硼和铋后复合材料对中子的屏蔽能力显著提升。

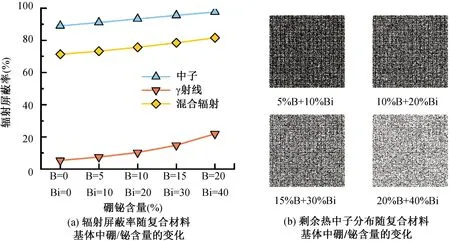
图7 基体含不同质量分数硼和铋的复合材料对中子和γ射线的辐射屏蔽率对比Fig.7 Comparison of radiation shielding rate of neutron and γ-rays of composite materialswith different mass fractions of boron and bismuth in the matrix

在上述的屏蔽计算过程中，结果均显示γ射线的屏蔽比热中子更为困难。因此，后续可以考虑提高纤维中钨的占比，以平衡热中子和γ射线的屏蔽效果。本文研究了复合材料中不同参数对屏蔽低能中子和γ射线剂量的影响，在此基础上，依据实际应用环境中特定粒子能谱及注量率，我们可以结合所需的屏蔽要求，合理调整材料参数，结合力学性能测试等实验对材料参数进一步反馈调整，最终设计得到混合屏蔽性能与结构/力学性能最优化的纤维复合材料。

3 结论

本文利用基于蒙特卡罗方法的Geant4程序设计了一种含硼/铋聚合物的钨硼纤维复合材料，设计的重点在于评估复合材料的组成和结构参数对复合材料屏蔽性能的影响。模拟结果表明，随着钨/硼纤维层数的增加，复合材料对热中子和低能γ射线屏蔽能力增长的趋势变慢，且单位厚度复合材料的屏蔽效率逐渐下降；尽量减少层内纤维的间距可以降低复合材料孔隙率，提升屏蔽效果；相比于层间纤维平行排布方式，层间纤维垂直排布方式的复合材料屏蔽中子后剩余中子剂量更低，且一定程度上减弱了局部区域剂量过高的问题；在基体中掺杂硼和铋可以进一步提高复合材料屏蔽效果并改善辐射剂量分布不均的问题。后续可以结合力学性能测试、屏蔽性能测试等实验以及成本评估进一步验证和优化复合材料的设计，有望为防护服的新型复合材料设计提供参考。