吊钉抗拔锚固性能试验研究及有限元分析
2022-02-10常世涛孙波魏树浩
常世涛,孙波,魏树浩
(北京市燕通建筑构件有限公司)
1 引言
预埋吊钉因其方便操作而受到广泛应用,然而目前国内没有对此类吊装配件的设计原则给予直接规定,对吊装配件的机理性研究相对较少。国内设计及分析大多根据《混凝土结构后锚固技术规程》JGJ145-2013[1]中锚栓的计算方法,但在结构形式、尺寸以及施工方法上存在一定的差异[2]。吊装现场大多根据工程经验,以此会给工程施工带来部分隐患。本文对预埋在混凝土中的吊钉力学性能进行了试验研究,在此基础上,建立了相应的有限元分析模型,对预埋吊钉受力性能进行了分析。
2 试验设计
2.1 试件设计
试验共设计4个试件,置于4个混凝土板之上。其布置如图1a所示。吊钉高度为170mm,直径为14mm,顶部直径为25mm,底部直径为34mm,钢材采用S355J0基材(详细尺寸如图1b所示)。混凝土板尺寸为700mm×700mm×250mm,底部单层双向钢筋12@150mm,钢筋强度等级为HRB400,保护层厚度30mm,混凝土强度为C40,吊钉埋深为140mm和100mm,试件主要参数见表1所示。
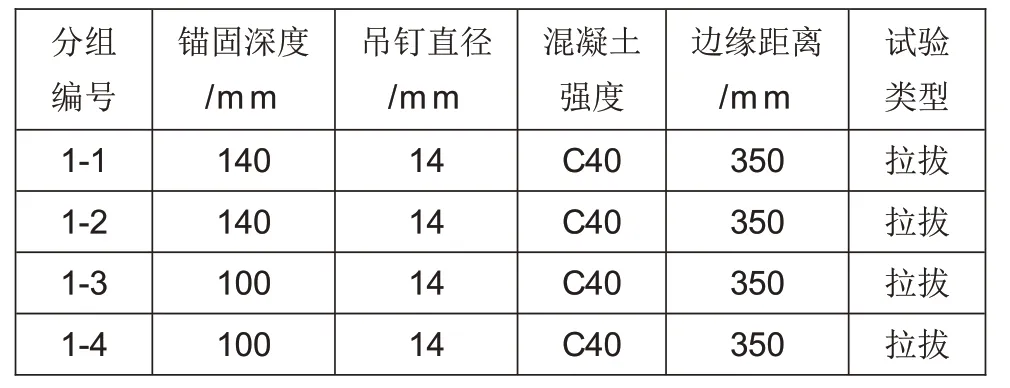
表1 试件主要参数
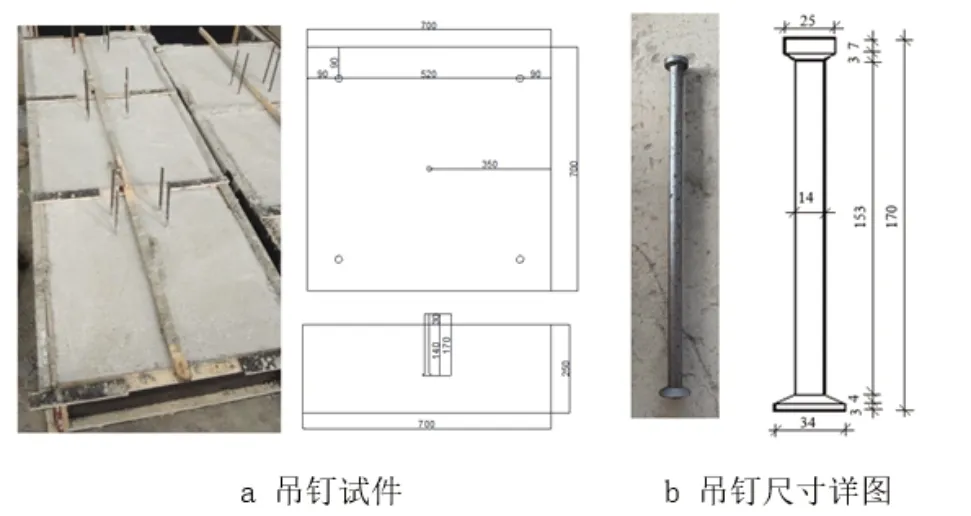
图1 吊钉尺寸及试件尺寸图
C40混凝土中水泥采用普通硅酸盐水泥,强度等级43MPa,粗骨料类型碎石,细骨料采用中砂,砂率为0.31,水灰比为0.39,设计配合比为m水:m水泥:m砂:m石子=0.39:1:1.29:2.88。在浇筑混凝土时,留置1组混凝土标准试块,并进行同条件养护。测得混凝土立方体抗压强度平均值分别为48.2MPa。采用标准试验方法针对吊钉钢材进行拉伸试验,钢材的屈服强度为429MPa、抗拉强度556MPa,延伸率为29%。
2.2 加载方案
试验加载采用自平衡装置。加载装置采用ZY型锚杆拉力机加载,加载设备量程为300kN。采用荷载大小控制方法分级加载。抗拔试验装置中,为避免1.5倍埋深范围内的混凝土受影响。
试验为单向静力加载,在加载前,先施加一个不超过预估极限荷载5%的预加荷载,消除试验装置或紧固件间的空隙,每级荷载值取为各组试件预估极限荷载的10%,当混凝土发生崩裂、吊钉拉断或者千斤顶无法持荷时,表明试件破坏,停止试验(见图2)。

图2 抗拔试验装置
2.3 量测内容
试验中测量了加载点的荷载大小F和吊钉位移变化s,加载点荷载大小通过千斤顶数字显示器直接读取,吊钉位移变化通过百分表量测,百分表量程为10mm。
3 试验结果及分析
3.1 极限承载力
表2中给出了各构件极限承载力大小及最终破坏形态,由表2可知,试件破坏形态均为钢材破坏,吊钉屈服荷载大约为60kN,极限承载力大小约为83kN,吊钉的安全系数大约为3.3,符合文献[3]中对与吊装构件安全系数的要求(见图3)。
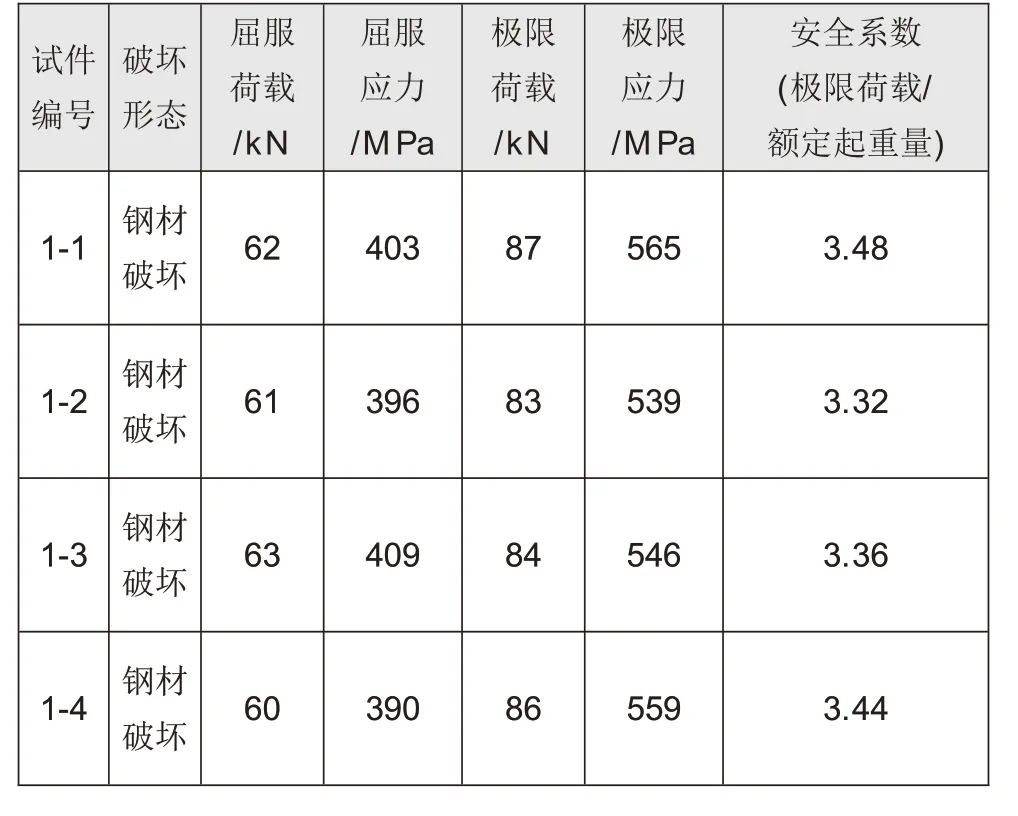
表2 试件极限承载力

图3 钢材破坏形态
3.2 试件破坏形态
对于试件1-1,随着荷载的不断增大,在吊钉根部垂直于混凝土边缘方向出现混凝土的裂缝,随着荷载的不断增大,裂缝逐渐向混凝土侧面发展。同时,吊钉进入屈服阶段,并逐渐出现径缩现象,试件最终破坏形式为吊钉拉断破坏。
对于试件1-2当荷载增大至66kN时,在吊钉根部出现微小裂缝,随着荷载的不断增大,裂缝不断向径向发展,裂缝宽度不断增大,当荷载达大到71kN时,吊钉出现明显的颈缩现象,其最终破坏为吊钉被拉断。
ACI318-05[4]中规定,对于预埋在混凝土中带撑帽的预埋吊装件,考虑有效埋深、混凝土强度、边缘距离,以及吊装件尺寸等因素的影响,发生的破坏形态包括混凝土锥体破坏、钢材破坏以及混凝土边缘拉崩破坏。根据文献中的公式,分别对不同破坏形态的承载力进行计算。根据表3中的计算结果可知,由于混凝土强度及埋深均较大,预埋吊钉发生混凝土锥体破坏承载力均大于钢材破坏承载力。同时,表4给出了计算承载力与试验结果对比,根据表3和表4计算结果可知,吊钉均发生钢材破坏与试验结果相同,规范承载力计算值与试验值吻合较好。
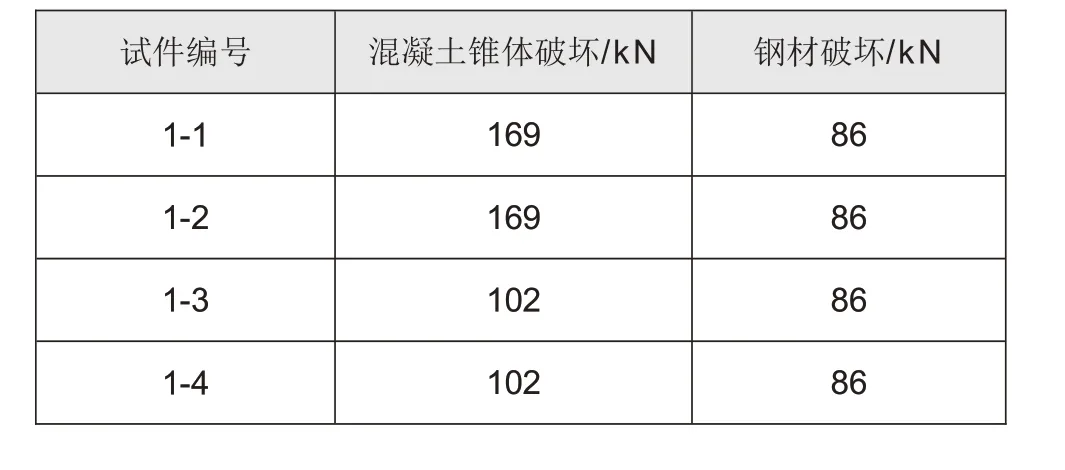
表3 吊钉各破坏形态承载力大小
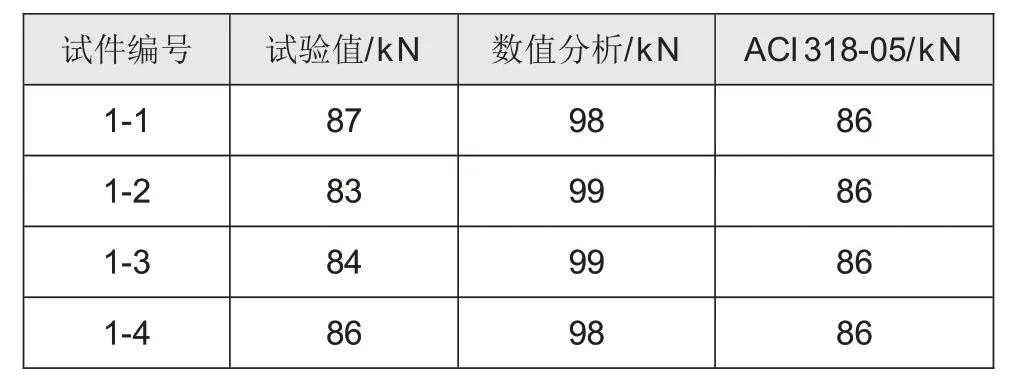
表4 试件极限承载力对比
3.3 试件荷载-位移曲线
由图4可知,加载初期,荷载-位移曲线基本上呈现出直线,吊钉处于弹性阶段,当荷载增大至60kN左右时,吊钉刚度发生明显变化即进入屈服阶段,当荷载增大至80kN左右时,吊钉截面发生明显的径缩或者拉断,构件发生破坏,构件的荷载-位移曲线与钢材基本相同。
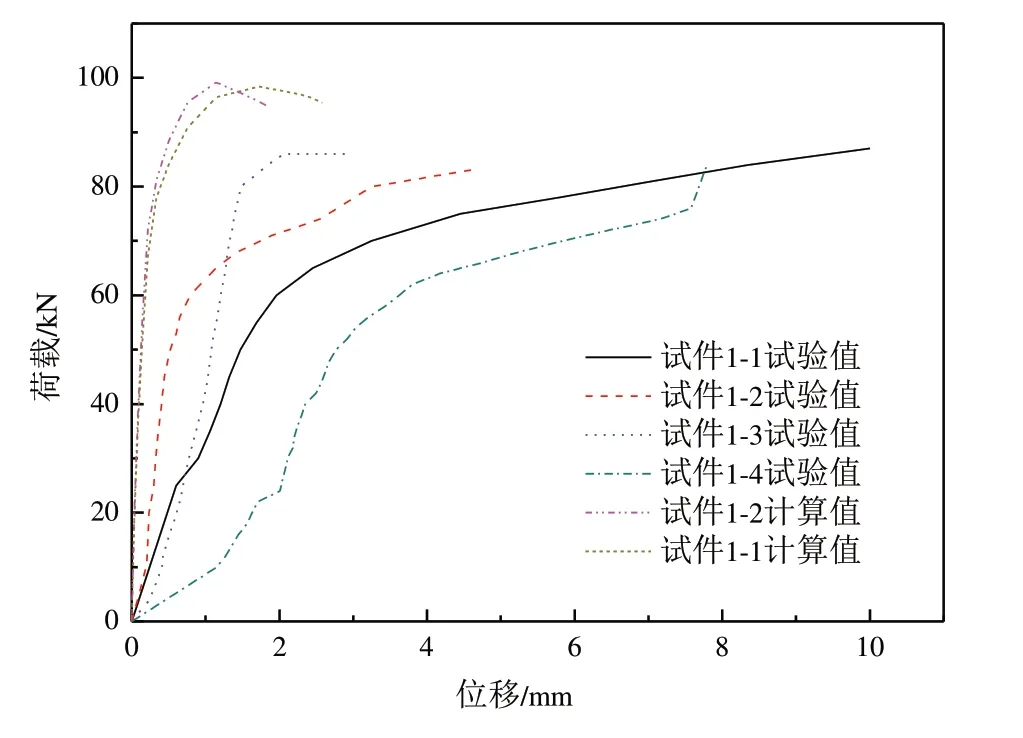
图4 试件荷载-位移曲线
4 力学性能分析
4.1 材料本构模型
钢材和混凝土材料强度根据材性试验结果确定。钢材的本构采用理想弹塑性模型,如图5a所示,图中,E为钢材的弹性模量,fy为钢材的屈服强度,混凝土本构采用文献[3]中混凝土应力-应变曲线关系,如图5b所示。
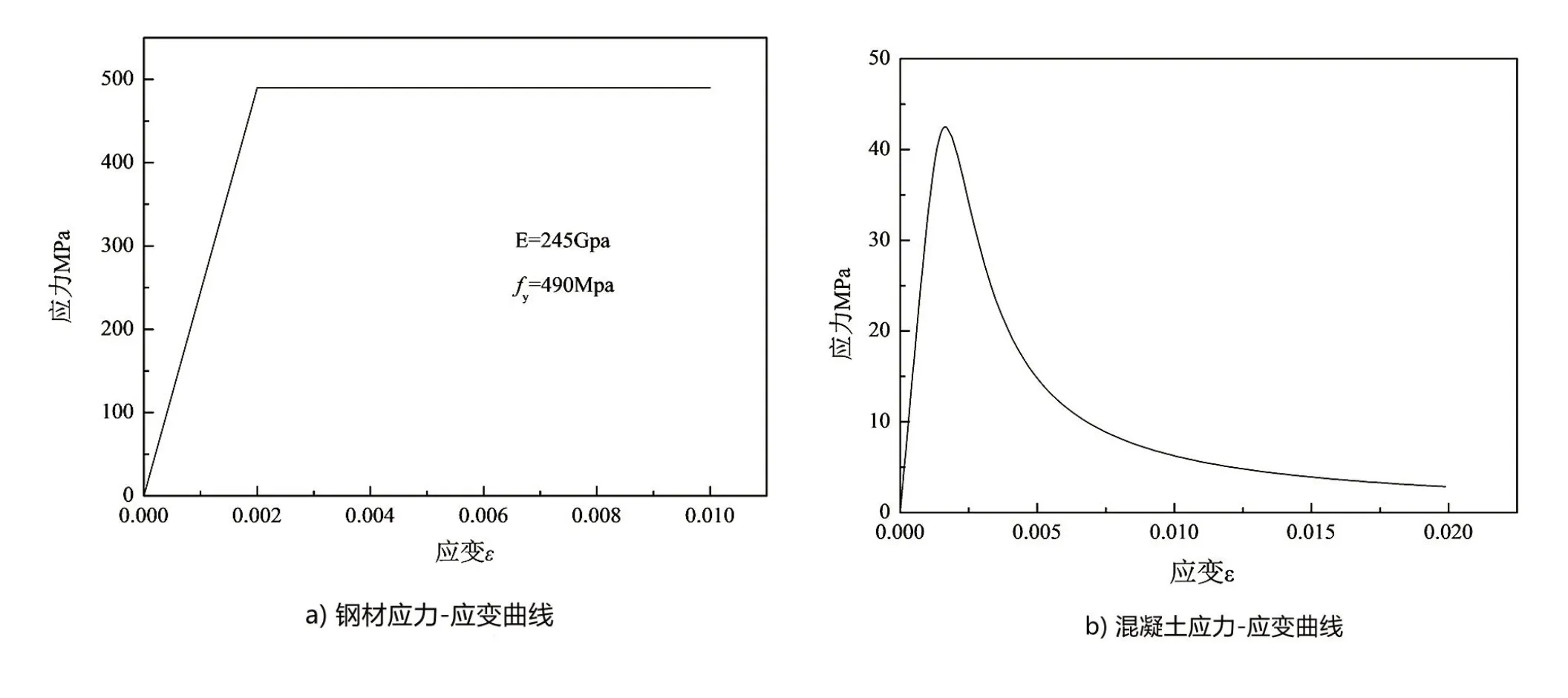
图5 材料本构模型
4.2 单元类型
模型中吊钉和混凝土均采用8节点六面体线性减缩积分的三维实体单元C3D8R。减缩积分单元比完全积分单元在每个方向少用一个积分点。缩减积分的线性单元只在单元中心有一个积分点。
4.3 边界条件和网格划分
根据上述试验结果可知,吊钉发生钢材破坏时,钢材与混凝土之间并滑移量较小,同时由于吊钉底部与混凝土之间作用力很小可忽略不计,因此吊钉底部以上外表面与混凝土之间采用绑定约束。模型中约束混凝土板底部,吊钉与混凝土的网格划分如图6所示。
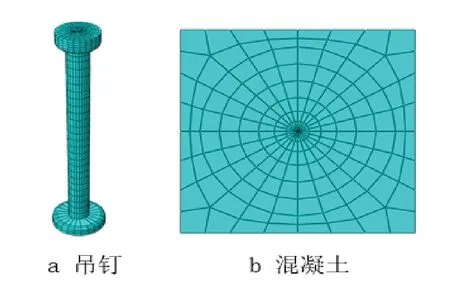
图6 试件网格划分
4.4 有限元计算结果
表4给出了有限元分析的计算结果,并与试验结果及规范计算结果进行了对比,根据表4可知,有限元计算结果大于试验值,主要原因在于钢材极限强度与材性试验值有一定误差。
图7和图8分别给出了在额定荷载、屈服荷载以及极限荷载作用下,吊钉的应力分布情况以及混凝土的塑性应变分布情况。在额定荷载作用下,吊钉的最大应力为283MPa,此时,混凝土在顶部塑性应变较大;随着荷载的增大,当吊钉发生屈服时,混凝土发生塑性变形的深度增大,且混凝土裂缝宽度逐渐增大,当荷载增大至极限荷载时,吊钉顶部变截面处发生明显的径缩,吊钉在一半高度范围内均达到极限强度。
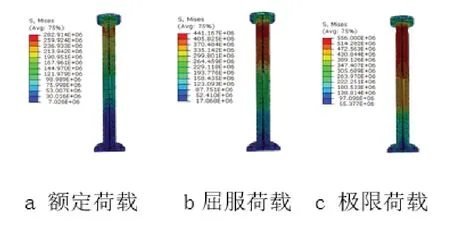
图7 吊钉应力分布情况
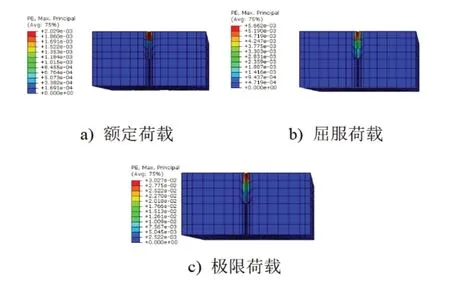
图8 混凝土塑性应变分布
5 结语
①应用ACI318-05规范中的公式与试验结果吻合较好,能够应用于此类吊装配件的设计和分析。
②在轴向拉拔荷载作用下,考虑到混凝土与吊钉的相互作用,计算得到的抗拉承载力与实测值误差较小,说明建立有限元模型具有良好的精度。
③给出了在特征荷载作用下吊钉的内力分布情况以及混凝土塑性变形的分布,对分析荷载作用下吊钉和混凝土的受力情况具有一定的参考意义。
