的高压物性研究

雷慧茹， 张立宏

(山西工程技术学院基础教学部， 阳泉 045000)

1 Introduction

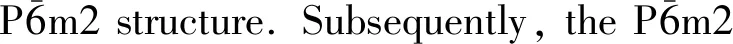
In addition,the elastic constants of a solid are necessary because they are not only closely linked with some fundamental solid-state characteristics, but also correlated with many thermodynamic properties. Most importantly, various mechanical properties are associated with the elastic constants which are indispensable for the practical applications[15]. Hitherto several studies have calculated the elastic constants of ReB3at 0 GPa[13,14], but the elastic constants of ReB3at high pressure have rarely been reported.

The subject of this paper is to investigate the structural, elastic and thermodynamic properties of ReB3under high pressure by using the pseudo-potential plane-wave methods within the density functional theory. In the following, our theoretical methods, results and discussion are presented in detail.

2 Computational detail

2.1 Electronic structure calculations

2.2 Elastic constants

When a material is subjected to an external force within its elastic limit, the elastic constantsCijklunder hydrostatic pressure can be obtained by the coefficients connecting the applied stressσijand the Eulerian strain tensorseklas follows[21,22]:

(1)

whereXandxrepresent the coordinates before and after the deformation, respectively. For an isotropic stress, the specific formulas are[22,23]:

(2)

(3)

wherecijkldenotes the second-order derivative of the infinitesimal Eulerian strain. The strains used are non-volume conserving. Moreover, the number of fourth-rank tensorCis closely related to the symmetry of the crystal. For a hexagonal crystal, the fourth-rank tensorChas five independent componentsC11,C33,C44,C12andC13.

2.3 Thermodynamic properties

The quasi-harmonic Debye model[24]has been successfully investigated the thermodynamic properties of some materials (i.e. TiB2[25], GaN[26]and YbB6[27]). To compute the thermodynamic properties of ReB3, the GIBBS program within the quasi-harmonic Debye model[24]is employed, where the non-equilibrium Gibbs functionG*(V;p,T) can be expressed as:

G*(V;p,T)=E(V)+pV+Avib(Θ(V);T)

(4)

where Θ (V) is the Debye temperature,Avibis the vibrational term which takes the form:

Avib(Θ;T)=

(5)

wherenis the number of atoms in a primitive cell,D(Θ/T) is the Debye integral. The thermal expansion coefficientαcan be obtained from[24]:

(6)

whereγ,BT,CVandCpstand for Grüneisen parameter, isothermal bulk modulus, heat capacity at constant volume, and heat capacity at constant pressure, respectively. The related formulas are[24]:

(7)

(8)

(9)

Cp=CV(1+αγT)

(10)

3 Results and discussion

3.1 Structural features

PhaseResultsa/Åc/ÅV0/Å3B0/GPaP6-m2-ReB3This work2.9214.58233.85313Ref. [14]2.9244.59534.01320Ref. [13]2.9204.59034.01P63/mmc-ReB3This work2.9179.43469.53313Ref. [14]2.9049.31368.04P3-m1-ReB3This work2.8744.66733.40303Ref. [14]2.8744.67333.44

Fig.1 The enthalpy differences for P63/mmc, structure as a function of pressure at 0 K

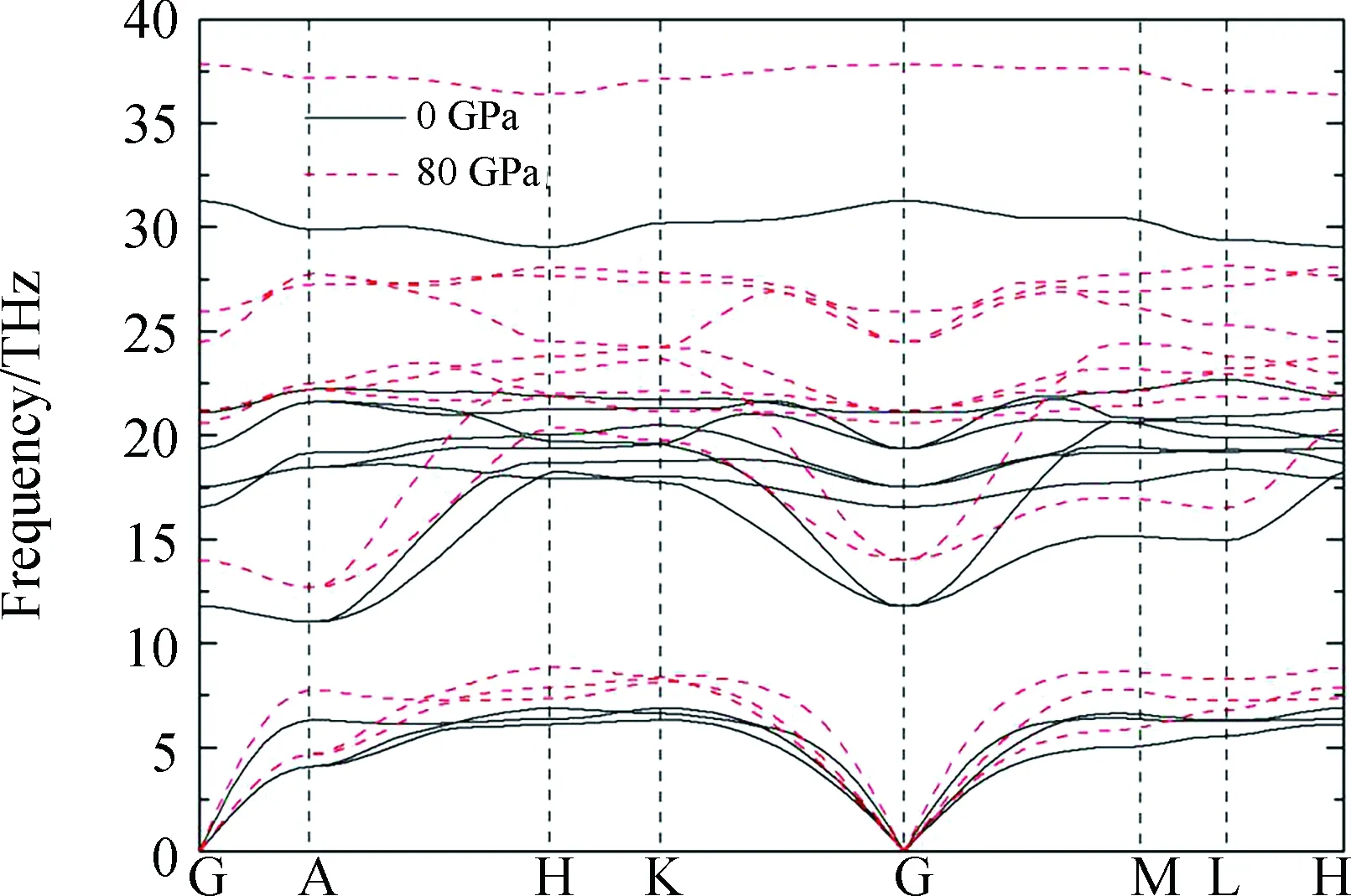
Fig.2 Calculated phonon dispersion relations for the structure

3.2 Elastic properties

(11)

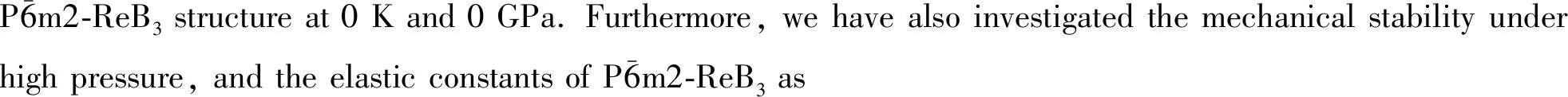
ResultsC11/GPa C33/GPaC44/GPaC12/GPaC13/GPaB/GPaG/GPaB/GE/GPaσΘ/KThis work6009022121041673232401.345770.20773Ref.[14]5679052291301753332391.395790.21764Ref.[13]5759112231401813322351.415700.21

Fig.3 Variations of elastic constants with pressure for the structure

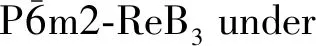
(12)

(13)

(14)

Fig.4 The elastic anisotropic parameters versus pressure for the structure

It is well-known that the hardness can be predicted by the bulk modulusBand the shear modulusG. The Voigt-Reuss-Hill average scheme[32]introduces the methods to calculate the crystal modulus:

(15)

(16)

For a hexagonal structure, theBV,BR,GV,andGRare given as:

(17)

(18)

12C66)

(19)

(20)

where

(21)

The Young’s modulusEand Poisson’s ratioσcan be obtained from the following equations:

(22)

(23)

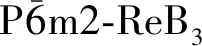
Fig.5 Bulk modulus B, shear modulus G, Young’s modulus E, and Debye temperature Θ as a function of pressure for

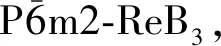
(24)

(25)

whereρis the density. Fig. 6 illustrates all the velocities increase gradually with increasing pressure.

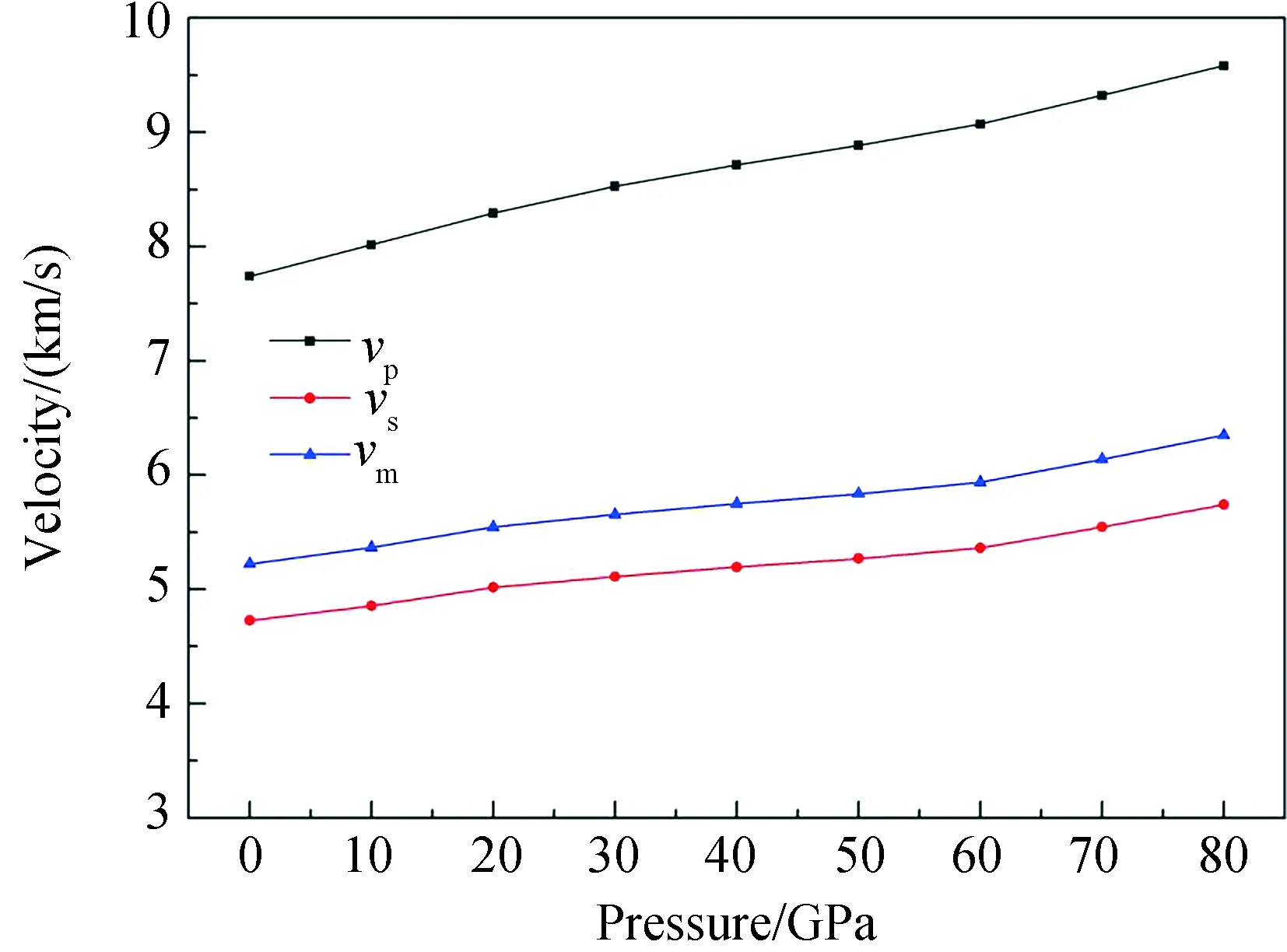
Fig.6 Pressure dependences of aggregate velocities (vp, vs, vm) for the structure

3.3 Thermodynamic properties

It is generally acknowledged that the Debyetemperature Θ is a necessary physical parameter and strongly linked to the elastic constants, melting temperature, thermal expansion coefficient, specific heats, and so on. The Debye temperature Θ can be deduced by using the following formula[35]:

(26)

wherevmis the averaged sound velocity, and can be written as:

(27)

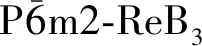
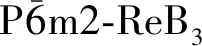
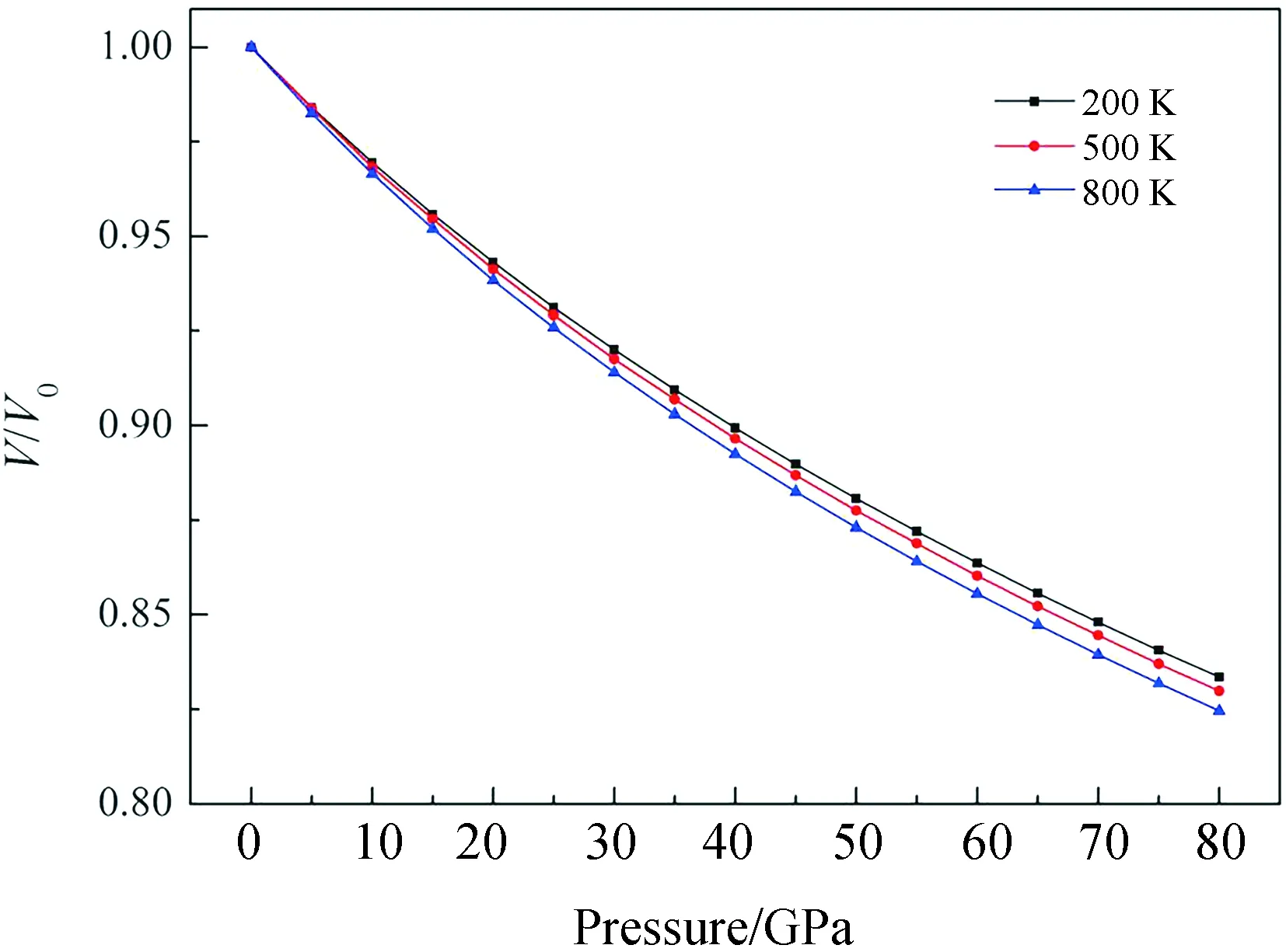
Fig.7 The curves of normalized volume V/V0 vs pressure for the

Fig.8 Dependences of the bulk modulus B on pressure for at 200, 500, and 800 K, respectively

Fig.9 The thermal expansion coefficients α of at various pressures and temperatures

In Fig. 10, we present the variations of the heat capacityCVandCpwith temperatureat different pressures (0, 40, 80 GPa). Clearly, theCpapproaches toCVat low temperatures, but the differences become significantly at high temperatures. TheCVapproaches to a limit while theCpcontinues rising slowly with the increase of temperature. This result can be well elucidated by the Debye model. The anharmonic approximations lead to the sensitivity to temperature and pressure forCVat low temperature. However, the anharmonic effect is suppressed forCVat high temperature, which make theCVapproach to the Dulong-Petit limit. Besides, it can be noted that the effect of temperature on the heat capacity (CVorCp) is greater than that of pressure.

4 Conclusions