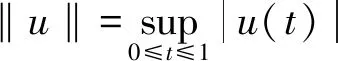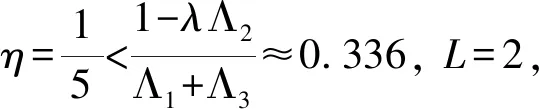一致分数阶微分方程两点边值问题解的存在性
2022-02-10吴玉翠周文学
吴玉翠, 周文学, 豆 静
(兰州交通大学数理学院, 兰州 730070)
1 引 言
分数阶微分方程边值问题是分数阶微分方程理论中的一个重要问题,其绝大部分工作均基于Riemann-Liouville 或Caputo 分数阶导数[1-9]. 2014年, Khalil 等[10]提出了一种与整数阶导数相容的分数阶导数的定义, 即一致分数阶导数.此分数阶导数满足整数阶导数的基本性质, 但与其他分数阶导数之间的关联还未完全明确. 由于其在牛顿力学[11],量子力学[12],任意时间尺度问题[13],混沌系统[14],随机过程[15],扩散迁移[16-18]等领域的应用, 一致分数阶微分方程解的定性性质自然成为应用数学研究的重要课题.
2015年, Batarfi等[19]运用压缩映射原理得到了一致分数阶微分方程三点边值问题
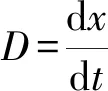
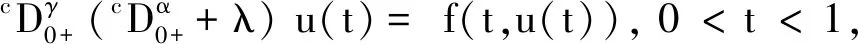
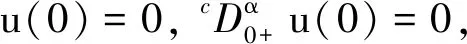
(2)
解的存在性, 其中 0<α≤1, 0<β≤1,Dα,Dβ为一致分数阶导数.
2 预备知识
定义2.1[10]设α∈(0,1], 函数f:[0,∞)→R.则f的α阶一致分数阶导数定义为
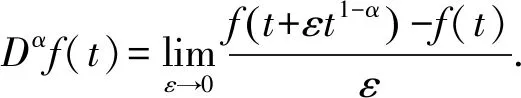
定理2.2[10]设α∈(0,1], 函数f和g在(0,∞)上α次可微.则
(i)Dα(af+bg)=aDα(f)+bDα(g),
∀a,b∈R;
(ii)Dα(tp)=ptp-α, ∀p∈R;
(iii)Dα(λ)=0, ∀λ∈R;
(iv)Dα(fg)=fDα(g)+gDα(f);

定义2.3[21]设α∈(0, 1], 函数f:[0, ∞)→R.则函数f的α阶一致分数阶积分定义为

定理2.4[21]设α∈(0, 1], 函数f:[0, ∞)→R连续.则对任意t∈[0,∞)有
DαIα(f)(t)=f(t).
定理2.5[21]设α∈(0, 1], 函数f:[0, ∞)→R连续且α次可微.则对任意t∈[0,∞)有
IαDα(f)(t)=f(t)+c,
其中c为常数.
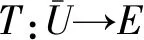

或
(C2) 存在一个u∈∂U和λ∈(0, 1), 使得u=λTu.
引理2.7设h(t)∈C(0, 1)∩L1(0, 1).则一致分数阶微分方程两点边值问题
存在解u(t)满足
(5)
证明 因0<β≤1, 由定理2.5可得
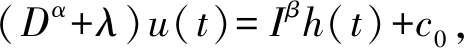
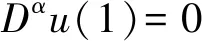
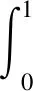
则
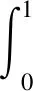
因而
Dαu(t)+λu(t)=
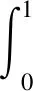
类似地, 由α∈(0, 1]可得
u(t)=IαIβh(t)-λIαu(t)+

其中c1∈R. 利用边值条件u(0)=0可得c1=0.
因此,u(t)满足
u(t)=IαIβh(t)-λIαu(t)+
即
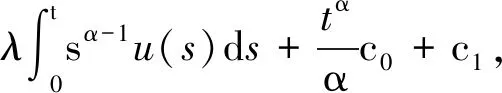
其中
3 主要结果
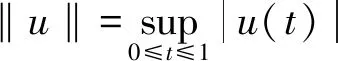
(6)
众所周知,u是边值问题 (3) 式的一个解当且仅当它是算子T的一个不动点.
为了方便, 我们记

定理3.1假设以下条件成立:
(H1)f:[0, 1]×R→R是给定的连续函数,λ为正实数;
(H2) 存在正函数ω(t)∈C[0, 1]和非减函数φ:[0,∞)→[0, ∞), 使得对任意(t,u)∈[0, 1]×R, 有
|f(t,u)|≤ω(t)φ(‖u‖);
(H3) 存在常数M>0, 使得
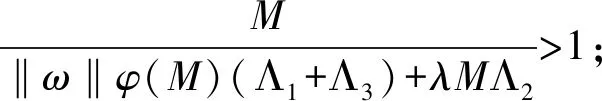
则边值问题(3) 式在[0,1]上至少有一个解.
证明 由算子T的定义和f(t,u(t))的连续性容易证明T是连续的.
首先,T把E中的有界集映为有界集. 对于任意数h>0, 设Bh={u∈E:‖u‖≤h}是E中的有界闭球. 则对任意t∈[0, 1], 有
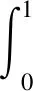
‖ω‖φ(h)(Λ1+Λ3)+λhΛ2.
因此,
‖Tu‖≤‖ω‖φ(h)Λ1+λhΛ2+hΛ3
(7)
下面证明T是等度连续的.对任意的u∈Bh,t1,t2∈[0, 1],t1 |Tu(t2)-Tu(t1)|≤ 即当t1→t2时|Tu(t2)-Tu(t1)|→0.由Arzela-Ascoli定理可知,T是相对紧的, 从而T:E→E是一个全连续算子. 设u是边值问题 (3) 式的一个解.则对t∈[0,1], 类似于前面的方法可得 |u(t)|≤‖ω‖φ(h)Λ1+λhΛ2+hΛ3, 即 下面我们利用Leray-Schauder度理论讨论边值问题 (3) 式的解的存在性. 定理3.2假设条件 (H1) 成立, 并且以下条件也成立: |f(t,u)|≤η‖u‖+L (8) 则边值问题(3) 式在[0,1]上至少有一个解. Br={u∈E:‖u‖ 其中常数半径r>0. 由定理3.1的证明知T是全连续的.则我们可以定义一个连续映射hγ, hγ(u)=u-γTu. 由拓扑度的同伦不变性可知: deg(hγ,Br,θ)=deg(I-γT,Br,θ)= deg(h1,Br,θ)=deg(hθ,Br,θ) = deg(I,Br,θ)=1≠θ, 其中θ∈Br为零元素,I为单位算子. 根据Leray-Schauder度的可解性, 至少存在一个u∈Br, 使得h1(u)=u-Tu=θ.假设存在γ∈[0,1], 对 任意t∈[0,1], 有u=γTu.则 |u(t)|=|γ(Tu)(t)|≤ (η‖u‖+L)(Λ1+Λ3)+λ‖u‖Λ2. 所以 ‖u‖≤(η‖u‖+L)(Λ1+Λ3)+λ‖u‖Λ2. 因此 (9) 由题知 ‖f(t,u(t))‖= η‖u‖+L. 故函数f(t,u)满足条件 (H1) 和 (H4).由定理3.2知边值问题在[0, 1]上至少有一个解.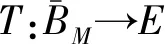
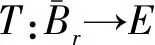
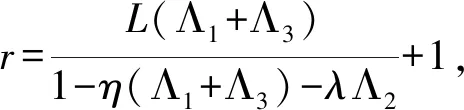
4 例