基于BEMD和QWT的遥感图像去噪算法
2022-02-09成丽波
闫 昊, 成丽波
(长春理工大学 数学与统计学院, 长春 130022)
0 引 言
遥感图像去噪是计算机图像处理领域的关键问题。图像在传输的过程中会受到外界因素的影响,从而影响识别。传统的小波变换可以对遥感图像去噪,其空间域和变换域在遥感图像处理中起着至关重要的作用[1-2]。
1998年,Huang等[3]运用经验模式分解算法(empirical mode decomposition, EMD)进行图像去噪。2003年,法国学者Nunes[4]将EMD扩展为二维经验模式分解算法(bidimensional empirical mode decomposition, BEMD),该方法可以应用于图像压缩、图像融合、图像去噪等方面。2007年,周欣等[5]运用BEMD进行图像去噪,通过BEMD将被污染的图像进行分解,得到一系列细节信息和残余分量信息,并通过实验验证了该方法能有效去除高斯白噪声和乘性噪声。2009年,何培培[6]利用基于BEMD的图像去噪算法进行了图像去噪。
随着对BEMD研究的不断深入,其理论逐渐趋于成熟,研究者们不断改进BEMD方法处理遥感图像。2013年,易三莉等[7]设计了BEMD与自适应维纳滤波的图像去噪算法,该方法将图像分解为不同频率的子图像,分别对每一个子图像去噪。2014年,贺一楠等[8]运用二维经验模式分解方法进行遥感图像去模糊处理。2021年,侯欣雨等[9]提出BEMD二次分解,并与维纳滤波相结合,该方法可以对彩色图形进行去噪处理。
2006年,Corrochano[10]提出了四元数小波变换理论(quaternion wavelet transform, QWT),并用四元数相位的概念推导出四元数小波金字塔。2010年,乔丽红[11]把四元数解析方法运用到提取二维本征模态函数(intrinsic mode function, IMF)的谱特征中,并运用四元数解析方法得到二维解析信号。2012年,Yin等[12]提出四元数小波变换方法,得到去噪图像。同年,殷明等[13]建立了一种基于四元数小波变换的隐马尔可夫树模型,该模型对图像噪声的去除有显著效果。2013年,陈北京等[14]对四元数去除泊松噪声的加权平均滤波器进行深入研究,对彩色图像进行整体处理。2015年,王亚萍[15]详细地介绍了小波变换和双树四元数小波变换理论,并对双树四元数小波变换理论进一步完善,从而达到了图像增强的目的。2017年,Fletcher等[16]对四元数小波变换的内容作了进一步阐述。
本文根据遥感图像信息及噪声分布特征,设计了一种BEMD与四元数小波变换遥感图像去噪算法,通过实验验证该方法具有可行性。
1 二维经验模式分解
EMD方法起初是由Huang等提出,可以处理非线性、非平稳性信号。与传统方法相比,该方法具有显著的优越性。而BEMD是EMD方法的一个推广,它可以将图像f(x,y)分解成若干细节信息和趋势信息,其表达式为
(1)
式中:IMFi表示图像的细节信息,i值越小表示越早分离出来IMF;余项函数r(x,y)表示了图像的结构框架。
2 本文算法实现
四元数域可由实小波和复小波变换推广得到,四元数小波变换相位信息丰富,时频局部化能力较强,它的尺度函数及水平、垂直、对角方向的小波函数的具体形式如下:
(2)
由公式(2)可知,四元数小波变换分为4个实小波,第1个离散的实小波与四元数小波的实部相对应,其余的每个分量分别经过了部分或全部的Hilbert变换。
本文结合BEMD和四元数小波变换算法进行遥感图像去噪,其具体算法如下:
Step 1 将含噪图像进行BEMD分解,得到5个IMF分量和1个残余分量;
Step 2 将第1个IMF分量进行四元数小波变换并对其进行硬阈值去噪,得到的图像进行四元数小波逆变换,最后得到最终的IMF分量;
Step 3 对遥感图像各分量进行重构得到去噪后图像。
3 实例分析
3.1 实验条件
实验采用256×256像素的资源三号多光谱样例图像和高分七号多光谱样例图像作为实验分析对象进行去噪分析,分别添加方差为10,15,20的高斯噪声。
含噪的图像经过BEMD分解得到5个IMF分量和1个残余分量。由于噪声主要存在于第1个IMF分量中,因而需要选取第1个IMF分量;然后对第1个IMF分量进行四元数小波变换并进行硬阈值去噪,再通过四元数小波逆变换得到去噪后的IMF分量;最后通过BEMD逆变换得到去噪后图像,如图1和图2所示。可以看出,该方法能去除含噪遥感图像的噪声,可以突出遥感图像的细节信息。

(a) σ=10(b) σ=15(c) σ=20

(a) σ=10(b) σ=15(c) σ=20
遥感图像去噪质量随着图像方差的增大而降低,这一点从均方误差、峰值信噪比结构相似度可以看出(表1和表2)。

表1 不同方差下资源三号多光谱样例图像去噪质量评价表

表2 不同方差下高分七号多光谱样例图像去噪质量评价表
由图1和图2可知,图像的去噪效果与噪声方差的大小有关,随着方差增大,图像的去噪效果变差,从视觉上看,图像逐渐变得不清晰。由表1和表2可知,图像的均方误差随方差增大而增大,而峰值信噪比和结构相似度随方差增大而减小,实验表明该方法对方差较小的含噪图像去噪效果较好。
3.2 对比实验
本文采用BEMD和四元数小波变换算法完成遥感图像去噪过程并进行了深入分析,与小波算法、BEMD相比,该方法有效可行。
实验采用资源三号多光谱样例图像和高分七号多光谱样例图像作为实验分析对象,但由于条件有限,人为添加了方差为10的高斯噪声,从而得到2幅加噪后的遥感图像。对这2幅图像分别采用BEMD和四元数小波变换算法、小波算法、BEMD进行遥感图像去噪,主观评价如图3和图4所示,客观评价见表3和表4。

(a) 小波去噪(b) 二维经验模式分解(c) 本文方法
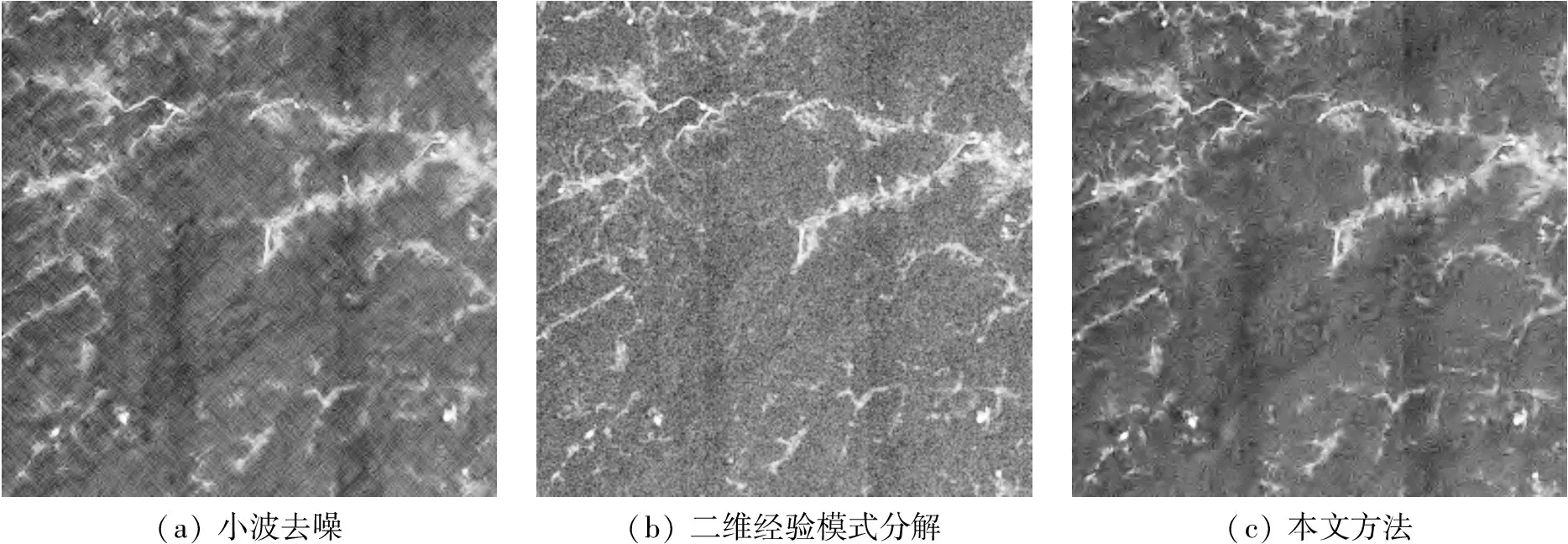
(a) 小波去噪(b) 二维经验模式分解(c) 本文方法

表3 资源三号多光谱样例图像去噪质量评价表

表4 高分七号多光谱样例图像去噪质量评价表
由图3和图4可知,本文方法可以保留遥感图像的细节信息,从视觉上看,该方法具有明显的去噪效果。由表3和表4可知,本文方法可以使图像有较高的峰值信噪比和结构相似度,降低了均方误差,这表明该方法可以弥补传统去噪方法的不足之处,使去噪效果得以提升。
4 结 语
本文将BEMD与四元数小波变换结合进行遥感图像去噪。实验结果表明,本文算法去噪能力优于传统算法,能有效降低图像的均方误差,提高峰值信噪比和结构相似度,从而达到去噪的目的。通过对比实验可以证明该方法确实有效可行,但去噪后的图像仍然不够清晰,图像信息或多或少存在失真的现象。
