基于Hargreaves-Samani 回归修正的作物参考蒸散发计算适用性研究

傅迎豪， 申晓晶， 李王成,2,3， 吴 旭， 张青青

（1.宁夏大学土木与水利工程学院，宁夏 银川 750021；2.旱区现代农业水资源高效利用教育部工程研究中心，宁夏 银川 750021；3.省部共建西北土地退化与生态恢复国家重点实验室，宁夏 银川 750021）

参考蒸散发（ET0）是气候、水文、水资源规划和管理等诸多应用中的一个重要参数［1］，其准确估算对于灌溉系统设计、水资源管理、农业和水文气象研究以及水资源收支的确定至关重要［2-4］。常用的ET0计 算 方 法 有Penman-Monteith（P-M）模 型［5］、Makkink 法［6］、Hargreaves-Samani（H-S）模型［7］。目前，联合国粮农组织1998年提出的P-M模型是较为精确的ET0计算模型［8］。P-M 模型被认为是标准方法，与蒸渗仪在各种气候条件下的实测值和许多其他模式的实测值相比，P-M 模型可以应用于各种环境和气候情景［9］。然而，该模型的计算过程相对复杂，需要用到大量气象数据［10］。包括研究尺度内最高气温、日照时数、最低气温、风速和相对湿度，这限制了它在许多地方的应用，因此需要基于气温等少数气象要素的ET0计算方法。H-S 模型是目前应用最广泛的基于温度的方法之一［11］，基于H-S 模型对ET0的准确估计，可以实现ET0的短期预测。H-S模型虽然简单可靠，但H-S 模型的准确性往往受到当地气象数据的影响，不仅是最高和最低温度，还有风速和湿度［12-14］。研究发现，在不同的气候区域，H-S模型的校正系数每月都有差异［15］。而实际应用中，部分地区观测的气象数据又很难满足P-M 公式的数据要求［16］。因此，结果精确、适用范围广的ET0简化计算方法得以发展。对H-S模型进行修正即可以提高计算精度，对未来的ET0估算也有积极意义。

迄今为止，在全球不同气候条件下，H-S模型的校准和验证已经开展了多项研究。Gavilan 等［17］根据瓜达尔基维尔山谷灌溉区的数据证明，如果使用修正后的方程而不是原来的方程，用水量可以减少11%。因此，为了更好地适应局部区域，有必要对H-S模型进行校准。冯克鹏等［18］通过最小二乘回归对H-S 模型进行修正，确定出宁夏地区每个气象站点的经验系数，从而得出修正后的计算公式。夏兴生等［19］采用线性回归分析方法对H-S模型的系数进行逐月逐区的修正，并以最优选系数确定了不同分区的模型校正系数。这些工作只显示了参数和性能指标值分布的一般规律，缺乏日常评价和大量的站点。为了在高频灌溉中应用更精确的ET0，H-S模型需要使用来自全国众多站点较长的日气象数据序列进行校准和验证。

本研究通过长江中下游平原与西北黄河流域共128个气象站点1961—2020年的逐日数据对H-S模型进行修正，提高该模型对气候因子随时间变化的响应能力。并深入分析比较了该模型在西北干旱半干旱区（西北黄河流域）和湿润区（长江中下游平原）的计算精度与适应性；并对校准后的H-S模型进行未来的适应性分析。

1 研究区概况

长江中下游平原主要由江汉平原、洞庭湖、鄱阳湖、皖苏沿江、里下河及长江三角洲6 块平原组成，地跨湖北、湖南、江苏、江西、浙江、安徽、上海7省市（图1），海拔在5～100 m之间。其大部分位于北半球的亚热带，多年降水量为1000～1500 mm，多年平 均 气 温14～18 ℃，多 年 平 均ET0为1040.91～1091.65 mm。该地区较低的ET0和较多的降雨量使其气候较同纬度内陆地区更为湿润，亦为中国水资源最丰富的地区。该地区降雨量和ET0季节分布较均匀，且与国内大部分湿润区的ET0和降雨空间分布相似。

西北黄河流域的地势西高东低，西部河源地区平均海拔4000 m 以上，地形地貌以高原为主，冰川积雪遍布。其大部分地区年降水量在200～650 mm之间，年平均气温为12～14 ℃。夏季气温高，降水稀少，且自东南向西北逐渐递减。冬季寒冷干燥，水资源相对匮乏，生态环境脆弱。该地区多年平均ET0为845.93～1225.07 mm，较其他半干旱区，该研究区域内流域蒸发能力较强，甘肃、宁夏地区属国内年蒸发量最大的地区，是中亚干旱区的重要组成部分，占国内干旱半干旱区的60%。

2 数据与方法

2.1 数据来源

本研究利用中国气象资料服务中心（http://data.cma.cn）提供的西北黄河流域与长江中下游平原共128 个气象站点1961—2020 年的最高气温、2 m 高处风速、降雨量、日照时数、相对湿度和最低气温等气象资料（站点位置如图1 所示）。对所有站点，分别使用1961—2010年、1981—2010年的数据进行回归修正，2011—2020年的数据进行验证。

图1 气象站点位置示意图Fig.1 Schematic diagram of the location of meteorological stations

降雨是水输入生态系统的主要方式之一，水分条件影响能量成分之间的净辐射分布比例，例如显热通量和潜热通量，从而改变空气水热条件和水气压匮缺，实现对ET0的综合调控［20］。本文根据1961—2020 年128 个气象站点的年均降雨量数据，采用反距离空间插值对研究区域进行降雨量插值，分别对2个研究区范围内的降雨量进行均等分区（图2），以讨论不同水分条件区域ET0计算精度。

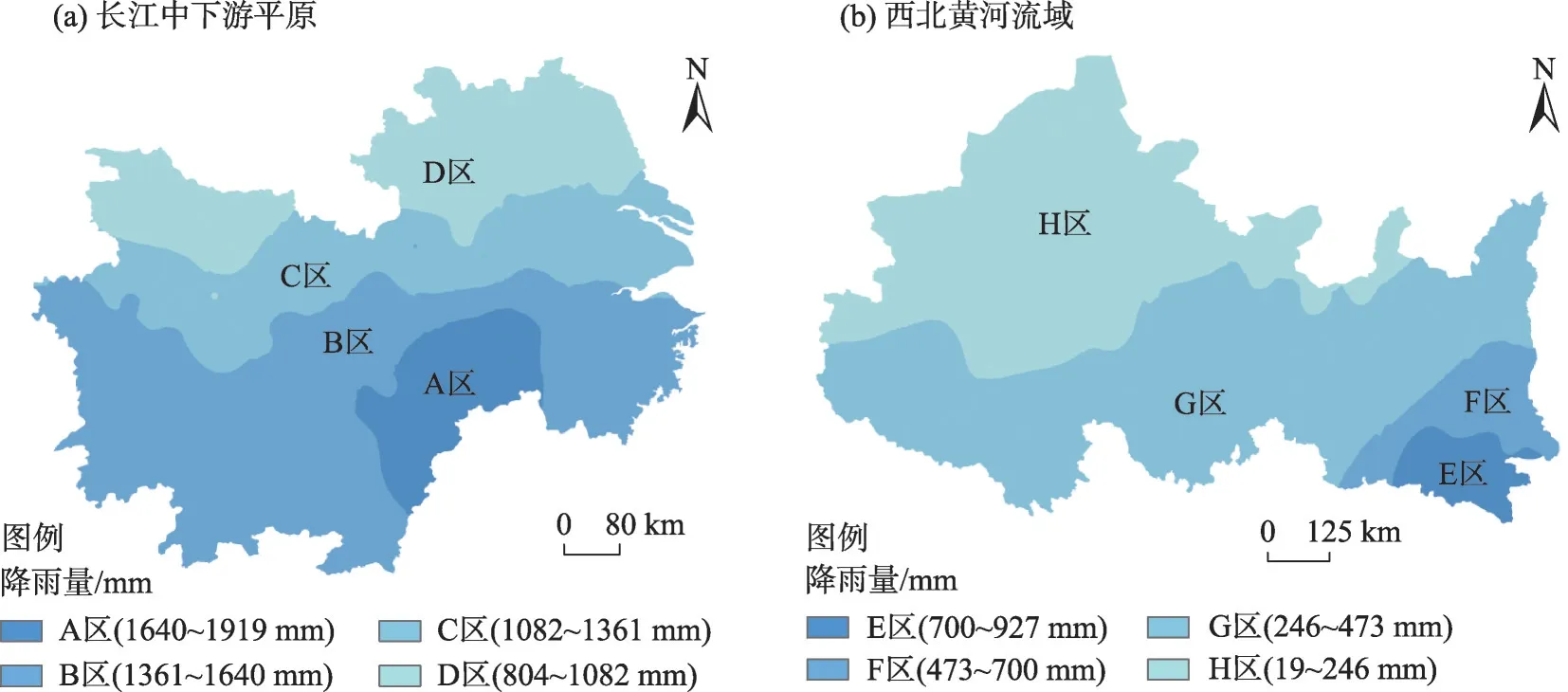
图2 降雨区域划分示意图Fig.2 Schematic diagram of the division of rainfall areas

2.2 H-S模型的校准

2.2.1 参考蒸散发计算方法

（1）P-M模型

P-M 模型［5］被FAO 推荐为计算ET0和评价其他方法的标准方法。因此，将观测气象数据输入模型，利用输出的ET0结果量化H-S模型计算的ET0精度。P-M模型计算ET0（ET0-PM）采用FAO官网推荐的ET0Calculator软件，其计算公式为：

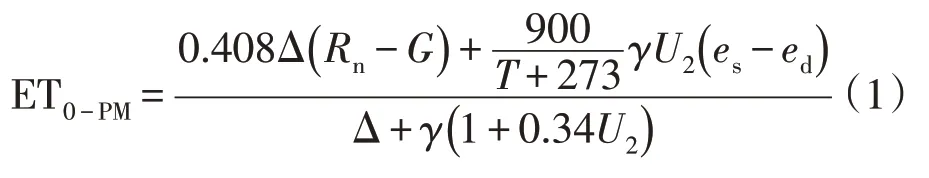
式中：Rn为冠层净辐射（MJ·m2·d-1）；G为土壤热通量（MJ·m2·d-1）；T为平均气温（℃）；γ为湿度计常数（kPa·℃-1）；U2为2 m 高处风速（m·s-1）；es为饱和水汽压（kPa）；ed为实际水汽压（kPa）；Δ 为饱和水汽压与温度曲线斜率（kPa·℃-1）。

（2）H-S模型

H-S 模型是Hargreaves 等［7］在1985 年提出的经验公式，与P-M 模型相比，H-S 模型计算更简单，对气象数据的要求更少，因此该方法可以在世界范围内广泛应用。H-S模型计算ET（0ET0-HS）公式如下：

式中：Ra为天顶辐射（MJ·m2·d-1）；Tmax、Tmin、Tave分别为最高温度、最低温度、平均温度（℃）；Gsc为太阳常数，本文取0.082 MJ·m2·min-1；dr为 日地相对距离（km）；ωs为日落时角（°）；δ为太阳倾角（°），与每天在一年中的序数J有关；ϕ为纬度所转换的弧度（rad）。其中，δ、dr、ϕ、ωs等参数按照下式进行计算：

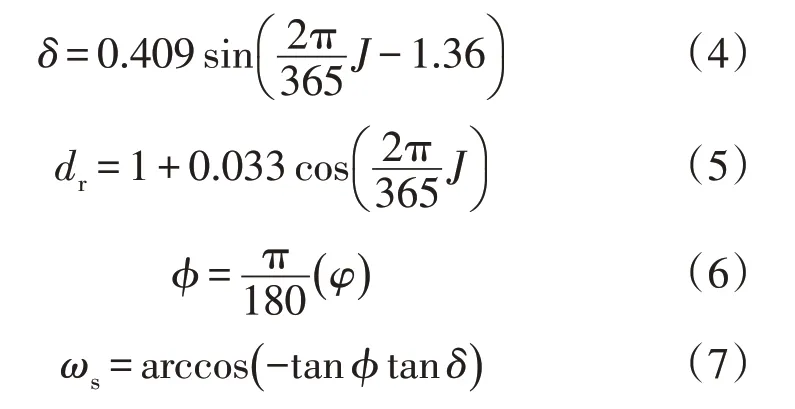
式中：J为一年中的时间序数；φ为当地纬度（°）。

2.2.2 修正方法H-S 模型相比P-M 模型对气象数据的要求更少，且计算过程简单，可以更广泛的运用。但相对于P-M模型，H-S模型对ET0的计算精度较低，因此需要对H-S模型进行修正，以满足精度要求，可以较好的适用于气象数据缺乏的地区。

基于非线性最小二乘方法，提出了对原始H-S模型修正后的H-SCORR模型。研究过程主要包括ET0-PM和ET0-HS的计算（ET0-PM和ET0-HS分别为P-M模型和H-S模型所计算的ET0），H-S模型校正系数的计算以及误差分析，以及对2021—2030 年的ET0预测。本研究选择1961—2010年和1981—2010年2 个校准周期作为校准期，2011—2020 年为验证期。

以各气象站点多年的逐月ET0-PM为因变量，ET0-HS为自变量。建立修正方程ET0-PM=a+bET0-HS，以此计算得出矫正系数a、b，再通过方程ET0-HSCORR=a+bET0-HS结合2011—2020 年的气象资料对H-SCORR模型进行验证（ET0-HSCORR为H-SCORR模型所计算的ET0）。并对比2021—2030 年H-SCORR模型与P-M 模型计算的ET0，对H-SCORR模型进行未来适用性评价，算法改进流程见图3。

图3 算法改进流程图Fig.3 Algorithm improvement flowchart

2.3 精度评估标准

本文以P-M 模型为参考标准，采用平均绝对误差（MAE）、均方根误差（RMSE）、决定系数（R2）3 个指标比较H-SCORR模型与P-M模型计算ET0之间的吻合程度。其中，R2能够反映H-SCORR模型与P-M 模型二者估计值的相关程度，表明两者的变化趋势和分布规律是否一致。MAE 和RMSE 能够反映二者的偏离程度。计算公式如下：

2.4 H-SCORR 模型未来适应性评估

SSP2-4.5 是第五次国际耦合模式比较计划（CMIP5）中RCP4.5情景的更新版本，它结合了一个中等社会脆弱性和中等辐射强迫的情景，该情景还常被用于区域降尺度和年代际气候预测，故选用此场景，与本研究更为契合。以CMIP6气候模拟实验下的ACCESS-CM2 模式，以及未来试验情景SSP2-4.5 对H-SCORR模型进行未来适应性评价。对比2021—2030年H-SCORR模型计算的ET0与P-M模型计算的ET0，进行精度评估。

3 结果与分析

3.1 ET0 空间变化分布规律

从图4可以看出，长江中下游平原的ET0空间分布呈现由南向北递增的趋势，为1041～1092 mm。其中，老河口和房县2 地是ET0的高值中心，为1081～1089 mm，主要由于该地地形等地理环境的影响，对于风速和日照时数的敏感性较高；永州、常宁、道县等地低值中心为1041～1065 mm，主要归因于这3个地区相对湿度较大、日照时间较短。西北黄河流域ET0为846～1225 mm，空间分布从西向东呈现增加的趋势。其中惠农、陶乐、榆林、横山和盐池等地的多年平均ET0最大，为1030.62～1225.07 mm，这些地区日照时间较长，是西北日照时数的高值中心，且相对湿度较小，因此ET0较大。

图4 采用P-M模型计算的ET0空间分布Fig.4 Spatial distribution of the ET0 calculated by P-M model

3.2 H-SCORR 模型精度分析

原始H-S模型、H-SCORR模型和P-M模型计算ET0的统计指标（包括MAE、RMSE、R2）误差分析如图5所示。30 a校准期和50 a校准期分别表现出不同的精度误差，经1981—2010年校准过后的H-SCORR模型精度明显低于1961—2010 年校准模型所计算的精度，说明更长时间序列数据的校准周期可以减少气候变化引起的误差和验证应用存在的误差。长时间序列数据对于模型的修正更加有利，其计算结果更加具有稳定性。因此，H-SCORR模型采用1961—2010年为校准期。

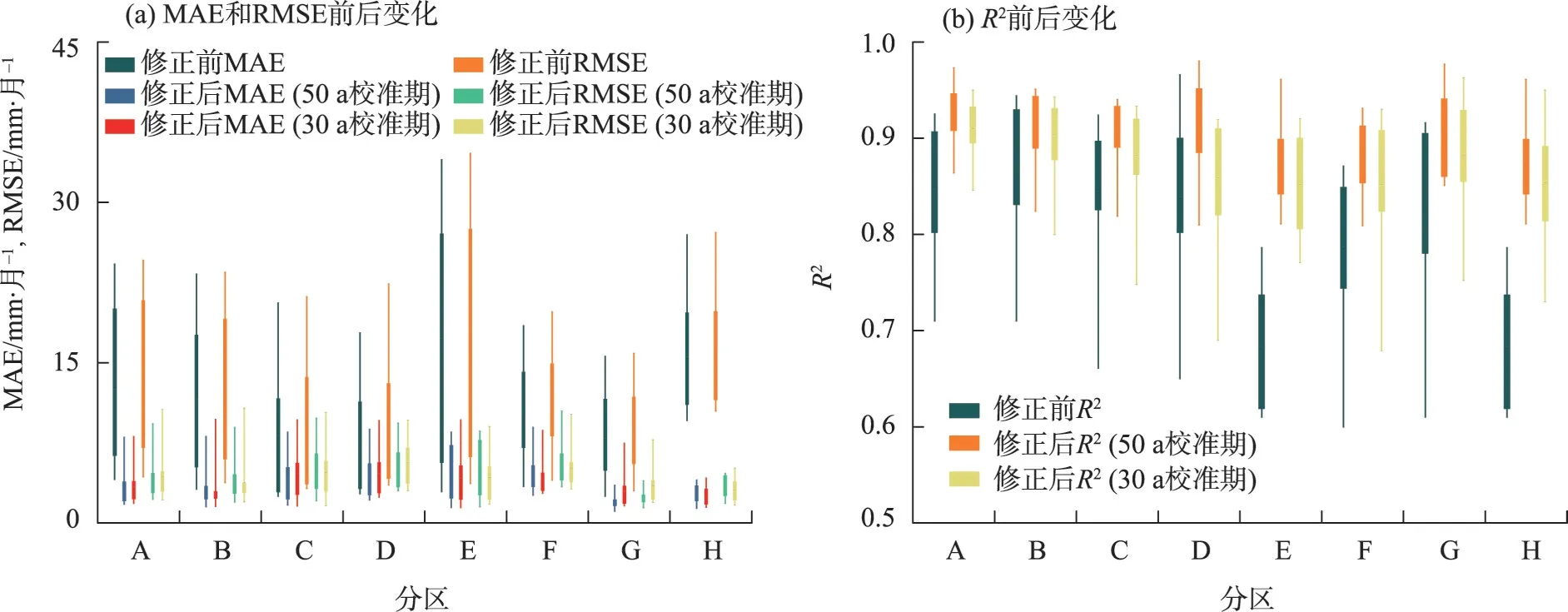
图5 H-S模型改进前后与P-M模型的MAE、RMSE、R²变化Fig.5 Changes of MAE,RMSE and R²between monthly ET0 and the estimated values of the P-M model before and after H-S model improvement

经50 a 校准期修正后的H-SCORR模型其MAE、RMSE、R2在8 个分区都有较好的改善，其相对应的评价精度都有明显的提高。西北黄河流域的4个分区（RMSE=4.18 mm·月-1）整体比长江中下游的4 个分区（RMSE=4.37 mm·月-1）修正效果要好。且修正后的MAE 值下降幅度前者（9.26 mm·月-1）比后者（6.21 mm·月-1）更大，说明H-SCORR模型在西北黄河流域适应性较强。

表1为原始H-S模型和修正后H-SCORR模型的统计指标比较。MAE 和RMSE 的最小值分别最少降低了0.60 mm·月-1和0.56 mm·月-1，最大MAE 和RMSE分别至少减少了9.00 mm·月-1和9.28 mm·月-1，MAE 和RMSE 平均值分别下降了7.73 mm·月-1和7.81 mm·月-1，修正后R2值大部月份均大于0.9，R2最少提高1%。这些结果表明，用修正后的参数计算出的ET0值更为准确，说明修正后H-SCORR模型可用于该研究区域ET0的估算。对于西北黄河流域，经修正后，大部分地区的MAE在1.11～8.94 mm·月-1之间。对于长江中下游平原，H-SCORR模型的精度比西北黄河流域略低，修正后的效果略不足，H-SCORR模型在西北黄河流域的精度较高。总体而言，H-SCORR模型在研究区域内的表现均明显强于原始H-S模型。

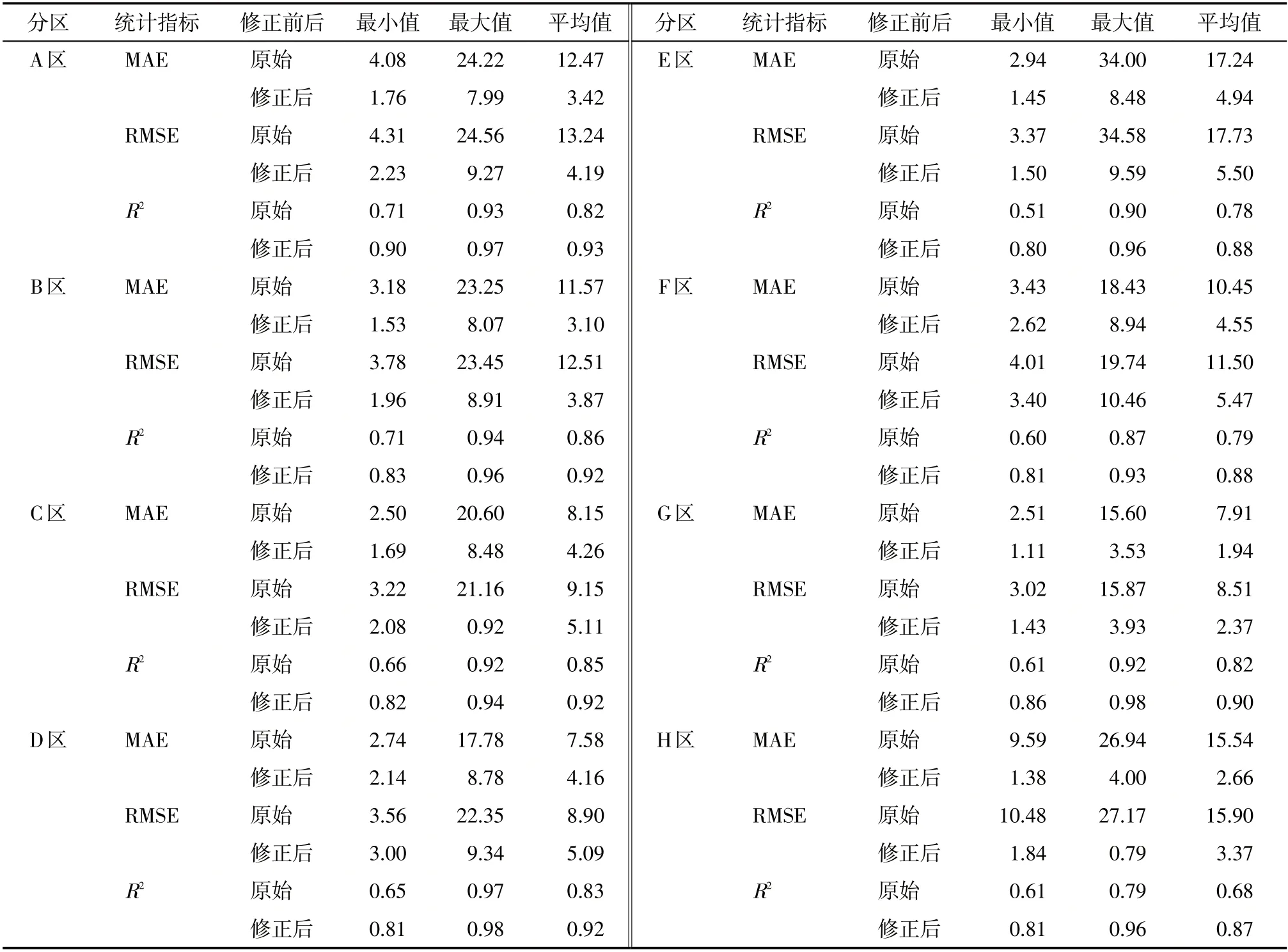
表1 原始H-S模型和修正后H-SCORR模型的统计指标对比Tab.1 Comparison of statistical indicators between the original H-S model and the revised H-SCORR model

3.3 H-SCORR模型的应用

因H-SCORR模型在西北黄河流域的适应性较强，故选取在西北黄河流域的E区来进行H-SCORR模型对于2021—2030 年的ET0模拟，以此来验证H-SCORR模型在未来的适用性。基于CMIP6 模式数据评估了H-SCORR模型在未来的模拟能力，并给出了未来ET0的变化。本文选取了CMIP6气候模拟实验下的ACCESS-CM2 模式，以及未来试验场景SSP2-4.5。在对2021—2030年的ET0模拟中R2均达到了0.98以上。图6、图7表明H-SCORR模型对ET0的季节循环以及长期变化趋势均有较好的模拟能力。因此，HSCORR模型在未来也同样具有一定的适用性。

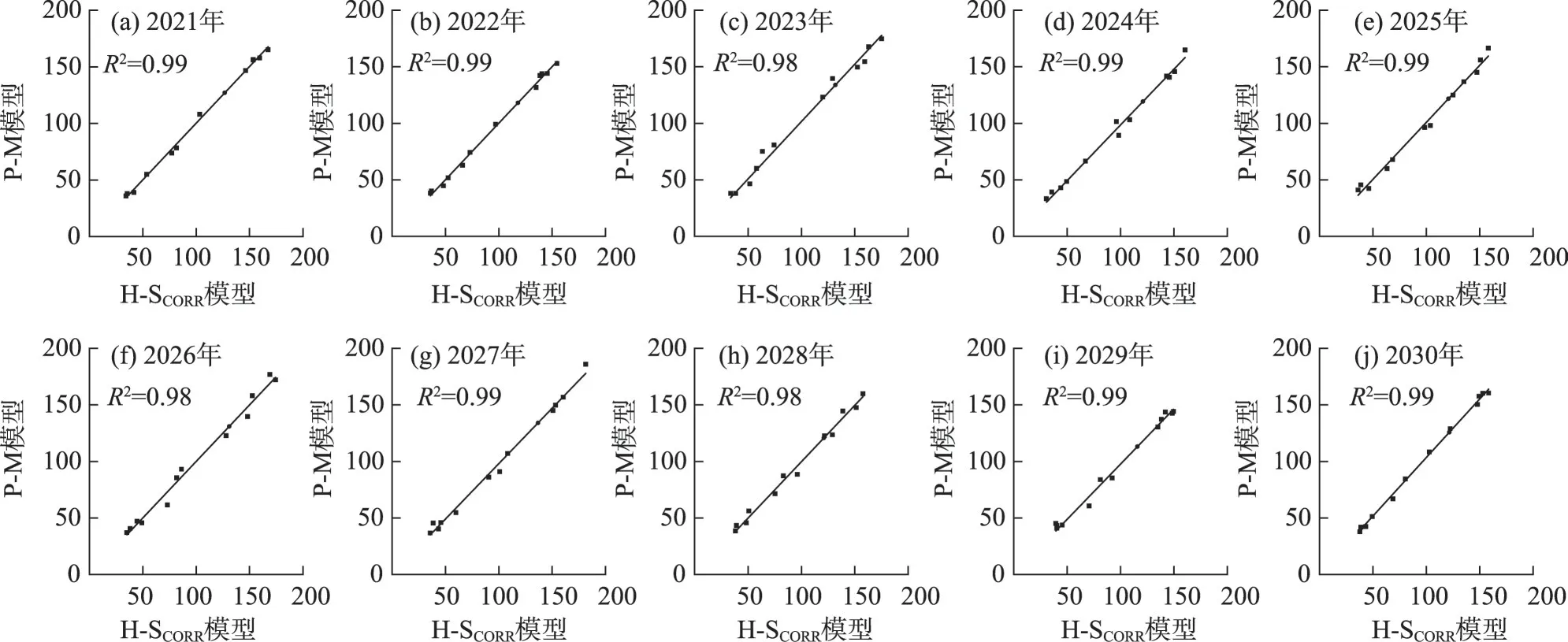
图6 ACCESS-CM2模式下2021—2030年ET0逐月值与H-SCORR模型计算结果拟合Fig.6 Fitting of monthly ET0 values from 2021 to 2030 under ACCESS-CM2 mode and the calculation results of the H-SCORR model

图7 ACCESS-CM2模式下2021—2030年ET0逐月值与H-SCORR模型计算结果对比Fig.7 Comparison of monthly ET0 values from 2021 to 2030 under ACCESS-CM2 model and the calculation results of the H-SCORR model

4 讨论

ET0的准确估算对于水资源管理、农业和水文气象研究以及水资源收支的确定至关重要［21］。本研究通过2 个研究区域的128 个气象站点1961—2020 年的逐日数据对H-S 模型进行修正，并进行未来的适应性分析。

然而，尽管H-SCORR模型在该研究区域的精度有所提高，但对个别精度较差的区域仍需要进一步改进。且H-SCORR模型存在明显的空间变异性，不同研究区域的时间和空间尺度存在差异。本研究的时空尺度较大，地理环境复杂，所以在未来的研究中不仅要考虑不同时间尺度下的校正精度，还需要对不同小区域尺度的校正系数进行进一步的研究。本研究利用校正系数消除了风速、降雨和湿度等气候因子对于区域ET0的影响，但在实际应用中，这种方法无法直观地反映气象因子与H-SCORR模型的直接关系，气候因子对ET0估算的影响还需进一步的讨论，因此H-SCORR模型不是为了取代P-M 模型，而是在只有气温数据的情况下可以更加有效地估算ET0。

5 结论

（1）经修正后，H-SCORR模型具有较高的精度，其估算的ET0值更接近于P-M模型。长江中下游平原MAE和RMSE的平均值分别下降了6.21 mm·月-1和6.38 mm·月-1。西北黄河流域MAE和RMSE的平均值分别下降了9.26 mm·月-1和9.23 mm·月-1，2 个研究区域的大部分月份的R2均大于0.9，少数月份的R2大于0.8，校验后的R2比校正前最少提高1%。H-S模型经校正后计算精度和适用性得到了进一步提升。

（2）在ACCESS-CM2 模式中，H-SCORR模型在未来气候条件下依然具有很强的适用性。因此，HSCORR模型可用于研究区域的蒸散发预报，有助于进一步研究蒸散发预报。

（3）在长江中下游平原和西北黄河流域的具体验证应用中，其绝对误差结果表现参差不齐，但整体的绝对误差都显著缩小，在西北黄河流域的验证中效果优于长江中下游平原，因此H-SCORR模型在西北黄河流域具有更佳的效果。