融合聚类算法的改进麻雀搜索算法
2022-02-09欧阳城添朱东林邱亚娴
欧阳城添,朱东林,邱亚娴
(江西理工大学,江西 赣州 341000)
1 引言
近年来,随着各种优化问题被提出,对应着优化算法被逐渐开采,意在解决各种工程复杂问题。麻雀搜索算法是在2020年提出来的新型群智能优化算法。该算法受麻雀觅食等行为启发,在优化问题上较粒子群(Particle Swarm Optimization,PSO)、灰狼算法(Grey Wolf Algorithm,GWO)、遗传算法(Genetic Algorithm,GA)等传统的智能优化算法有着明显的优势。但其同样存在陷入局部最优的概率且寻优结果具有较大的随机性。
对此,许多学者针对麻雀搜索算法的缺陷提出不同的方案改进,并成功地应用在工程问题上。吕鑫[2]等学者提出一种混沌麻雀搜索算法(CSSA),首先采用基于随机变量的tent映射初始化种群,使得种群分布均匀,再使用混沌扰动及高斯变异防止算法在寻优过程中出现麻雀个体局部聚集,出现陷入局部最优的现象;最后将改进的算法应用于图像分割,并取得了良好的效果;毛清华[3]等学者提出了一种融合柯西变异和反向学习的麻雀搜索算法,采用sin混沌初始化种群,再在发现者位置更新公式中移入上一代的全局最优解,同时也引入了自适应权重策略,平衡了局部与全局搜索能力,最后在最优解位置融合柯西变异与反向学习策略,增强算法跳出局部最优的能力,在8个标准测试函数上验证了此算法的有效性。汤安迪[4]等学者提出了一种基于混沌麻雀搜索算法的航迹规划方法。首先,该算法采用立方映射初始化种群,并使用反向学习策略保证了种群的均匀性。再采用精英反向学习策略扩大精英反向解的搜索区域,在追随者位置更新上引入正余弦算法,增加了种群多样性,最后对警戒线数量进行线性衰减,平衡了算法全局性与局部性搜索。通过15个标准测试函数证明了该算法的优越性,同时在有威胁的情况下进行路径规划仿真,与其它优化算法相比,验证了该算法的实用性。这些改进的算法均有一定的成效,但初始化种群方法依然存有一定的随机性,不能保证每次迭代之后的分布都是均匀的,在寻优过程中采用的策略具有区域局限性,未能在整个空间内进行全局搜索,这样依然存在陷入局部最优的概率。
在总结前人的工作上,本文提出融合聚类算法的改进麻雀搜索算法(KDLSSA),起初利用K-medoids动态更新种群个体位置,保证了种群的均匀性与多样性,再引入基于重心的反向学习策略,弥补了一般学习策略没有充分利用种群空间的情况,使发现者具有广阔的搜索范围且防止过早的收敛,最后在追随者引入自适应余弦权重策略保证了算法具有细致且灵活的搜索能力,平衡了算法全局性与局部性搜索。在8个测试函数上验证了改进算法的有效性及实用性。
2 麻雀搜索算法
在麻雀觅食的过程中,分发现者和追随者两个行为策略。发现者一般为种群数量的0.2,是种群个体的引导者,它带领着其它个体进行食物的寻找,因此发现者具有广阔的搜索范围。发现者的位置更新公式如下

(1)
式(1),h表示当前的迭代次数,M为最大的迭代次数。Xi,j表示当前第i个麻雀在第j维中的位置。α∈[0,1],且是一个随机数。R2和ST分别代表预警值和安全值,且R2∈[0,1]、ST∈[0.5,1]。Q是一个正态分布的随机数。L表示一个元素全为1的1×d的矩阵。当R2 追随者为了获取优质食物,紧随发现者之后,其中部分追随者会监督发现者及和捕食率较高的发现者争夺食物,从而提高自身的营养。 追随者的位置更新描述如下 (2) 式(2)中,Xp是发现者当前所占据的最优位置,Xworst表示当前的最坏位置。A为一个元素仅是1或-1的1×d的矩阵,其中A+=AT(AAT)-1。当i>n/2时,这时当意识到危险时,麻雀种群会做出反捕食行为,其数学表达式如下 (3) 式(3)中,Xbest是当前的全局最优位置。β为控制步长参数,是服从均值为0且方差为1的正态分布的随机数。K∈[-1,1]是一个随机数,fi表示当前麻雀个体的适应度值。fg和fw分别当前搜索范围内最优及最劣适应度值。ε为最小的实数,防止分母出现0的情况。当fi≠fg表示当前的麻雀处在种群的边界,容易受捕食者的攻击,需要调整位置。fi=fg时,这表明处于种群内部的麻雀个体意识到了危险,为躲避危险,需要靠近其它麻雀的位置,K代表麻雀移动的方向同时也可以控制移动步长。 麻雀搜索算法寻优能力较好,但每次寻优结果存在较大的随机性,依赖于初始化种群的麻雀个体的位置,因此每次得到最优解的稳定性较差。本文采用经典聚类算法K-medoids对种群进行动态分割,将麻雀个体进行分类聚化,在初期阶段进行个体分类,减小初期工作的复杂性,加快了信息交流,之后随着迭代次数变化而变化,提高了种群的多样性,在一定程度上减小了陷入局部最优的概率。 K-medoids算法是目前运用范围较广的聚类方法,具有对数据敏感性强且鲁棒性好等优点。与K-means算法相似,两种算法的差异在于聚类中心数的选取,K-means算法是将当前簇中所有个体的平均值作为聚类中心点,但这点存在不可靠性,若该点不是当前最优点附近会有误导性,反而增加了无用功,K-medoids算法是直接选取当前簇中的一个个体作为聚类中心点,且要满足簇中其它所有点到这个个体的距离最短,这样使得聚类中心点具有代表性。具体K-medoids聚类过程如下: Step1:从麻雀种群中随机选择K个个体作为初始聚类中心点。 Step2:计算其它个体到各个聚类中心的距离,根据距离最小原则,将各麻雀个体划分到最近的簇内。 Step3:计算每个簇内所有个体的均值,根据距离最小原则,选取离均值点最近的个体作为聚类中心。 Step4:不断重复step2,直到最大迭代次数进行终止。 发现者在整个寻优过程中起着引领作用,因此发现者必须有着广阔且灵活的飞行方式,它的寻优质量直接影响着算法的收敛速度与最优解的质量。在麻雀搜索算法中,发现者有其自身的飞行方式,但在寻优效率及质量上难以保障,一旦陷入局部极值状态就会限制算法的整体性能。反向学习是评估当前解与反向解加速搜索进程的一种技术。一般的反向学习策略在智能优化算法上取得了较好的效果,但一般的学习策略仅仅在部分空间上进行反向搜索,针对此问题,本文引入基于重心的反向学习策略,弥补了其没有充分利用整个种群空间的能力,使算法在整个空间内动态变化,加快了个体搜索效率,能够全面探索整个空间,维持种群多样性,极大地提升了算法的寻优能力。 定义1重心:设(X1,X2,…,Xn)是D维空间中带有质量的n个点,那么整体的重心为 (4) 定义2重心方向点:若一个离散均匀的整体的重心为M,则M中某一点Xi的反向点为 (5) 反向点存在于一个具有动态边界的搜索空间,记为Xi,j∈[aj,bj]动态边界的表达式为 aj=min(xi,j),bj=max(xi,j) (6) 若反向点超出规定边界时,需按式(7)重新计算反向点 (7) 采用基于重心的反向学习策略拓宽了麻雀个体飞行的区域,提高了种群的工作效率,在复杂函数寻优时具有良好的突变性,摆脱局部极值的吸引。 追溯者紧跟发现者寻找优质解,这样导致其具有盲目性且丧失独立性,智能优化算法循规蹈矩的寻优存在一定局限性,因此采用动态调节的方法进行灵活寻优,本文在追随者位置更新阶段引入自适应余弦权重策略,动态调节当前当前个体对下一代个体寻优的影响,从而提升了追随者的寻优手段。引入自适应余弦权重的追随者更新公式如下 (8) (9) (10) 上述式中,wmax与wmin分别为最大权重与最小权重;Sstop为停止阈值,本文为常数0.001,用来减小算法在迭代中重复计算w的频度。 引入自适应余弦函数惯性权重,使得追随者搜索随着迭代次数而变化,余弦函数提高了追随者阶段的灵活性,搜索变得更加细致,同时在中期防止陷入局部最优,后期增大了收敛精度。 本文提出的融合聚类算法的改进麻雀搜索算法,首先采用K-medoids初始化种群,动态分布每个麻雀个体的位置,提高了算法的种群多样性,再引入基于重心的反向学习策略,使得发现者的位置搜索具有广阔性,充分利用到了整个给定空间,在一定程度上防止了算法陷入局部最优,再提出了一种自适应余弦惯性权重,使得追随者个体具有灵活性,改善了其具有盲目性的缺陷,前期增大了算法的收敛速度,后期提高了其搜连精度。多种策略的引入使得算法在寻优能力上具有较好的灵活性,平衡了算法全局性搜索能力与局部性搜索,找到可靠解。具体算法流程如下: 1)初始化参数。设置种群规模、迭代次数及初始聚类中心数K。 2)根据聚类算法K更新化麻雀个体的位置。 3)计算适应度函数。得出最小及最大适应度值。 4)从部分麻雀个体中选择发现者,并按式(5)~(7)更新发现者的为位置。 5) 根据式(8)更新追随者的位置。 6)根据式(3)更新意思到危险的麻雀位置。 7)判断是否达到迭代次数,是则进行下一步,否则跳转步骤2) 8)算法结束,输出最优值及对应位置。 本文选取个标准测试函数对改进的麻雀搜索算法进行对比实验,将PSO,GWO,SSA,CSSA,KSSA算法加入本实验进行试验对照,CSSA算法式来自文献[5],KSSA算法采用K-means动态更新种群,且其它策略与KDLSSA算法不变,种群数量为50,迭代次数为200,K设定为5。在SSA及其变体中,发现者及侦察者的比例均为0.2,其它算法的通用参数保持一致,标准测试函数如表1,采用8个不同类型函数来验证改进算法的可行性,前四个函数为单峰函数,中间三个函数为复杂多峰函数,最后一个为易陷入局部最优的固定维度函数。为了使实验效果更具说服力,将各算法独立运行30次,统计各自的最优值、平均值及标准差。三个指标用来衡量各算法的稳定性及寻优能力。各算法运行结果如表2。 表1 测试函数表 表2 各算法性能测试表 从表2来看,KDSSA较其它优化算法具有显著的寻优能力。在单峰函数上,KDLSSA存在较好的收敛精度,特别在F1与F3函数中,KDLSSA算法可以直接找到最优值,在多峰函数上,KDLSSA存有较好的抗局部极值吸引能力,在寻优效果上有着明显的改善,在F5与F6函数中,KSSA也同样有着较好的收敛能力,但其稳定性较差,在F8函数上中,各算法都能找到最优值,但各算法稳定性较差,KDLSSA的标准差值最小,具有较高的稳定性。综上所述,多种策略的引入使得算法在寻优效率上有者明显的提升,且摆脱了原算法寻优机制的束缚,找到质量更高的解。 为了更好地描述各算法在各函数中的寻优轨迹,画出各算法的平均收敛曲线如图1所示。 图1 各算法平均收敛曲线 如图1内容可看出,KDLSSA算法具有较好的收敛效果,在F1-F3及F6函数中,KDLSSA与KSSA的收敛精度差异不大,但KDLSSA收敛速度较快,在其它函数中,KDLSSA与其它改进的麻雀搜索算法的寻优差异不大,但有较快的收敛效果。综上所述,K-medoids聚类算法的引入较K-means算法具有较好的寻优推动能力,在基于重心的反向学习策略与自适应余弦权重的引入下,使得算法在广阔的空间内执行广泛而细致的搜索,提高了算法的收敛能力,同时也在寻优效率上得到显著的提升。 在目前众多改进的麻雀搜索算法依然存在陷入局部最优且收敛速度较慢的基础上,本文提出融合聚类算法的改进麻雀搜索算法,该算法初期采用K-medoids聚类算法对麻雀种群进行动态更新,防止过早收敛且加快了初期寻优效率,其次在发现者阶段引入基于重心的反向学习策略,摆脱了一般反向学习策略仅在有限的空间内进行搜索的弊端,提高了算法的全局性搜索,最后在追随者阶段引入自适应余弦权重策略,使得追随者摆脱自身的盲目性搜索,且搜索变得广泛而细致,平衡了局部与全局性搜索。通过8个不同类型的标准测试函数,证明了改进的麻雀搜索算法KDLSSA比其它算法的优化能力更佳,在寻优效率上也更胜一筹。但在高维复杂情况下,KDLSSA算法仅在收敛速度上比较显著,而收敛精度上没有得到显著的提升。在后期,如何使得算法在复杂函数下平衡收敛速度与收敛精度是往后研究的重点。

3 改进的麻雀搜索算法
3.1 K-medoids聚类算法
3.2 基于重心的反向学习策略


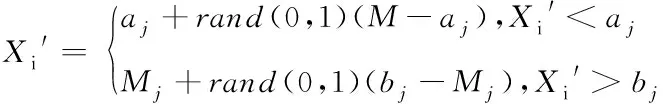
3.3 自适应余弦惯性权重



3.4 改进的麻雀搜索算法流程
4 实验结果与分析
4.1 参数及环境设置

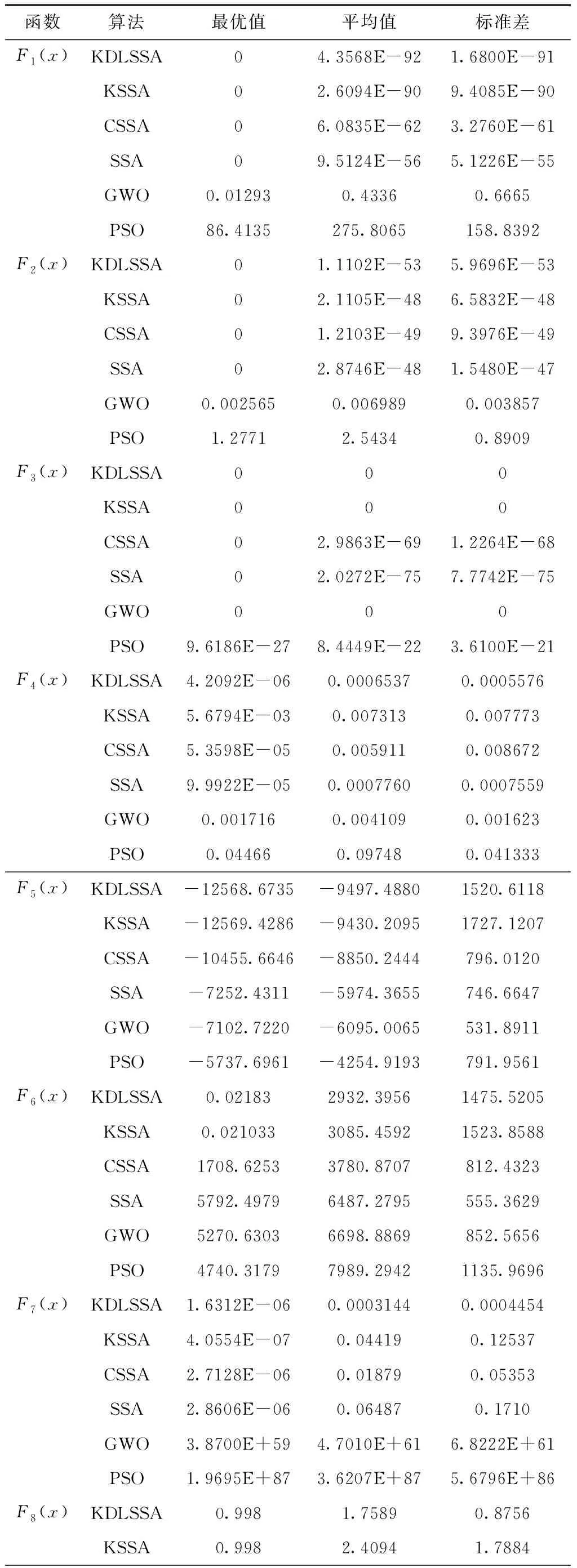
4.2 收敛性分析

5 结束语
