基于PSO-GA算法的交叉口仿真优化研究

任永泰，邓 朝，王紫阳

(1. 东北农业大学文理学院，黑龙江哈尔滨 150030；2. 东北农业大学工程学院，黑龙江哈尔滨 150030)

1 引言

随着城市的快速发展，交通拥堵已成为城市中的严峻问题，直接影响是延误增加，造成交通运行效率的降低[1]。而交叉口发生拥堵的主要原因是信号周期的不合理分配[2]。因此，为了缓解交通拥堵、提高运输效率，交通信号的控制和优化至关重要[3]。

针对交通信号配时及交通拥堵的问题，研究人员提出将自然启发算法用于交通系统的控制和优化[4-5]，根据该算法的更新技术，可分为两种。第一种是进化算法(EA)[6]，作为EA的代表算法，遗传算法(GA)广泛运用于交通灯信号优化配时中[7]。Kou[8]使用GA找到了最佳信号配时，提出的GA优化模型取得了更好的效果。高云峰[9]以非饱和交叉口作为实验对象搭建了定周期信号控制的多目标优化模型，并运用非支配排序遗传算法求解。但是GA的局部搜索能力较差，后期搜索效率较低，整个迭代过程也比较费时。第二种是群智能(SI)算法，作为SI算法之一，PSO所具有的全局最优引导能力引起了研究人员的广泛关注[10]。Dabiri[11]使用PSO优化了动脉交通信号的时序参数。与信号优化工具Vistaro的时序计划相比，PSO生成的时序方案使时间延迟大幅降低。但是，PSO可能使问题陷入局部最优。因此，结合两种自然启发算法的优缺点，本文提出了一种遗传算法-粒子群优化算法(PSO-GA)，并将其用于交通信号配时的模型求解中。

PSO-GA算法是PSO的改进算法，利用了PSO的全局引导能力并引入GA的交叉和变异算子，具有收敛速度快和强鲁棒性的特点，能找到目标函数的全局最优解。PSO-GA可用于函数优化并应用于许多问题，如利用PSO-GA优化神经网络，TSP问题，资源分配问题[12-13]。但就目前而言，很少有学者将PSO-GA运用于交通信号时序优化。

此外，Synchro[14]软件作为一种典型的交通微观仿真软件，被广泛应用于交通流模拟和优化。灵敏度分析也是检验不同变量对目标影响的有效工具[15]。综上，本文提出使用PSO-GA求解交通时序优化问题，用Synchro软件进行交通仿真并使用灵敏度分析讨论了车流量对交通运行的影响。

与现有研究相比，本文的研究有以下贡献：①将PSO-GA运用于交通信号时序优化中，通过与其它方法对比验证了算法的有效性。②将交通信号时序优化技术与交通模拟工具相结合，开发了一种基于模拟优化的模型。③进一步讨论了高低车流量变化对交叉口运行效率的影响，为相关交通运输部门提供理论支持和实践指导。

2 建立信号控制多目标优化模型

为提高交通运行效率，本文研究了交叉口信号周期的优化调整策略，以周期时长和饱和度作为配时参数，将车辆延误、停车次数和交叉口通行容量作为路口信号配时优化的三个重要指标，建立了多目标优化模型，以优化现有时序方案。

2.1 车辆延误

常用的时延是基于Webster模型的。但是，在低饱和度条件下Webster模型才比较适合。因此，本文对Webster模型进行了改进，将延误定义为

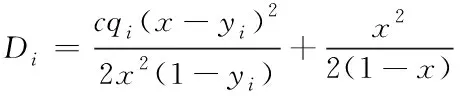
(1)

2.2 平均停车次数

停车次数即一个周期信号中完全停车次数的总和，它的增加会带来延误的增加，与饱和度成反比，交叉口第i相位的平均停车次数可定义为

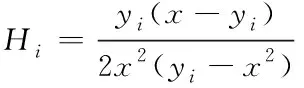
(2)

2.3 交通容量

相位交通容量即指相位通行能力，它是指相位关键车道的通行能力，定义如下

(3)

这里Si是指相位i的饱和流量。

2.4 多目标优化模型的构建

考虑实际状况，将交叉口信号配时优化的三个目标采用加权方式转化为单目标求解问题。这样简化后的目标函数表示为

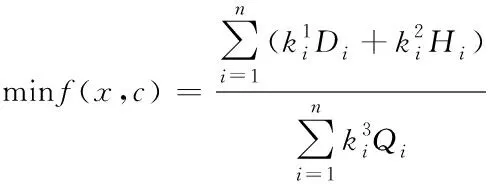
(4)

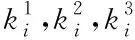
(5)

3 算法设计与模型仿真

3.1 混合PSO-GA算法的简介

PSO算法可以记住全局最优状态和个体最优状态来影响粒子的运动模式，而这种全局最优导引能力可以导致快速收敛。但是，这也会使PSO容易陷入局部最优。为此，将GA的交叉和变异算子引入到PSO算法中，以便将两种算法的优点结合起来，从而更好，更快地获得最优解。为进一步加快优化速度，可通过共享全局最优方法来实现两种算法的独立性和协同操作。具体步骤如下：

1)初始化参数值，包括种群大小(设为1000)，交叉率(0.7)和突变率(0.2)，最大迭代次数(50)。为了避免迭代过程陷入局部最优，同时减小计算时间，这里采用较大的种群规模。同时通过交叉和变异算子来增加群体的多样性，进一步达到避免局部最优，达到全局最优的目的。

2)随机生成n个粒子的初始化种群，并计算所有粒子的目标函数值，寻找并记录个体和全局最优解。

3)将种群分为两组，规模分别为n×P和n×(1-P)，然后分别在这两组中采用PSO算法和GA算法。这里P是混合概率，设为0.3。

4)采用Clerc提出的带约束因子的PSO算法。速度更新公式如下：

v1=wv1+c1·r1·(pi-xi)+c2·r2·(pg-xi)

(6)

φ=φ1+φ2

(7)

c1=wφ1

(8)

c2=wφ2

(9)

与标准PSO相同，这里，vi是第i个粒子的当前速度；r1和r2是0-1均匀分布的两个伪随机数；xi是粒子当前位置，pi和pg分别是微粒的历史最佳位置和粒子群体的全球最佳位置。并且φ1和φ2都设置为2.05。在飞行过程中，粒子的速度受到vmax的限制，定义为

vmax=(xmax-xmin)/10

(10)

这里xmax和xmin分别是自变量的上限和下限。

通过更新的速度和当前位置以获取下一时刻的位置

xi=xi+vi

(11)

根据上式更新位置后，计算所有粒子目标函数值，寻找并记录新的个体和全局最佳解。

5)采用GA算法：采用轮盘赌策略来选择个体进行交叉操作。两个体x1和x2的交叉按下列公式

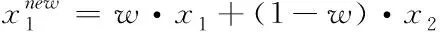
(12)

(13)

突变的粒子是随机选择的，并将变异操作定义如下

xnew=x+w·(xmax-xmin)

(14)

6)将PSO和GA算法过程产生的后代群体组合，并选择适应度值最大的n个粒子形成新种群。

7)重复3)-6)，直到满足最大迭代次数为止。

具体流程图如图1所示。

3.2 模型仿真模拟及优化

为了对交叉口现状信号配时进行仿真评价，本部分利用Synchro系统信号配时优化功能实现。Synchro系统是信号配时优化的专业仿真软件，能够优化信号相位、周期、配时等，并做出信号配时的方案的相关评价。为了分析高低流量对车辆运行的影响，将运用灵敏度分析法进行研究。灵敏度分析即模型中某一影响因素(模型参数或外部环境)发生变化对模型输出的影响程度，常用于模型参数化过程和模型校正。本文在现有交通流量的基础上增加高流量(1.2Q)和低流量(0.8Q)两种情景，讨论不同情景下的评估指标变化。

4 案例研究

案例中选取了武汉某一典型十字交叉口为研究对象，东西南北各进口均设置左、直、右三个专用道，采用包含东西直行、东西左转、南北直行和南北左转典型四相位控制，如图2。信号周期为140s，四个相位的时间分别为56s、23s、35s、26s，各相位时间均有3s黄灯时间、3s启动损失时间和1s红灯时间。

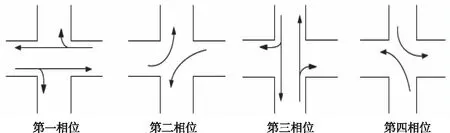
图2 交叉路口相位控制图

此次调查在早高峰时段(7∶30～8∶30)进行，获得的车流量数据如表1所示。

表1 高峰时段交叉口各进口道流量数据

这里东西进口方向的饱和流量为3600PCU·h-1，南北向饱和流量为3200PCU·h-1。

4.1 不同配时方案的比较

实验中首先运用Webster法重新配时计算，然后在Matlab环境下将建立的信号配时优化模型分别运用PS0和PSO-GA算法求解。

将GA算法运用于交叉口时序优化问题，这里GA算法是利用Matlab的Optimization工具箱来求解的。设置GA的初始种群个数为1000，根据个体的适应度值来选择最优解。其中涉及到的选择、交叉和变异操作设置的参数(包括交叉率和变异率)与PSO-GA算法一致，在此不再赘述。此外，实验中函数值精度1e-6，非线性约束为1e-3，初始值(100；0.7)，当迭代到第120代时，实验终止，此时模型的最优解为c=120，x=0.609，迭代过程如图3。

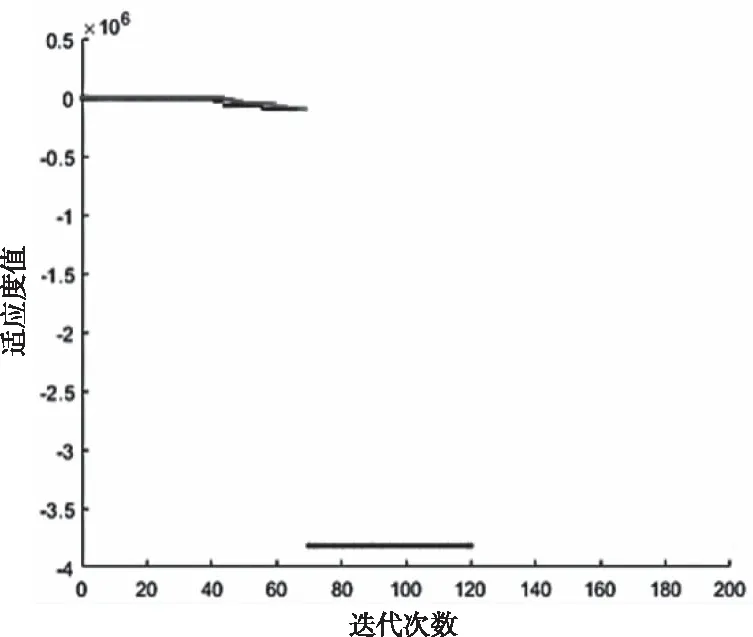
图3 GA的迭代过程

从图3可以看出，GA算法在迭代70次左右才获得最优解，并不会出现太大的波动，迭代120次时寻优结束。整个迭代过程较为平稳，没有出现来回振荡的情况。

然后，将混合PSO-GA算法用于解决信号时序优化问题，按照前一章介绍的PSO-GA的算法流程和参数设置，利用相关程序，得到模型的最佳周期为c=112.6s，迭代过程如图4。

图4 PSO-GA的迭代过程

图4显示了PSO-GA的实验结果。与GA类似，在PSO-GA模型中，适应度值在一开始就保持稳定，然后在第25次迭代后最优解就开始急剧下降，经过36次迭代，就可以获得最优解，而不会产生太大波动。上述特征表明，与GA相比，PSO-GA的收敛速度和稳定性更好。该结果与PSO-GA的优势相吻合，可以更好、更快的获得问题的优质解。

为了评价本文提出模型的性能，将现行配时方案、Webster模型、GA模型和PSO-GA模型的各项交通数据输入Synchro软件得到了一系列的评价指标，数值比较如表2。

表2 多种配时方案的数值比较

由表2可以看出，综合网络性能的各项指标，PSO-GA模型的性能比其它模型更好。特别是周期时长，仅有112.6s，远低于其它配时方案。与现行方案相比，PSO-GA算法获得的周期时长，平均车辆延迟显著减少，其中周期时间减少达19.5%，平均时间延迟为14.5%，通行状况明显改善。与Webster相比，虽然通行能力在减少，但PSO-GA算法获得的周期时间，平均延迟时间也减少了一定程度。此外，与GA相比，PSO-GA获得的通行能力、周期时间和时间延迟均实现了一定程度的改善。虽然相比其它方案，停车次数有一定程度的增加，但所占的比例很小。因此，可以得出PSO-GA算法能够实现更好的性能，满足交叉口配时的需要，并达到更好的效果，是解决交叉路口时序优化问题一种行之有效的方法。

4.2 车流量对道路交通的影响

由于交通流对车辆行驶的重要影响，基于PSO-GA配时模型，运用灵敏度分析讨论车流量变化对于评估指标的影响，由于交通容量的变化十分微小，所以不作具体分析，重点研究对平均时间延迟和停车次数的影响。

表3给出了交通流量增加和减少20%后平均延误和停车次数的变化情况。(括号里为与原有方案相比变化的百分比)

表3 平均延误和停车次数相对现状的变化情况

从表3可以看出1.2Q(原车流量1.2倍)时车辆平均时延增长幅度显著，高达89.36%。0.8Q(原车流量0.8倍)时，平均时间延迟和停车次数的减小幅度却只有20%，这说明高流量状况对道路交通有较大的影响。

上述分析表明，流量增加会加剧交通拥堵，降低车速，使平均时间延迟大幅增加；流量减少能使交通状况有一定好转，加快车速，平均时间延迟和停车次数也都发生一定程度的减少。综上可知，应合理控制交通网络流量，避免产生过高流量，使车辆运行状况得到改善。

5 结论

本文介绍了一种基于PSO-GA的交叉路口信号配时优化算法，它可以使得时间延迟更小，停车次数更少，流量更大。将Synchro交通仿真软件与各种配时方案结合，帮助寻找交通信号配时优化问题的最佳方案。结果表明，对于信号时序优化问题，PSO-GA算法比现有配时方法、Webster模型和GA更具优势，可以有效地获得最优解，使交通状况得到明显的改善。这表明，PSO-GA算法在交通信号控制和优化领域拥有广泛的应用前景和实用价值。文章的最后运用灵敏度分析，讨论了高低流量状况对于车辆运行指标的影响。结果表明，高流量情境下，平均延误时间增加多达89.36%。为此，应严格控制过高流量情况的发生，这对于改善道路交通状况具有重要意义。

对于交叉路口信号配时优化的未来研究可能有以下几个方向。首先，分析更多类型的信号时序交叉点，以测试本研究中提出的方法的适用性。其次，本文没有考虑某些现实世界的约束和动态事件(如事故，紧急车辆，天气情况等)。通过考虑这些现实因素，可将本文研究的理论应用于特定的区域或城市交通网络。最后，未来可以考虑能耗减少的目标。目前能耗问题是运输中的热门话题，而实际解决排放的文献仅占很小一部分，这也是文章未来研究的重点。