电动汽车城际充换电服务网络规划方法与仿真

华远鹏，白宏坤，王圆圆，李文峰

(国网河南省电力公司经济技术研究院，河南郑州450000)

1 引言

电动汽车充换电服务网络为电动汽车的运行提供重要基础支撑系统，其规划是否合理直接影响到后期充换电服务网络的设备利用率、运营效益、服务质量等。至2020年11月新能源汽车已经达520万辆，是2015年的12倍，充电桩为153.9万台，是2015年的23倍，但车桩比却是3.8：1，充电服务依旧不能匹配电动汽车的增长速。由此，为使设计的充电网络规划技术更加有序[1]，需考虑以下三点：

1)对投资建设单位而言，充换电服务网络规划技术可以指导建设单位合理布局充换电设施，避免盲目投资，提升充换电设施利用率，提高投资收益率，增强建设单位投资意愿，促进充换电服务网络高效、清洁、经济、优质运行，减小不同地区充换电服务水平不平衡等问题。

2)对电动汽车用户而言，充换电设施合理地分布于城市、城际之间[2]，意味着更多的电动汽车能够方便的充电，有利于车企与电网更容易实现对接。

3)对电力公司而言，通过合理规划充换电设施建设，避免充换电设施无序建设对配网安全运行影响[3]，提高间歇性能源互补消纳利用[4]，促进“以电代油”的电能替代战略实施，为构建能源互联网打下坚实基础。

当前有不少此方面的研究，文献[5]以住宅区不同居民数量的情况模拟电动汽车数量，同时考虑站址与变电站的距离、费用、数量等条件；针对消纳间歇性能源的问题，文献[6-7]将换电站与间歇性能源发电系统进行联合控制，发挥换电站的储能性能；文献[8]以区域充电的节点电价、用户满意度以及选择道路之间的联系下建立了充电站最优规划模型；文献[9]建立了通过获取的出租车GPS数据建立充电站交互时空路径模型的选址模型。文献[10]提出一种基于行驶路程和消耗电量数的高速路段选址定容模型，同时利用排队论原理分析其运行效率和服务水平；文献[11]考虑了电动汽车充电站的选址定容问题对配电网络和交通网络的影响，建立了成本最小、网损最小的分布式电源选址定容模型；文献[12]利用出行链描述出行特性，体现了充换电服务网络的公共服务特性；文献[13]采用内点仿射尺度算法计算预测模型，预测了一个杭州市可行的最优化的空间布局分布；文献[14]则对电动汽车充电站规划与运营做出研究。

综上所述，虽然诸多学者在充换电站规划方面做了一定的研究，但尚未形成完整、系统的规划模型和方法，其研究内容也多局限于单一区域内充换电站的建设，对于各个充换电站间的互联以及城市间的充换电站互联研究较少。若不能将城际互联间的充换电站进行有效互联，势必会大大影响电动汽车的推动进程。

本文提出以车辆到达热点分布、基于路网与配电网可靠性及停车站场三种城市公共充换电站选址定容充电站规划方法，其次以充电站建设经济收益最大和用户等待时间最小为目标，以节点电压值为约束条件建立多目标规划模型，然后采用NSGA-II算法求解该模型得到帕累托前沿，最后采用优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution)算法对前沿进行排序，进而得到最优规划方案，对城际互联间的充换电站进行有效互联提出有力支撑。

2 充换电站多目标规划方法

2.1 考虑车辆到达热点分布的充电站多目标规划

首先以规划区域的各个时刻总充电需求距之和最小作为充电站规划目标之一，该规划框架如下：

1)总充电需求矩最小

将电动汽车充电需求和为该需求点提供充电服务的充电站的距离的乘积作为充电需求矩。

2)充电站接入配电网成本和建设成本之和最小。

将充电站接入的配变扩容费用、线路新建费用和线路改造费用之和作为充电站接入配网的成本，构建目标函数如下

C1=∑i∈NT～Ti×pi+∑j∈Njlj×pj+∑k∈Nkqk×pk

(1)

式中：Nt为可选配变型号集合，Ti为第i种扩容台数，pi为单个配变造价；Nj为新建线路型号集合，lj为选择第j种新建的线路总长度，pj为单位长度造价；Nk为扩容线路型号集合，qk为第k种线路进行扩容的总长度，pk为单位造价。

充电站建设成本表达如下

C2=∑i∈NC(mia+bi)

(2)

式中：NC为充电站集合；mi为站点i配置的充电机数量，a为充电机单价；bi为充电站建设的固定投资。

3)分布式新能源消纳能力最大

通过将充电负荷与常规负荷叠加，可以改变线路负荷特性，有利于提升分布式新能源消纳能力。

将规划区域的分布式新能源装机量G作为规划目标之一，建立目标函数如下：

maxG=∑i∈BRGi

(3)

式中：BR为规划区域的线路集合，Gi为第i条线路不发生潮流倒送前提下的分布式新能源最大装机量。

4)约束条件

①系统潮流约束

多目标规划模型中，考虑常规的配电网潮流约束如下：

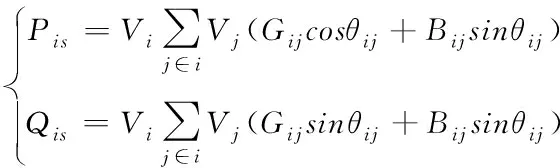
(4)

式中，Pis为节点i的有功注入，Qis为节点i的无功注入，Vi、Vj分别为节点i和j的电压幅值，Gij、Bij分别为节点导纳矩阵的虚部和实部，θij为节点i和j之间的相角差。

②节点电压约束

电动汽车充电站的接入可能导致节点电压降落，危及配电网正常运行，因此设置节点电压约束条件

Ui，min≤Ui≤Ui，max，i∈NL

(5)

式中：Ui为节点i的实际电压值，NL为所有节点集合。

2.2 考虑路网与配电网可靠性的电动汽车充电站多目标规划

本节通过博弈论思想得到电动汽车的行驶特性，进而利用该特性评估城市路网可靠性，通过电动汽车的充放电特性为基准用以测量配电网的供电可靠性；从而进一步，结合充电站综合效益以路网节点为待选站址提出优化方法得到如下规划框架：

1)目标函数

①电动汽车(EV)放电阶段配电网可靠性最大

选取缺供电量作为配电网可靠性评估的指标，该目标函数表示为

maxE1=Edn

(6)

整个区域配电网的缺供电量的表达式为

(7)

式中：Edn，u表示负荷区域节点u的缺供电量

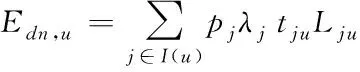
(8)

②综合效益

将电站效益与用户使用成本的年费用作为电站规划的目标函数

maxB=-Psc+Pso+Psr

(9)

式中：Psc为一年建设成本；Pso为一年收益；Psr为结束运行时残值。

3)约束条件

①路网可靠性约束

采用电动汽车用户在选择行驶路径时产生的缺失距离作为城市路网可靠性评估指标

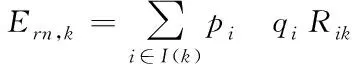
(10)

式中：Ern，k表示缺失距离；I(k)为规划区域路段集合；pi表示破坏者(破坏者是指在路网中使电动汽车在行驶过程产生的缺失距离最大化)攻击i路段后，用户是否改变原有线路的几率；qi表示的是几率；Rik表示用户改变线路后行驶的实际距离与预期需行驶距离之差，其表达式为

(11)

通过确定路网中各节点的线路变化，可以得到电动汽车行驶过程中的城市路网可靠性。所以线路的变化总量可以表示为

(12)

2.3 考虑停车站场的电动汽车充电站多目标规划

将配电网改造的成本计入经济性成本，综合考虑电动汽车充电站规划对交通网络流量、配电网以及分布式新能源的影响，提出如下考虑停车场站的电动汽车充电站多目标规划框架：

2.3.1 目标函数

1)充电设施综合效益最大

①充电设施建设成本年费用

(13)

式中：mj为到达地j的设备个数；a为单个设备数量；bj为到达地j所需投资费用；r为利润率；z为投入使用后年份；N为规划区域内目的地的数量。

②充电设施运营收益年费用

(14)

式中：Ai，j，k为状态标识；Bi，j，k为其充电需求标识；Ci，j，k为其获得充电位标识；Di，j，k为允许接入电网的标识；pEV为单位时段的充电量(kWh/时段)；ei为目的地i提供单位功率充电服务的费用(元/kWh)；nT为一天包含的时段数；nEV为规划区域内私家电动汽车的数量。

③充电设施残值年费用

(15)

式中：ε为充电设施残值对于投资建设成本的折算系数，一般取5%。

综合以上，以考虑充电设施投资和收益以及配电网改造成本的综合年费用最大作为目标函数，表达式为：

maxL=-Wsc+Wso+Wsr+Wsd

(16)

式中：Wsc为充电设施建设成本年费用；Wso为充电设施运营收益年费用；Wsr为充电设施残值年费用；Wsd为配电网改造成本的年费用。

2)分布式新能源消纳能力最大

将规划区域的分布式新能源装机量作为规划目标之一。

3)用户满意度最高

将用户的满意度作为规划目标之一，可以确保充电站的合理运行。

2.3.2 约束条件

设置节点电压约束条件如下

Ui，min≤Ui≤Ui，max，i∈NL

(17)

2.4 规划对比分析

表1 三种规划方案对比

1)从提供公共服务角度出发，在满足规划区域充电需求的前提下，充电站应尽可能靠近充电需求点，使得用户充电服务更加便捷。因此提出了基于车辆到达热点分布的电动汽车充电多目标规划方法。热力图最常用于对某区域温度分布的描述，在热力图中，温度较高的区域用暖色调标注，温度较低的用冷色调标注，可以直观的反映区域总体温度分布情况。

图1 车辆到达热力图

到达热点分布的充电站多目标规划与其它两种规划相比更考虑电动汽车用户对充电的需求，其对节点电压的约束条件和以停车场为主的多目标规划基本相同，同时还考虑常规的配电网潮流约束。

2)考虑路网与配网可靠性的电动汽车充电站的多目标规划则结合博弈论相关知识，引入“城市破坏者”确定电动汽车行驶路径，提出了以充电站综合效益最大和EV放电对配网可靠性改善最大为目标并保证路程可靠性和EV充电阶段配电网可靠性的多目标规划方法。可在如图2所示的路网配电网模拟图中引入电动汽车和充换电站进行模拟计算。图中虚线代表配电网中的10 kV线路，实线代表城市道路。A和B 为电动汽车起始点，C为终点。实线交叉点为道路的交叉点，目标为选择节点建立充换电站。

图2 路网配电网模拟示意图

本小节规划和其它两种规划相比更考虑路网与配电网的可靠性，基于该规划设计的充换电站对电网的利用率更佳的同时也能保证用户的及时充换电。

3)本节提出利用停车场资源，对基于交通流量网格化时变统计的城市充电站的选址进行规划。

大量充电站入网，会对配电网的负载带来较大的影响，导致节点电压过低，导致变压器和线路过载，因此需要考虑对配电网进行适应性改造。综合考虑电动汽车充电站规划对交通网络流量、配电网以及分布式新能源的影响，提出了考虑停车场站的电动汽车充电站多目标规划方法。该规划通过整合现有停车场资源节约了用地成本，是一种符合目前充电站规划现状的实用化方法。

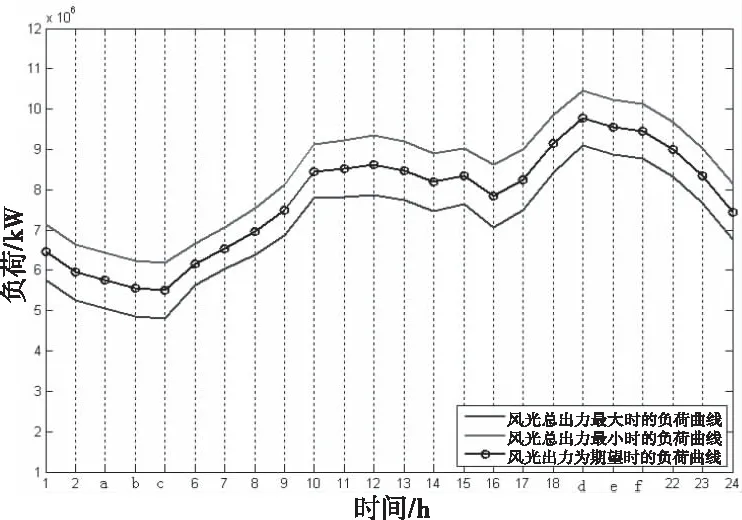
图3 日风光能源输出负荷曲线

如图3中当分布式新能源出力大于常规负荷需求时可能导致线路发生潮流倒送，电动汽车充电站的接入则可以有效消纳新能源发电量，平抑出力波动性，改善负荷曲线。

同时也提出了对配电网的适应性改造，和其它两种规划相比更节约用地成本，适合在高密度的地区中，用户充电使用也会更方便。

3 建立多目标规划模型

电动汽车充电站建设需从多个方面的影响入手，从而得到最优规划。本章模型主要基于两方面即建设需要的经济和用户等待时间。

1)经济方面

充电站建设的经济收益是最重要的目标之一，本文从充电站建设所需成本、维持运行所需成本和配电网改造成本这三方面考虑建设的经济成本。

建设成本C1表达如下

C1=ma+b

(18)

式中，m为充电站配置的充电机数量，a为充电机单价；b为充电站建设的固定投资。

运行维护成本C2表达如下

C2=αC1

(19)

式中，α为折算系数，即运行维护成本正比于充电站建设固定成本。

将充电站接入的配变扩容费用、线路新建费用和线路改造费用之和作为充电站接入配网的成本，构建目标函数如下

C3=∑i∈NTTi·pi+∑j∈Njlj·pj+∑k∈Nkqk·pk

(20)

式中，NT为所有可选配变型号的集合，Ti为选择第i种型号进行扩容的配变台数，pi为其对应单个配变造价；Nj为所有可选的新建线路型号的集合，lj为选择第j种型号进行新建的线路总长度，pj为其对应的单位长度造价；Nk为所有可选的扩容线路型号集合，qk为选择第k种型号的线路进行扩容的总长度，pk为其单位造价。

充电站建设年总成本C为

(21)

式中：z为充电站运行年限。

充电站的年收入可表示为

(22)

式中：n为充电车辆数，Qi为电动汽车剩余电量，p为充电单价。

故充电站建设经济年收益为

maxR=P-C

(23)

2)用户等待时间方面

对于需要充电的第i辆电动汽车，如有充电设备处于空闲状态，则无需等待，可以立刻补充能源，设置等待时间为零，将第i辆电动汽车到达时间记为ti，其结束充电离开的时间为

(24)

对于充电站内充电机都在使用的情形，汽车进入服务区域后则有一段等候时间。对于第q(q=1，2，…n)台充电机，将其充电功率记为p。对于起始电池电量为SOCi的电动汽车，其到达时间记为tc，t，开始充电时刻为ti，其最小平均等待时间为

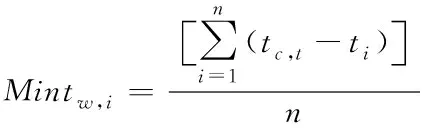
(25)

3)约束条件

当电动汽车充电站接入配电网时，配电网可能因此发生波动，从而可能导致节点电压发生骤降，因此将节点电压设置约束如下

Ui，min≤Ui≤Ui，max，i∈NL

(26)

式中：分别为节点i电压值的下限和上限，Ui为节点i的实际电压值，NL为所有节点集合。

4 基于NSGA-II和TOPSIS算法的多目标模型求解

本文首次采用NSGA-II算法进行多目标优化求取pareto前沿。对于多目标求解得到的帕累托前沿，再采用TOPSIS算法对其进行排序，通过对原始数据的整合归一，求得理论最优解。

1)NSGA-II多目标求解流程

图4是NSGA-II算法的求解流程。这种算法保证了种群密度和数量的多样性，同时所得解为最优解。

图4 NSGA-II算法求解流程

2)TOPSIS排序算法流程

TOPSIS排序算法求解的基本方法[15]就是在Pareto前沿中寻找各项指标函数的最优值，定义为“理论最优解”，同理定义“理论最劣解”。

TOPSIS排序算法的计算流程如下：

1)原始数据归一化处理

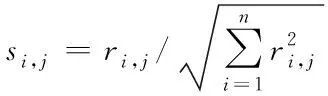
(27)

式中：ri，j、si，j为第i组解的第j个目标函数分别在归一化前后的值，n为Pareto前沿中解的个数。

2)寻找各项目标函数归一化后的最优值和最劣值，得到“理论最优解”(g1，g2，…，gn)和“理论最劣解”(b1，b2，…，bn)，其中gi(i=1，…，n)为所有si，j(i=1，…，n)中的最优目标函数，bi(i=1，…，n)为对应的最劣目标函数值；

3)计算所有解与“理论最优解”和“理论最劣解”之间的距离

(28)

(29)

式中：m为目标函数个数。计算所有解理想度，并对其排序得到最优解

(30)

3)总体规划流程

此处的规划方法首先需要预估区域总体充电站数量z，确定新建充电站的数n。在确定n的前提下，考虑如何将z个充电桩分配到n个充电站，由此生成m组充电桩分配方案。

针对每一组充电桩分配方案，运用图5所示规划流程进行求解并排序，得到该分配方案下的最优规划方案并记录。

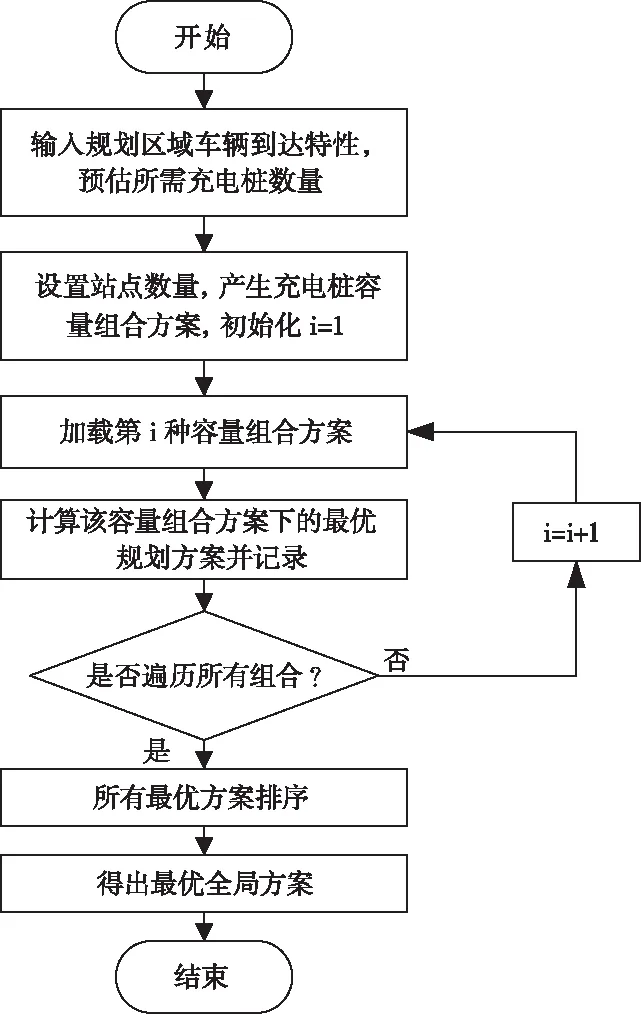
图5 总体规划流程

5 算例分析

在高速公路某服务区规划4个充电站，此处高速公路服务区一天典型车流量分布如图6所示，充电站建设固定成本为200万元，每台充电机单价设置为30万元，运行年限为20年，运行维护费用折算系数为5%。将电动汽车渗透率设置为20%，电动汽车电池容量为40kWh，充电机充电功率为120kW，每千米耗电量0.2kWh。电动汽车剩余电量分布满足电池可用容量的50%(Qmin)-100%(Qmax)均匀分布，则对每小时经过该路口的电动汽车进行抽样。

图6 最优方案日服务汽车数目分布

图6中是最优结果规划结果得到的四个充电站最优规划方案下，每个充电站的日服务汽车数目分布数量，在待规划路段设置的四个充电站，各站之间相距约50公里。其中S1、S2站分别设置了30个充电机；S3、S4站分别设置了20个充电机。

图7是最优规划区域配电网拓扑结构，包括4条10kV线路，线路型号为LGJ-150，19个负荷节点，总负荷约为12.5MVA，每平方公里负荷密度约为2.1MVA。图中S1-S4所示最优规划的4座充电站的位置是为了确保约束条件不变即稳定节点电压。

图7 充电站在配网节点位置分布

充电站所存在并可使用的充电机数量已知时，所建立的收益模型可用于对已知充电机数量的充电站进行建设经济收益的计算，同时将用户等待时间的模型代入，可求得等待时间目标。将充电机数量设置为优化变量，种群大小设置为100，最大进化代数为150代，通过多目标求解流程，得到充电站S1帕累托前沿如图8。如图所知，充电站经济效益与用户等待时间几乎成反比，充电站建设用户需根据自己的需求选择以用户等待时间为建设目标还是以经济效益为目标。

图8 帕累托前沿求解结果

对非劣解前沿进行分析可知，当充电机数量过多或者过少时都无法轻易得出最优方案。因此本文采用TOPSIS排序方法对规划方案的理想度进行从上到下顺序的排列，得到最优的方案。对于充电站S1，利用TOPSIS排序方法对非劣解进行排列，将排名靠前的几个建设方案的按照理想度的高低进行排列，得到的结果见表2。

表2 方案比较

分析可知，充电机数量为34时方案理想度最高，其经济收益优于方案2，但方案2的等待时间较短，实际规划时应当根据实际情况进行充电站的建设。

经过Pareto前沿求解和TOPSIS排序之后可以得到充电站S1的规划方案，同理，对充电站S2、S3、S4再次使用上述方法求解，从而获得4个站各自最优的方案。

在基于城际互联交通流量统计的充换电站选址定容规划数目的基础上，考虑配电网适应性改造对充电站规划带来的影响，采用多目标规划模型和方法进行4座充电站的容量优化，可得优化前后对比如表3所示。

表3 考虑配电网改造前后方案对比

表3可以看出，考虑配电网的改造成本后，S1、S2两个充电站的充电机台数比原来未考虑配电网的情况下增加了，但S3、S4的充电机台数却减少了；由于配电网改造需要消耗大量资金，四个充电站的年收益比优化前都有所减少。

如表4的多目标规划方案比较结果。站点S1充电机最多，同样，等待时间也最短；站点S2的充电机有32台，其经济收益最多，达到了46.23万元；S3和S4的充电机都是17台，等待时间S3比S4稍长，经济收益高出约2万元。由此用户可根据目标侧重点不同选择适合节点建设充电站方案，即：以经济成本和用户等待充电时间为目标进行规划。

6 结论

本文首先提出以车辆到达热点分布、基于路网与配电网可靠性及停车站场三种城市公共充换电站选址定容充电站规划方法，将三种方法从规划方案上进行对比，再综合考虑了充电站建设的经济性和服务能力，经济上考虑充电站建设成本、维持运行成本和配电网改造成本三方面，而服务能力主要从用户等待时间方面进行考虑。综合考虑充电站规划对配电网的影响、对于新能源消纳的影响、交通流量的影响，以充电站年平均建设成本和用户充电平均等待时间两个方面为目标，建立了充电站的多目标规划模型，采用NSGA-II多目标算法对规划模型进行求解得到帕累托前沿解，并用TOPSIS算法对帕累托前沿解进行排序，可得最优方案。最后通过算例分析中规划的高速公路某服务区4座充电站进行的多目标规划模型方法容量优化结果验证本文所用方法的有效性和实用性。结果表明：用户可分别从经济收益和用户等待时间角度考虑，不同的侧重点会出现不同的结果，两者不能兼得，但在考虑配电网改造成本下年收益将有所减少。