突发事件下的航路网络通行能力研究

2022-02-09王莉莉谢昊松

计算机仿真 2022年12期

王莉莉，谢昊松

(中国民航大学空中交通管理学院，天津300300)

1 引言

随着民用航空运输业的持续发展，持续增长的空中交通流量所带来的空域紧张、航班延误等问题逐渐显露，据《2019年民航行业发展统计公报》指出2019年全年客运航班平均正常率为81.65%，可见突发事件导致的航班延误将愈发严重。繁忙空域内不仅承载着日益增加的航班流量，还面临着随之而来的交通流量压力，通行能力的高低直接决定了民航的运行效率。对于空管部门而言，在不超过容量限制的前提下，关注的是让繁忙空域的航路网络流量分布更为均衡，从而降低管制员的工作负荷，提高管制工作的安全水平。航路是一切空中交通活动的载体，而交通阻抗和网络流量是影响航路网络交通态势的主要因素，面对既有的航路网络结构，通过均衡分配网络流量来优化网络的通行能力，从而使得整个网络处于高效运行是亟待研究的问题。航空运输系统是一个复杂系统，网络化是航空运输系统的必然趋势。此外，复杂网络理论对于网络的时空演化规律有着很好的把握，为网络的抽象建模和量化航路阻塞强度提供了新思路。

对于航空网络拓扑结构复杂性，Cheung等[1]针对美国航空运输网络的网络特性进行分析，结果表明其航线网络具有小世界网络特性，度分布服从双段幂律分布。王姣娥等[2]通过对国内航空网络的实证研究，揭示了中国航空网络空间结构的复杂性。Bertsimas等[3]研究了容流不匹配情况下的航路网络通行能力，提出了一种离散优化模型用于公平地分配延误。杨尚文等[4]以总航班延误损失最小为目标函数，建立了三种鲁棒优化模型来分配交通流量，并采用国内机场实际运行数据构造算例，进一步验证了模型和算法的有效性。田勇等[5]重点分析了航空恶劣天气对扇区通行能力的影响，通过结合民航规章制度、管制员工作负荷以及扇区构型等多方面因素，提出了扇区通行能力计算方法。王宽等[6]指出交叉点是空中交通运行的瓶颈，考虑飞机速度、机型组合、航线夹角对通行能力的影响，建立了交叉点通行能力的计算模型。王莉莉等[7]考虑航路容量、管制员负荷等因素，通过排队论构建了交叉点与航路的阻抗函数，提出了一种改进的Dial算法来优化航路网络通行能力，从而缓解网络拥挤。

在研究航路网络通行能力时，以往研究侧重于空域用户的出行时间最短，但空中交通网络是一个复杂系统，如果所有空域用户都选择的初始出行时间最小的路径，这条路径的出行阻抗随着流量的增加而增大，伴随着拥堵的产生，该路径将不再是最省时的路径。

综上，针对以往研究中存在的空白，考虑了网络中的阻塞流动对航路容量的影响和航路阻抗随流量动态变化的特点，本文将复杂网络理论同空中交通配流问题相结合，使优化后的容流更加匹配，为改善网络通行能力以及降低航班延误提供决策依据，这个角度是管制部门更为关注的。

2 基于阻抗函数的通行能力调配优化模型

2.1 航路网络的抽象

航路网络作为复杂网络的一种，能够对其使用复杂网络理论中图论的方法进行抽象，可以将航路网络抽象为图G=(V，E，W)。

V表示航路交叉点、导航台的集合。文献[9]中将VOR导航台视为航路网络中的节点，但航路网络的交通态势主要是由航路交叉点确定的，所以进一步修改为将交叉点、导航台视为节点，从而使模型更贴近实际运行。

E表示航路网络的边集。文献[10]将其抽象为有向图，本文将航路用有向边eij表示，另外航路网络中不同高度层的航路不存在航路交叉点。邻接矩阵A(n×n)可以表示网络中节点对(i，j)的连接情况，若节点对存在连边，则eij=1；若节点对不存在连边，则eij=0。

W表示航路网络边权重的集合。文献[11，12]以交通流分配理论中的阻抗函数为基础来考虑网络的边权，本文从系统最优策略角度出发，构建航路阻抗函数，用其描述网络中的边权。

2.2 模型的数学描述

网络特性度量指标如下：

1)度及平均度davg

网络中的节点i的度di是指与节点i连接的边的数目。

平均度davg为网络节点间的平均连接的边的数目。

(1)

式(1)中：m表示网络的总边数，n表示网络中节点的总数目。

2)边介数Blh

边介数反映了边在整个网络中的作用和影响力。

(2)

式(2)中：Nij为节点i和节点j之间的最短路径数目，Nij(elh)为节点i和节点j之间最短路径经过边elh的数目。

任一网络结构都有其最大容量，当该结构具有产生阻塞条件时，可能产生的阻塞流动现象不仅会降低容量上限，还将导致通行能力的下降。为描述网络结构本身所具有的这种属性，引入网络阻塞强度的概念。在图论的实际建模中，为了便于将图矩阵化，往往将节点的费用转移至边统一进行考虑，结合复杂网络理论中的节点度和边介数，本文定义网络中连边eij的阻塞强度为

(3)

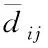
(4)

网络中边上的出行费用一般被称作阻抗函数[13]，见下式(5)

(5)

式(5)中：ta表示航路a上的出行阻抗；t0a表示航路a上的零流阻抗，即航路上流量为零时一架航空器通过该航路所需时间；Fa是航路a的流量；Ca是航路a的容量限制；取ρ=0.15，θ=4。

如果空域存在拥挤时，管制部门将为所有空域用户选择初始出行费用最少的路径，这条路径上的出行阻抗会随着流量的增加而增大，随之产生拥堵。因此随着流量的增加，该路径会被其它出行费用更小的路径所替代，不再是使系统总费用最小的出行路径。因此，模型在考虑上述影响因素后，其目标函数如下

(6)

式(6)中：Z为网络中各航路阻抗之和；fij为i-j航路上的交通流量；t(fij(r))即为各时段r，i-j航路上的阻抗函数，该函数与交通流量成正相关；针对突发事件所导致的航路阻断，引入决策变量φij来表示网络中航路的连通性。

(7)

当航路流量超过其容量限制时，反映在实际航路网络中即某条航路将产生拥堵，故存在下述约束条件

0≤Fij≤Cij

(8)

对于整个航路网络而言，应满足流量守恒约束。即在各时段r各航路上的流量之和等于整个航路网络中的总流量。

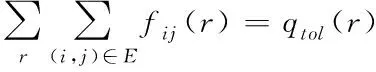
(9)

此外，航路网络中每个节点还应满足流入量等于流出量的约束条件。

(10)

(11)

若J=0，说明航路网络中没有拥堵航路的产生，即网络通行能力水平处于畅通状态；若J=1，说明航路网络中所有航路都发生了拥堵，即网络通行能力水平处于瘫痪状态。

2.3 流量分配算法描述

对于航路网络的期望是，在不超过容量限制且满足总出行费用最小的条件下，给航路网络均衡分配流量。求解网络最小费用最大流问题的经典算法有Ford-Fulkerson算法[14]，但经典算法的静态特性不适应模型中航路阻抗随流量动态变化的特点。配流过程中，航路阻抗将会随着流量的增加而增大，将被其它出行阻抗更小的航路替代。考虑上述因素，为解决交通流量分配过程中航路阻抗动态变化的问题，本文采用一种分阶段求解的近似算法，步骤如下。

(12)

3 算例仿真

3.1 算例构造

图1为中国西部地区部分空域，以其作为仿真空域。红色线段为选取的主干航路网络，由15个节点、20条航段构成，航路网络的平均度为2.67，说明平均每个节点与2.67个节点连接。其中节点1(XIY)，15(KMG)分别为起飞机场和降落机场，高度层配备按照“东单西双”原则，节点3、7、10、11为航路交叉点，其余节点为VOR导航台。航空器在航路上飞行是以向背台形式飞行，节点间的连线则表示本文的仿真航路。图2为起飞机场各时段的离场流量。本文取管制间隔S=15km，安全裕度ΔS=5km。

图1 仿真空域

图2 各时刻离场航空器架次

3.2 突发事件下航路网络通行能力优化及分析

假设因突发事件导致任一离场航路阻断(1-3或1-2航路阻断)，利用MATLAB 2017A对现有空中交通流量进行优化分配求解。

通过离场航路阻断后的拥堵因子变化趋势来表征网络通行能力波动水平，优化前后拥堵因子变化趋势如图3和图4所示。

图3 拥堵因子变化图(优化前)

图4 拥堵因子变化图(优化后)

网络拥堵程度的提升意味着网络通行能力的下降。由上图可知，1-2离场航路阻断所造成的网络拥堵程度大于1-3离场航路阻断。经优化后，1-2航路阻断所造成的拥挤程度有明显下降并呈现曲线波动，这是因为网络中的流量随时间是动态变化，相应导致了航路网络通行能力的波动。管制部门可通过优先保障1-2离场航路上的航班，能使得航路网络通行能力维持在相对较好水平。模型和算法不仅在缓解网络拥堵程度的同时，另一方面也改善了航路网络通行能力水平。

此外，流量分配结果可以有效降低离场航路阻断所导致的延误，优化前后各时段航空器延误水平如图5和图6所示。

图5 航班延误图(1-3航路阻断)

图6 航班延误图(1-2航路阻断)

由计算结果可知，两种离场航路阻断情形下，通过优化使得航空器延误水平分别平均降低9.266%、5.022%。

3.3 TAAM仿真验证

为验证模型可信性，利用TAAM(Total Airspace and Airport Modeller)软件来模拟突发事件下航路网络的通行能力。TAAM建模过程分为静态和动态两方面，其中建立静态模型需要输入机场及跑道信息、进离场程序、航路点信息、扇区划设信息、飞行计划信息等；动态模型建立需要输入冲突解决方案、移交规定、飞行安全间隔等。

图7、图8给出了算例中两种离场航路阻断情形下航路网络通行量仿真结果与其计算结果的对比，通过采用平均绝对百分误差比较二者之间的差异，见下式(13)：

(13)

图7 仿真结果与计算结果对比(1-3航路阻断)

图8 仿真结果与计算结果对比(1-2航路阻断)

由图7、图8可以看出，航路网络通行量计算结果与仿真结果吻合较好，应用式(13)可求出两种离场航路阻断情形下的通行量计算结果与仿真结果的平均绝对百分误差分别为2.6%、7.7%。但总体上航路网络通行量计算值高于仿真值，这意味着突发事件下系统最优调配策略优于传统流量调度方案。因此，本文所建通行能力调配优化模型合理可行。