基于SA优化BP神经网络的室内外无缝定位算法
2022-02-09王伟伟路永乐
刘 宇,王伟伟,邸 克,路永乐
(重庆邮电大学光电工程学院,重庆 400065)
1 引言
随着科学技术的快速发展,研究学者对行人导航定位技术进行了许多研究。目前较为成熟的行人导航定位技术主要有:GPS定位技术[1]、WiFi定位技术[2]、UWB(Ultra Wideband,超宽带)定位技术[3]、地磁定位技术[4]、PDR定位技术[5]、蓝牙定位技术[6]等。由于单一的定位技术无法实现行人室内外无缝定位,因此,提供能够连接室内外环境的无缝定位服务已成为一个关键问题[7]。目前,针对室内外无缝定位技术,国内外许多研究学者进行了相关研究。文献[8]提出了一种基于GPS/WiFi的定位算法,该算法可以减少频繁出入室内外所导致的位置估计所需时间,但是WiFi定位信号不稳定容易受到周边环境的影响,并且WiFi定位需要耗费大量的采集工作。文献[9]提出了一种基于GPS/UWB的融合定位技术,该系统可以实现室内外定位,但是需要提前部署基站,成本高,不易于大范围的推广。文献[10]提出了基于自适应加权算法的WLAN/MARG/GPS组合定位系统,虽然能够实现室内外无缝定位,但算法复杂度过大。文献[11]提出了基于GPS与Wi-Fi的室内外无缝定位原型系统,通过引入alpha-count方法来增加室内外切换的平滑性以及可靠性,但是WiFi指纹定位同样存在数据库采集工作量大。文献[12]提出了GPS/PDR的组合定位滤波方法,利用无迹卡尔曼滤波算法对GPS和PDR数据进行融合,但是由于UKF滤波器采用的假定信号噪声为高斯白噪声,容易导致滤波结果出现偏差。
针对上述问题,本文结合GPS定位技术和PDR定位技术两者的优势,提出了一种基于PDR和GPS的室内外无缝定位系统,并加以仿真验证,从而实现室内外无缝定位。
2 组合定位系统方案
本文研究的基于模拟退火优化BP神经网络的室内外无缝定位方法,整体方案如下:第一,针对GPS和PDR定位结果处于不同坐标系下难以进行融合的问题,在进行数据融合前进行坐标系的转化;第二,建立算法模型,并对其进行仿真;第三,使用模拟退火优化后的神经网络对PDR与GPS定位结果进行室内外融合定位。该方案可以有效降低PDR定位随时间而产生的累计误差,并且解决GPS定位易受外界影响导致定位不连续的问题,实现为行人提供长时间高精度的室内外无缝定位的效果。系统整体方案如图1所示。

图1 系统整体方案图
3 PDR定位
PDR定位算法可以通过惯性测量单元测出的传感器数据结合用户上一时刻状态的位置信息来推算出下一时刻状态的用户具体位置。该方法需要根据步态特征,建立相应的步频、步长估算数学模型。之后,再结合航向角及初始位置这两项相关信息数据进行解算,便可完成位置的递归计算,进一步推算出行人的当前位置,从而进行定位。由于速度的航向信息和姿态信息在行进过程中会出现偏差,这也是导致PDR算法存在累积误差的主要原因。PDR定位算法的原理如图2所示。PDR定位算法的推导公式如式(1)所示。
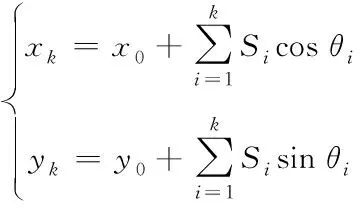
(1)
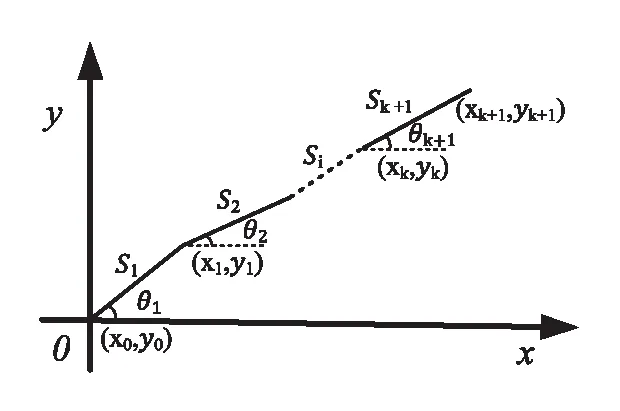
图2 PDR 算法原理图
其中,(xk,yk)为第k步的位置坐标,(x0,y0)为初始位置坐标,Si代表第i步的步长,由步长估计模型获得,θi为第i步的航向。
4 无缝定位算法模型建立
为了优化BP神经网络的权值,加快神经网络的收敛速度以及避免其陷入局部最优解,本文提出了一种基于模拟退火优化BP神经网络的室内外无缝定位算法,对PDR定位结果和GPS定位结果向真实位置坐标方向进行训练,从而获得最优组合定位结果。
4.1 坐标系的转换
在使用BP神经网络对PDR定位结果坐标和GPS定位结果坐标进行训练之前,必须先将GPS与PDR两者的位置坐标转换到同一坐标系下。本文采取将GPS所使用的WGS-84坐标系下的定位结果坐标转换为PDR所使用的东北天坐标系坐标,然后作为BP神经网络的输入。转换方法为:先将GPS的坐标(L,B,H)转换为地球直角坐标(X,Y,Z);再将地球直角坐标(X,Y,Z)转换为东北天坐标(E,N,U)。具体转换公式如下所示

(2)

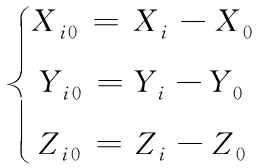
(3)
其中,(X0,Y0,Z0)为行人起始点的地球直角坐标,(Xi,Yi,Zi)为第i时刻的地球直角坐标,(Xi0,Yi0,Zi0)为行人相对起始点的相对位移。
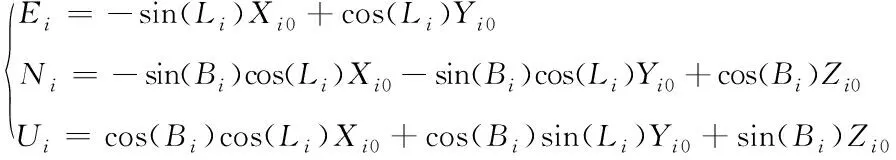
(4)
其中,(Ei,Ni,Ui)为第i时刻的东北天坐标。
4.2 BP神经网络建立
4.2.1 BP神经网络建模
图3是由输入层、隐含层和输出层组成的典型三层BP神经网络。

图3 典型三层BP神经网络
其中,Wij为输入层到隐含层的权向量,Wjl为隐含层到输出层的权向量。
神经网络中各层节点的激活函数设置为最常用的ReLU(Rectified Linear Unit)函数

(5)
用大写字母I、J、L分别表示输入层、隐含层和输出层,用上标in、out分别表示输入和输出,用下标i、j、l分别表示输入层、隐含层和输出层的第i、j、l个节点。
则各层的输入输出分别为

(6)

(7)

(8)

(9)
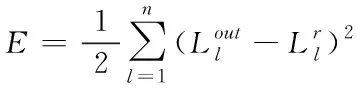
(10)

4.2.1 确定神经元个数
将本文所研究的室内外无缝定位中的PDR定位结果坐标(xpi,ypi)和GPS定位结果坐标(xgi,ygi)作为神经网络的输入层,融合后的坐标作为神经网络的输出层。因此,神经网络的输入层神经元个数为4,输出层神经元个数为2。隐含层的神经元个数根据经验式(11)确定。

(11)
式中,m为隐含层神经元数量,n为输入层神经元数量,l为输出层神经元数量,a为1-10之间的常数。因此,神经网络隐含层的神经元个数设置为8。
4.3 SA 优化 BP 神经网络算法设计
SA 算法模拟固体的退火过程,可以分为:加热、等温和降温三个过程。SA算法在等温过程中可以以一定概率接受部分恶化解,从而避免陷入局部最优解,使得算法最终寻得全局最优解。因此,本文利用模拟退火对神经网络的权值进行优化,从而避免BP神经网络陷入局部极小值,达到对BP神经网络进行优化。算法主要步骤为:
步骤1:算法初始化。
设置初始温度T0,马尔科夫链的长度L,构建BP神经网络,随机设置神经网络的权值并得出初始解向量S0。
步骤2:扰动。
在第k步,根据如式(12)所示的扰动函数由前一个解向量Sk产生新解Sk+1。
f(k+1)=f(k)+ηξ
(12)
其中,η为扰动幅度,ξ为随机扰动变量。
步骤3:计算增量。
计算Sk+1的增量dE=E(Sk+1)-E(Sk),其中E(Sk)为E(Sk)对应的平方误差。
步骤4:Metropolis接收判断
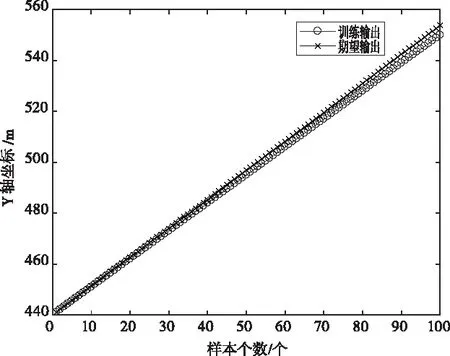
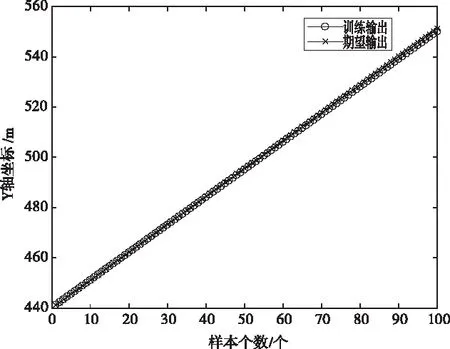
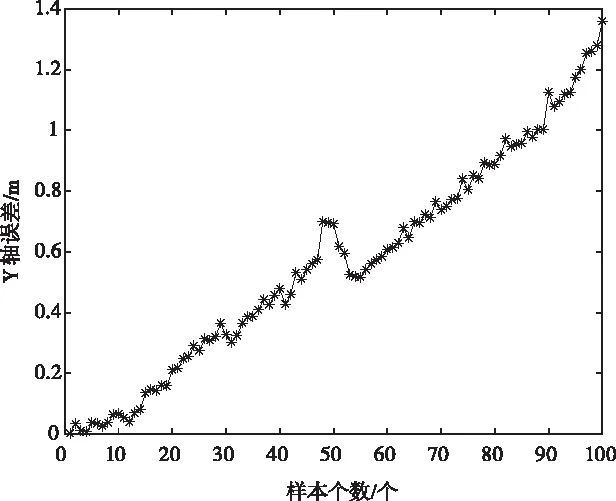
根据如式(13)所示的Metropolis准则判断是否接受新解。如果增量dE<0,则以概率1接收新解。否则首先在区间[0,1]产生一个均匀分布的随机数ε,如果ε (13) 步骤5:内循环终止判断 本文选用时齐模拟作为内循环的判断条件。即将每一温度下的马尔科夫链长度L遍历完时在进行降温操作。 步骤6:降温 本文选用应用较多的如式(14)所示温度衰减函数进行降温操作。 Tk+1=αTk(k=0,1,2,3…) (14) 其中,Tk为温度下降K次的温度,Tk+1为经过一次降温后的温度;α∈(0.5,0.99)中的任一常数。 步骤7:外循环终止判断 本文选用循环总数控制法作为外循环的判断条件。即设定温度下降的总次数,当循环次数达到总次数时,结束算法,否则跳回到步骤2。 最终得到SA优化BP神经网络的算法流程图如图5所示。 图4 SA-BP 算法流程图 为了验证模拟退火算法优化后的BP神经网络的性能,本文使用事先采集好的一组PDR定位和GPS定位的Y轴坐标数据进行融合仿真分析。训练样本采集自场景为GPS信号良好的一条 550m长的直线区域,具体采样规则如表1。仿真时使用的BP神经网络结构为2-6-1,即输入层的神经元节点个数为2个,隐含层的神经元节点个数为6个,输出层的神经元节点个数为1个。 表1 训练数据采样规则 1)未优化的BP神经网络的训练输出及误差 使用未优化的BP神经网络得到的Y轴坐标训练输出和训练误差曲线分别如图5和图6所示。 图5 未优化的BP神经网络训练输出 图6 未优化的BP神经网络误差曲线 2)SA优化后的BP神经网络训练输出及误差 使用SA算法优化后的BP神经网络得到的Y轴坐标训练输出和训练误差曲线分别如图7和图8所示。 图7 SA优化后的BP神经网络训练输出 图8 SA优化后的BP神经网络误差曲线 从图7和图8可以看出,使用SA优化BP神经网络的预测结果更加精确,并且优化后的平均绝对误差为0.568m,而未优化的平均绝对误差为1.837m,预测平均绝对误差降低了约69%,验证了该融合算法的可行性。 为了对本文提出的基于SA优化BP神经网络的室内外无缝定位算法进行验证,选取某室内外场景进行了实验。在进行实验前,先从高德地图获取到实验区域的卫星图,并在图上标出实验行走路线,实验行走路线为A-B-C-D-E-F-G-H-A,其中A-B段和H-A段是室外环境,B-C-D-E-F-G-H为室内环境。具体实验行走路线和实验使用的设备如图9所示。实验过程中,将PDR定位设备固定于行人后腰正中央,GPS固定于行人的右肩,设备采集的数据以txt保存在笔记本电脑上,最后使用MATLAB对采集得到的实验数据进行处理分析,可以得到不同定位方式的结果对比图如图10所示。 图9 实验路线和实验设备图 图10 不同定位方法的结果对比 从图10可用看出,PDR定位方法在一开始拥有较好的精度,但是随着时间的推移,误差不断变大,当回到原点的时候,定位精度已经无法满足定位需求。而SA-BP算法融合得到的定位精度误差随时间的推移变化不大,满足定位需求。 通过对数据进行分析处理,可以得出不同定位方式的平均误差如表2。从下表可以看出,使用 SA-BP 算法处理后得到的定位精度比单一PDR定位精度提升了约55.11%。 表2 不同定位方式的平均误差 为了解决行人在室内外移动定位不连续以及定位精度低的问题,本文提出了一种基于模拟退火算法优化BP神经网络的室内外无缝定位算法。本文所提出的算法具有计算量小和简单易实现的优点。采用SA算法对BP神经网络的权值进行优化,从而避免其陷入局部最优解,并通过仿真验证得到其平均绝对误差下降了约69%,通过实验验证其定位精度可以达到1.089%,较单一PDR定位精度提升了约55.11%。通过使用该算法,可以解决PDR定位累计问题以及GPS定位不连续问题,从而实现行人室内外无缝定位。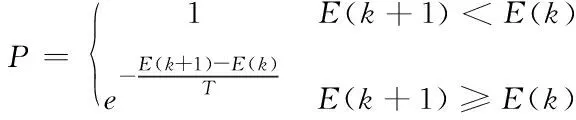

4.4 算法仿真


5 实验验证分析



6 结论
