基于非线性超声检测的搅拌摩擦焊接头疲劳寿命评价

周海鹏，邢松龄，韩赞东，王旭东，沈旭奎

(1.北京轨道交通技术装备集团有限公司，北京 100160；2.北京市基础设施投资有限公司博士后科研工作站/清华大学机械工程博士后流动站，北京 100101；3.清华大学 机械工程系，北京 100084)

铝合金材料具有比强度大、加工性能好等优点，近年来应用广泛，为城市轨道交通车辆的轻量化、高速化设计奠定了基础[1]。搅拌摩擦焊(FSW)是一种适用于铝合金等低熔点合金板材焊接的新型固态焊接技术，与传统熔焊焊接工艺相比具有焊接质量易控、焊接精度高等优点，已经成为近年来铝合金焊接工艺的发展趋势[2]。

焊接接头的疲劳寿命估算是轨道交通车辆疲劳评估的核心内容，也一直是车辆设计与制造过程中的难点[3]。目前一般方法是根据疲劳评估标准，通过有限元仿真计算分析焊缝附近的应力，同时通过动力学仿真或动应力试验获得焊缝区域的载荷谱，基于应力计算结果和载荷谱计算焊缝的疲劳寿命[4-6]。这类评估结果的准确性与模型精度直接相关，结合疲劳试验验证可获得更加可靠的评价结果，但试验成本高、时间长，应用条件受限，基于有限元仿真的疲劳寿命估算结果往往得不到有效验证。

相关研究表明，疲劳损伤引起的非线性效应会导致超声检测信号中出现特殊频率的信号成分，利用非线性超声检测手段可对疲劳损伤进行检测，获取与疲劳寿命相关的检测信号特征，实现疲劳寿命的无损评价[7]。

在疲劳损伤的非线性超声检测领域，国内外学者已取得了多种研究成果。赵立彬[6]采用非线性超声检测对6061铝合金母材及焊接接头的疲劳损伤过程进行了研究，发现可以通过非线性参数来表征疲劳损伤程度；高立等[7]采用超声Lamb波检测技术对5005铝合金板材进行了非线性超声检测，发现Lamb波的频散特性会导致基频幅值波动较大，但二次谐波幅值可用于检测铝板的早期疲劳；李海洋等[8]采用非线性Rayleigh(瑞利)表面波检测方法分别对不同疲劳阶段下Q235钢的拉伸疲劳和腐蚀疲劳试件进行了分析，发现超声非线性系数与疲劳周期数呈单调递增关系，可用来表征材料的表面疲劳损伤程度。

基于上述研究成果，以FSW接头为研究对象，提出了一种基于超声检测的焊缝疲劳寿命估算方法。该方法采用非线性超声检测手段评价焊缝中疲劳损伤的累积程度，根据疲劳寿命与超声检测信号特征的相关关系来评价焊缝的疲劳寿命，具有成本低、可靠性高等优点，可望推动疲劳寿命评价方法的技术发展。

1 疲劳损伤的非线性超声检测原理

超声波在固体介质中的传播可由函数u(x,t)表示，该函数表示传播时间为t、传播距离为x处的声波振动幅度，遵循如下波动方程[9]

(1)

式中：c为超声波的传播速度；f(ε)为关于应变ε的函数，由应力σ与应变ε的关系决定，即

σ=Ef(ε)

(2)

式中：E为介质的弹性模量。

对于线性介质，有f(ε)=ε。受组织不均匀及材料内部微小缺陷影响，超声波的传播介质会表现出非线性效应，即f(ε)中还会出现ε的二次项及高次项，此时f(ε)可根据泰勒公式近似分解为

(3)

式中：β为二次非线性系数，以下简称非线性系数。

超声波一般由单一频率的正弦波激励，在起始位置有如下形式

u(x=0,t)=A1sin 2πf1t

(4)

式中：A1为超声波基波的幅值；f1为超声波的频率。

将式(3)代入式(1)，并将式(4)作为边界条件，可求解得到

u(x,t)=A1sin[2πf1(x/c-t)]-

A2cos[4πf1(x/c-t)]+…

(5)

式中：A2为二次谐波的幅值，可表示为

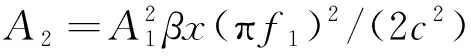
(6)

式(5)中右侧第一项表示基波成分，第二项表示二次谐波成分(其信号频率是基波频率的两倍)，其余项为三次及更高阶次的谐波成分；由于高次谐波的能量占比非常小，非线性超声检测中一般只考虑二次谐波成分。

对于同组超声检测中由不同试件得到的同一处回波信号而言，其传播距离x、基波频率f1及波速c一般不会改变，则有

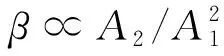
(7)

根据式(7)，可通过测量基波和二次谐波的幅值，分析β的相对大小。

与基于基波的传统超声检测相比，非线性超声检测中的谐波信号对材料中包括疲劳损伤在内的微小损伤更为敏感。材料疲劳过程中会产生微小的疲劳损伤并逐渐累积，由这些疲劳损伤引起的非线性效应也会逐渐增强。因为β可表征非线性效应的大小，所以根据β的变化趋势可分析疲劳损伤的发展过程，进而实现材料疲劳寿命的无损评价。

2 非线性超声检测方案

2.1 检测对象

选取厚度为8 mm，材料为6005A-T6的铝合金挤压板材进行了单轴肩FSW对焊，焊后将焊接接头磨平，按照图1所示尺寸进行取样加工，制备得到FSW焊接试件。

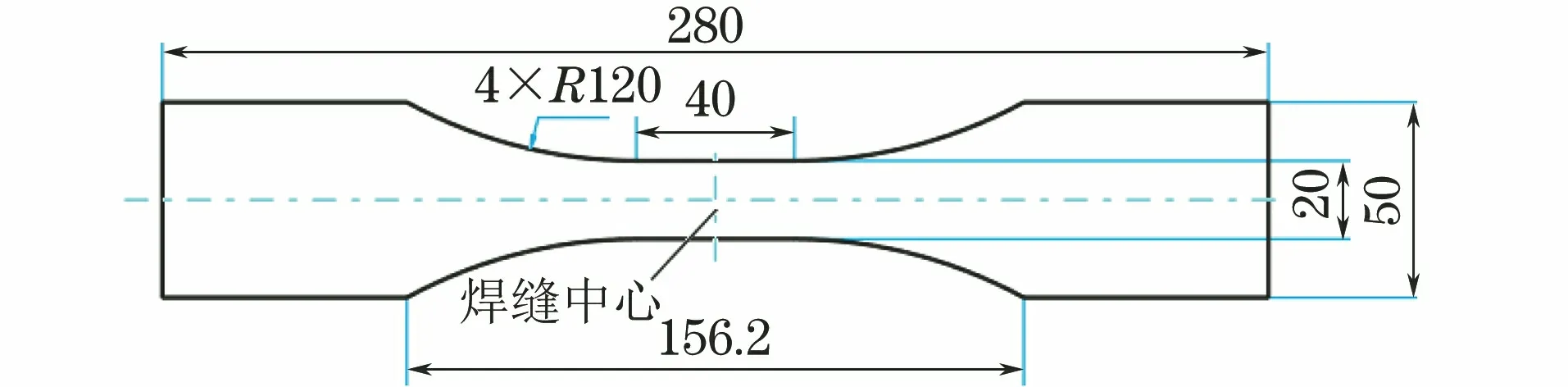
图1 FSW焊接试件尺寸示意

参照标准GB/T 3075-2008 《金属材料 疲劳试验 轴向力控制方法》 对焊接试件进行阶段性疲劳试验，采用正弦变化的交变载荷进行加载，加载频率约为100 Hz，应力比(最小应力与最大应力的比值)为0.1，设置最大应力为120 MPa。取预期疲劳寿命为N0(107次)，将试件分别疲劳至0.1N0，0.3N0，0.5N0，0.7N0，且不出现疲劳失效，即可获得10%，30%，50%，70%寿命的阶段性疲劳试件。每个阶段各获取8个试件，另取8个未疲劳试件记为0%寿命阶段作为对比。对各阶段试件(共40个)进行非线性超声检测，可分析得到检测信号特征与疲劳寿命的相关关系，并据此研究焊缝疲劳寿命的评价方法。

2.2 检测系统

采用RITEC公司的RAM-5000 SNAP型非线性超声检测系统发射和接收超声波信号，同时配合带通滤波器、前置放大器等信号处理模块，提取检测信号的基波及二次谐波成分，非线性超声检测系统结构框图如图2所示[7]。系统工作时，激励信号经5 MHz带通滤波器处理后，由发射探头传播进入试件中；采用宽带探头接收信号，其中基波信号直接传入信号接收器，同时通过10 MHz带通滤波器提取二次谐波信号并传入另一路信号接收器。

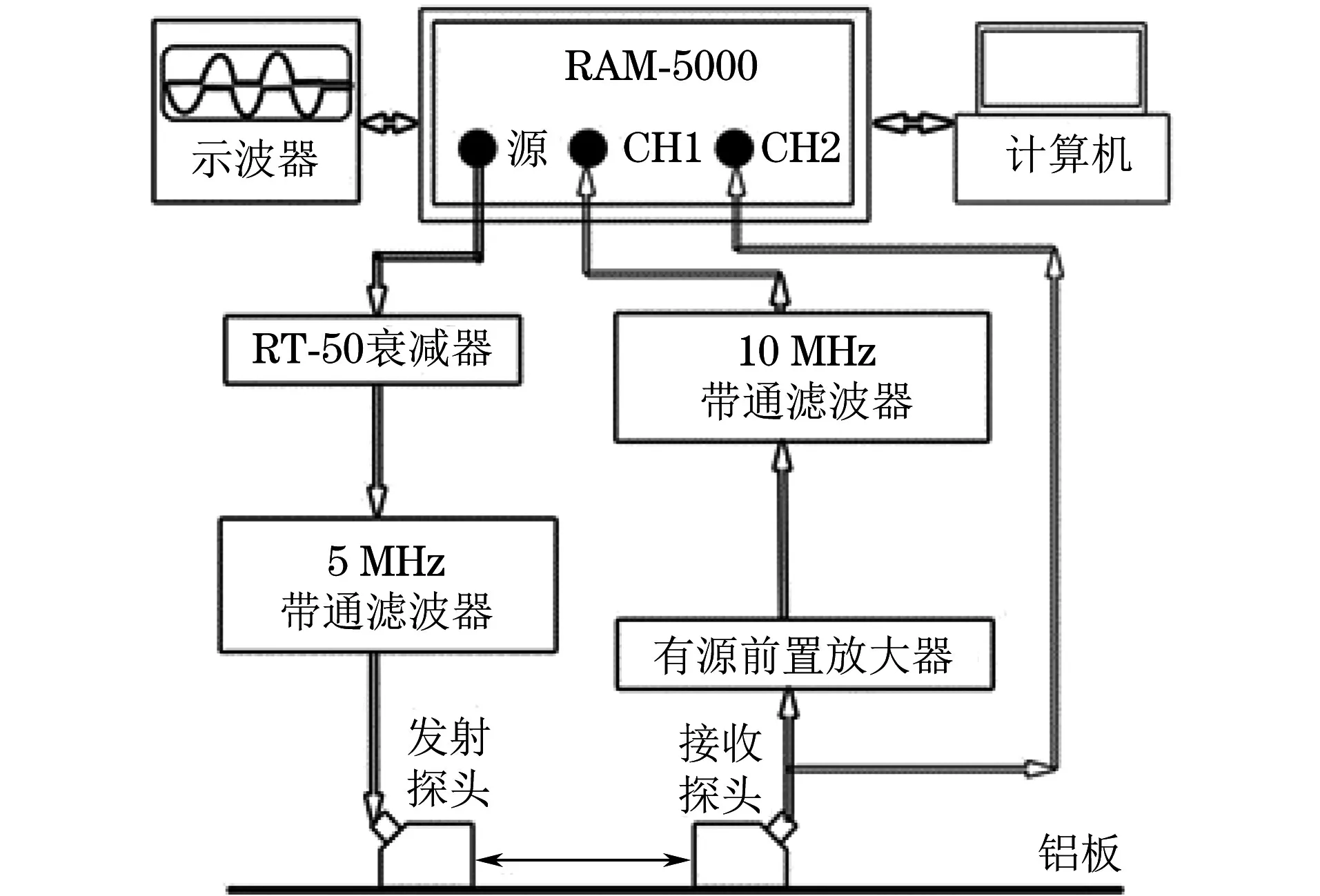
图2 非线性超声检测系统结构框图

采用如图3所示的接触式双斜探头检测方式对阶段性疲劳试件进行检测。定制斜探头的发射角度，使超声波在试件中形成折射角为45°的横波；调整探头位置使两个探头对应的折射点距离为32 mm(试件厚度的4倍)，由此可以接收到超声波在试件内经两次底面反射后的回波信号。

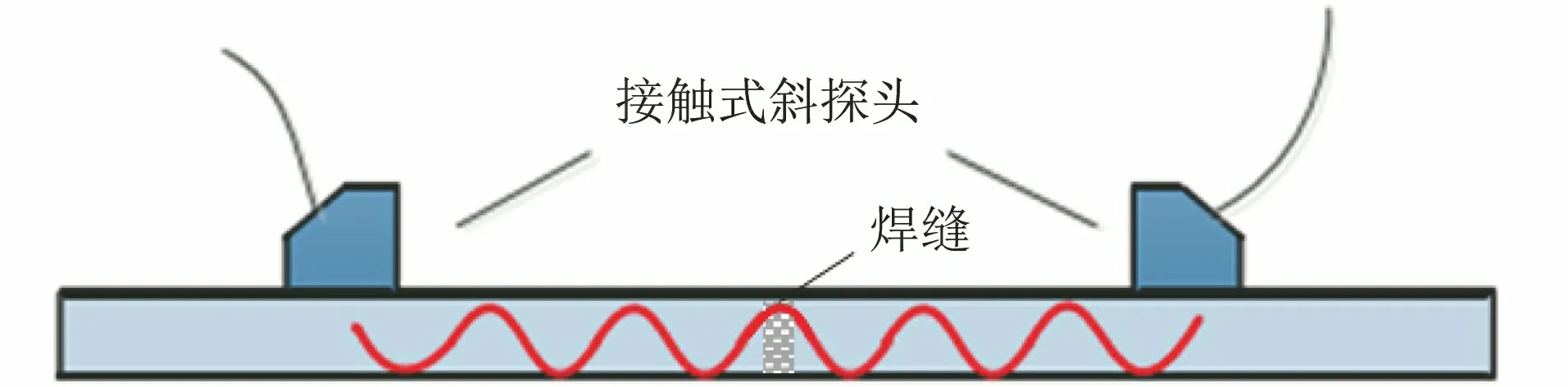
图3 接触式双斜探头超声检测方式示意

3 检测信号特征分析

3.1 信号特征提取算法

采用基于高斯调制脉冲(GMP)模型的信号提取算法[10]对超声检测信号进行处理，检测信号中各回波信号sn(t)可认为具有如下形式

cos[2πfn(t-tn)+φn]

(8)

式中：an为信号幅值；tn为信号传播时间；fn为信号频率；φn为信号相位；bn为带宽因子，与信号的时域波形宽度和频域带宽相关。

采用基于GMP模型的信号提取算法，可将各回波信号表示为控制参数(an,bn,tn,fn,φn)的GMP模型，结合互相关滤波估计各控制参数，实现信号特征提取。文章按照如下流程分析检测信号，并估计信号的非线性特征。

(1) 对于5 MHz的基波信号和10 MHz的二次谐波信号，分别按对应的控制参数生成GMP模型作为参考信号(a0,b0,t0,f0,φ0)，其中b0根据信号特点估计得到,即

① (a0,b0,t0,f0,φ0)5M=(1,0.4,0,5,0)；

② (a0,b0,t0,f0,φ0)10M=(1,0.4,0,10,0)。

(2) 计算检测信号与参考信号的互相关滤波，提取滤波信号最大值出现的时刻作为tn的估计值，根据tn处回波信号的时域与频域特征估计an和fn；基波信号取n=1，二次谐波信号取n=2，分别估计以上信号特征。

(3) 校核f1是否在5±0.5 MHz范围内，f2是否在10±1 MHz范围内，如超过该范围则认为信号提取有误，需要复核信号提取流程。

(4) 根据超声波的衰减规律，仅考虑扩散衰减的情况下，超声波(球面波)的声压幅值与传播距离成反比，笔者对信号幅值进行近似校正，即

An=an/tn,n=1,2

(9)

式中：an以mV为单位；tn以μs为单位进行无量纲处理，计算结果无量纲。

(5) 根据式(7)，计算等效非线性系数βe，估计信号的非线性特征，即

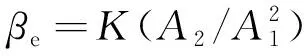
(10)

式中：比例系数K取40。

3.2 FSW焊接试件检测信号特征

以0%寿命阶段的某一试件为例，5 MHz和10 MHz检测信号中的典型回波与选用的参考信号波形如图4所示。由图4可看出，参考信号与检测信号的相似度较高，可获得较好的滤波效果。

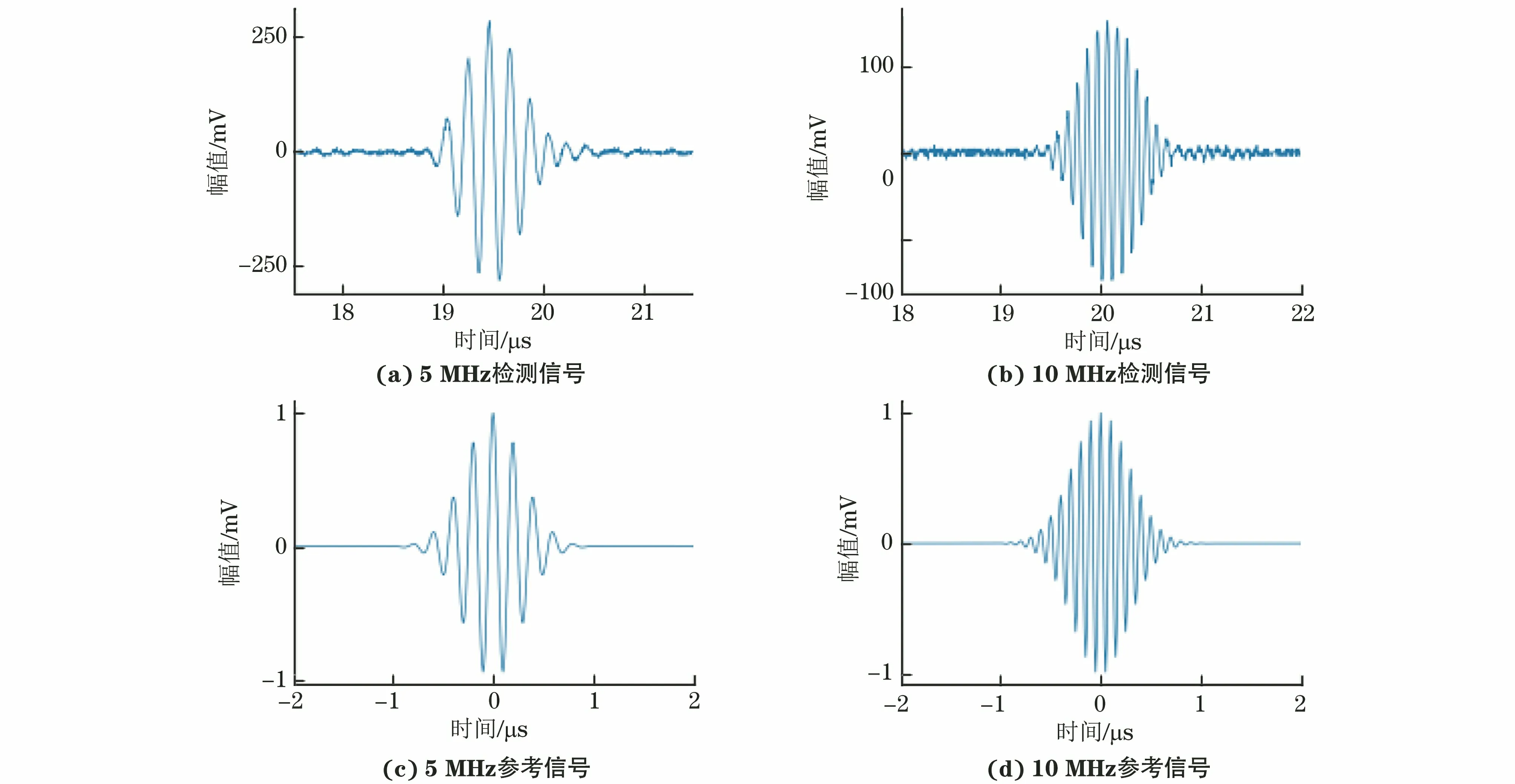
图4 5 MHz和10 MHz参考信号与检测信号波形(以0%寿命阶段为例)

按照前述算法，根据各阶段试件检测信号计算βe，可得到βe与各疲劳阶段的相关关系(见图5)。由图5可以看出，βe随着疲劳次数的增加而逐渐增大，不同疲劳阶段的βe具有一定的区分度。

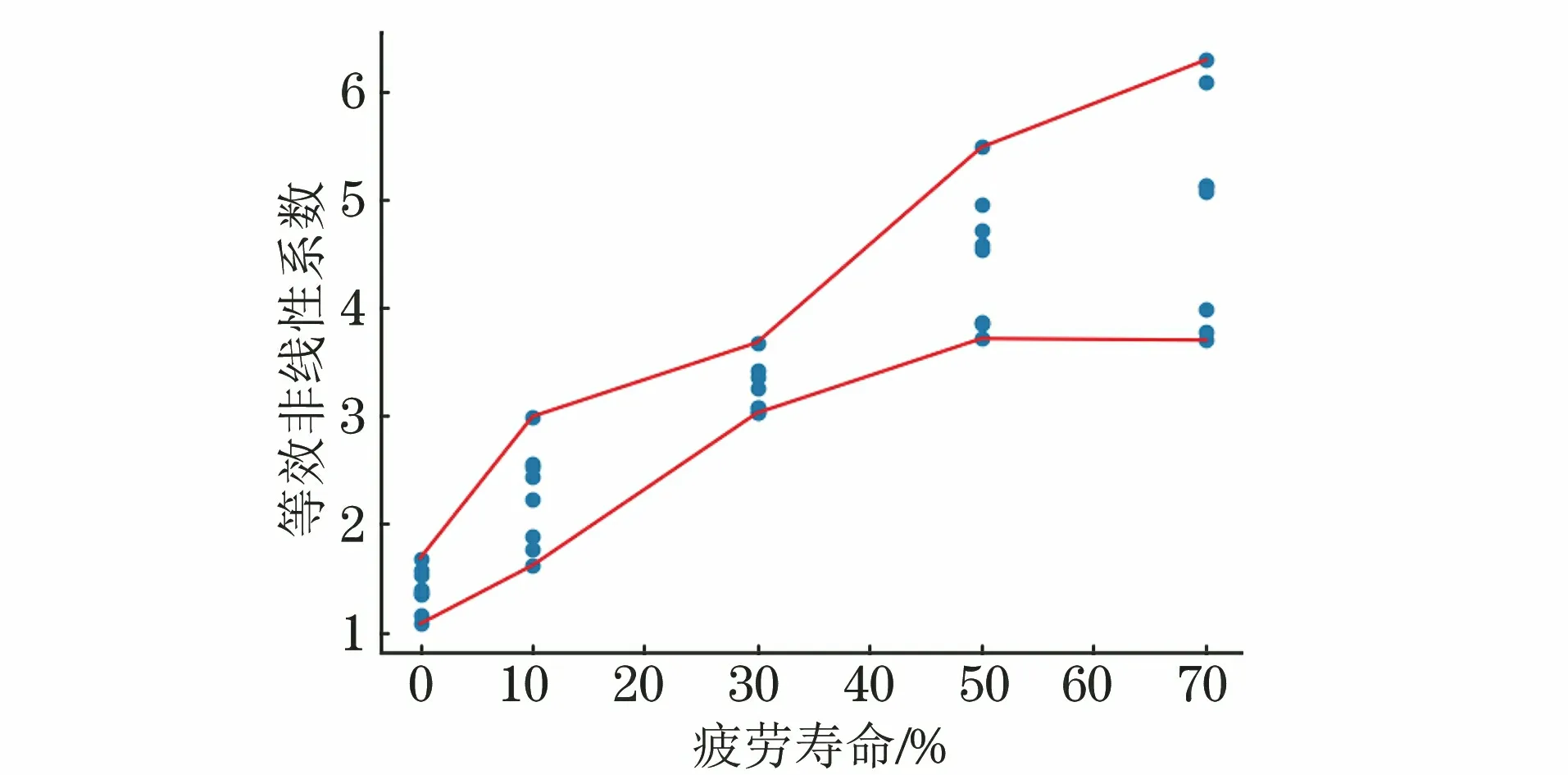
图5 βe与各疲劳阶段的相关关系曲线

4 FSW接头的疲劳寿命评价方法

4.1 贝叶斯定理

根据各疲劳阶段的βe数据分布规律，分析可得到任一FSW接头处于各疲劳阶段的可能性，由此即可实现焊缝疲劳寿命的评价。该评价需要估计某一βe=x的焊缝处于疲劳阶段i的概率P(i|x)(i=0%寿命, 10%寿命, 30%寿命, 50%寿命, 70%寿命)，这实际上是一个基于给定指标的分类问题。

根据贝叶斯定理，P(i|x)可称为后验概率，有如下关系[11]

(11)

式中：P(x|i)称为先验概率，表示已知焊缝处于疲劳阶段i时，该焊缝的βe值等于x的条件概率；P(i)称为分类概率，表示疲劳阶段i出现的概率；可假定各阶段的分类概率相等。

由于总体样本的数据分布情况未知，这里假定各疲劳阶段的P(i)相等，因此通过P(x|i)即可求得P(i|x)；而估计P(x|i)则需要由各疲劳阶段FSW接头的βe构成基础数据库，分析βe的分布规律。

4.2 基础数据库构建

焊缝疲劳寿命的评价需要基于完备的基础数据库，保证每条焊缝都一定处于数据库中的某一阶段。对前述各疲劳阶段所代表的疲劳次数范围做如下扩展性说明，即可形成完备数据库：① 0%寿命——疲劳次数≤0.05N0；② 10%寿命——0.05N0<疲劳次数≤0.2N0；③ 30%寿命——0.2N0<疲劳次数≤0.4N0；④ 50%寿命——0.4N0<疲劳次数≤0.6N0；⑤ 70%寿命——疲劳次数>0.6N0。

一般而言，随机变量应服从正态分布，但在样本量较小的情形下，可改用t分布描述随机变量的分布情况。疲劳阶段i的样本数量为ni，则P(x|i)可表示成自由度为ni-1的t分布概率密度函数，即[12]

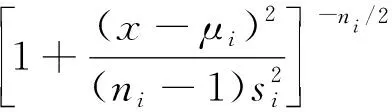
(12)

式中：μi和si分别为βe在疲劳阶段i时的平均值和标准差；Γ(z)为Gamma函数。

将疲劳阶段i中第j个样本的βe参数值记为βij，则μi和si可按照以下方式估计

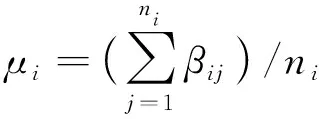
(13)

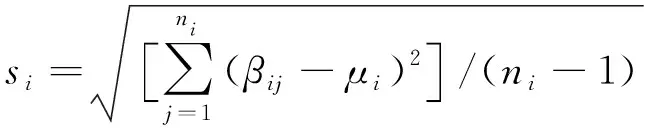
(14)

图5所示的βe值可构成FSW接头基础数据库，其统计信息如表1所示。由式(12)得到βe在各疲劳阶段的概率密度分布函数(见图6)，进而可根据式(11)计算得到βe在各疲劳阶段的后验概率曲线(见图7)。

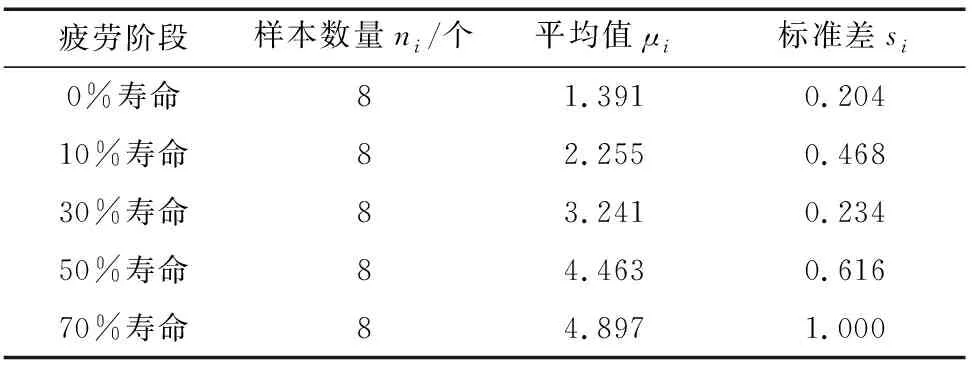
表1 FSW接头基础数据库

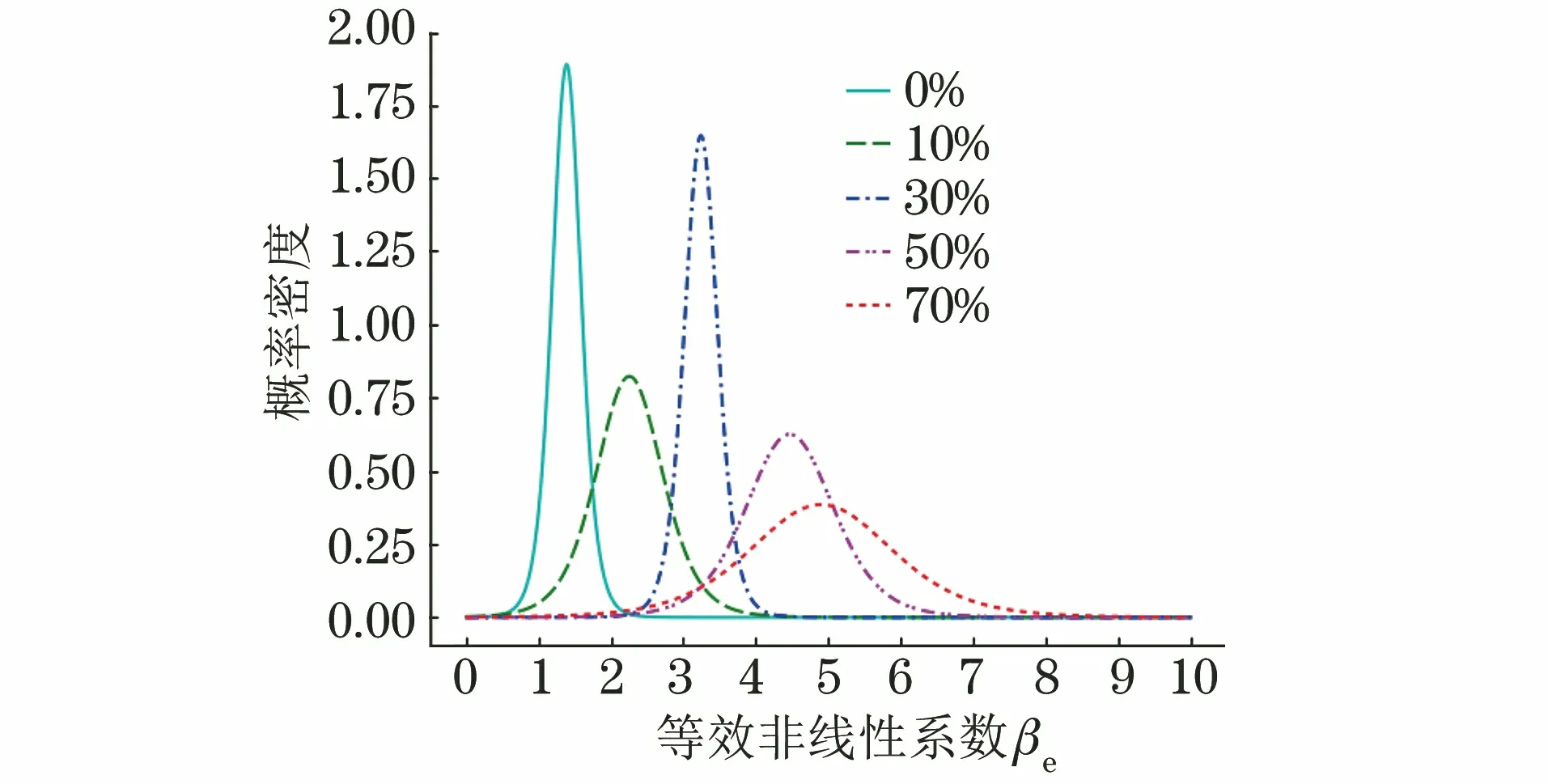
图6 βe在各疲劳阶段的概率密度分布函数

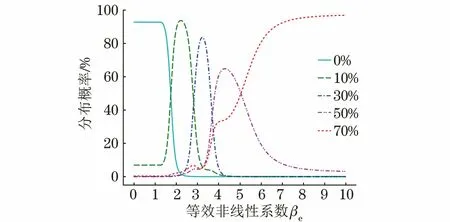
图7 βe在各疲劳阶段的后验概率曲线(可靠范围1.0<βe<6.3)

分析上述结果可知：①βe≤3.5时，焊缝可能以较大概率处于0%寿命，10%寿命或30%寿命中的某一疲劳阶段；② 3.5<βe≤5.5时，由于50%寿命与70%寿命阶段的数据重叠较为明显，焊缝处于这两个疲劳阶段的概率相近；③βe>5.5时，焊缝大概率处于70%寿命阶段。

需要注意的是，样本数据范围是1.0<βe<6.3，超出此范围的焊缝无法获得可靠的评价结果，图7中超出此范围的概率值仅供参考。

4.3 疲劳寿命评价

针对某一类已建立基础数据库的FSW接头，可通过非线性超声检测及信号特征分析获取其βe值，并根据该值估计该焊缝在各疲劳阶段的后验概率，评价焊缝的疲劳寿命。以βe=1, 2, 3, 4, 5, 6的各条焊缝为例，笔者由图7中的后验概率曲线得到相应各焊缝的疲劳寿命评价结果(见图8)。

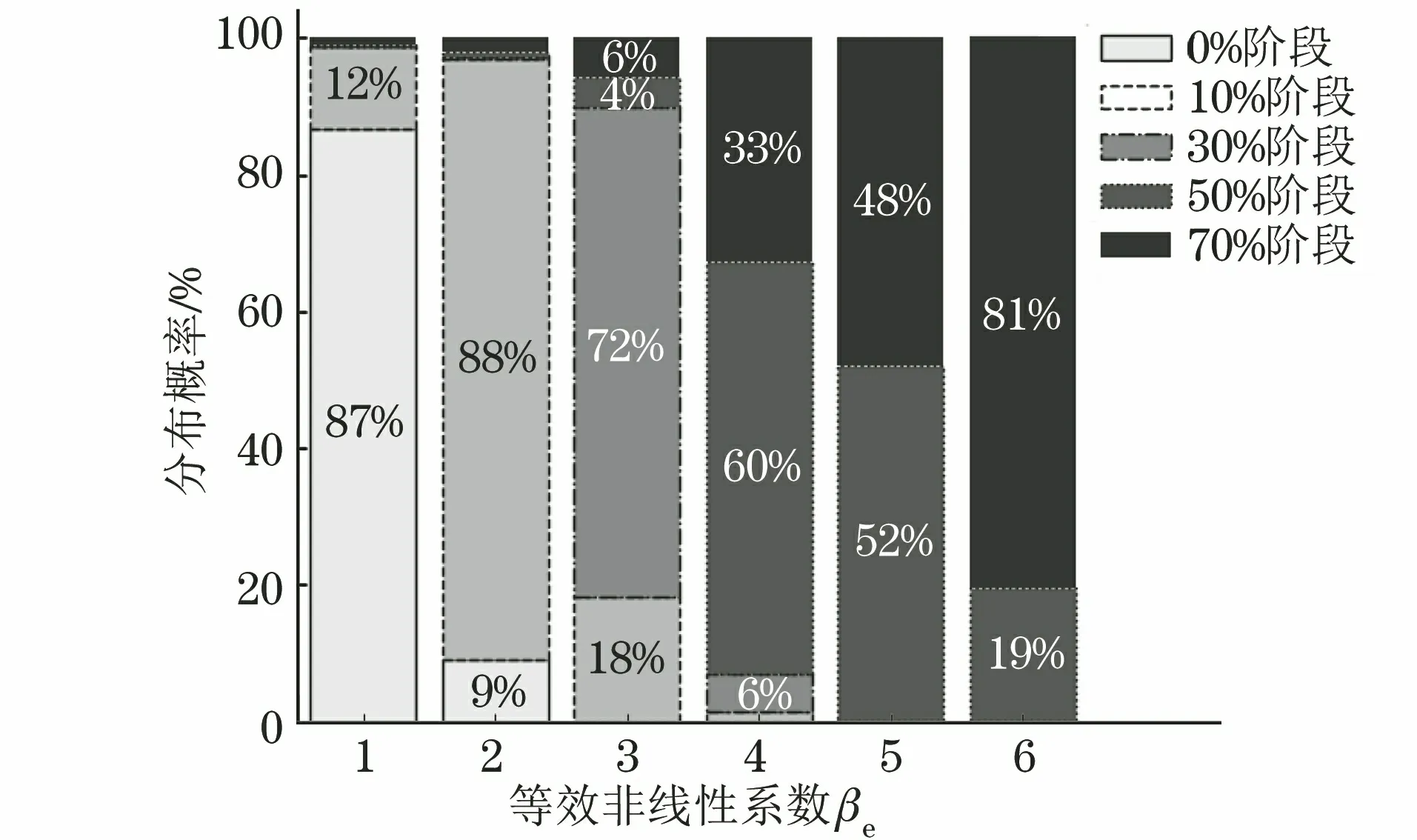
图8 FSW接头不同βe焊缝的疲劳寿命评价结果

5 结论

提出了一种基于非线性超声检测的FSW接头疲劳寿命评价方法，该方法采用接触式双斜探头对FSW接头进行非线性超声检测，通过分析信号特征获取等效非线性系数βe，构建包含多个疲劳阶段的基础数据库，基于贝叶斯定理估计焊缝处于各阶段的后验概率，评价焊缝的疲劳寿命，主要结论如下。

(1) 不同疲劳阶段FSW焊接试件的非线性超声检测信号特征表明，βe参数随着疲劳次数的增加逐渐增大，该参数对各疲劳阶段具有一定的区分度，可用于疲劳寿命评价。

(2)βe在各疲劳阶段的数据分布规律表明，在数据有效范围(1.0<βe<6.3)内的大部分区间上，βe对各阶段的区分度较好，根据βe可判断焊缝大概率处于哪一个疲劳阶段；其中3.5<βe≤5.5时，由于50%寿命与70%寿命阶段的数据重叠较为明显，焊缝处于两种阶段的概率相近。

(3) 提出的评价方法可估计焊缝处于各疲劳阶段的可能性，最终给出焊缝处于各阶段的后验概率作为评价结果，可作为焊缝分类的参考；但是焊缝分类的具体策略还需要结合大量补充试验进行设计和验证。

本文获“2022 Evident杯超声检测技术优秀论文评选”活动一等奖。