面向交通排放测算的跟驰模型优化方法

江 婕，宋国华，孟冬利，彭 飞，于 雷

（北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044）

0 引言

“双碳”目标背景下，正确评估道路交通温室气体等污染物排放是交通运输碳减排政策制定与实施的重要前提。在交通碳减排措施的环境影响评价中，以车辆跟驰模型为核心的微观交通仿真与交通排放模型的融合在交通排放测算研究中得到了广泛应用。微观交通仿真模型仿真生成的逐秒轨迹常被作为微观车辆排放模型的输入进行排放测算[1]，该融合方法被广泛地应用于交通排放评价[2-5]、交通政策评价[6-7]以及交叉口优化[8]等研究领域。然而，利用微观交通仿真模型输出逐秒的车辆行驶轨迹存在一定程度的不确定性，导致其在融合交通排放模型测算交通排放时存在系统误差。因此，有必要针对微观交通仿真模型提出优化方法，以提高交通排放测算精度。

目前，交通仿真模型和交通排放模型融合时，以车辆比功率（Vehicle Specific Power,VSP）作为中间变量解释车辆行驶轨迹特征对排放的影响。由于VSP 对加速度变化的高敏感性，跟驰模型生成轨迹所产生的不真实的加速度会导致计算VSP 时出现明显错误，这也是交通仿真模型应用于排放测算时产生误差的根本原因[9-10]。Viti 等人[11]指出，以VISSIM 默认参数输出的轨迹与真实的轨迹相差甚远。Song[12]和张嫣红等人[13]指出，在使用交通仿真模型来表示逐秒的驾驶行为时存在系统误差，且这种误差不能通过调整仿真模型的参数来降低，需要进一步从模型本身的仿真机理上分析误差产生的原因。针对这一问题，Song等人[9]通过优化状态阈值参数和最大加速度模型，将跟驰模型用于交通排放估计的误差降低了4%。Lu 等人[10]基于Wiedemann 平面设计了一个数据驱动模型，以提高交通排放测算的精度。Meng 等人[14]面向排放测算提出了一种包含多维随机特征参数的Newell 跟驰模型。Wiedemann 跟驰模型是微观交通仿真模型的典型代表，该模型将驾驶员受到的刺激抽象为跟驰车辆前后之间的相对运动，且这些刺激只有超过模型阈值才会引起驾驶员的注意，进而采取相应措施[15]。该模型跟驰域结构离散，生成的加速度“振荡”变化，而在实际的驾驶过程中，车辆的加速度是平稳变化的，基于此衡量加速度变化快慢的变量急动度（jerk）被提出[16]。从物理意义上来说，jerk 是衡量驾驶员踩油门速度快慢的物理量，与驾驶行为有着密切的关系。Ge 等人[17]提出了一种考虑jerk 的最优速度跟驰模型的优化方法，并且Zhai 等人[18]也在此方法上证明了jerk 对交通流和排放的稳定性有显著的影响。

综上，现有面向排放测算的跟驰模型优化方法主要存在以下问题：①优化方法主要是围绕加速度仿真异常提出，模型内部生成不合理加速度的原因并未得到完全解释；②优化后的微观交通仿真模型生成的车辆轨迹用于交通排放模型仍存在较大误差；③优化方法未考虑影响加速度变化的关键参数jerk，Wiedemann 模型无法真实刻画实际驾驶过程中jerk的变化情况。

因此，本文将基于实际车辆轨迹数据，分析jerk 的分布规律以及与加速度的关系，通过增设jerk 约束的方法优化Wiedemann 跟驰模型，改善模型输出的不真实加速度，增强现阶段微观交通仿真模型应用于道路交通排放测算的适用性和准确性，为交通碳减排措施的环境影响评价提供依据。

1 问题描述

Wiedemann 跟驰模型是生理-心理跟驰模型的代表，是微观交通仿真模型的核心。在交通排放测算时，Wiedemann 跟驰模型输出的轨迹数据可作为排放模型的输入进行测算。Wiedemann 模型仿真输出轨迹速度及加速度变化如图1 和图2所示。可以看出，该模型输出轨迹存在明显不真实的速度和加速度，整体呈“跃迁”式变化。这是因为模型生成加速度由离散化的跟驰域决定，而跟驰域仅与车辆的间距差和速度差有关，未考虑加速度变化阈值。

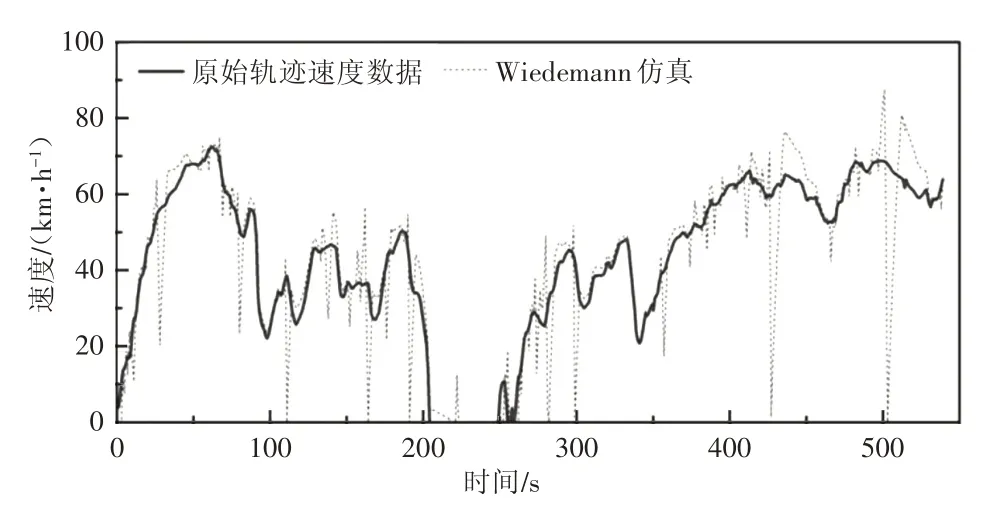
图1 Wiedemann模型仿真与原始轨迹速度对比

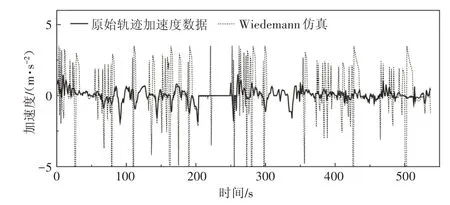
图2 Wiedemann模型仿真与原始轨迹加速度对比

以VSP 为交通排放测算的中间参数，将车辆轨迹数据与排放数据进行耦合，VSP 计算公式如式（1）所示。

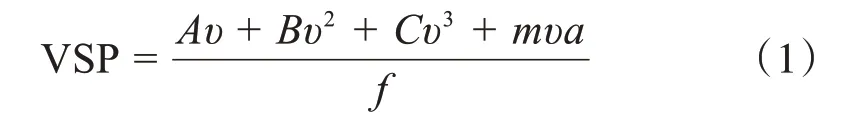
式（1）中：v 为车辆瞬时速度（m/s）；a为车辆瞬时加速度（m/s2）；A为车辆滚动阻力系数（kW·s/m），轻型车取值为0.156 461；B为旋转滚动阻力系数（kW·s2/m2），取值为0.002 001 93；C为空气阻力系数（kW·s3/m2），取值为0.000 492 646；m为车辆与负载总质量（t）；f为换算系数。

从式（1）可以看出，VSP与车辆轨迹中的速度、加速度密切相关。由于Wiedemann 跟驰模型输出轨迹数据的异常，导致VSP 计算结果不准确，进而使得排放测算结果存在较大的系统误差。

因此，将微观交通仿真模型与排放模型融合用于交通排放测算所产生的系统误差本质原因在于微观仿真模型生成不真实的加速度。本文将提出Wiedemann 跟驰模型优化方法，改善模型输出轨迹，进而提高融合排放模型测算交通排放的精度。

2 考虑jerk分布的优化方法设计

2.1 数据采集

本研究使用便携式全球定位系统（Global Po⁃sitioning System,GPS）设备收集了北京市出租车逐秒行驶轨迹数据，包含600 000s 北京市五环内快速路自由行驶轨迹和20 000s 北京市四环快速路跟驰行驶轨迹。自由行驶轨迹用于跟驰模型数值仿真和实际轨迹数据jerk 分布特征分析，跟驰行驶轨迹用于基于速度差-后车加速度平面的跟驰数据分析。

2.2 Wiedemann跟驰模型

Wiedemann 跟驰模型跟驰域对应车辆行驶过程中的4 个不同驾驶状态，分别为跟驰行驶、接近前车、紧急制动和自由驾驶。Wiedemann 模型跟驰域划分如图3 所示，间距-速度差平面中的ABX,SDX,SDV,CLDV,OPDV 等阈值划分出了该跟驰模型的跟驰域[19]。

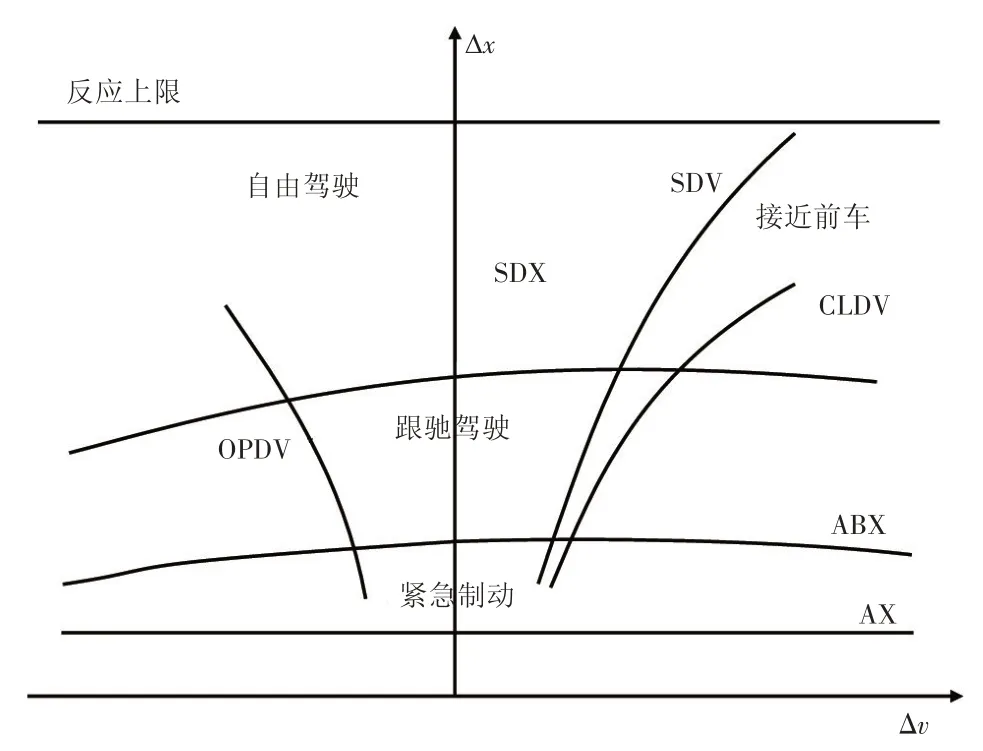
图3 Wiedemann模型跟驰域划分

本研究数值仿真的方法是以实际轨迹数据作为前车的输入，设置初始间距为10m，后车速度与前车一致，模型中各跟驰域边界相关参数取值如表1所示。

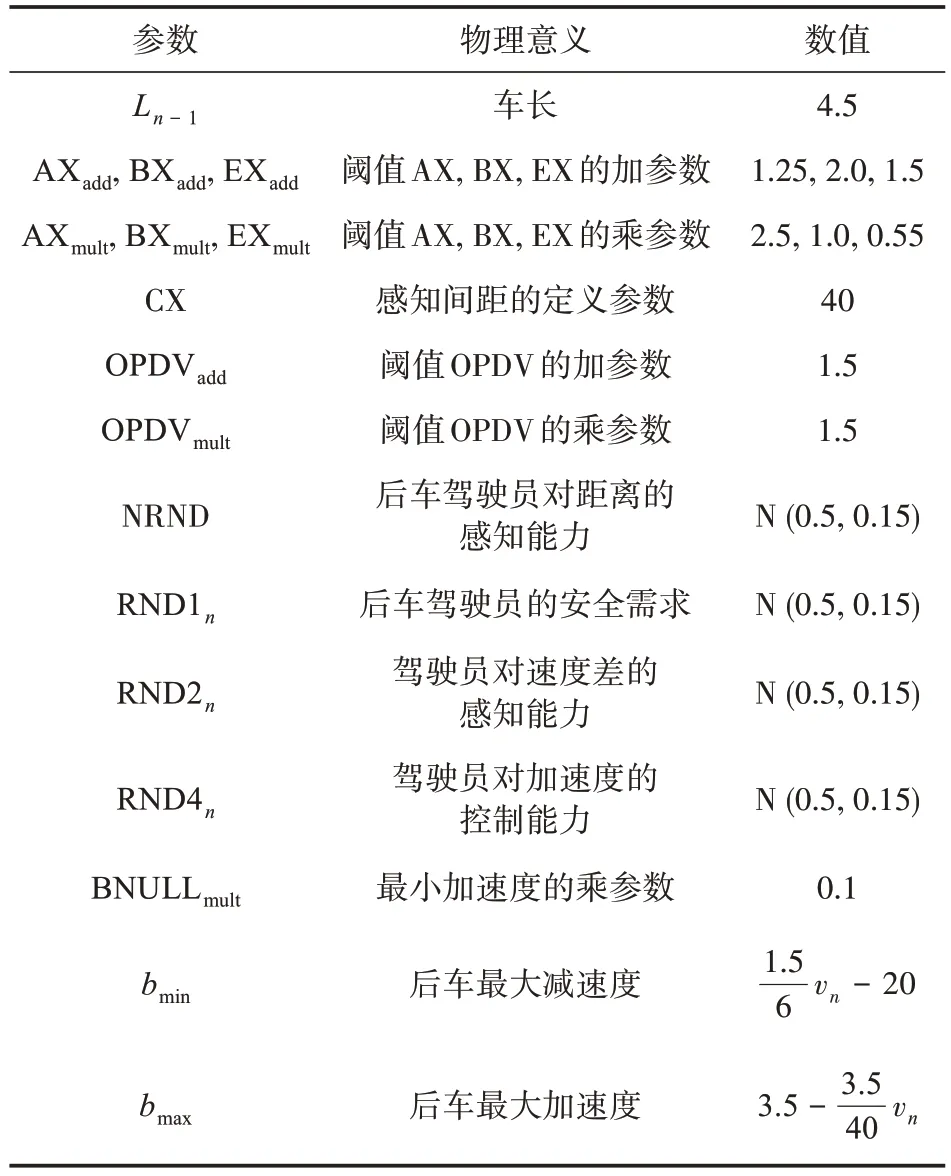
表1 Wiedemann模型数值仿真参数设置

Wiedemann 跟驰模型各跟驰域所采用的加速度相互独立，各跟驰域边界及对应的驾驶行为如表2所示。各加速度模型如式（2）～式（4）所示。

表2 Wiedemann跟驰域边界及加速度模型

表2 （续）

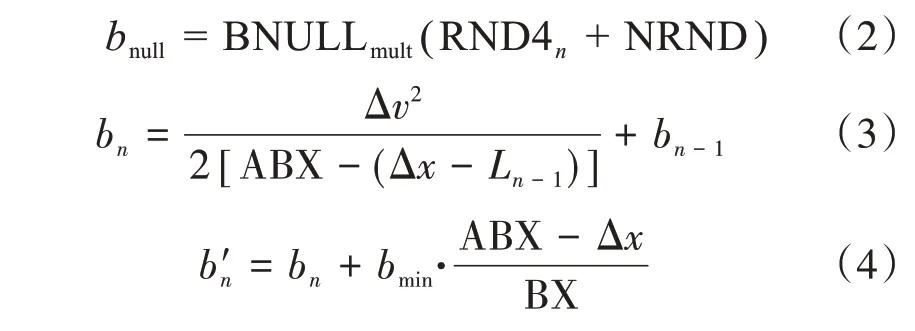
式（2）～式（4）中：bnull为无意识加速度（m/s2）；BNULLmult为待标定参数；bn为紧急制动跟驰域下的减速度（m/s2）；Δv为当前时刻速度差（后车速度减前车速度）（m/s）；ABX 为速度差较小时，前后车期望最小跟驰车头间距（m）；Δx为前车与后车的间距（m）；Ln-1为前车车长（m）；bn-1为前车的加速度（m/s2）；为接近前车跟驰域下的减速度（m/s2）；bmin为后车最小加速度（m/s2）；BX为两车安全间距（m）。

2.3 jerk分布特征

急动度（jerk）是描述加速度变化快慢的物理量，单位为m/s3，其物理意义为驾驶员踩油门速度的快慢，计算公式如式（5）所示。

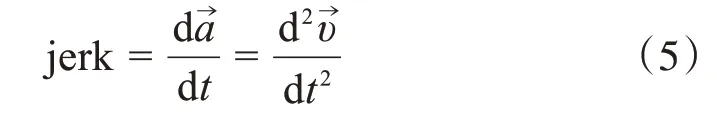
以99.5%和0.5%分位数为上下限，分析速度、加速度与jerk的关系。速度-加速度区间下对应的jerk均值分布如图4所示。

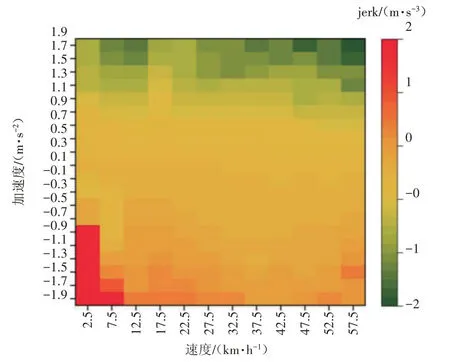
图4 速度-加速度对应jerk均值分布

从图4 可以看出，jerk 均值与速度的相关性较小，而与加速度的相关性较大。jerk 均值与加速度呈负相关关系，这表明jerk 能够让加速度尽可能维持在0m/s2左右变化，这与实际驾驶过程中驾驶员稳定行驶车辆的特征相符。

对各加速度区间下jerk 分布特征进行拟合分析，可以发现，不同加速度区间下jerk 服从高斯分布，且拟合度R2皆在0.9 以上。加速度为负值和正值时jerk的分布情况如图5所示。

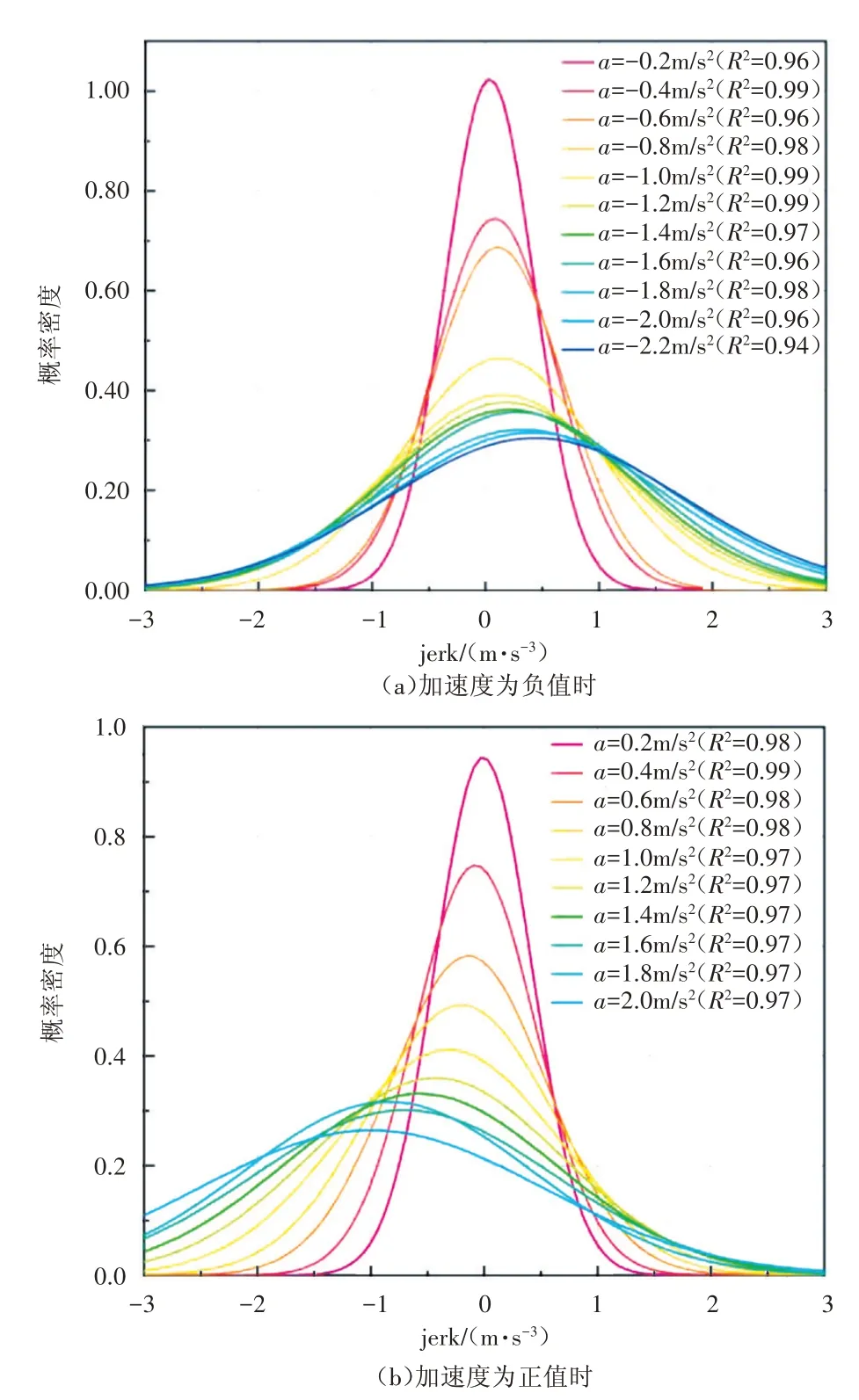
图5 各加速度区间下jerk分布

从图5 可以看出，当加速度为负值时，随着加速度减小，jerk 逐渐向右偏移，分布逐渐分散；当加速度为正值时，随着加速度增大，jerk分布逐渐向左偏移，分布也逐渐分散。这表示在驾驶过程中，车辆速度变化幅度增大时，jerk 变化幅度也会增大，进而维持车辆稳定行驶。

基于车辆跟驰数据进一步分析jerk 边界值及分布规律，不同加速度区间下对应的jerk 最大值与最小值分布如图6所示。

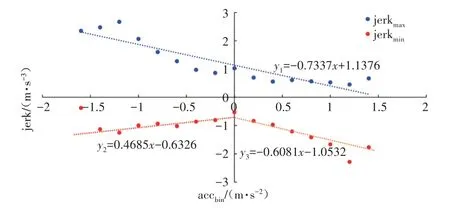
图6 各加速度区间下jerk边界值及拟合关系

由图6 可以看出，jerk 最大值随着加速度增大而逐渐减小；当加速度小于0 时，jerk 最小值随加速度增大而增大；当加速度大于0 时，jerk最小值随加速度增大而减小。利用线性函数拟合加速度与jerk 的关系，表达式如式（6）、式（7）所示，拟合度R2皆大于0.8。模型优化时，基于加速度区间和jerk 边界值拟合公式即可求得相应的jerk边界值。

式（6）～式（7）中：jerkmax为jerk最大值（m/s3）；jerkmin为jerk 最小值（m/s3）；accbin为加速度区间（m/s2）。

以1m/s的粒度划分速度差，以0.2m/s2的粒度划分后车加速度，不同速度差-后车加速度区间下对应的加速度均值如图7所示。

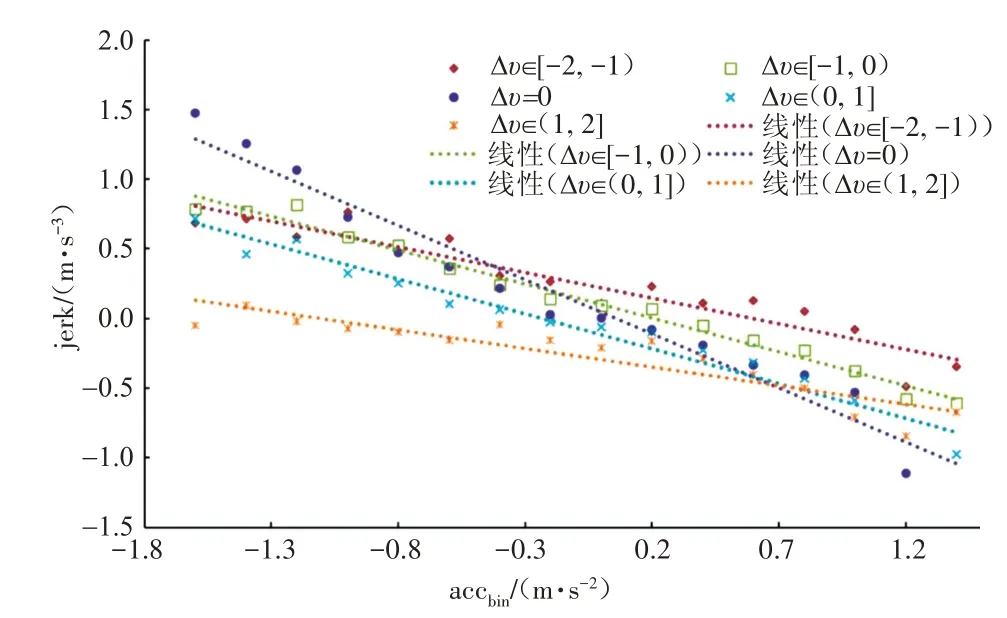
图7 速度差-加速度区间jerk均值拟合

不同速度差区间下，jerk 的均值皆与加速度呈线性相关，且拟合度较高。假设各速度差-后车加速度区间下对应的jerk 分布服从高斯分布，则jerk 拟合关系式如式（8）～式（10）所示。拟合后，各速度差区间下jerk 分布的标定参数a,b值及方差如表3所示。

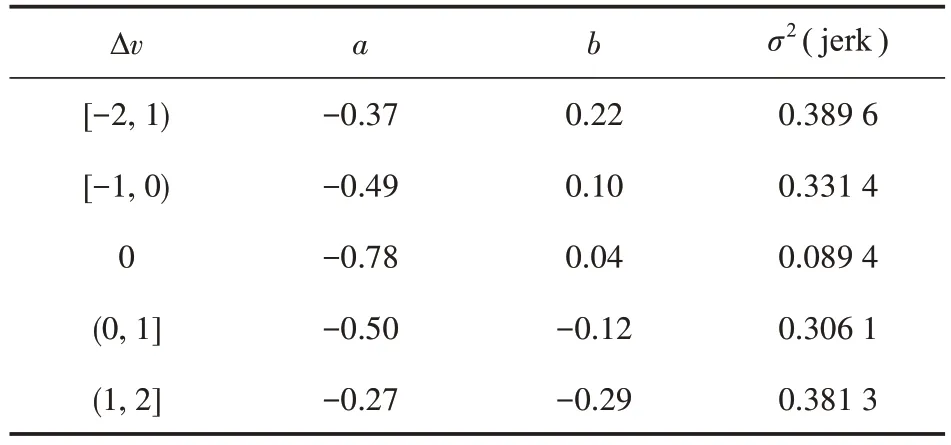
表3 jerk标定参数及方差

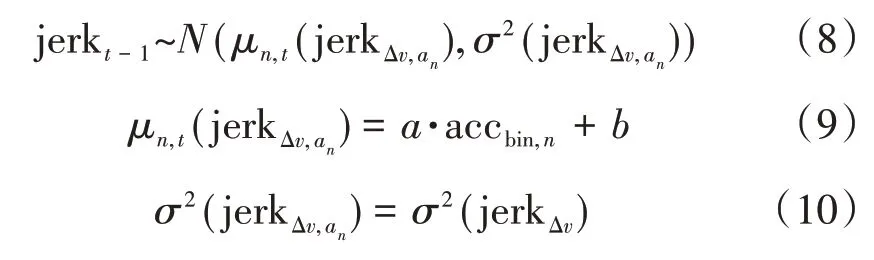
式（8）～式（10）中：μn,t(jerkΔv,an)为后车当前时刻速度差-后车加速度区间下对应的jerk 期望值。σ2(jerkΔv,an)为速度差-后车加速度区间下jerk 的方差；accbin,n为后车前一时刻对应的加速度区间；σ2(jerkΔv,an)为速度差∆v区间下对应jerk 的方差；a和b为待标定参数。

综上，实际行驶过程中，jerk 是影响加速度变化和车辆行驶稳定性的重要参数，与加速度呈负相关关系，且各加速度区间下jerk 服从高斯分布。由于Wiedemann 模型不具备刻画实际轨迹中jerk 分布特征的能力，使得其输出轨迹存在不真实的加速度。因此，若能提高跟驰模型jerk 的刻画能力，则可提高模型输出轨迹的准确性。

2.4 模型优化方法

基于实际轨迹中jerk分布规律，提出考虑jerk分布的Wiedemann 跟驰模型优化方法，在跟驰模型中增设jerk 约束，使该仿真模型生成连续而非“跃迁”式变化的加速度，从而提高其排放测算精度。Wiedemann跟驰模型优化算法如图8所示。

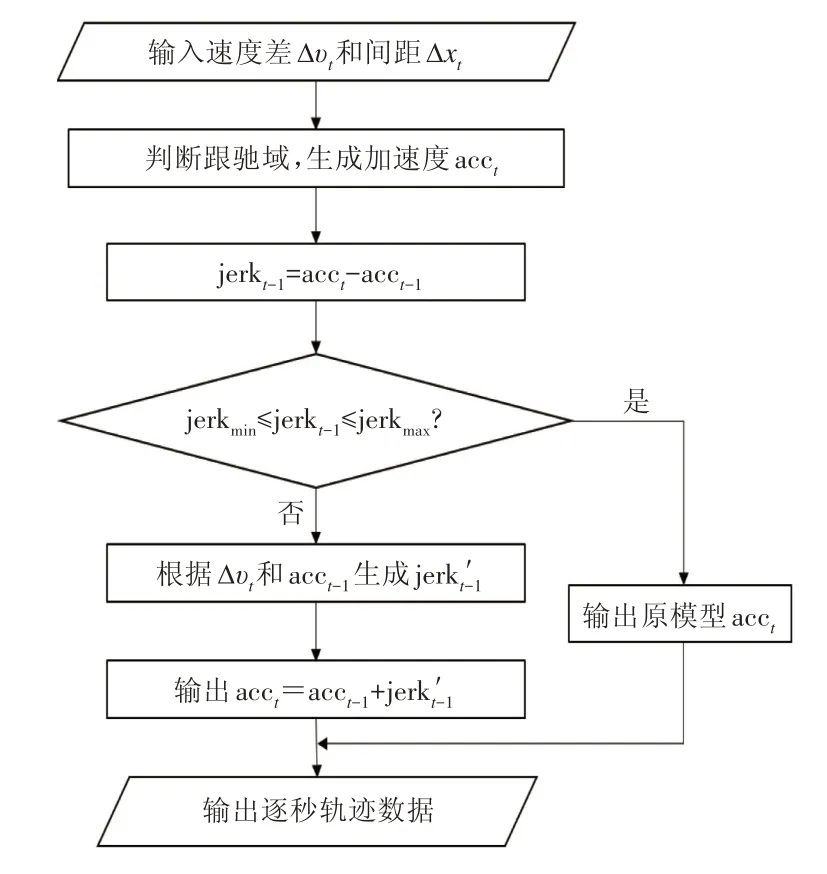
图8 考虑jerk分布的Wiedemann跟驰模型优化流程

首先，模型根据t时刻前后车间距（Δx）与速度差（Δv）判断跟驰域，基于跟驰域生成后车t时刻的加速度acct，此步骤与原模型一致。

其次，根据t和t-1 时刻的加速度，计算t-1时刻的jerkt-1。

再次，判断jerkt-1是否在[jerkmin,jerkmax]区间内。若jerkt-1不在此区间内，则模型根据当前速度差和t-1 时刻的acct-1生成一个新的jerk't-1，随后再基于jerk't-1生成t时刻acc't；若jerkt-1在此区间内，则保留原模型生成的acct。为了防止前后车相撞，本优化模型采用RPA 跟驰模型中的安全距离子模型[20]对后车进行约束，仿真加速度an如式（11）所示：

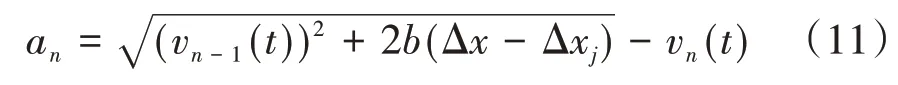
式（11）中：vn-1(t),vn(t)分别为t时刻前车与后车的速度（m/s）；b为后车最大减速度（m/s2）；Δxj为最小车头间距（m）。

最后，根据模型生成的加速度再输出逐秒轨迹数据进行排放测算。

同时，为了保证模型仿真的稳定性，该优化模型还增设了如下两个边界条件：①当后车速度远大于前车且车辆间距较小时，后车应采取减速措施，故模型生成的jerk为负值，设置临界次数，若超出临界次数未生成负值，则输出生成所有jerk 中的最小值；②当后车速度远小于前车且车辆间距较大时，后车应采取加速措施，故模型生成的jerk 为正值，设置临界次数，若超出临界次数未生成正值，则输出生成所有jerk中的最大值。

3 应用案例

3.1 对比指标选取

采用相对均方误差（Relative Mean Square Error,RMSE）作为jerk 区间、VSP 区间分布对比指标，采用相对误差（Mean Absolute Percentage Error,MAPE）作为排放因子测算效果的对比指标。误差越大，表明仿真行驶轨迹与实际轨迹相差越大，反之越小。Jerk 区间分布、VSP 区间分布相对均方误差RMSEi及排放因子相对误差MAPEEF的计算公式如式（12）、式（13）所示。

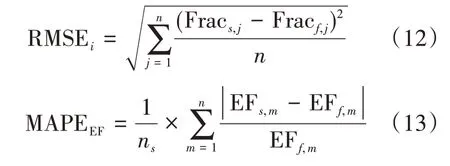
式（12）～式（13）中：Fracs,j为仿真输出的jerk/VSP 区间j分布值；Fracf,j为实际轨迹的jerk/VSP区间j分布值；n为区间数；EFs,m为仿真输出在速度区间m的排放因子；EFf,m为实际轨迹在速度区间m的排放因子。

3.2 交通轨迹优化效果分析

以北京市出租车轨迹数据作为优化仿真模型输入的前车数据，验证本文提出的考虑jerk 分布的Wiedemann 跟驰模型优化方法的有效性。从优化后模型输出轨迹中随机选取一段观察轨迹速度变化情况，如图9 所示。可以看出，考虑jerk 约束后，原模型中急减速、急加速的不真实驾驶行为有明显改善；优化后，后车速度变化趋于平稳且更接近前车。

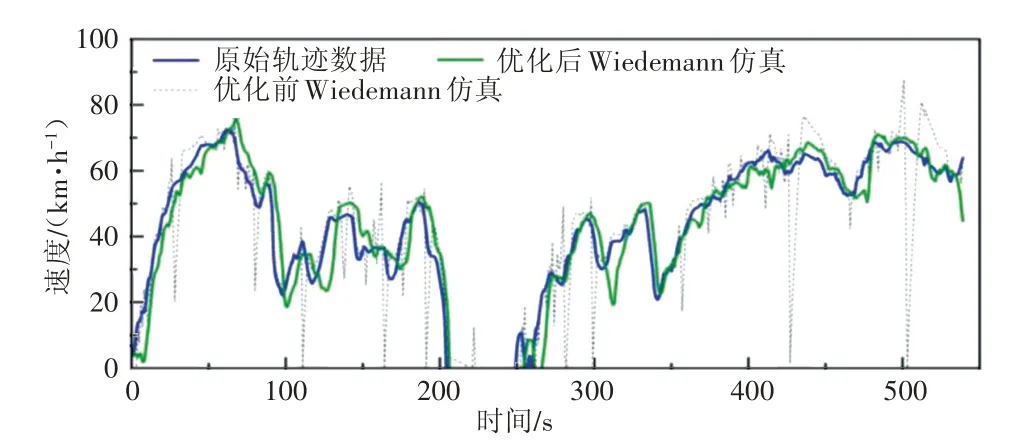
图9 Wiedemann模型优化前后轨迹速度

优化前后Wiedemann 输出轨迹的瞬时加速度变化如图10所示。可以看出，原Wiedemann 模型中呈“跃迁”式变化的加速度有明显改善，优化后加速度变化皆在合理的范围内连续变化。

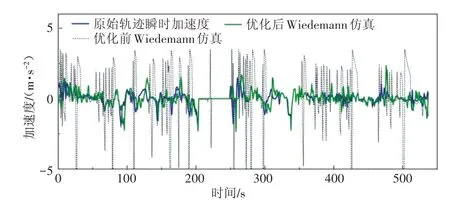
图10 Wiedemann模型优化前后轨迹瞬时加速度

原始轨迹及优化前后仿真轨迹的jerk 分布如图11所示。可以看出，原模型中两端不真实的高jerk 分布值有明显降低，优化后的jerk 分布值会更接近实际分布，jerk 仿真与实际分布的相对均方误差由4.6%降低至1.4%。

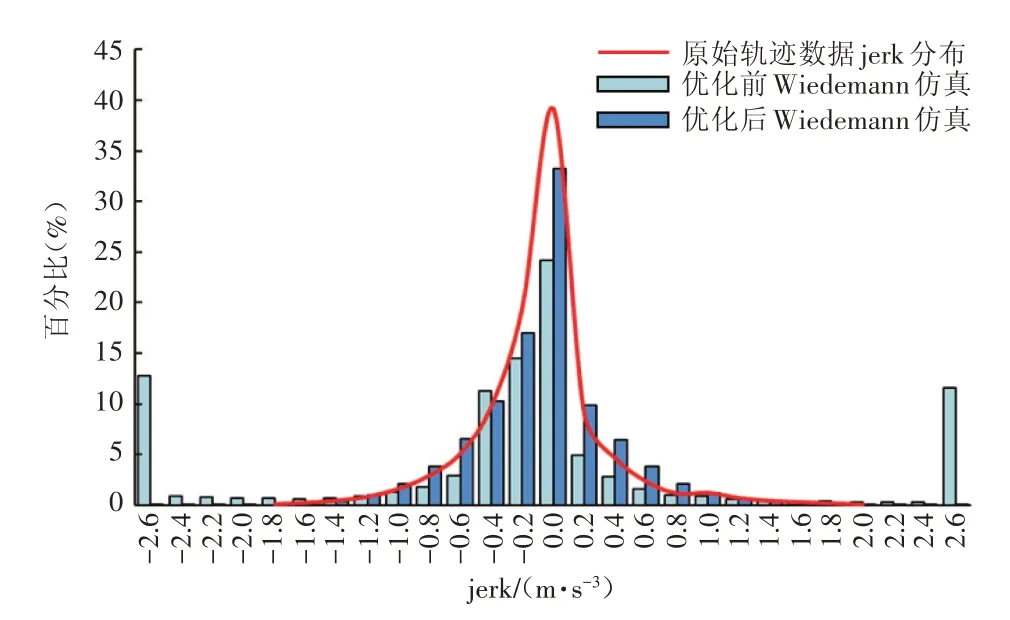
图11 Wiedemann模型优化前后轨迹jerk分布

3.3 面向排放测算的优化效果分析

相比于Wiedemann 跟驰模型，增设jerk 约束的Wiedemann 优化模型生成轨迹的VSP 分布形态与实际分布更为接近，原模型中不真实的剧烈做功也得到明显改善。优化前后的Wiedemann 跟驰模型VSP 相对均方误差对比图如12 所示。可以看出，经jerk 约束后，各速度区间下VSP 相对均方误差皆有明显的降低，平均每个速度区间误差下降了1.2%。

排放因子指机动车行驶单位距离所排放污染物的质量。本文选用排放因子作为跟驰模型排放测算的对比指标，基于VSP 和排放率可以计算出各平均速度区间下CO2,CO,THC 和NOx 的排放因子。排放因子计算公式如式（14）所示，平均排放率选择轻型汽车的排放数据来计算[21]。

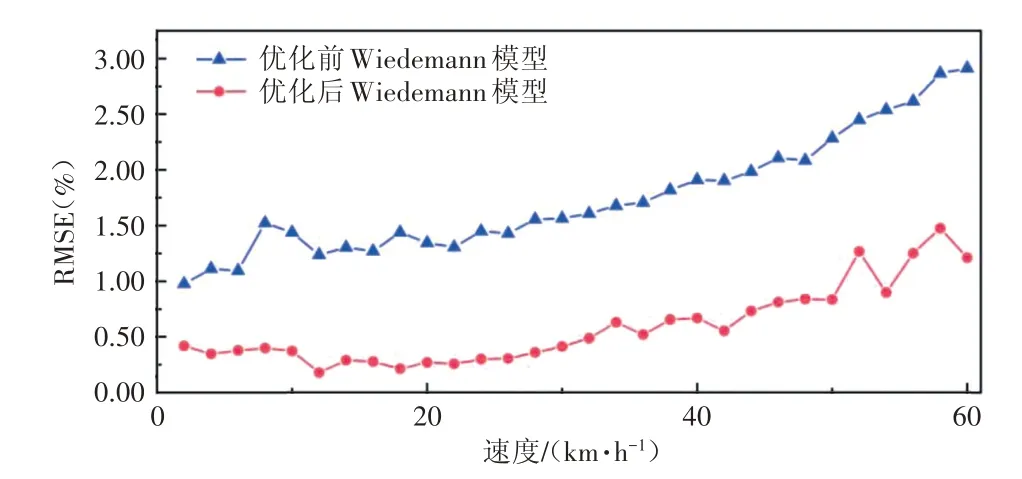
图12 Wiedemann模型优化前后输出轨迹VSP均方误差

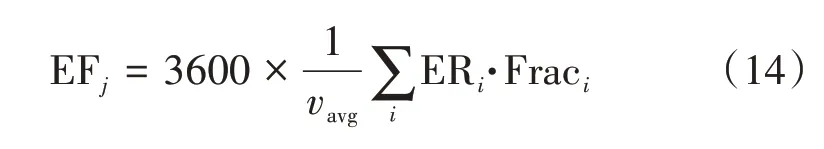
式（14）中：EFj为平均速度区间j的排放因子（g/km）；vavg为该平均速度区间的平均速度（km/h）；ERi为VSP 区间i的平均排放率；Fraci为第i个VSP区间的分布值。

优化前后Wiedemann 仿真模型与实际轨迹的CO2,CO,THC,NOX排放因子对比如图13所示。从排放因子对比可以看出，考虑jerk 约束的Wiede⁃mann 优化跟驰模型排放因子更接近原始轨迹数据，该优化方法能够有效降低排放测算的误差，经计算优化后CO2,CO,THC,NOx的排放因子平均误差较Wiedemann 模型分别下降16.9%,118.3%,27.0%,20.5%。

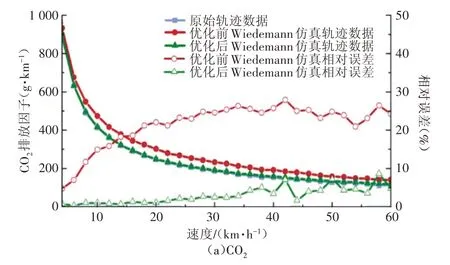
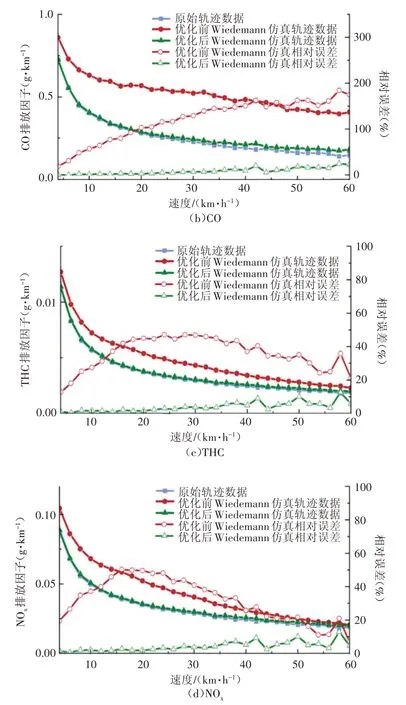
图13 Wiedemann模型优化前后输出轨迹与实际轨迹数据（4种排放物排放因子）

3.4 模型优化评价

由案例分析可知，本文所建立的面向排放测算的跟驰模型优化方法能够有效提高输出轨迹的稳定性及排放测算精度，模型的创新点及优势归纳如表4所示。

表4 优化前后Wiedemann跟驰模型对比

表4 （续）

4 结语

跟驰模型输出轨迹的排放测算误差主要来自其不真实的加速度，而jerk 是影响加速度变化的重要参数。本文基于实际轨迹数据量化分析jerk分布规律，结果表明jerk 与加速度相关性较大且呈负相关关系，每个加速度区间下jerk 服从高斯分布。而Wiedemann 仿真模型不具备刻画实际轨迹中jerk 分布特征的能力，因此可通过提高模型jerk刻画能力，提升输出轨迹的准确性。

本文提出在模型中增设jerk 约束的方法实现Wiedemann 仿真跟驰模型的优化。优化后Wiede⁃mann跟驰模型的稳定性和排放测算精度有明显提升，其生成的轨迹会更加平稳且与前车轨迹接近，在每个平均速度区间下，仿真生成轨迹所建立的VSP 分布误差平均下降了1.2%。CO2,CO,THC,NOx 的排放因子测算平均误差较Wiedemann模型优化之前分别下降16.9%,118.3%,27.0%,20.5%。

面向排放测算的跟驰模型优化方法准确刻画了车辆在实际跟驰状态下加速度变化情况，提高了微观交通仿真模型与基于VSP 分布的排放模型融合测算交通排放的准确性。未来将研究不同道路类型下，该模型优化方法对提升排放测算精度的有效性，并将优化模型进一步应用于辅助驾驶或网联驾驶场景中，以规范车辆驾驶行为，保证车流行驶稳定性从而引导车辆降低排放。