基于桩土耦合的系泊锚桩水平承载力有限元分析

刘生法

（广州船舶及海洋工程设计研究院，广州 510250）

1 概述

海洋工程浅水系泊系统，往往采用钢管桩进行海底锚固。钢管桩自重较轻，结构形式简单，施工较为简单，工程可靠性较高；近几年来，海上风电场建设的发展迅猛，其基础也大量采用钢管桩的固定方式，并且管桩直径逐渐增大，入土深度也不断加深。

对于系泊系统而言，锚桩主要承受水平载荷，准确地计算管桩的水平承载能力显得尤为重要。传统的锚桩水平承载力计算方法，主要有以下几种：

（1）极限地基反力法[1][2]:如恩格尔法、斯奈特科法、雷斯法等，其地基反力的分布形状（直线或抛物线）是事先假定的，地基反力只是桩入土深度的函数，与桩的挠度没有直接关系，此法多用于短桩；

（2）弹性地基反力法：包括线性弹性地基反力法、非线性弹性地基反力法等，主要适用于桩侧土体处于弹性变形阶段的求解，其计算结果往往和实际情况有一定差距；

（3）复合地基反力法：如P-y 曲线法[1][2][3]，能够真实地反应桩周土的非线性特性及桩的内力和变形特性，可用于桩基大变形非线性分析，被认为是分析桩土水平非线性变形最有效的方法，但其结果偏于保守且主要适用于管桩直径较小的情况。

随着计算机技术的发展，有限元法被越来越多地应用于桩土相互作用分析中，其可以适应不同直径和不同材料的管桩以及不同的海底土质，具有较高的计算精度。

2 设计输入参数

本文案例为“湛江舰”退役安置系泊工程项目，最高需抵抗17 级台风。初步方案采用4 点悬链式配重系泊，海底采用大直径钢管桩进行锚固，生存工况下最大系泊载荷约500 t，根据API[4]系泊定位规范，取安全系数1.6，锚桩应能承受800 t 的水平荷载；管桩直径初步取为3 m、壁厚取为50 mm、桩长取为35 m。

根据工程地质勘查和土工试验报告，获得其中一个桩位（相对比较薄弱）各土层力学指标数据，见表1。

表1 锚桩土层数据表

3 物理建模

3.1 桩土几何模型

钢管桩为圆柱形，按直径3 m、壁厚50 mm、桩长35 m 进行建模。在前期的试算中，发现载荷作用位置附近应力很大，远超出材料屈服极限，所以对载荷作用位置附近的管桩眼板和钢管做了结构增强，其中眼板部分厚度100 mm、桩顶垂向筋板高2 m、板厚100 mm。

为方便土体建模，土体几何模型取为圆柱体；为使模拟能够更加接近桩土效应的实际情况，避免模型边界条件对数值模拟结果的影响，土模型圆柱直径取桩径20 倍、土模型深度取桩长2 倍；考虑到水平受荷桩关于X 轴的对称性，为简化起见，锚桩模型和土层模型均取一半进行分析，因此整个土体模型设置为直径60 m、深度70 m；由于暂不考虑打桩过程，土体建模时预留了与管桩直径相同的孔。图1 为桩土几何模型图。

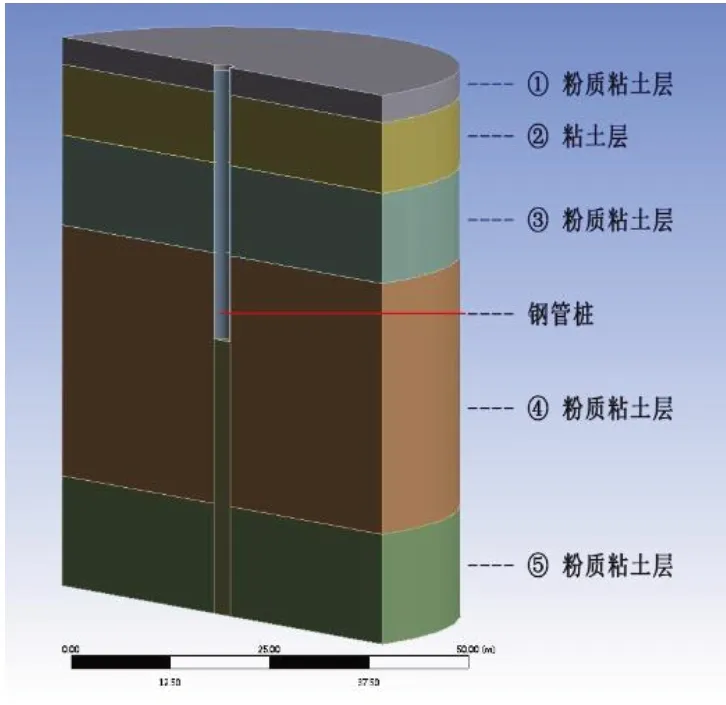
图1 桩土几何模型

3.2 土体本构模型

（1） Mohr-Coulomb 和Drucker-Prager(D-P) 系 列屈服准则

在土体的力学分析中，常采用Mohr-Coulomb 本构模型和Drucker-Prager 本构模型。由于Mohr-Coulomb屈服准则在三维主应力空间中的屈服面存在6 条求导不连续的角棱线（见图2），故Drucker-Prager 模型对M-C 模型的屈服面函数作了适当的修改，采用圆锥形屈服面来代替Mohr-Coulomb 六棱锥屈服面，从而改善了数值计算的收敛性。

图2 MC 和DP 系列屈服准则在π 平面上的屈服曲线

M-C 准则认为材料的破坏属于在正应力作用下的剪切破坏，土体将沿着剪应力和正应力最不利组合的某一面发生破坏，其表达式为：

|τ| =c+σtanφ（1）式中：c为土体粘聚力；σ 为正应力；φ土体内摩擦角。由此可以推导出：

（2）式中：θσ为罗德角；J2为偏应力张量第二不变量，J2=（σ1-σ2）2+（σ2-σ3）2+（σ1-σ3）2；I1为 主应力张量，I1=σ1+σ2+σ3。

Drucker-Prager 于 1952 年在 Mises 强度条件的基础上，提出了广义Mises 屈服与破坏准则，即在主应力空间中，D-P 屈服面服从以下表达式：

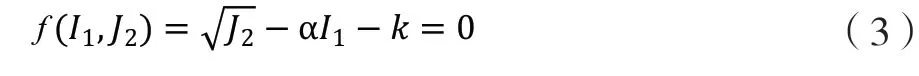
式中：f 为塑性势函数；α、k 为材料常数。

通过式（2）和（3）可以得出不同受力条件（即不同的 θσ）下的 α、k 值。通常将式（3）称为 DP 系列屈服准则，在 π 平面上其屈服曲线为一组圆（见图2），共有5 种与M-C 条件相关的α、k 值，相对应的有5 个圆准则： M-C 外角点外接圆准则（DP1）；M-C 内角点外接圆准则（DP2）；M-C 内切圆准则（平面应变关联法则下 M-C 条件，DP3）；M-C 等面积圆准则（DP4）； M-C 匹配D-P 圆（DP5）。本文暂不考虑DP4 和DP5 的情况，见表2。

表2 Drucker-Prager 系列屈服准则之α、k 参数表格

（2）DP2 等效

研究表明：上述DP1 模型在评价地基承载力时，会得出较大的安全系数，是偏于不安全的；DP3 模型在评价地基承载力时，会得出较小的安全系数，是偏于保守的；而DP2 模型在评价地基承载力时，会得出较适中的安全系数，是比较安全的。本文以DP2 模型进行分析评估。

在ANSYS 中缺省使用DP1 屈服准则，当采用DP2屈服准则时，必须作一个等效转换，设转换后新的参数为αt、kt、φt、ct，并令αt=αDP2、kt=kDP2，则有

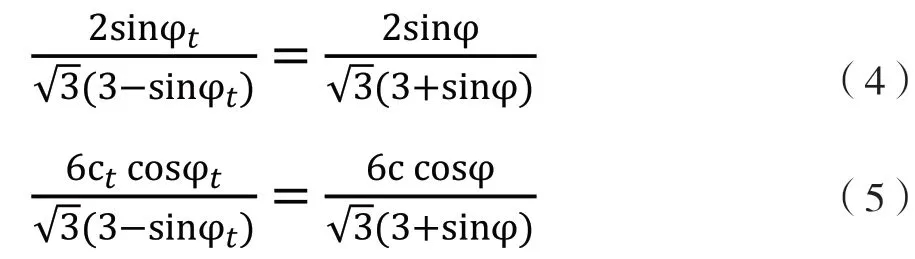
根据式即（4）（5），可解出φt、ct，见表3。

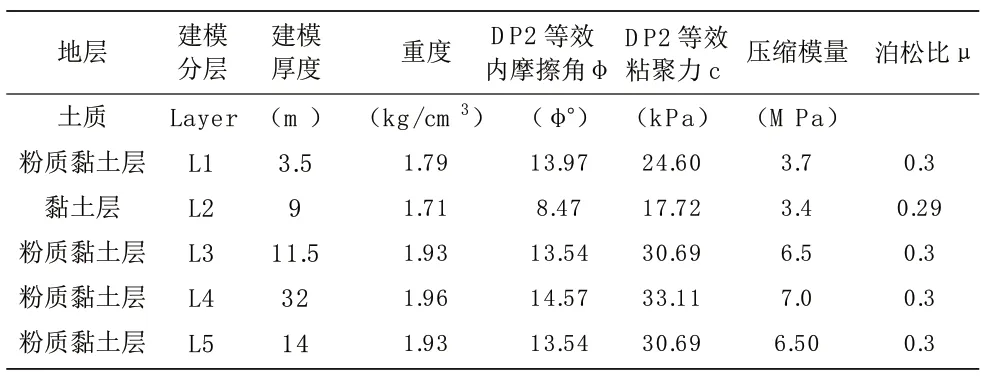
表3 DP2 等效锚桩土层数据表

3.3 桩土有限元模型

所选用的锚桩为钢管桩，其基本尺寸为高度35 m、管径3 m、壁厚50 mm。为了便于计算，利用其对称性选取整体模型的1/2 进行计算。土体分为5 层，建模厚度见表2；有限元网格划分为75 244 各单元，其中实体单元54 240 个、接触单元20 812 个。

根据系泊力计算结果，设计水平承载力需要800 t，在桩顶施加800 t 水平载荷，考虑半个整体模型，实际计算施加400 t 水平载荷；桩体选用碳素结构钢，系链眼板及加强部分采用船用结构钢，其弹性模量E=210 GPa、泊松比μ=0.3。

建模要点如下，有限元模型见图3。

图3 桩土有限元模型

（1）土体模型采用包围管桩的圆柱体，有利于减少单元数量；

（2）管桩孔建模一直延伸到模型底部，管桩底部采用与管径相同的一段土柱，有利于网格划分的规整，对计算结果基本没有影响；

（3）整个模型尽可能全部采用六面体单元（对应ANSYS186 单元），可以显著加快求解速度；

（4）管桩与土体之间采用摩擦接触，管桩底部与土柱之间采用无摩擦接触，土层之间采用绑定接触；

（5）模型底面采用固定约束，模型外侧面采用水平位移约束，模型对称面（包括管桩、眼板和垂向筋板）采用法向位移约束；

（6）桩顶水平载荷按照轴承载荷的形式施加在眼板内孔曲面上，相当于非均匀分布的正弦载荷，有利于避免载荷施加位置局部应力集中；

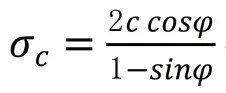
4 分析设置与计算结果

分析设置中开启自动时步，设置足够大的子步数（如1 000 000）；开启弱弹簧，以防止产生刚体位移；开启大挠度选项，以适应几何非线性；适当放宽收敛容差（如力的容差由0.5%放到1%，位移容差由0.5%放到2%），以加快收敛速度，基本不影响工程精度。

Ansys 提供多个分析求解器选项，如SPARSE 直接求解器、PCG 预条件求解器、JCG 雅科比共轭梯度求解器和ICCG 非完全共轭梯度求解器等。建议尽可能选用SPARSE 直接求解器，当然相应地需要有较大的内存（建议不小于48 GB）并配合固态硬盘，同时开启8核以上并行计算，可以大大缩短解算时间。

（1）管桩应力

管桩等效应力计算结果，见图4，桩身等效应力见图5。

图4 管桩（含眼板及加强部分）等效应力云图

图5 桩身局部等效应力云图

由图4 可知，含眼板和加强部分时，管桩最大等效应力343 MPa，发生在管桩板眼处，桩身最大等效应力233 MPa，发生在桩身中部。

（2）管桩水平位移

桩身顶部最大水平位移0.412 m（处于一般规定的允许水平位移范围）[2]，桩身底部水平位移－0.081 m，零位移发生在泥面下25.44 m 处。管桩定向变形图，见图6。

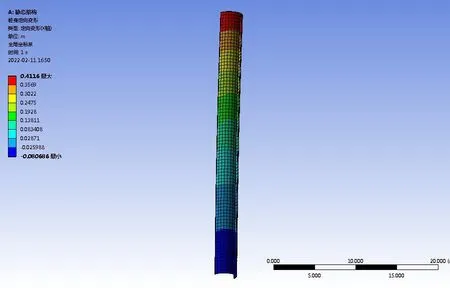
图6 桩身定向变形云图

5 结语

根据上述分析结果：桩身部分可选用碳素结构钢Q275，其屈服应力ReH=255 MPa、最大等效应力233 MPa＜ReH，满足规范要求；眼板和加强部分可选用船用结构钢AH36，其屈服应力σs=355 MPa、ReH=355 MPa，最大等效应力343 MPa＜ReH,，满足规范要求。

实际计算时，为了确定合适的管桩材料和结构型式并满足规范要求，上述管桩直径、壁厚、眼板厚度以及垂向筋板尺寸，均需要在给出设计初值后进行一系列的优化计算，才能获得合理可行的设计结果。

三维有限元法求解桩土耦合力学问题，可以同时考虑土壤的材料非线性、管桩的大变形以及桩土接触的状态非线性，已被大量的实践和试验证实其准确性。本案例由于水平载荷非常大，直接在海上进行拉力试验验证非常困难，所以一般可以通过第三方或通过不同人员不同仿真软件进行计算验证，而上述基于桩土耦合的系泊锚桩水平承载力有限元分析方法，已被较多的应用在实际工程的设计分析中。