基于BP神经网络的降水量估算模型在自动气象站降水量质量控制中的应用

年飞翔， 郭 阳， 徐 梅， 黄纯玺， 金 津， 黄文婷， 梁 健， 王 艺

(1.天津市气象信息中心，天津 300000； 2.重庆市气象科学研究所，重庆 400000)

引 言

自动气象站作为地面观测设备中站网密度最高的观测设备，其观测数据已被广泛应用于气象业务和科研中，尤其自动气象站降水资料在预报验证、决策预警、农业服务等方面发挥了重要作用。自动雨量计是自动气象站中的降水观测设备，与气温、气压等观测设备相比，其更容易受到观测环境的影响，造成观测误差。例如异物堵塞造成降水量偏小和滞后，园林灌溉造成无效降水，某侧建筑物遮挡造成该侧风向时降水偏小。同时，区域自动气象站往往由于维护、检定不及时造成观测设备存在系统性偏差[1]。因此，为保证自动气象站降水资料在应用中的准确性，对其质量控制十分必要。

在地面气象观测资料质量控制工作中，降水由于局地性强、非连续性的特点，难以通过时间一致性、内部一致性检查等方法检测出错误数据，气候界限值检查只能发现异常偏大的降水量[2-4]。空间一致性检查是降水质控中最为有效的方法。该方法利用空间插值法、空间回归法、气候统计比较法等算法建立函数模型，通过对比模型估算值和实测值差异，实现降水质控[5-6]。任芝花等[7]利用降水的界限值及时空一致性，对全国区域自动气象站和国家级自动气象站实时上传的逐小时降水资料进行了质量控制。王海军等[8]在自动气象站实时资料自动质量控制研究中，应用了基于空间插值算法的空间一致性检查。姜明等[9]采用反距离加权法，对天津区域自动气象站小时降水量进行空间插值检验。空间线性回归法在湖北省自动气象站逐时降水量资料质量控制中取得了较好的质控效果。但是，对流性降水由于突发性强、空间尺度小，不仅在中短期预报中难以准确预报[10]，上述研究中使用的单一线性或非线性函数也难以准确描述其空间变化规律，同时复杂的参数计算也给应用带来不便。

在气象资料质量控制工作中，部分无法被现业务运行的自动质量控制系统检测出的疑误降水数据，通过人工与周围站点数据对比，可轻易识别出异常。人工判别过程得益于人脑可以对数据信息进行复杂抽象的思考和处理，可根据经验对数据质量快速准确作出判断。人工神经网络是一种模仿人脑神经系统结构和处理信息方式的智能运算模型，它由许多节点(神经元)相互联接，可以通过大量样本的训练获得处理数据的“经验”，并根据“经验”对新数据作出判断[11-14]。目前人工神经网络在多个行业和领域均有应用，如油菜花期预测、股票价格预测等[15-19],以及在气象上的模式预报释用、雾霾预测等[20-23]。如果人工神经网络能够应用于自动气象站降水数据质量控制，可以有效提高数据质控效率，降低人工成本。为此本文构建BP神经网络，探讨该方法在自动气象站降水数据质量控制中的适用性。

1 数据与方法

1.1 数据收集与处理

利用天津市内自动气象站逐小时降水量观测数据开展研究，降水数据均经过质量控制。自动气象站分布于天津各行政区，降水量数据具有代表性。

模型使用各站降水量大于0 mm的数据作为神经网络训练目标值。使用距离待检站点最近的10个自动气象站作为邻近站，将各站按与待检站的距离从小到大排序，并依此序将邻近站待检时次小时降水量、邻近站与待检站距离共20个要素作为神经网络训练的输入值。使用2019年4月1日至2019年8月15日各站降水量数据构建样本数为41413个的训练样本，用作模型结构、参数优化和预训练。使用2018年4至10月各站降水量数据,作为应用模型的再训练、检验和预测样本。

为了满足神经网络模型训练需求，便于不同单位或量级指标的比较和加权，采用公式(1)对样本进行归一化处理，并对表达式无量纲化：

(1)

1.2 神经网络模型设计

1.2.1 神经网络结构

Robert Hecht Nielson等的研究表明，一个隐含层的神经网络就可以模拟出任意n维到m维的连续函数。研究认为，增加隐层数可以降低网络误差、提高精度，但复杂网络会增加训练时间，同时可能出现“过拟合”的问题[24-26]。因此，本文选用三层的结构构建神经网络模型，既输入层、隐含层、输出层。在BP网络中，隐含层节点数不仅会影响神经网络模型的性能，而且决定着训练时是否会出现“过拟合”。

s=log2n

(2)

(3)

(4)

(5)

式中，s为隐含层节点数，n为输入层节点数，l为输出层节点数，a为常数。

上述4种方法均针对训练样本任意多的情况，一般某一种公式很难适用于各种情况。因此本文采用上述4种经验公式确定隐含层节点数的区间，然后使用试凑法对区间内每个节点数构建网络，并寻找出误差值最小的网络，对应节点数即为最优节点数。

1.2.2 训练函数选择

常用的神经网络训练方法有弹性梯度下降法、Levenberg-Marquardt法(LM)、自适应lr动量梯度下降法、量化共轨梯度法、一步正割法等，其中量化共轨梯度法计算量比其他算法的都小，一步正割法的次之，训练速度较其他方法得更快。LM法所需计算量最大，占用计算资源更多，但是具有收敛速度快的特点。因此，量化共轨梯度法、一步正割法等适合网络结构复杂、数据量较大的大型网络，LM法适用于中小型网络。本文在控制其他训练参数相同的条件下，通过选取不同的训练函数对模型进行训练，并根据训练结果选择最适的训练函数。

1.2.3 模型的检验

利用平方误差(se)和均方误差(mse)表示模型的效果，计算方法如下：

(6)

(7)

2 模型建立与应用

2.1 不同模型超参数的比较

构建隐含层节点数分别为1、5、10至45的三层网络，统一设置训练函数为LM、训练次数为1000、训练目标为0.0001、学习率为0.001进行训练。训练结果(表1)表明，当隐含层节点数为1时，模型经过62次训练后因误差梯度小于10-10而停止训练，模型无法继续收敛。随着隐含层节点数不断增加，模型的均方误差不断减小，模型拟合能力提高。但是，随着隐含层节点数不断增加，增加的节点对模型拟合能力提高的贡献越来越低。同时，较多的隐含层节点数使模型更加复杂，训练速度较慢。因此，在实际使用过程中应根据精度需求和运算能力，设置合适的隐含层节点数。

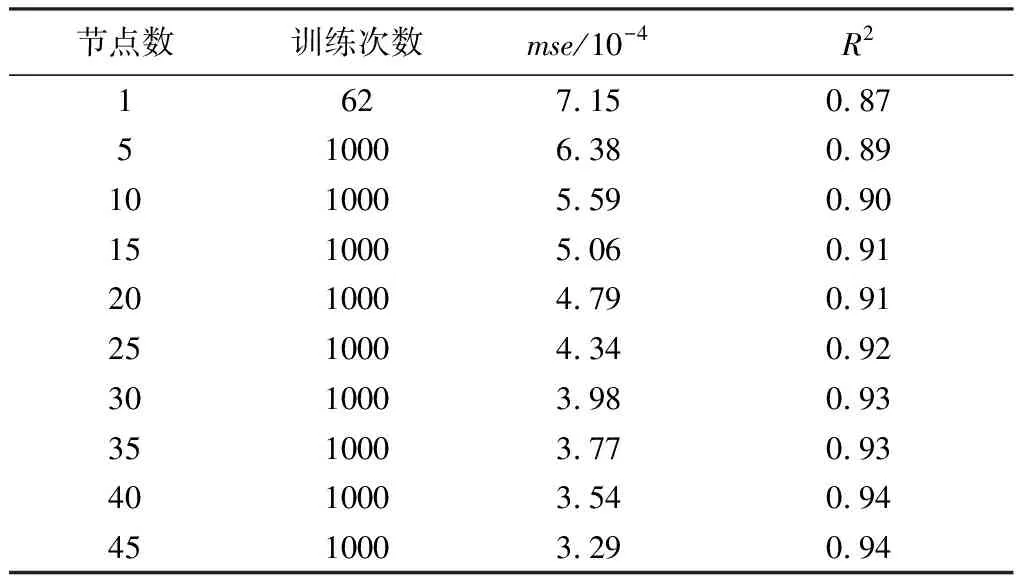
表1 不同隐含层节点数模型训练结果

构建隐含层节点数为25的三层网络，设置训练次数为1000、训练目标为0.0001、学习率为0.001，分别选择5种不同的训练函数对模型进行训练。使用LM作为训练函数模型的收敛速度更快，经过1000次训练模型的误差最小，但所需训练时间最长。使用弹性梯度下降法等其他训练函数，模型迭代速度更快，但收敛速度较慢。因此，本文在之后的研究中均使用LM作为训练函数。

2.2 模型的检验与预测

通过上文的分析并综合计算资源和精度需求，本文选择隐含层节点数为45，训练函数为LM的三层网络模型作为自动气象站小时降水量的估算模型。将2018年4月至10月各站小时降水量数据随机分为70%、15%、15%，分别作为模型的训练(Train)、检验(Validation)、预测(Test)样本，使用原训练1000次后的模型权值作为初始权值继续训练模型。训练过程中使用检验样本对模型进行交叉验证，防止模型过度拟合。使用预训练权值作为初始权值可以大大提高模型的收敛速度，当检验和训练样本的均方误差均达到最小时模型达到最优，此时总样本和三个随机样本输出值与实测值之间的相关系数分别为0.92、0.93、0.90、0.90，模型拟合达到较好的效果(图1)。随着模型继续训练，训练样本的均方误差继续减小，但是检验、测试样本的均方误差开始增大，模型处于过拟合状态。

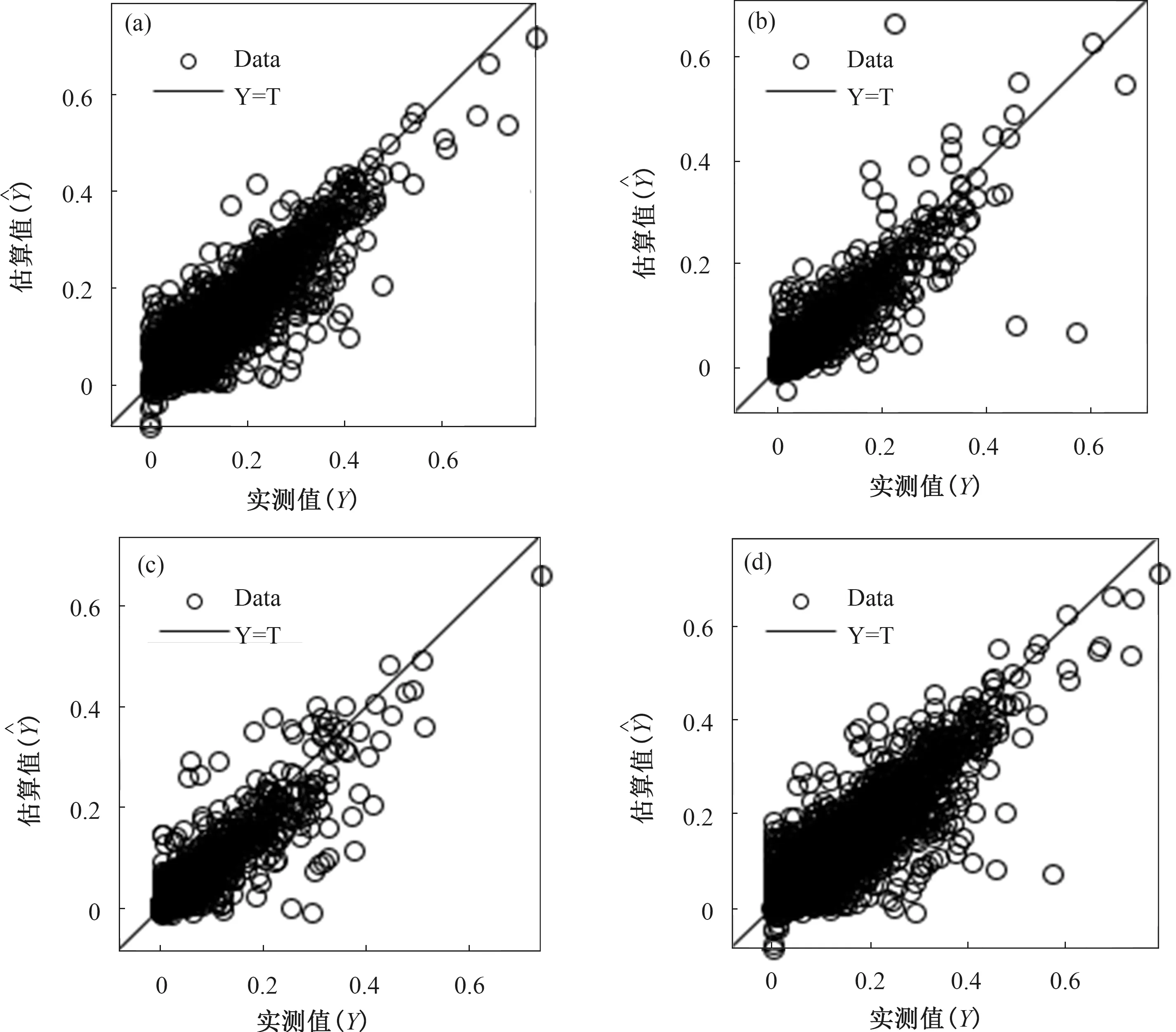
图1 训练(a)、检验(b)、预测(c)、全部(d)样本模型估算值与实测值(归一化值)对比

反距离权重插值是目前自动气象站观测资料空间一致性检查中被广泛应用且效果较好的质控算法。本文利用与输入模型相同的邻近站降水和位置数据，对2018年7月份各站小时降水量数据进行反距离权重插值估算，并与模型估算结果反归一化得到的降水估算值进行对比。结果表明，神经网络模型和反距离权重插值估算结果的均方误差分别为3.80、4.60，神经网络模型估算结果与实测值之间的均方误差更小，较插值法估算结果整体上更优。通过对比单时次估算结果(图2)可以看出，部分时次神经网络模型平方误差远小于反距离权重插值结果，表现出了更好的估算能力。同时，神经网络模型对部分时次的估算误差大于插值估算结果。

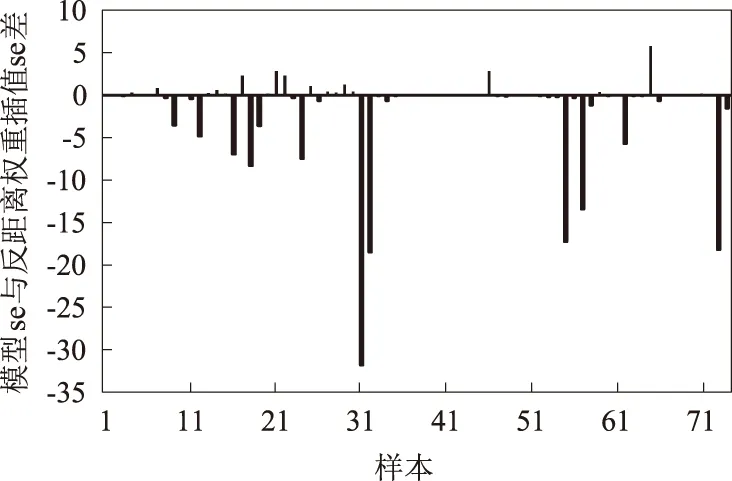
图2 模型估算值误差与反距离权重插值误差差值结果

通过分析该部分时次实测降水数据(表2)可知，当邻近站之间降水量差异较大时，神经网络模型的估算结果更优，即对局地性较强的分散降水有更好的估算能力。反距离权重插值法估算值总介于邻近站降水量最大值和最小值之间，插值结果相对稳定，其对空间分布均匀的降水有较好的估算能力；当降水局地性较强时，其估算效果较差。

表2 模型估算值、反距离权重插值估算值与实测降水量比较

2.3 模型在降水质控中的应用

对降水数据进行质控时，利用神经网络模型对待检站降水量作出估算。当估算值与实测值之间的偏差在预定范围之内时，则判断实测值正确，反之则认为实测值异常，并进行进一步检验。例如，2019年7月14日03时区域站宁河镇站1 h降水量为1.5 mm，利用神经网络模型对该站1 h降水量进行估算，估算值为19.1 mm，与原始值差异较大。对比其10个邻近区域站，除距其较远的张子铺站1 h降水量为3.9 mm外，其余各站降水量均在10 mm以上，其中大于庄站1 h降水量达到32.5 mm，宁河镇站1 h降水量明显偏低。通过对比图3(a)(b)可以看出，神经网络模型估算值更为合理。同一时次，汉沽街站实测降水量为0.1 mm，模型估算降水量35.6 mm，实测值与估算值存在较大差异。该站10个邻近站降水量如图3(c)(d)所示，离其最近(1.7 km)的汉沽国家站1 h降水量达到42.2 mm，汉沽街站实测0.1 mm降水量明显不合理。在降水质控中，除1 h降水量外，还可对3 h、6 h降水量进行模拟，并与其实测值对比，从而发现异常的降水数据。相较于人工分析，该方法具有更高的效率，并且在数据存在异常的情况下能够提供更接近真值的估算值。

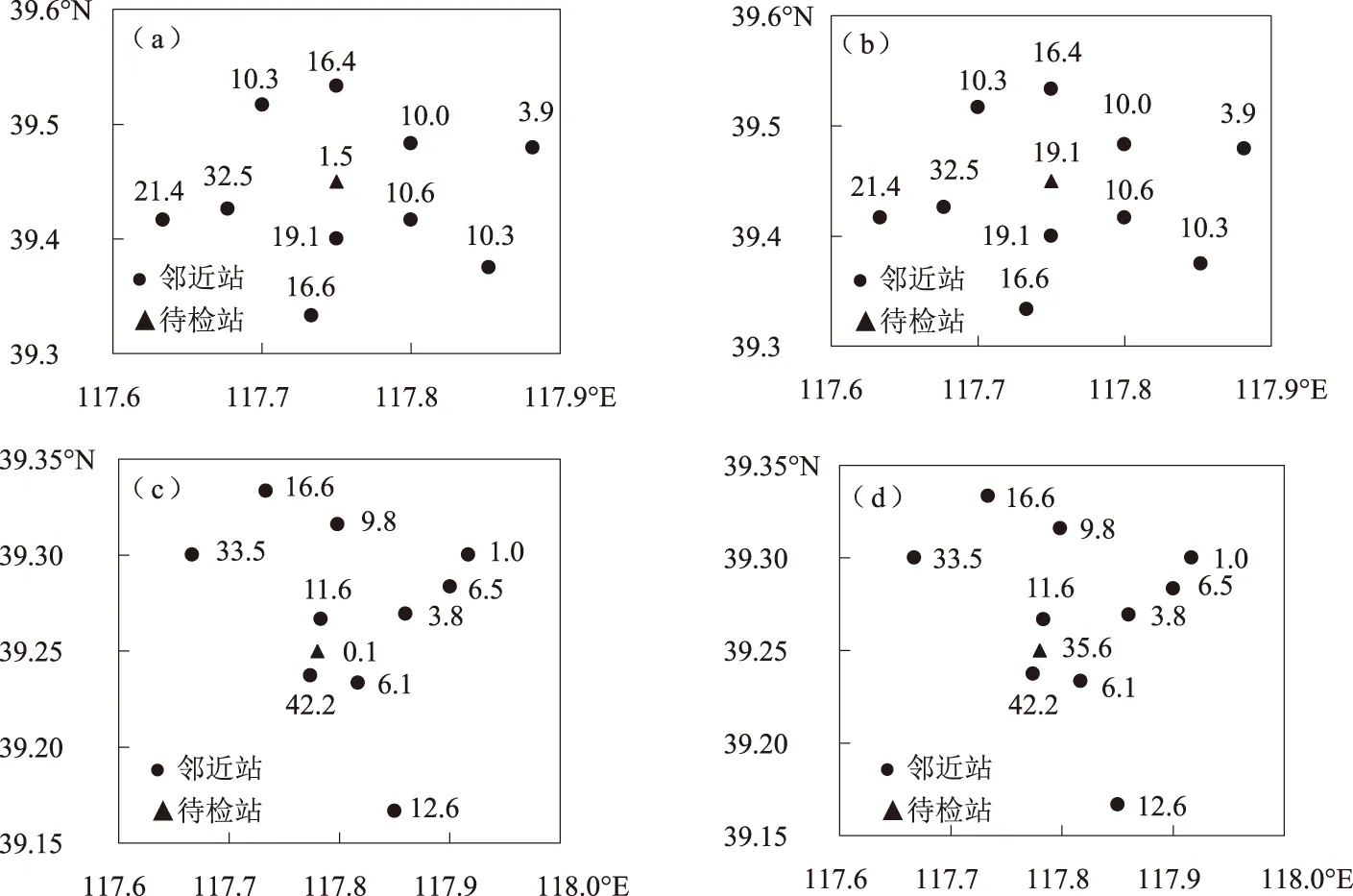
图3 宁河镇站(a)和汉沽街站(c)实测与模型估算(b、d)降水量对比单位：mm

3 结 语

基于人工神经网络算法构建了降水估算模型，比较分析了模型估算降水和反距离权重差值估算降水量的效果，并介绍了模型在降水量质量控制中的实际应用，结论如下：

(1)在实际使用过程中，应根据精度需求和运算能力设置合适的隐含层节点数。使用预训练权值作为模型初始权值可以极大提高模型的收敛速度。增大训练次数虽然可以使训练样本的均方误差不断减小，但是可能导致模型处于过拟合状态，使模型在训练样本中有较好的拟合效果，但对未知样本的预测表现一般，泛化能力较差。因此，在模型训练过程中应使用测试样本对模型进行交叉验证，防止模型过度拟合。

(2)本文质控方法结合了神经网络在数据抽象能力及空间一致检查在降水量质量控制中的优势，与利用反距离权重插值法得到的各站小时降水量插值数据相比，神经网络模型的模拟结果整体上更优。神经网络模型对局地性较强的分散降水有更强的估算能力，反距离权重插值法对均匀降水的估算效果更加稳定。因此，在实际应用中可以结合两种方法，充分发挥各自特点，使估算值更加合理准确。

(3)通过比较站点实测降水量与模型估算结果，可以及时发现异常降水数据，提升质量控制工作的效果和效率，提高自动气象站维修保障的针对性。