多因素影响下步进接触电压场路耦合模型及分析

罗玉珠，马御堂，黄继盛，周立军，石定中

（1.云南电网有限责任公司临沧供电局，云南 临沧 677000；2.云南电网有限责任公司电力科学研究院，云南 昆明 650000；3.西南交通大学，四川 成都 610000）

0 前言

配电网故障多为单相接地故障[1-2]。例如，10 kV 配电网线路发生绝缘子闪络时，故障电流通过钢筋混凝土棒流入大地[3]。这可能产生阶跃电压和接触电压，导致触电事故，严重威胁人身安全[4-5]。文献[6-7]对地电阻和地电位分布进行了数值计算，地下电场的有限元分析方法已被多次采用[8]。文献[9]研究了栅极尺寸、棒数和棒长对接触电压、跨步电压和接地电阻的影响。然而，人体在地面行走时，脚与土壤的接触面会有不同的接触面积、接触深度和接触材料。同时，考虑到电阻率的影响，触电的风险也会有所不同。然而，对于这些复杂的案例，目前还没有有效的分析方法。

因此，为了计算和分析钢筋混凝土棒周围的跨步电压和接触电压，有必要建立配电网断开时跨步电压和接触电压多影响因素的研究模型。同时，建立故障电流、阶跃电压和接触电压的协同分析模型，体现地上和地下的统一。

1 电场与电路的耦合分析

1.1 频域分析

由于配电网系统大多采用中性点不接地系统，因此，本文根据实际运行线路参数，建立了单相断路故障模型Π 类型简化等效电路模型。模型如图1所示。

在图1中，UA、UB、UC代表10 kV 交流电压源，Ra0、Rb0、Rc0代表线路阻抗，La0、Lb0、Lc0代表线路电感，C代表输电线路接地电容，Ra1、Rb1、La、Lb分别代表负荷等效电阻和等效电抗。假设故障点距离供电侧5 km。模型参数取值如下：

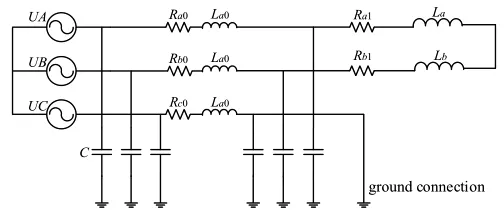
图1 配电网单相接地故障模型

Ra0=Rb0=4.74 Ω；Rc0=3.555 Ω；

La0=Lb0=153.9 mH；Lc0=115.425 H；

Ra1=Rb1=129.05 Ω；La=Lb=1.0274 H；C=0.9 μF。

故障电流Iearth由节点电压方程得到：

根据IEEE Std 80–2000，IEEE 交流变电站接地安全指南，人体电阻为1000 Ω，因此，在随后的计算分析中，人体阻力取1000 Ω 数值。假设流经人体的电流是Ib。

1.2 有限元分析

当电流流过土壤时，空间中的电流分布随时间而变化。整个土壤区域的电场和磁场不再均匀，反映了土壤的时变特性。因此，位移电流的影响在分析中不可忽略。而低频故障电流对土壤中感应电流的影响可以忽略不计。根据麦克斯韦方程(1) 和相应的材料本构方程(2)，接地装置和土壤区域的分散过程可描述如下：

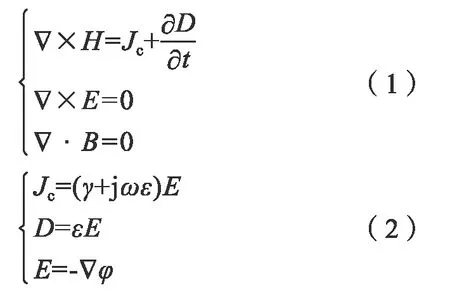
式中，H为磁场强度；Jc为全电流密度；γ代表土壤电导率；ε是介电常数；D代表电位移矢量；φ表示电位标量；E是电场强度；ω表示当前频率。

通过改变方程(1)两侧的散度，可以得到下列拉普拉斯势方程：

利用泛函定理和格林定理，方程(3)可转化为：

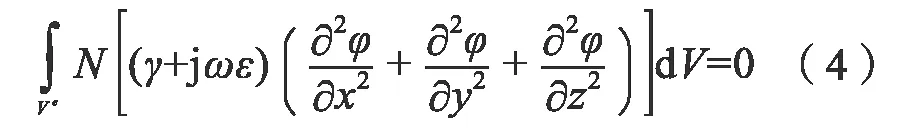
其中：N是伽辽金基函数。

通过对土壤区域四面体单元的离散处理，根据伽辽金有限元法，进一步得到任意单元中的势：

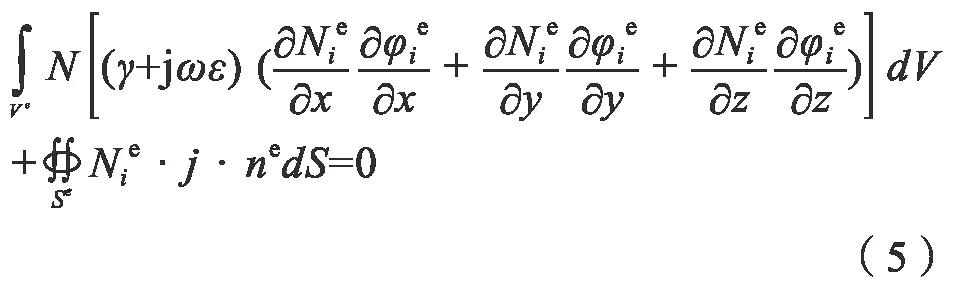
式中：Ve为元素e 的四面体，Se为元素e的外表面，J为全电流密度：

对于没有注入点的单元，方程（7）是常数，相应的单元电势满足方程（8）：

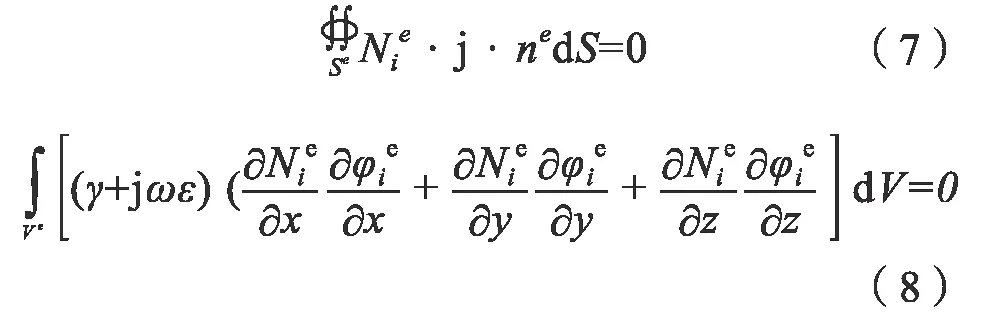
对于有注入点的装置，有两种情况，对于单相开断电流注入点：

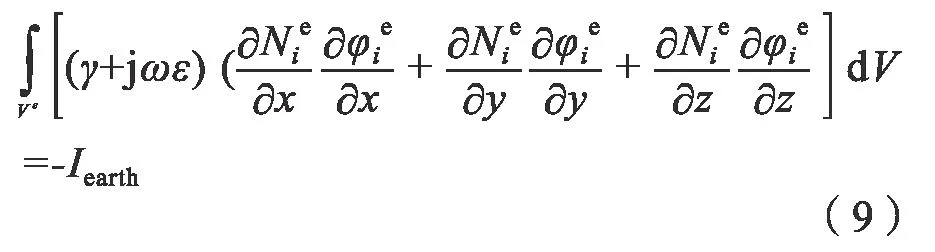
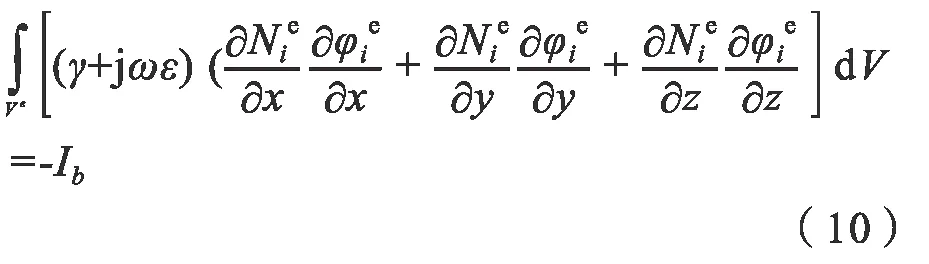
人体与地面的两个接触点：

结合方程式(8)～(10)，并施加第一类边界条件：

式中，K是有限元计算中的整体系数刚度矩阵；g是注入电流矢量。

2 模型构造

根据10 kV 配电网简化电路等效模型和人体典型等效电路，利用COMSOL 软件中AC/DC 电路模块中的电源、电容、电阻、电感等参数完成等效电路的构建。根据节点电位法连接所有电路元件，并设置所有元件的参数。

由于10 kV 配电网的输电线路大多仍处于田间和农田中，大量的钢筋混凝土杆塔仍在使用，因此本文基于钢筋混凝土杆塔进行建模。

钢筋混凝土钢筋的整体形状是一个空心圆桌。上墙半径0.14 m，外墙半径0.19 m，下墙半径0.3 m，外墙半径0.35 m。将8 根钢筋等间距嵌入混凝土钢筋中。钢筋埋于地下，地上10 m，地下2 m。

根据文献[10]，人的脚在分析中通常相当于导电金属圆盘，将金属圆盘的半径设定为0.08 m。因此，在COMSOL 中，采用两个半径为0.08 m 的金属圆盘作为人体等效电路与地下电场之间的耦合介质。

在电流流入地面60 m 处，电位降到零。在COMSOL 中，采用半球作为土壤模型进行模拟。半球半径60 m，土壤电阻率ρ=300 Ω·m。

3 模拟分析

根据IEEE 标准[10]，阶跃电压是指一个人在不接触任何接地物体的情况下，用脚桥接1 m距离时所经历的表面电位差。接触电压是指人的手同时与接地结构接触时，人的站立点的地电位升高（GPR）和表面电位之间的电位差。

计算步进电压时，距钢筋混凝土钢筋的两脚距离分别为0.3 m 和1.3 m。在计算接触电压时，假设人脚并排站立，距离钢筋1 m，钢筋混凝土钢筋上的接触位置距离地面2 m。图2和图3分别显示了计算阶跃电压和接触电压时的地电位分布。

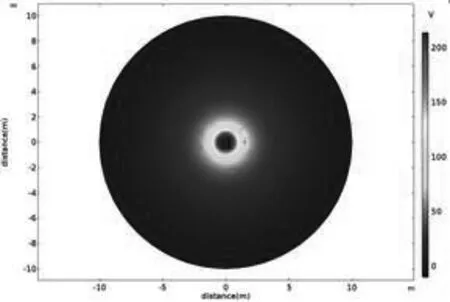
图2 阶跃电压计算下的地电位分布

图3 接触电压计算下的地电位分布

3.1 接触面积的影响

因为人的脚在不同的年龄有不同的大小，所以等效金属圆盘的面积也不同。在不失一般性的前提下，本文在传统的等效半径0.08 m 的基础上，进一步计算了等效半径分别为0.04 m、0.06 m、0.1 m 和0.12 m。

图4可见，随着人体与地面接触面积的增大，阶跃电压几乎呈线性上升趋势。相比之下，如图5所示，虽然接触电压随着接触面积的增加而增加，但趋势明显减慢。

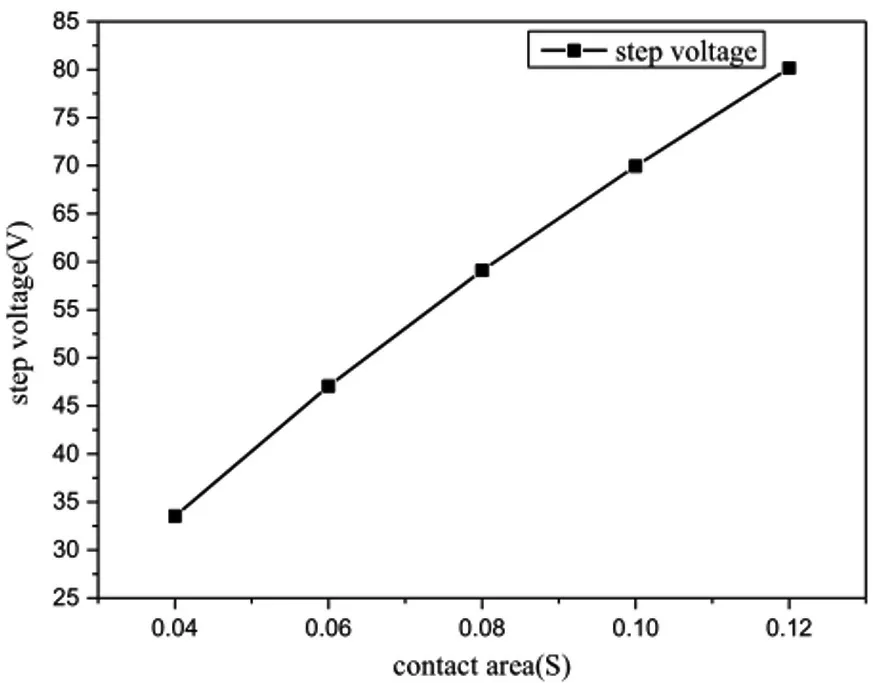
图4 接触面积对阶跃电压的影响

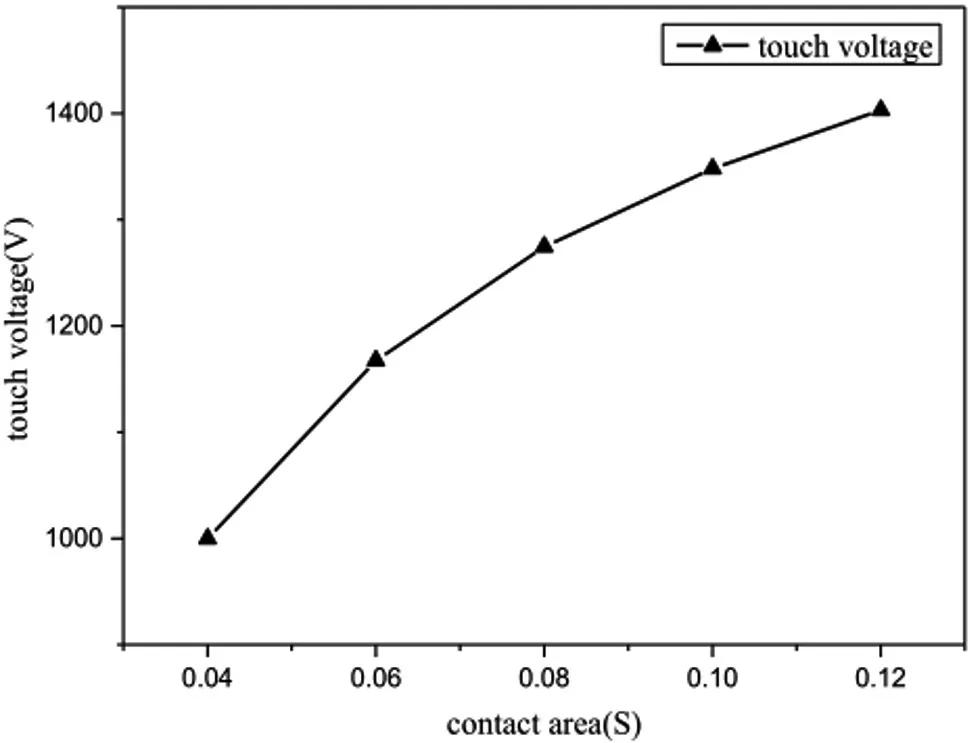
图5 接触面积对接触电压的影响

随着圆盘面积的增大，最明显的变化是圆盘外缘更靠近钢筋混凝土。换句话说，电压测试点更靠近故障电流流入的位置。考虑到电流在地面扩散时表面电位迅速降低，阶跃电压必然增大。测量接触电压时，故障电流同时流经钢筋混凝土棒和人体。随着距离越来越近，流经人体的电流会增加，接触电压也会增加。

3.2 人足埋深的影响

图6和图7是在0.08 m 半径不变的情况下，改变金属盘埋深时的阶跃电压和接触电压的计算结果。

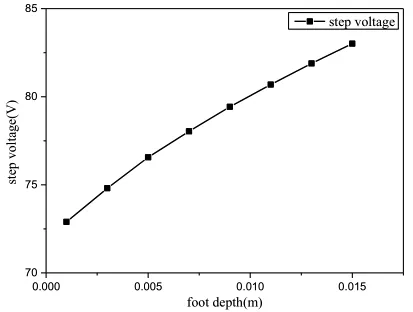
图6 脚深对阶跃电压的影响

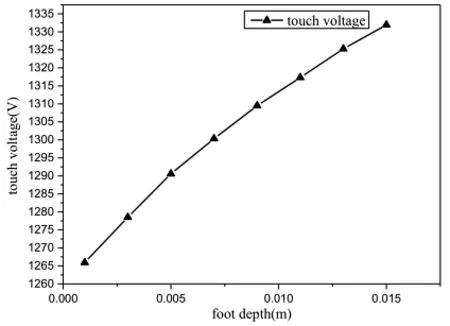
图7 脚深对接触电压的影响

根据镜像法，从点电源在周围土壤中任意一点产生的电势的计算公式来看，脚埋得越深，脚离点电源越近，离点电源的镜像点越远。因此，脚部的电压升高，步进电压也升高。计算公式如下：

式中，r为点到电源的距离；r′为点到电源镜像点的距离。

在计算接触电压时，故障电流同时通过钢筋混凝土杆和人体向土壤中传播。当人足埋深时，人足与周围土壤接触较多，断层电流更容易分散。因此，通过身体的电流增加，接触电压也增加。

不同体重的人对地面施加不同的压力。随着体重增加，身体深入地面，脚上的电压必然会增加。特别是在潮湿的土壤中，重量变化引起的电压变化更大。

3.3 电阻率的影响

绝缘子闪络常伴有雷暴，雷暴通常是由雷击绝缘子引起的。雷暴意味着钢筋混凝土钢筋潮湿，电阻率较低。同时，土壤电阻率也发生变化。电阻率的变化对阶跃电压和接触电压的计算有很大的影响。钢筋混凝土钢筋电阻率对阶跃电压和接触电压分别如图8、图9所示，土壤电阻率对阶跃电压和接触电压分别如图10、图11所示。

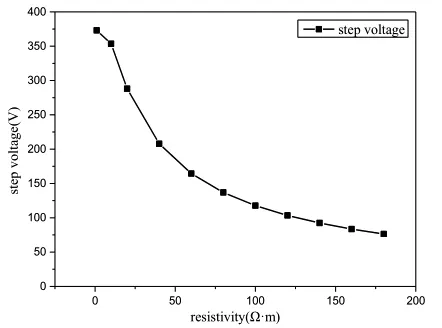
图8 钢筋混凝土钢筋电阻率对阶跃电压的影响

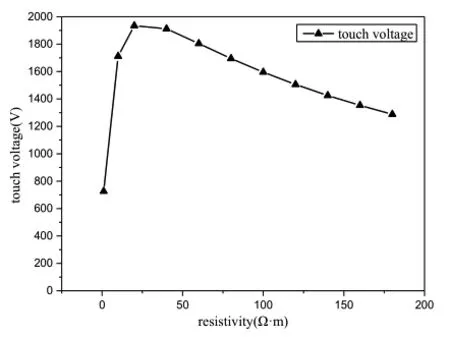
图9 钢筋混凝土钢筋电阻率对接触电压的影响

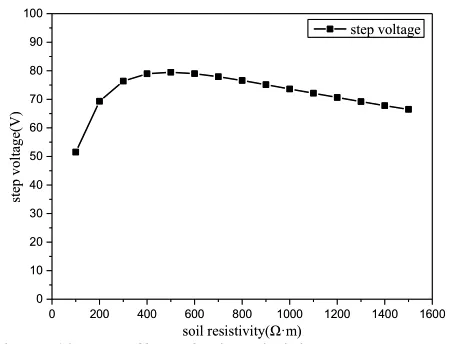
图10 土壤电阻率对阶跃电压的影响

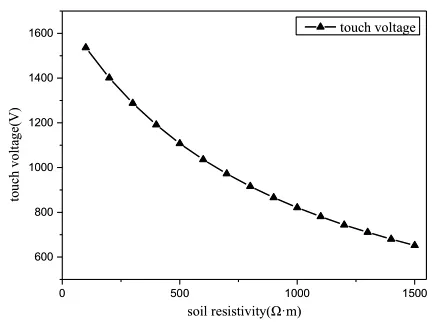
图11 土壤电阻率对接触电压的影响

随着钢筋电阻率的增大，阶跃电压减小，接触电压先增大后减小。而随着土壤电阻率的增大，阶跃电压先增大后减小，接触电压逐渐减小。

为了便于分析，将具有相同趋势的曲线放在一起。当钢筋混凝土的电阻率从1 Ω·m～180 Ω·m、阶跃电压下降79.53%；当土壤电阻率从100 Ω·m ～1500 Ω·m、接触电压下降57.57%。由图9和图10可知，曲线上升率和下降率分别为166.31%、48.20% 和32.65%、16.35%。

3.4 接触面材料的影响

上述计算考虑了极端电击，即不考虑鞋对电压的影响。考虑鞋的影响，计算条件为：接触面半径0.08 m，人脚埋深0 m，钢筋混凝土电阻率180 Ω·m、土壤电阻率300 Ω·m。不同材料对阶跃电压和接触电压的影响如表1所示：

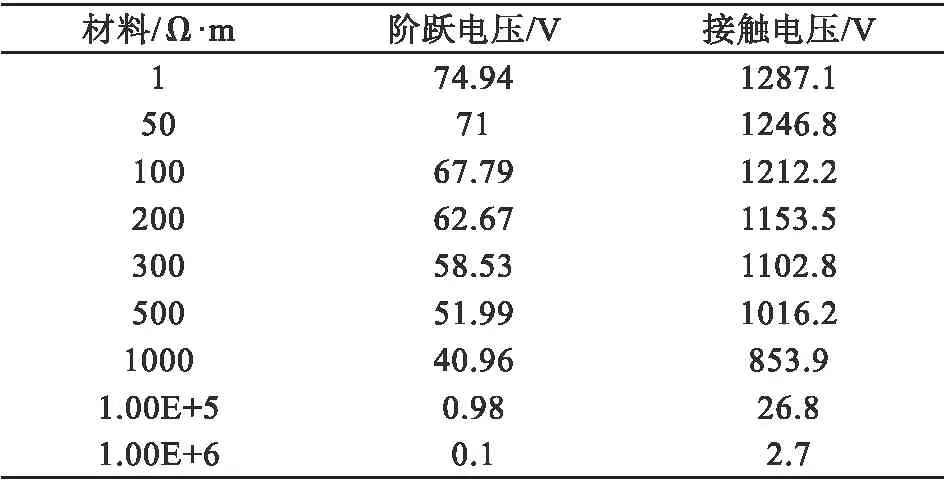
表1 材料对阶跃电压和接触电压的影响

随着材料电阻率的增加，阶跃电压和接触电压急剧下降。当体积电阻率远小于普通鞋底时（橡胶，1013Ω·m），步进电压为0.1 V，接触电压为2.7 V，不会引起触电。

4 结束语

1）人体足部接触面积和深度与阶跃电压和接触电压呈正相关。

2）当考虑接触面材料时，阶跃电压和接触电压急剧下降。当绝缘性能达到106Ω·m、人们几乎不会触电。

3）在人体电路的影响下，阶跃电压随钢筋电阻率的增大而减小，接触电压先增大后减小；随着土壤电阻率的增大，阶跃先增大后减小，接触电压逐渐减小。