基于改进后灰狼群体智能算法的校园节能系统方案设计

夏青楠 于蒙 韩瑜进 郝嘉明

引言

校园能源浪费问题一直是社会的热点话题之一，校园内的用电设施种类多，人员密度大，人员流动性强等因素都使校园的能源使用难以进行管控。如今国内外对此类问题的研究主要分为以下三个方面，一是对单一用电设备进行智能化改造，如声光控节能灯具；二是在管理层面更好地安排校内人员使用用电设备；三是设计整套的节能系统来调控校园能源的使用。

而现阶段的校园节能系统普遍存在系统响应时间长、控制设备种类单一等问题，使电能调配无法根据温度、时间、人员的流动等因素进行实时响应。而节能系统的响应时间主要由算法决定，在解决此类资源分配问题的过程中，蔡柳萍提出了一种基于改进遗传算法的云计算数据中心资源分配算法[1]，李炳坤将针对不可分物品的局部无嫉妒资源分配问题，转变为可满足性模块理论问题进而进行求解[2]。国外学者也同样提出了多维资源分配问题的M-best算法和LP based算法[3-4]，并研究了遗传算法在组织系统中的资源分配问题的应用[5]。但以上算法的求解精密度偏低，且算法较为冗杂。[6]

本文从电源调配模型入手，提出了一种启发式离散灰狼优化算法求解校园电能资源分配问题并应用于实际验证算法的可行性。

一、电能调配优化模型——多变量多约束非线性优化节能方法模型

校园节能系统模型即每个房间在不同时间段内对其电能分配量进行整体协同控制，在楼栋供电电源的总可调功率范围内，保证每个用电器的合理负载，保证整个楼宇内的用电器能够连续高效运行；同时尽量减少电能调节频率，增加楼栋中电能设备的机械使用寿命。依据教室中常用电器的工作时间长度和每周不同时间段内教学楼中正在工作的用电器数量为算法的优化对象，设计出了一个非线性的多目标电能调配函数。[7]其具体表征如下所示：

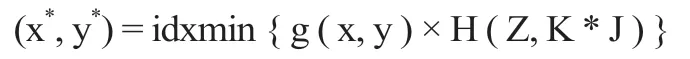
其中 x=[x1,x2,...,xn]T，x 代表工作时长，x∈R+；y=[y1,y2,...,yn]，y 处于工作状态的用电器的具体数量，y∈N+；n 表示用电设备的序列编号，n∈N ；g(x,y) 是同耗能率有关非线性函数；K=[K1,K2,...,Kn]，K 为模型中的相关系数，K∈R+；J 为用电设备每小时的耗电量，J=[J1,J2,...,Jn]，J∈R+；参数 Z 是判断工作日的参数表征量，其取值情况如下：

作为校园节能系统实现的核心，模型的算法设计是提高整个校园用能系统最终用能效率的动力源。算法的核心涵义在于挖掘事件的内核驱动规律并对其进行模拟，根据模拟成果对事件进行预测，用最小的工作量换取最大的成果。[8]

二、校园用能调配算法设计

本文采用改进后的灰狼算法，采用非支配排序遗传算法求解多目标优化模型，并通过模糊隶属度法对生成的解集进行滤波选出最优。[9]以实数编码的加速灰狼优化算法为基础对能源网进行经济调度优化，来达成对电能利用的最优调度，远程控制终端设备，以达到节能的目的。

（一）基本原理

灰狼算法效仿原始动物群体的等第规章与捕猎行为。所有的数据群被分为α、β、δ、ω四组。α、β、δ这三组根据次序是对模型响应程度最好的三个数据群，而后这三个数据群引导其他的数据群向着最优目标敛迫。在这整个敛迫过程中，不断更新α、β、δ、ω数据群的位置，直到能够找到最优解。式（1）表征各个群体之间的距离，式（2）表征数据个体的更新方式。

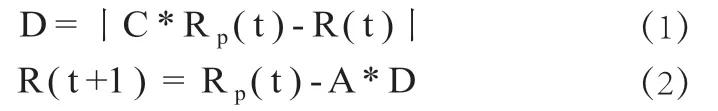
其中：D表征数据群与最优解的距离大小；t 表征算法当前的迭代次数；A 表示算法中的随机向量，C 表示算法中的自适应向量，其中 A=2a * r2- a ；C=2r1；Rp是表征当前最优解的位置远近，R 是表征当前数据集与最优解的位置向量。

（二）引入基于非线性收敛因子策略

灰狼优化算法自问世以来就凭借其优异的求解能力受到了极大的重视，但这种优异求解能力也为其带来了很多缺陷，敛迫速度不理想、整体搜寻能力较弱，在敛迫过程中，灰狼优化算法尤其易表征出局部最优，而不是总体最优。普通灰狼算法的收敛因子 a 随着迭代次数由2线性减少到0。[10]这种线性的敛迫递减优化不能映射出算法的优化敛迫思想，还会导致敛迫速度减缓，为增加其收敛速度，引入一种非线性反余弦收敛因子，增加其收敛速度，更快地划定各个用电器的最优电能调配范围。

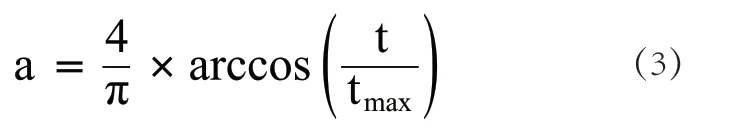
上式中：t 代表当前算法迭代寻优的次数；而则代表着进行当前步骤时的最大迭代次数。

（三）引入动态权重策略

当算法判断出各个用电器的最优电能调配范围时，伴随α、β、δ这三个数据集不断地向最优调配结果接近，但是灰狼算法的总体搜寻能力较弱，其α数据集不一定是全局解算最优位置，这就会导致在进一步的敛迫过程中，容易得出局部的最优解，在此引入一种基于引导点和向量模长的比例权重方案，平衡电能调配的总体水平，实现智能教学楼的电能调配总体最优。

在改进后灰狼算法中，ω狼集合了三头指导狼的导引，向最优点敛迫。

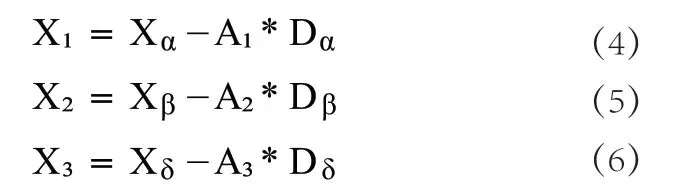
表1 权重比例计算公式

最终迭代方式：

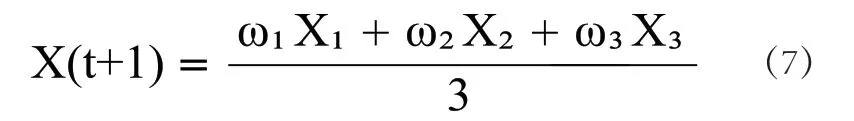
三、试算验证

群体智能算法的性能优劣体现在两方面，其中一个是全局搜索能力，即从整体挖掘最优点的能力，而另一个则是局部搜索能力，即针对够局部算法进行开发的能力，以提高算法的精度。[11]怎么样在这两方面之中找到一个均衡点是算法获得较高敛算性的核心问题。

为了进一步验证算法敛迫能力，本文通过选择 g1，g2，g3这三个常见的测试函数对改进后的函数计算性能进行验证。其中包括复杂单峰测试函数 g1和复杂多峰测试函数 g2，g3测试函数信息如下表所示：

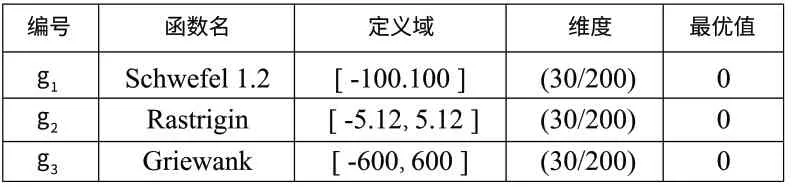
表2 测试函数信息

计算机仿真时所采用的基本配置是Microsoft Window 64位操作系统，计算环境为Matlab2016。

（一）非线性收敛因子仿真分析

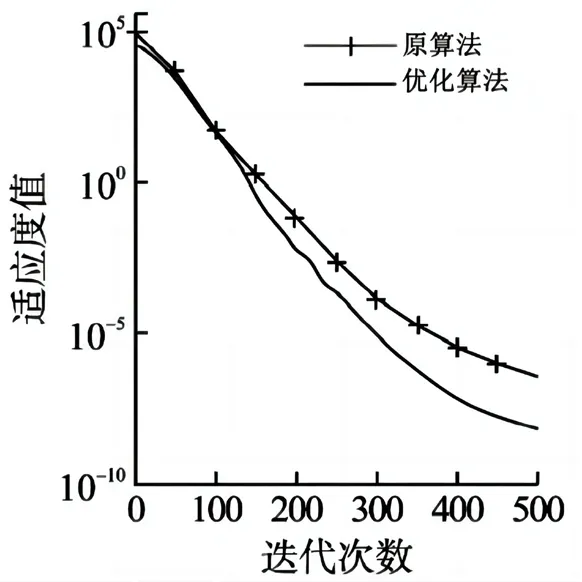
图1 g1寻优结果

图2 g2寻优结果

由图中可以看出，单独引入新提出的非线性收敛因子在算法性能上有提升，但是仍有很大的提升空间，在单峰值实验函数 g1和多峰值实验函数 g2的寻优过程中，算法没有找到理论上的最优解答。这是因为初始化时，电能的分布较为分散，随机性较强，尽管单独引入新的敛算因子提升效果并不是很好，但是进行其他持续的算法改进后，对于算法的求解能力会有一定优化。

（二）引入动态权重策略仿真分析

通过前面的仿真测试，采用非线性收敛因子的算法在一定程度上提高了算法的收敛速率，但是其寻优结果并不优越，对于算法在寻找最优调配点的过程中易陷入局部最优的问题，本文通过引入动态权重策略来进行仿真，避免这种问题的发生。测试前提设定，测试函数的维度为dim=30，测试中的最大迭代次数为，对单峰值实验函数 g1和多峰值实验函数 g3进行模拟，测试结果如下图所示。

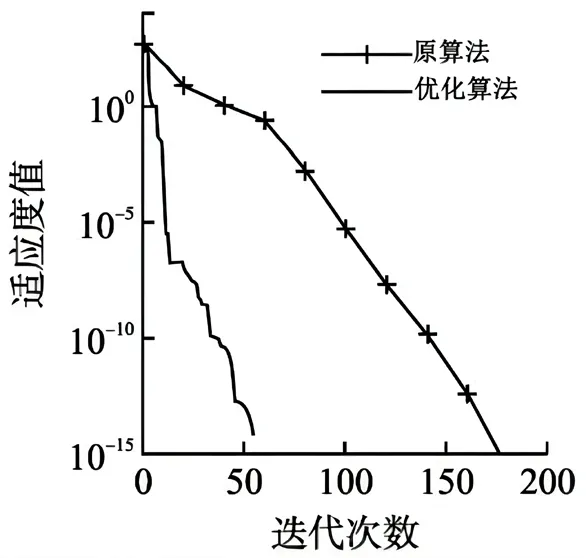
图3 g1寻优结果

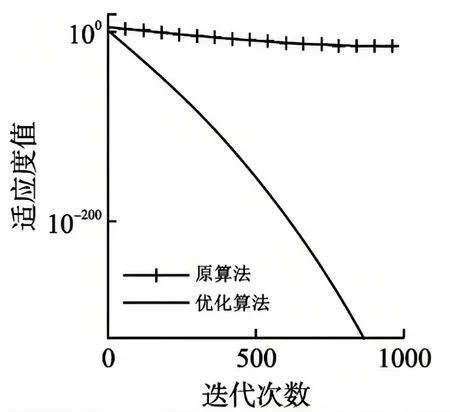
图4 g3寻优结果

由图中数据可以得到，在引入动态权重策略后，优化后的灰狼算法在单峰函数 g1和多峰函数 g3上能找到最优值0，引入改进动态权重策略的算法能够找到整体最优，大幅度提高了收敛效率。仿真测试证明，引入动态权重策略的灰狼算法在收敛精度和寻找整体最优的效能上有很大提高。

总结

以降低校园整体能耗为出发点，建立多变量多约束非线性优化节能方法模型，设计了采用灰狼群体智能算法的校园节能系统。经试算验证，可得出以下结论：（1）灰狼群体智能算法的非线性算法相较于线性算法具有前期求解范围大，后期求解效率高的特点。（2）设计出的基于改进后灰狼群体智能算法的校园节能系统节能效果明显，节能率预计可达10%-25%。