基于蚁狮优化算法的主动配电网优化调度

赵玉芝

（广州致新电力科技有限公司，广东 广州 510000）

0 引言

随着能源危机的到来和人们环保意识的提高，大力开发和使用可再生能源成为解决能源和环保问题的重要举措[1]。但是风能、太阳能等可再生能源具有较大的随机波动性，大量接入配电网会破坏系统稳定性[2]。为了解决这一问题，高效、灵活的主动配电网（Active Distribution Network，ADN）正在逐步取代传统配电网[3]。但目前ADN 运行成本相对较高，如何对其进行经济、合理的调度是目前亟待解决的问题。目前，人们提出了一些降低ADN 运行成本的优化调度方法。文献[4]为了提高ADN 运行的经济性，以配电网总运行成本最小为目标函数，建立了ADN 分层经济优化调度模型，采用交替方向乘子法对模型进行了求解，获得了最优解。文献[5]综合考虑了ADN 在运行过程中产生的各项成本及约束条件，并采用分时电价计算与大电网的功率交互成本，建立了基于狼群算法的ADN 经济优化调度模型，并通过实际算例验证了模型的实用性。文献[6]对遗传算法的交叉概率和突变概率进行了改进，提出了一种改进遗传算法，采用改进遗传算法进行AND 经济优化调度，取得了良好的效果。上述ADN 优化调度模型只考虑了运行成本，而忽略了燃气轮机的使用带来的环境成本，因此ADN 优化调度模型有待进一步研究。该文以主动配电网经济成本和环境成本组成的综合成本最小为优化目标，综合考虑各类约束条件，建立基于蚁狮优化算法的主动配电网经济优化调度模型，并通过实际算例进行仿真分析，对模型的正确性和实用性进行验证。

1 ADN 优化调度模型

1.1 目标函数

建立ADN 优化调度模型时，除了要考虑主动配电网运行过程中的经济成本外，还应当考虑微型燃气轮机使用过程中产生的污染物带来的环境成本[7]。

1.1.1 经济成本

AND 经济成本主要包括输电网成本、备用容量成本、分布式电源的维护成本和储能设备的维护成本。AND经济成本的数学表达式如公式（1）所示。

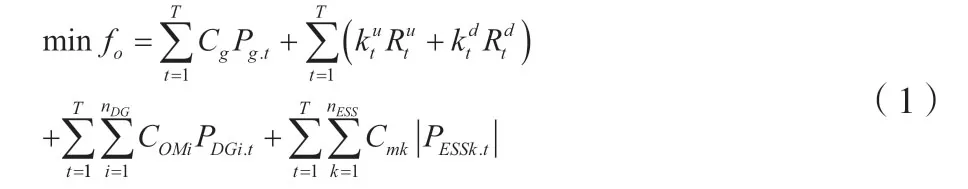
式中：T为调度周期；i为分布式电源的数量；k为储能设备的数量；Pg.t为t时刻输电网功率；PDGi.t为t时刻分布式电源的输出功率；PESSk.t为t时刻储能设备的输出功率；Rtu为备用容量的有功功率；Rtd为备用容量的无功功率；Cg.t、ktu、ktd、GOMi和Cmk均为成本系数；PESSk，t为t时刻第i个储能设备的充放电功率。

1.1.2 环境成本

环境成本主要包括资源消耗成本和污染物排放成本。ADN 环境成本minfe如公式（2）所示。

式中：s为产生污染气体的发电单元个数；j为污染气体种类；Q为污染气体的排放量；Cen为能源消耗系数；Cf为惩罚系数；N为发电单元总数；n为污染气体类型总数。

1.1.3 综合成本

综合成本由经济成本和环境成本共同组成，其表达式如公式（3）所示。

1.2 约束条件

1.2.1 支路潮流约束

配电网在运行过程中应保持有功功率和无功功率的平衡，其表达式如公式（4）所示。

式中：nl为系统节点总数；nL为系统支路总数；PDl.t为节点有功功率；QDl.t为节点无功功率；PlossL.t为支路损失的有功功率；QlossL.t为支路损失的有功功率。

1.2.2 节点电压约束

系统内各节点电压应在一定范围内波动，不能超过额定值，其约束如公式（5）所示。

式中：Ul，t为节点电压幅值；分别为节点电压幅值的最大值和最小值。

1.2.3 馈线容量约束

馈线容量约束如公式（6）所示。

式中：SL，t为馈线容量；分别为馈线容量的最大值和最小值、下限。

1.2.4 系统备用容量约束

系统备用容量约束如公式（7）所示。

1.2.5 分布式电源出力约束

各类分布式电源出力均受到额定功率的限制，其约束如公式（8）所示。

1.2.6 储能设备约束

储能设备约束分为容量约束和输出功率约束，具体如公式（9）所示。

式中：SOC.t为储能设备的容量；SOCmin、SOCmax分别为储能设备容量的下限和上限；PESSc、PESSd分别为储能设备的最大放电功率和最大充电功率。

2 蚁狮优化算法

2015 年，Mirjalili 等人根据自然界中蚁狮猎捕蚂蚁的行为提出了ALO 算法[8]，其中心思想是通过蚁狮狩猎机制实现全局寻优，基于蚂蚁的随机游走提高搜索能力，采用轮盘赌法保证种群的多样性，并用精英策略确保算法的优化性能。ALO 算法的原理如下。

自然界中蚂蚁随机游走的数学表达式如公式（10）和公式（11）所示。

式中：K（t）为蚂蚁游走步数的集合；cumsum为计算累加和；t为迭代次数；Tmax为算法的最大迭代次数；r（t）为随机数；rand为随机函数，取值为[0，1]。

蚂蚁在游走时受到边界的限制，需要进行归一化处理，如公式（12）所示。

式中：ai、bi分别为变量i游走边界的最小值和最大值；、分别为第t次迭代时变量i的最小值和最大值。

蚂蚁在边界游走时会碰到蚁狮制造的陷阱，其表达式如公式（13）所示。

式中：ct、dt分别为第t次迭代时所有变量中的最小值和最大值；为第t次迭代时蚁狮j所在的位置。

在狩猎过程中，一只蚁狮只能捕获一只蚂蚁，蚁狮适应度值越大，捕获蚂蚁的可能性越大，轮盘赌法决定了某只蚁狮具体捕获哪只蚂蚁。为了防止蚂蚁逃走，蚁狮采用抛沙的方法迫使蚂蚁游走范围快速收缩，该过程的数学表达式如公式（14）和公式（15）所示。

式中：I为比例系数；v为随迭代次数不断增大的变量。

根据精英策略，每次迭代完成后找出蚁狮中适应度值最好的个体，在轮盘赌法和精英策略的共同作用下，蚂蚁位置的表达式如公式（16）所示。

最终，当蚁狮适应度值超过蚂蚁适应度值时，蚁狮将蚂蚁捕获，如公式（17）所示。

式中：为第t次迭代时蚂蚁q的位置。

3 ALO 算法求解ADN 优化调度模型

该文采用蚁狮优化算法求解主动配电网优化调度模型，相关流程如图1 所示，具体步骤如下：1）输入ADN 运行参数，包括调度周期、节点阻抗、负荷及分时电价等。2）设置ALO 算法的相关参数，并初始化种群，生成蚁狮和蚂蚁种群。3）根据公式（3）计算种群初始适应度值，并选择其中的最优个体作为精英蚁狮。4）采用轮盘赌法确定蚁狮和蚂蚁的位置，并将其一一对应。5）利用公式（4）～公式（7）更新蚂蚁和蚁狮的位置，并确定精英蚁狮。6）判断ALO 算法是否达到最大迭代次数，如果是，则输出最优解，否则返回步骤4。采用ALO 算法对ELM 的权值和阈值进行优化，设置空间维数为2，蚁狮数量为70，最大迭代次数为200。

图1 ADN 优化调度模型求解流程

4 算例分析

该文采用IEEE 33节点配电系统进行主动配电网优化调度仿真分析，其网络拓扑结构如图2 所示。在图2 中，WT表示风力发电机，WT 接入节点7；MT 表示微型燃气轮机，MT 接入节点29；PV 表示光伏电源，PV 接入节点31；ESS表示储能设备，ESS1 和ESS2 分别接入节点20 和节点7。

图2 网络拓扑结构图

设置调度周期为24h，调度日当天的风电出力、光伏出力及负荷变化情况如图3 所示。

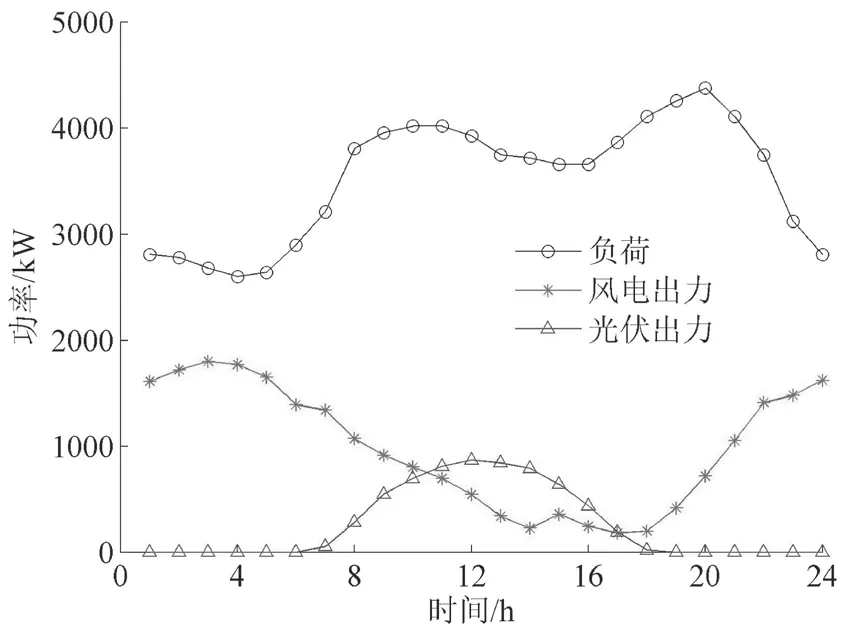
图3 系统负荷、风电光伏出力情况

在MATLAB 中进行仿真分析，蚁狮数量为70，最大迭代次数为300，采用蚁狮算法对AND 优化调度模型进行求解，ALO 算法的迭代寻优曲线如图4 所示，为了对比验证ALO算法的优越性，采用PSO 算法对该文的目标函数进行求解，PSO 算法的参数设置可参考文献[9]，图4 中同时还给出了PSO 算法的迭代曲线。根据图4 可知，ALO 算法只需要70次迭代即可找到最优解，其最优解为24192 元。而PSO 算法需要137 次迭代才能找到最优解，其最优解为24392 元。由此可见，ALO 算法的优化效果更好。

图4 ALO 算法和PSO 算法的迭代曲线对比

输电网、微型燃气轮机和储能设备的处理情况如图5～图7 所示。根据图5～图7 可知，输电网和微型燃气轮机在12h～24h 出力较大，在0h～12h 出力较小。而储能设备在用电高峰期放电，在用电低谷期充电，能够很好地起到功率调节的作用。

图5 输电网功率变化图

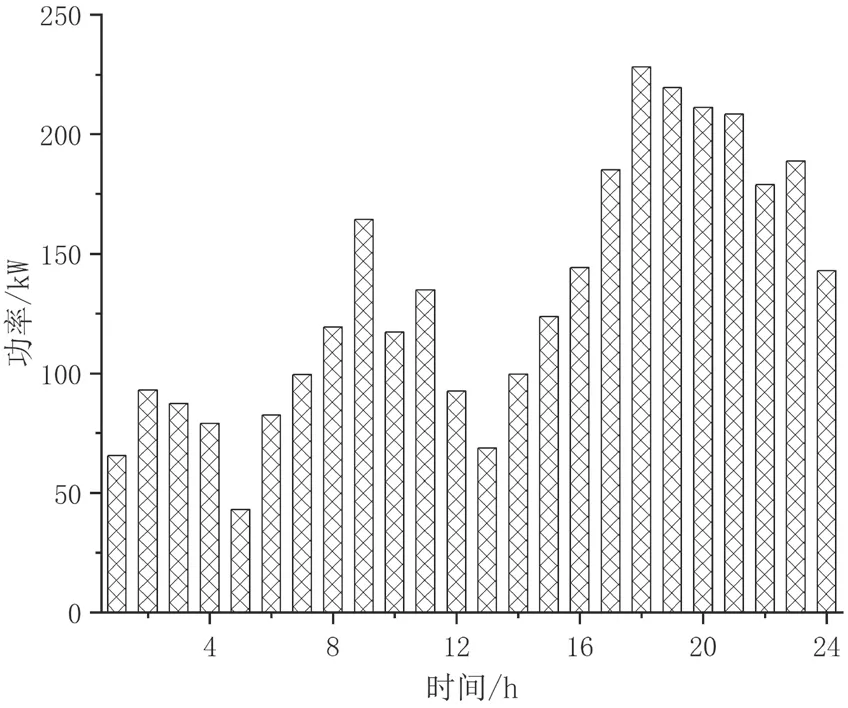
图6 微型燃气轮机输出功率变化图

图7 储能设备功率变化图

5 结论

该文以主动配电网系统综合成本最小为目标函数，综合考虑各类约束，建立了基于蚁狮算法的主动配电网优化调度模型，采用IEEE 33 节点配电系统进行算例分析。结果表明，ALO 算法只需要70 次迭代即可找到最优解24192 元，比PSO算法的优化效果更好，验证了模型的正确性和优越性。