河口回水动力的演变过程及其影响机制−以长江河口为例
2022-02-04古俊豪蔡华阳杨昊李博
古俊豪,蔡华阳*,杨昊,李博
(1.中山大学 海洋工程与技术学院 河口海岸研究所,广东 广州 510275;2.河口水利技术国家地方联合工程实验室,广东广州 510275;3.广东省海岸与岛礁工程技术研究中心,广东 广州 510275;4.南方海洋科学与工程广东省实验室(珠海),广东 珠海,519000)
1 引言
河口是陆海交汇的特殊地带,亦是径流和潮流耦合作用的重要场所。由于密度梯度、潮汐不对称、径流以及径潮相互作用的共同影响,河口的平均水位(或余水位)向陆方向逐渐升高,这种现象称之为回水效应,对应的区域为河口的回水区[1]。河口的回水区因其独特的径潮动力耦合及其非线性作用,直接影响河口的潮波传播、洪水下泄、泥沙冲淤等过程[2–5]。因此,探讨河口回水动力的演变过程及其影响机制对防洪体系的构建、河道取水工程设计、航道的整治规划等水资源的高效开发利用具有重要科学意义。
根据回水效应的动力学特点,部分学者根据沿程河段与上游河段的水面线形态差异,提出各种回水特征长度公式用于探讨回水区的动力学过程及机制[5–7]。这些公式被众多学者广泛应用于密西西比河、格兰德河等径流影响较大的河流系统,在研究回水区的河床冲淤与回水曲线的关系、回水界限上游和下游河道地形的长期演变、三角洲决口位置与回水区非均匀流侵蚀效应的联系等方面起到关键作用[5,8–10]。虽然回水动力及其在河床演变中的应用已取得丰硕研究成果,但相关回水理论在河口径潮相互作用区域的应用尚有较大局限,主要原因在于河口区域潮汐动力对回水区的动力学影响机制尚不明确,亦缺乏类似潮汐淡水区(Tidal Freshwater Zone)系统的特征分界方式(即微咸水的上游界限、双向潮流的上游界限,以及潮位波动的上游界限)[11]。因此,考虑潮汐作用及其对回水动力的影响过程及机制仍是河口动力学有待深入研究的重要科学问题。
根据回水效应的定义,河口回水区长度的变化主要受控于径潮动力的相互作用。研究表明,余水位梯度是定量分析回水区径潮动力相互作用的关键要素,根据一维圣维南方程,该要素主要与非线性摩擦项相平衡。采用切比雪夫多项式分解方法可将非线性摩擦项分解得到控制余水位梯度变化的径流因子、潮流因子和径潮相互作用因子,进而揭示河口区径潮动力驱动下余水位梯度的形成变化机制[12–15]。已有研究表明,上游下泄流量是河口区回水动力季节性演变的主控影响因子,但口门处不同分潮波亦会对余水位梯度的形成及回水曲线形态产生重要影响[2,16–17]。河口回水区不同区段余水位的主控因素(径流、潮流及径潮相互作用因子)具有空间差异性,且存在明显的洪枯季及大小潮变化[18]。因此,余水位梯度解析分解是研究河口回水动力过程及其影响机制的有效切入点。
本文在经典河流回水理论的基础上,聚焦河口潮汐引起的回水效应问题,基于径潮动力耦合条件下潮波传播的一维水动力解析模型[18],重新定义河口回水区上游界限(回水界)并提出相应的界定方法。通过给定不同径潮动力组合,并以长江河口为例,探讨河口回水动力演变过程及其影响机制,拓展经典河流动力学的回水理论,为河口区的防洪、供水、通航及水资源调配等提供科学依据。
2 研究区域与数据
长江自西向东横贯中国中部,是我国的第一大河流。大通以下的长江河口是典型的感潮河段,到天生港总长约454 km,受上游径流和外海潮流的共同控制。以天生港、徐六泾潮位站为参考,长江河口多年平均潮差分别为1.97 m、2.15 m,属于中潮型河口[19]。长江河口潮汐具有典型的不规则半日潮特征,涨潮和落潮的平均历时分别为5 h 和7.4 h[20]。根据大通水文站2003–2014 年的观测资料,长江河口流量季节性变化显著,夏季(6–8 月)最大流量为64 700 m3/s,冬季(12 月至翌年2 月)最小流量为8 380 m3/s,多年平均流量为26 500 m3/s。
为研究长江河口回水界的季节性变化特征及其影响机制,本文收集2003–2014 年大通水文站的月均流量数据,以及天生港、江阴、镇江、南京、马鞍山、芜湖6 个潮位站的月均潮位数据和月均潮波振幅数据(通过月均高、低潮位估算)。数据来源于长江水利委员会。沿程潮位站水位观测值均已统一转换至1985 国家高程基准。不同于以往对长江河口口门附近区域水动力的研究,本文主要关注天生港以上长江河口主干河道的径潮动力变化,以天生港作为研究区域的外海边界。江阴、镇江、南京、马鞍山、芜湖与天生港的距离分别为46 km、155 km、236 km、284 km、330 km(图1)。
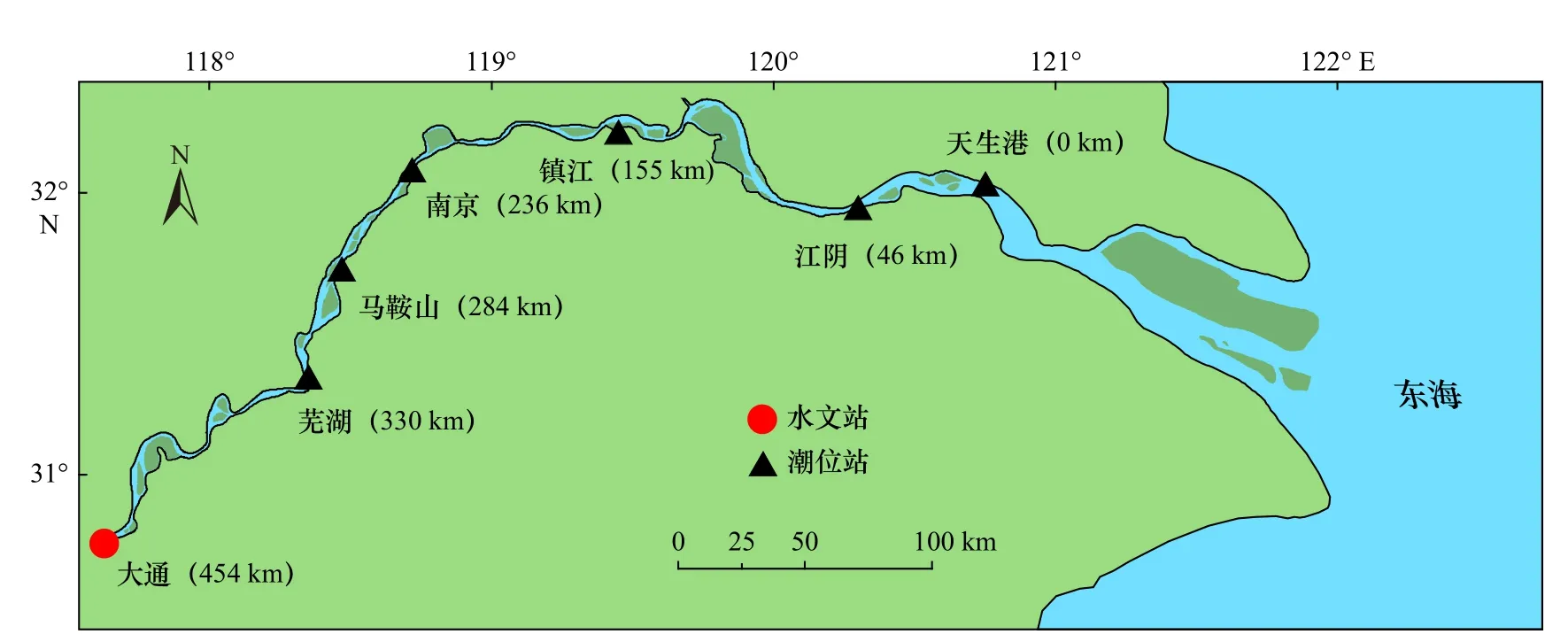
图1 长江河口位置Fig.1 Location of the Changjiang River Estuary
3 研究方法
3.1 河口地形概化
经典河流动力学中关于回水效应的机制分析和解析解均是在恒定河宽和线性底床高程条件下,结合线性化摩擦项得到的。但在河口区域,实际河宽一般由海向陆逐渐辐聚并收敛,这种河宽变化特征已被国内外学者广泛应用于河口区域的水动力模型研究[21–23]。因此,本文采用河宽B沿程呈指数形变向内陆收缩、底床高程Zb呈线性变化的概化地形:
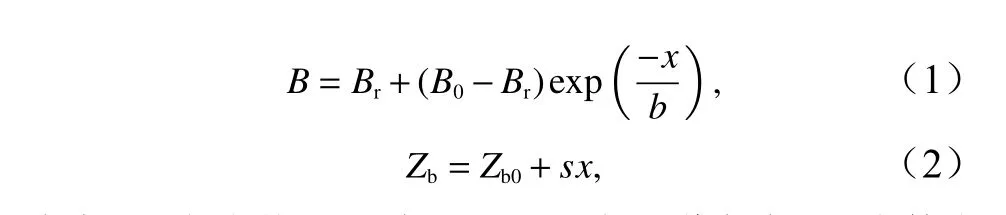
式中,Br为收敛至上游河段的最小河道宽度;B0为外海边界处河道宽度;x为外海边界向上游延伸的距离;b为河道宽度的辐聚长度;Zb0为外海边界处底床高程;s为线性底床坡度。河口沿程的潮平均水深可由下式给出:

3.2 一维水动力解析模型
河口一维动量守恒方程可表示为[24]

式中,Z为自由水面高程;t为时间;g为重力加速度;ρ为河水密度;K为Manning-Strickler 摩擦系数(即曼宁系数的倒数);h为河道水深;U为断面平均流速,由径流流速Ur和潮波流速Ut两部分组成,即

式中,υ为潮波流速的振幅;ω为潮波频率;Q为流量。
潮平均条件下,斜压梯度项(即密度梯度项)和惯性加速度项对余水位的影响均为小量[12],因此对式(4)进行潮周期平均,可得余水位梯度的简化表达式为
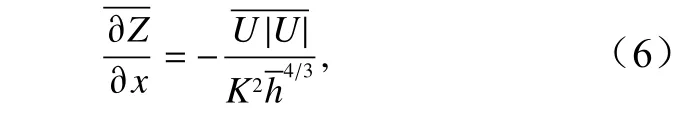
式中,上划线表示潮平均条件。径流影响下的潮波传播解析模型采用切比雪夫多项式(Chebyshev polynomials)分解方法,将式(6)中非线性摩擦项的二次流速项进行线性化处理,即

式中,pi(i=0,1,2,3)为切比雪夫系数,可表示为α=ar ccos(−φ)的 函数(其中φ=Ur/υ 表示无量纲径流参数):

基于式(7),径流影响下的潮波传播解析解可通过求解包含以下4 个非线性方程的方程组(涉及潮波振幅梯度、流速振幅、波速和相位差)得到[14]:
波速方程:

式中,λ=c0/c为波速参数,其中c0为无摩擦棱柱形河口的潮波传播速度,c为实际潮波传播速度;δ为潮波衰减或增大参数;为河口形状参数,
相位方程:

式中,ε=π/2−(ΦA−ΦV)为高潮位和高潮憩流(或低潮位和低潮憩流)之间的相位差,其中ΦA和ΦV分别表示水位和流速的相位。
尺度方程:

式中,µ=υ/(rsζc0)为流速振幅参数(可用于求解潮波流速的振幅 υ),其中rs=Bs/B为边滩系数(Bs为满槽河道宽度),ζ=η/为无量纲的潮波振幅。
潮波衰减/增大方程:

式中,χ=rsgc0ζ[1−(4ζ/3)2]−1/(ωK2h)为摩擦参数;θ、β以及Γ表征河流流量的影响,其表达式分别为
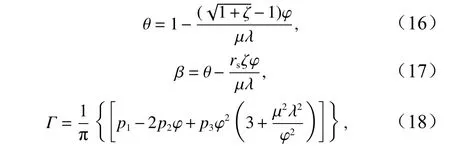
由式(12)至式(15)组成的隐函数方程组不能直接得到显式解,其解析解需要通过迭代算法取得。通过将河道分为多个河段(如间隔1 km),采用线性积分形式,沿程逐一计算潮波特征参数,逐步向上游方向求解得到沿程的余水位。
对于径流控制为主的河段,潮汐影响可忽略不计。此时,断面平均流速U与径流流速Ur等值反向,即将上式代入式(6)并结合式(1)和式(2),可得无潮汐影响下余水位梯度的解析表达式:

为了更好得表征上游流量Q和外海边界振幅η0的大小,便于比较不同河口的流量和外海边界振幅的差异,本文引入无量纲化流量参数τ0和外海边界振幅参数ζ0:

式中,Qr0为无潮汐影响下外海边界处断面的均衡流量,可由得到,其中hr0为无潮汐影响下外海边界处的实际水深。
3.3 余水位梯度的解析分解
将式(7)代入式(6),可将余水位梯度分解成3 个部分,代表控制余水位梯度变化的3 个主要动力因子[14]:径流动力因子:

潮动力因子:

径潮相互作用因子:

对分解得到的余水位梯度fr、ft、ftr分别积分,可得径流因子、潮流因子以及径潮相互作用因子控制形成的余水位。
3.4 潮区界和回水界位置的界定方法
潮区界的概念最早始于前苏联学者萨摩伊洛夫,他认为“河口区上界(即潮区界)为水位变化受潮汐或增水影响刚好消失的断面”[25]。潮区界位于潮流界的上游方向,是受潮汐波动影响的河流上游的最远点。该界面以下河段,径流受潮流顶托,水位随着潮汐的涨落而升降,直到界面处潮差趋近于0。该界面以上河段,水位虽不再受潮汐波动的影响,但水位相比于无潮情况下的水位,仍受到潮流的顶托而有所抬升,这种水位抬升的上界即为本文定义的回水区上游界限—回水界。本文定义的回水界与Lamb 等[5]关注的仅考虑径流影响下水面线形态变化的回水长度理论不同,聚焦潮汐引起的水位增幅,并以回水界作为河口区潮汐影响的最远点。
潮区界可由潮波振幅η趋近于0 的位置进行确定[26]。类比潮区界位置的界定方法,本文以沿程潮平均水深进行无量纲化,将受潮流顶托增长的水位(即受潮汐影响下余水位减去无潮汐影响下余水位)与潮平均水深的比值等于某一恒定值的位置,确定为受潮汐影响下河口区回水界的位置。河口区内潮区界ζ和回水界ξ位置的界定表达式分别由下式给出:

4 结果分析
4.1 解析模型的率定
基于2007 年实测的长江河口地形,构建数字高程模型(DEM),提取河口沿程的平均河宽B和断面平均底床高程Zb(均相对于1985 国家高程基准),并采用式(1)和式(2)拟合解析模型所用的地形特征参数,结果如图2 所示。由图2b 可见,从天生港至大通,长江河口主干河道沿程水深(相对于1985 国家高程基准)总体呈减小趋势,平均水深为10.86 m,最大水深为25.17 m。曲线拟合结果可得形态参数Br=2 005 m、B0=6 735 m、b=44 km、Zb0=–14.06 m、s=1.37×10−5。由于长江河口潮波性质以半日分潮为主,且解析模型仅能反演单一分潮的潮波传播情况,模型假设外海边界潮波周期与M2分潮一致,即12.42 h。模型假设边滩系数rs=1,因此解析模型仅需率定曼宁摩擦系数的倒数K。基于2003–2014 年长江河口沿程各站收集的水文数据,以大通站的月均流量和天生港站的月均外海边界振幅作为模型的上下游动力边界输入,计算得到江阴至芜湖5 个潮位站的潮波振幅和余水位,并与实测值进行对比(图3),用于率定K值,得到K=48 m1/3s−1。由图3 可见,模型计算值与实测值吻合较好(相关系数R2≥0.8),表明解析模型可较好地反演长江河口沿程一维径潮动力的主要变化。图3a 中江阴和镇江两个站点潮波振幅的计算值偏大,图3b 中芜湖和马鞍山两个站点余水位的计算值亦偏大,均与解析模型采用概化地形(如假设底床高程呈线性变化,忽略江心洲等影响)和简化水动力边界(如忽略M4、M6等浅水分潮影响)有关。

图2 长江河口平均河宽(a)和底床高程(b)的沿程变化及其曲线拟合Fig.2 Longitudinal variations of the tidally averaged channel width (a) and bed elevation (b) along the Changjiang River Estuary and their fitting curves
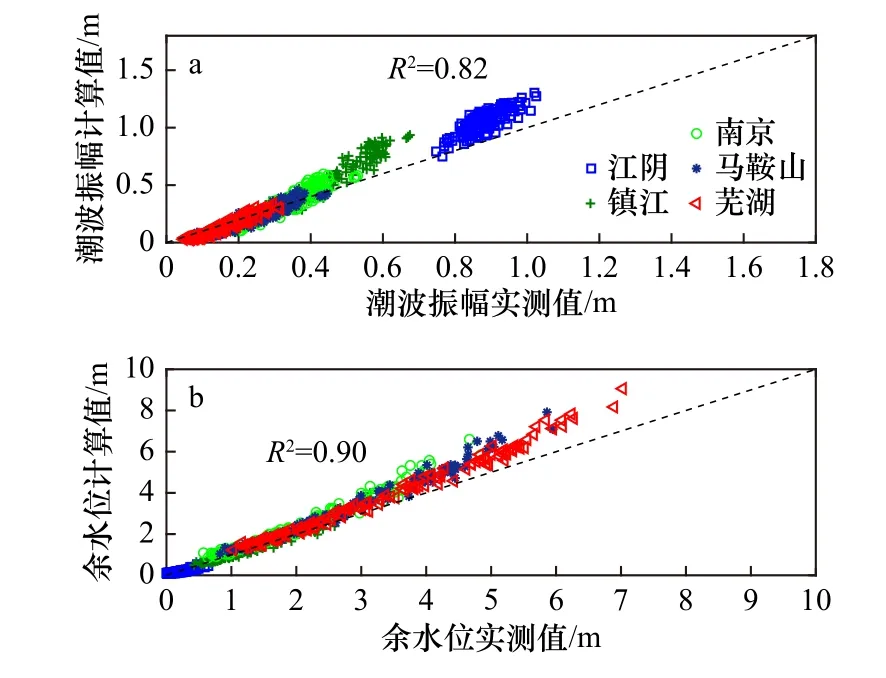
图3 实测潮波振幅(a)、余水位(b)与解析模型计算值的对比Fig.3 Comparison of the observed tidal amplitude (a) and residual water level (b) with analytically computed results
4.2 回水界位置对上游流量和外海边界振幅的响应
受潮汐影响的河口区回水界,其位置不仅具有显著的海洋潮汐大小潮周期性变化,亦具有明显的径流季节性变化。为探讨回水界位置对动力边界(即上游流量和外海边界振幅)的响应,基于率定验证后的解析模型,反演不同流量和振幅影响下回水界的空间变化,并与潮区界进行对比。解析模型以无量纲的流量参数τ0和外海边界振幅参数ζ0分别代表上下游动力边界,基于2003–2014 年长江河口天生港潮位站逐日潮波振幅与大通水文站日均流量的实测资料,取ζ0的变化范围为0.05~0.15,τ0的变化范围为0.1~0.8。模型计算区域为1 000 km,结果如图4 所示,其中红色实线代表回水界或潮区界的位置(即ξ=0.01 或ζ=0.01)。由图4a 至图4c 可见,不同径潮动力组合条件下,解析模型计算得到的回水界参数ξ一般先沿程增大至极大值,之后缓慢减小直到为0,因此回水界指标(即ξ=0.01)所对应的位置有2 个,靠近上游的位置为真实的回水界(即图4a 至图4c 中黑色虚线右边所对应的结果)。在高流量和低振幅条件下,回水界参数ξ沿程均小于式(26)定义的回水界指标(即ξ=0.01)。此时径流影响远强于潮汐影响,模型可简化为仅受径流动力影响的回水模型,河道沿程余水位即为无潮汐影响下的余水位。黑色虚线对应的红色实线极值点代表该外海边界振幅条件下离天生港最近的回水界位置(即最小回水长度)。当外海边界振幅参数ζ0=0.05、0.1、0.15 时,红色实线极值点对应的临界流量参数τ0为0.27、0.55、0.82,距天生港的距离分别为155 km、85 km、62 km,表明潮汐动力越强,红色实线极值点对应的临界流量越大,距天生港的距离也越小。

图4 不同径潮动力组合条件下回水界参数ξ(a–c)和潮区界参数ζ(d–f)的沿程变化等值线图Fig.4 Contour plots of longitudinal variations of parameters of backwater limit ξ(a–c) and tidal limit ζ (d–f) under different tide-river conditions
由图4a 至图4c 亦可见,回水界距天生港的距离与上游流量、外海边界振幅密切相关,分别具有显著的负相关和正相关关系,即流量越大,回水界离天生港越近,外海边界振幅越大则反之。图4d 至图4f 为潮区界参数ζ在不同径潮动力组合条件下的空间变化。由图4 可见,潮区界位于回水界下游方向,两者之间的距离随着流量的增大而减小,随着外海边界振幅的增大而增大。潮区界位置对上游流量和外海边界振幅的响应规律,与回水界基本一致。与潮区界相比,回水界位置对径潮动力的响应更为敏感,这表明回水界是表征河口感潮河段径潮动力格局演变的有效切入点。
为进一步定量分析长江河口回水界对上游流量和外海边界振幅的响应过程,使用解析模型计算不同径潮动力组合条件下回水界距天生港的距离,结果如图5 所示,其中左上角的空白部分对应高流量、低振幅的输入条件,表明潮汐引起的回水效应基本可忽略。由图5 可见,回水界距天生港的距离(即回水区长度,单位:km)Lb与流量参数τ0、外海边界振幅参数ζ0存在明显的线性关系,可进一步对计算结果进行二元一次线性拟合,得到它们之间的定量关系为Lb=722.1−1 948τ0+3 745ζ0,相关系数R2=0.92。

图5 不同径潮动力组合条件下回水界距天生港距离的等值线图Fig.5 Contour plot of distance from Tianshenggang to backwater limit under different tide-river conditions
4.3 长江河口回水界的季节性变化特征
基于率定验证后的解析模型,反演2003–2014 年长江河口逐月的回水界时空变化特征,结果如图6 所示。由图6 可见,长江河口回水界距天生港的距离具有明显的季节性变化特征,与月均流量呈现明显的负相关关系,即流量越小,回水界离天生港越远,反之则越近。月均流量最小的1、2 月份,其回水界离天生港最远,可达940 km。月均流量最大的7 月份,回水界参数ξ沿程均小于式(26)定义的回水界指标(即ξ=0.01),表明河口沿程基本不受潮汐影响。由图6 亦可见,长江河口回水界距天生港的距离在1 年内的极大值和月均外海边界振幅呈现明显的正相关关系,但由于本文采用月均数据,回水界主要呈现显著的季节性变化特征。

图6 长江河口月均流量及外海边界振幅变化(a)及对应条件下回水界参数ξ 的时空变化等值线(b)Fig.6 Variations of monthly averaged discharge and tidal amplitude of seaward boundary (a) and contour plot of spatial-temporal variation of the backwater limit ξ under the corresponding conditions (b) in the Changjiang River Estuary
以长江河口2003–2014 年春夏秋冬4 个季节流量及外海边界振幅的多年平均值作为模型的动力边界输入,聚焦感潮河段区域(500 km 以内),从季节尺度分析回水界的季节性变化特征,其余水位及参数ξ的沿程变化如图7 所示。由图7 可见,夏季由于流量较大,余水位明显大于其他季节,其参数ξ沿程均小于式(26)定义的回水界指标(即ξ=0.01),潮汐引起的回水效应基本可忽略;春季和秋季流量相近,回水界位于芜湖附近(春季Lb=419 km、秋季Lb=367 km);冬季流量最小,感潮河段区域内未能显现其回水界,即潮汐影响范围大于500 km。

图7 不同季节长江河口余水位及回水界参数ξ 的沿程变化Fig.7 Longitudinal variations of the residual water level and the parameter of backwater limit ξ in the Changjiang River Estuary in different seasons
5 讨论
根据式(26)定义的回水界,可知Z(受潮汐影响下的余水位)与(无潮汐影响下的余水位)是决定回水界的关键参数。通过切比雪夫多项式分解方法,Z可分解为径流因子fr积分的余水位、潮流因子ft积分的余水位以及径潮相互作用因子ftr积分的余水位3 部分,且理论上等于仅受径流影响下的余水位。当潮波流速振幅和径流流速相平衡时(即φ=1),的梯度表达式与的梯度表达式相同,即。因此,本文假设与沿程相等,则回水界的位置主要取决于潮流因子和径潮相互作用因子的变化。
图8 显示不同季节长江河口余水位梯度分解项ft(潮流因子)和ftr(径潮相互作用因子)的沿程变化。由图8 可见,除夏季外,长江河口各个季节ft和ftr沿程均先增大后减小,ftr的峰值位置相比ft更接近天生港,且冬季离天生港最远,夏季离天生港最近,这与回水界的季节变化特征一致。峰值过后,各个季节ft沿程减小逐渐趋近于0,ftr则沿程减小直至潮波流速振幅和径流流速相平衡(即φ=1)的位置等于0。图9显示不同季节长江河口余水位分解项及其占总余水位比值的沿程变化。由图9 可见,由于余水位梯度分解项ft和ftr对余水位的影响具有累积效应,两者积分的总水位将趋近一恒定值直到上游边界,理论上由潮汐引起的回水效应亦会持续到上游边界。越靠近上游边界,径流的影响越强烈,因此占总余水位的比值会逐渐减小。本文定义的回水界,其核心是对潮流因子和径潮相互作用因子影响程度的一种界定,当以上两个因子的影响小到一定程度时,可认为潮汐引起的回水基本消失。

图8 不同季节长江河口余水位梯度分解项ft 和ftr 的沿程变化Fig.8 Longitudinal variations of ft and ftr derived from the residual water level slope in the Changjiang River Estuary in different seasons

图9 不同季节长江河口余水位分解项及其占比的沿程变化Fig.9 Longitudinal variations of derived from the residual water level and its contribution in the Changjiang River Estuary in different seasons
6 结论
本文在经典河流回水理论的基础上考虑潮汐动力的影响,聚焦潮汐动力引起的回水效应问题,基于径潮动力耦合驱动的一维水动力解析模型,重新定义河口回水区上游界限(回水界),并提出相应的界定方法。通过给定不同径潮动力组合条件,探讨回水界位置对上游流量和外海边界振幅的响应过程,并以长江河口为例,探讨该河口回水界的季节性变化特征及影响机制。主要结论如下:
(1)回水界距天生港的距离与上游流量、外海边界振幅分别具有显著的负相关和正相关关系,且基本为线性关系。基于长江河口2003–2014 年的月均流量和潮波振幅资料,计算得到回水界距天生港的距离(即回水区长度)Lb与无量纲上游流量参数τ0、外海边界振幅参数ζ0的定量关系为Lb=722.1−1 948τ0+3 745ζ0。与潮区界相比,回水界对径潮动力的响应更为敏感,是表征河口感潮河段径潮动力格局演变的有效切入点。
(2)长江河口回水界距天生港的距离具有显著的季节性变化特征,且与月均流量呈现明显的负相关关系。聚焦感潮河段区域(500 km 以内),长江河口夏季潮汐引起的回水效应基本可忽略,春季和秋季回水界位于芜湖附近(春季和秋季分别距天生港419 km和367 km),冬季回水界位于感潮河段以上区域。
(3)回水界定义的核心是潮流因子和径潮相互作用因子对余水位形成影响程度的界定,代表河口潮汐影响的最远点。长江河口潮流因子和径潮相互作用因子控制的余水位梯度季节性变化显著,是长江河口回水界位置季节性变动的主导因素。
