基于Morlet小波变换的层序识别方法——以冀东油田高浅南区59-35断块为例
2022-02-03冯建松朱春艳轩玲玲刘晓彤汪义莉
冯建松,李 涛,朱春艳,轩玲玲,周 微,刘晓彤,汪义莉
基于Morlet小波变换的层序识别方法——以冀东油田高浅南区59-35断块为例
冯建松1,2,李 涛2,朱春艳2,轩玲玲2,周 微2,刘晓彤2,汪义莉1
(1.油气资源与勘探技术教育部重点实验室(长江大学),武汉 430199;2.中国石油冀东油田分公司陆上油田作业区,河北 唐山 063299)
快速准确识别层序地层界面对于地层的划分与对比非常重要,因此,如何利用测井曲线资料对层序进行快速分析处理具有重要的应用价值。本文在小波变换理论的基础之上,提出了一套自动划分、对比层序地层单元的方法。采用归一化最大能谱法确定最优尺度,利用最优尺度对应的小波系数识别层序地层单元,实现了利用GR测井曲线对层序地层单元进行自动划分。另外,通过分析Morlet和Mexihat小波基之间的差异,对比地层单元典型井的沉积特征,得出采用Morlet小波基划分地层后的分割结果更准确和稳定,更适合于序列的地层单元划分。最后,利用动态波形匹配算法,提取自动划分的层序地层单元测井曲线特征参数,通过特征参数匹配,实现层序地层单元对比。该方法对同类油田的层序识别具有一定的推广意义,对改进地质研究流程也具有促进作用。
小波变换;Morlet小波;层序界面;沉积旋回;地层对比
利用小波变换分析处理地球物理信息是十分有效的。它可以从更微观的角度深入了解某些地质现象的内部情况,进而揭示地质现象演化过程的本质。近些年来,小波变换在发展过程中逐步引入了多尺度分析的思想(Daubechies I, 1992),在此思想基础上,可以在一定程度上将信号分析的时频局部化,而且媲美人工逐级分层解释的方法(操应长等,2003;陈锡民等,1998)。利用这种引入了多尺度分析思想的小波变换手段,可以将提取地层的时频特征变得更加方便且准确(陈一鸣等,1990;胡吕华等,2004;黄捍东等,1999),进而有助于获得层序旋回等相关地质信息。

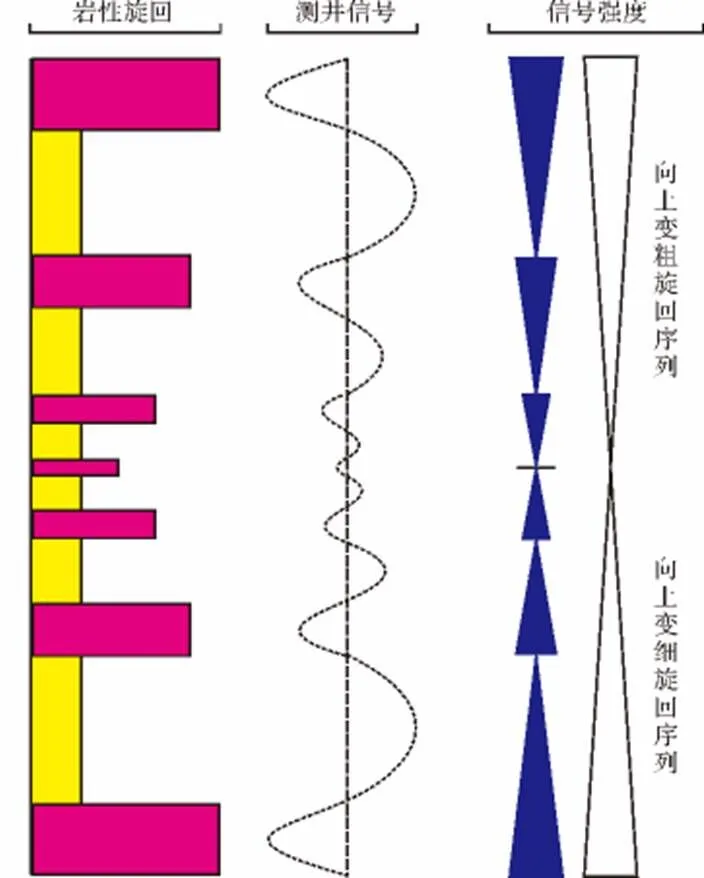
图1 测井信号与岩性旋回关系
针对此类问题,本研究从测井信号特征出发,充分结合小波变换分析方法和多尺度分析思想,实现了研究区不同尺度层序地层单元的定量划分与对比,并在此基础上,建立研究区层序地层单元格架。
1 小波变换识别层序的理论基础
通常在我们所研究的沉积岩地层中,沉积物的变化特征能反映出沉积当时的水体变化特点。随着沉积时水体的不断加深,沉积物会随之发生相应的变化,比如沉积物中有机质和放射性物质的含量,以及各种微量元素的变化等,即地层中沉积物随水深变化的旋回特征可以在测井曲线上间接反映出来,而小波变换可以将测井曲线上的一维深度域信息转为包含深度和频率的二维域信息,而且小波分析具有多尺度分析功能,可以在测井曲线中识别不同频率的曲线旋回,进而反映出不同周期的沉积旋回。具体来说,高频率的沉积旋回与高频率的曲线旋回相对应,低频率的沉积旋回与低频率的曲线旋回相对应。因此,针对不同级别的层序单元,不同周期的沉积旋回可以用不同频率的测井曲线旋回划分(图2)。
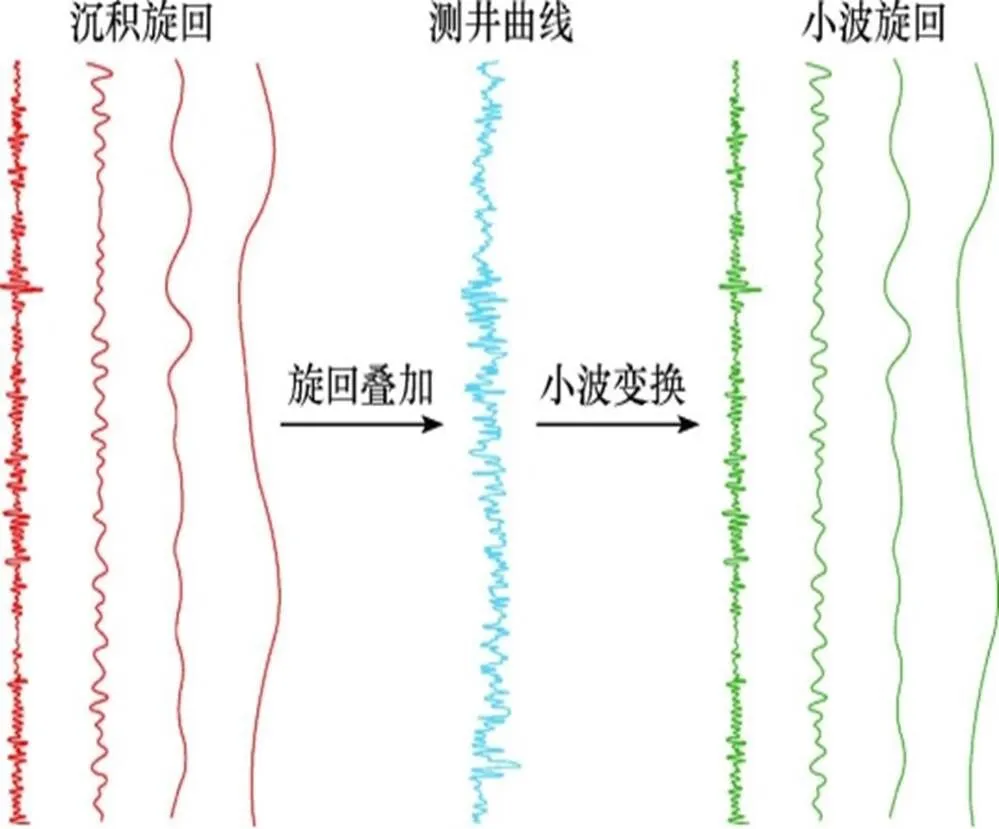
图2 小波分析识别沉积旋回理论示意图
2 小波变换
2.1 原理
函数的伸缩、平移是小波变换的基本思想,具体是定义某一种小波函数为Ψ(t),然后将小波函数Ψ(t)的自变量t进行伸缩a与平移b,经过处理后,再与待变换的函数X(t)作内积(李霞,2007;焦翠华等,1999),进而得到函数WTX(a,b),如式(1)。
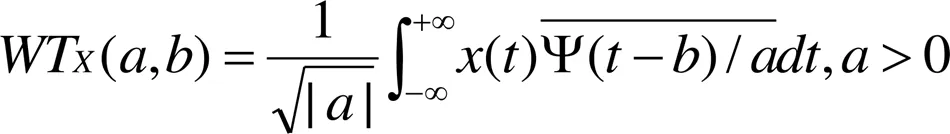
通常来说,小波函数Ψ(t)具有有限支撑集,即Ψ(t)在的一个有限集合之外全部等于0。基本小波或小波母函数定义为:
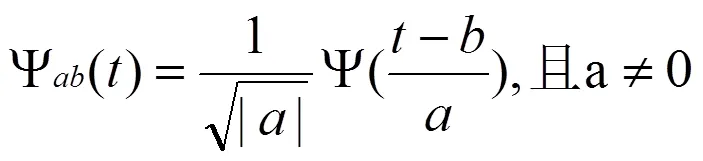
小波变换系数值是位移因子与尺度因子的函数,小波系数的数值大小揭示了小波函数与测井信号的相似程度,可理解为要分析的测井信号与小波的协方差选用小波对测井数据进行连续小波变换后,得出一系列与尺度和深度相对应的小波变换系数值。其地质学意义在于由多个不同周期尺度沉积旋回叠加的测井曲线,通过小波变换,被分解成各自周期独立的沉积旋回,以尺度的形式展示出来(李霞等,2006;陈正星,1998;吴伟龙,2011)。式(2)中的a为尺度变量,其大小程度决定了测井信号的采样窗长;b为位移变量,其大小程度决定了接近测井信号的时间位置。另外,频率和小波的尺度密切相关:如果小波的尺度变量a的值越小,此时小波表现为被压缩状态,则在时间轴上的观察范围变得相对变小,这与测井信号的高频分量相对应,所以,就可以使用高频的小波进行微观尺度的观察,也表明该时期的沉积周期短,与之对应的地层旋回厚度小,可划分准层序;如果小波的尺度变量a越大,此时小波表现为被拉伸状态,则在时间轴上的观察范围相对变得更大,这与测井信号的低频分量相对应,因此,低频小波可以用于宏观观察,这也表明该时期的沉积期长,对应的地层旋回厚度大,可用于层序或准层序的划分。
2.2 测井曲线的选择
地层中天然伽马射线的强度不都是相同的,其强度取决于地层中各种不同的放射性物质的含量,自然伽马测井就是用来测量这种天然伽马射线的强度。泥质含量的大小决定了地层中岩石的自然伽马射线强度,原因在于黏土颗粒较强的吸附能力,与其他的骨架颗粒相比,黏土颗粒吸附放射性元素的能力要强。根据自然伽马测井曲线特性,其在划分碳酸盐岩、碎屑岩剖面、富含泥质地层时显示为高值。富含放射性元素(如钾长石、云母等)的岩层会显示出异常的高值,当选取对比标志层时,就会优先选取这类岩层。利用其进行层序界面划分与地层对比具有明显的优势,也是最有效的方法。因此,本次分析利用自然伽马测井曲线,在经过连续的一系列的一维小波变换后,通过考察多种伸缩尺度下小波系数的傅立叶级数展开频谱占据整个频带内总能量的比例最大的尺度,能检测到不同的频率段之间的突变情况,包括突变点或者突变区域,在地质问题上反映出来就是其形成环境的突变。各级层序界面的建立与这种曲线所表现出的明显的周期性振荡特征具有一定的对应关系,据此可以当做层序地层识别与划分的依据。
2.3 小波基的选取
Mexihat小波作为高斯函数的二阶导数,其在实际处理测井曲线时,选用Mexihat作为小波基,拥有以下优点:首先,测井曲线的形状与Mexihat小波的形状很类似,这样一来,在进行小波变换时可以最大程度的突出测井信号;其次,Mexihat小波作为Bubble子波的特殊小波,但是Bubble函数是一种曲线形态比较光滑的函数,对单独的某个噪声点的反应不是很强烈,然而其表现在时域侧方面的抑制属性,能够对测井信号进行夸张化,特别突出信号中重要的快变特征信息。由于Mexihat小波是高斯函数的二阶导数,在进行小波变换时可以充分利用它可积的特性,有利于算法的快速实现。因此,此次在进行小波变换时,初步选用了Mexihat作为小波基。
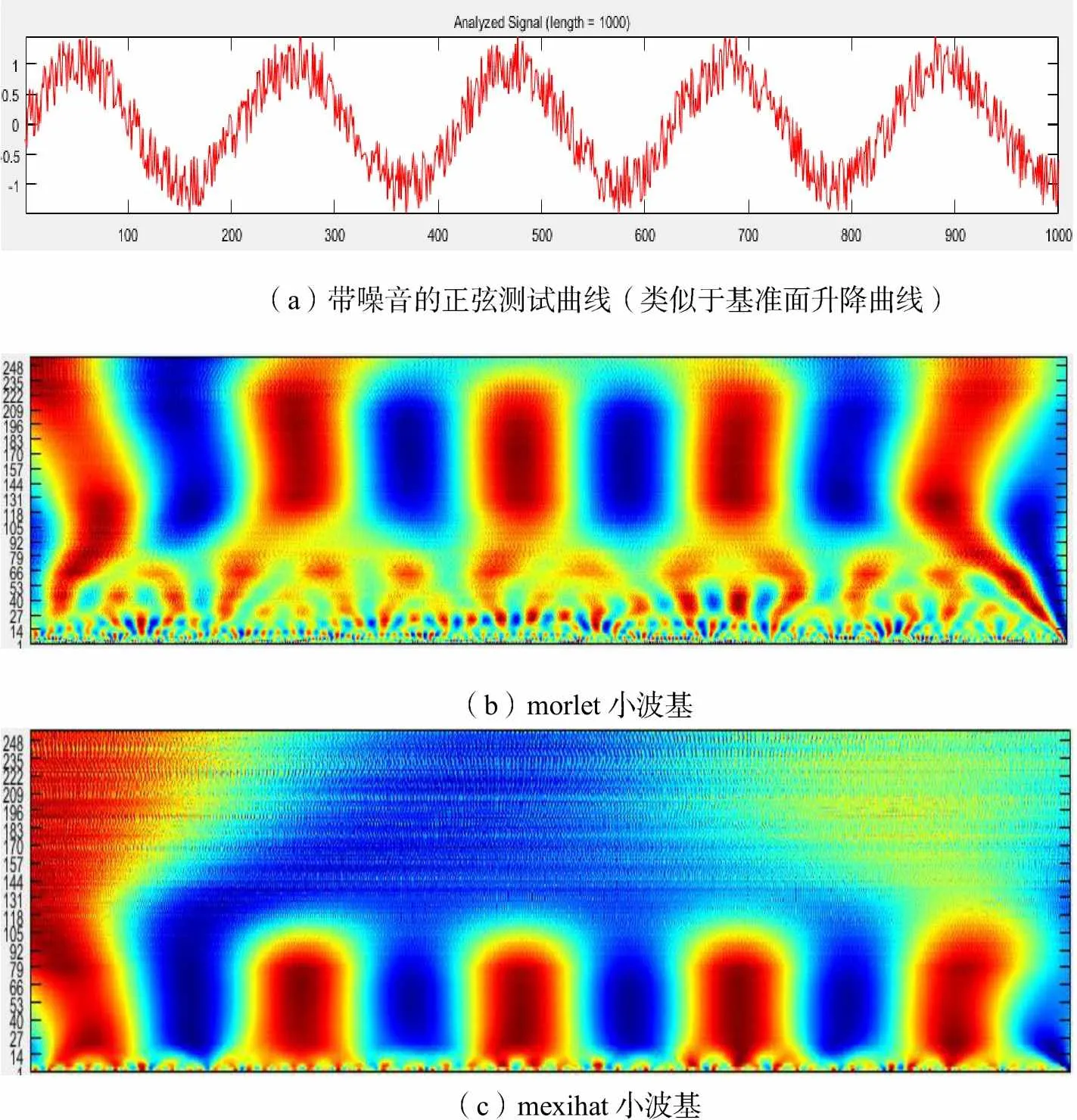
(a)带噪音的正弦测试曲线(类似于基准面升降曲线) (b)morlet小波基 (c)mexihat小波基
由于小波母函数是Morlet小波,它是一种复值小波,在一定程度上能够较准确地提取信号中的幅度及其变化值和有关相位的一些信息。基于Morlet小波的这种优点,在地球物理中广泛应用这种小波进行信号的相关处理。除此之外,Morlet小波也是一个周期函数,在识别不同级别层序单元界面时,先将需要融合的测井曲线进行小波变换,在此基础上求出小波系数,进而生成的小波系数能量图谱,能量团中心点对应下降半旋回顶界面,以此为旋回分界点,图5中旋回C界面顶部即为旋回分界面,该界面处也是沉积环境能量最强的时期,然后在两个分界点内部以小波系数曲线的极值点和形态划分出半旋回。根据时频色谱图所反映的宏观概貌信息显示,即在同一时期沉积形成的地层表现为同一尺度上的颜色相同,再使用归一化最大谱能量法确定最佳尺度因子(张贤达等,1998),然后提取最佳尺度因子所对应的小波系数。在将测井曲线进行多尺度分解之后,同一尺度内周期内的小波系数呈现出相似的振荡趋势,按照从大到小的顺序,在宏观尺度上识别出界面层序,依据层序内部特征识别各类型准层序组界面,进而依次从各类型的准层序组内部分辨出各准层序界面。需要说明的是在利用小波系数曲线识别准层序组界面时,旋回类型参照小波系数曲线的形态进行判断的方法:按照由下至上的原则,小波系数曲线由波峰—波谷(小波系数值减小的过程)的反粒序变化,代表反半旋回沉积,小波系数曲线由波谷—波峰(小波系数值增大的过程)的正粒序变化,代表反正旋回沉积。参照最佳尺度下的小波系数曲线的峰值位置和变化趋势以达到准确划分不同级别层序单元界面以及旋回类型的目地。选用对岩性反映敏感的GR曲线做小波分析(图3a),测试曲线时频谱中识别2种频率成分(图3b、3c),应用分辨率较高的morlet小波基。基于此,本次拟采用Morlet小波变换进行层序的识别与划分研究。
(a) (b)
3 基于Morlet小波变换的层序识别研究实例
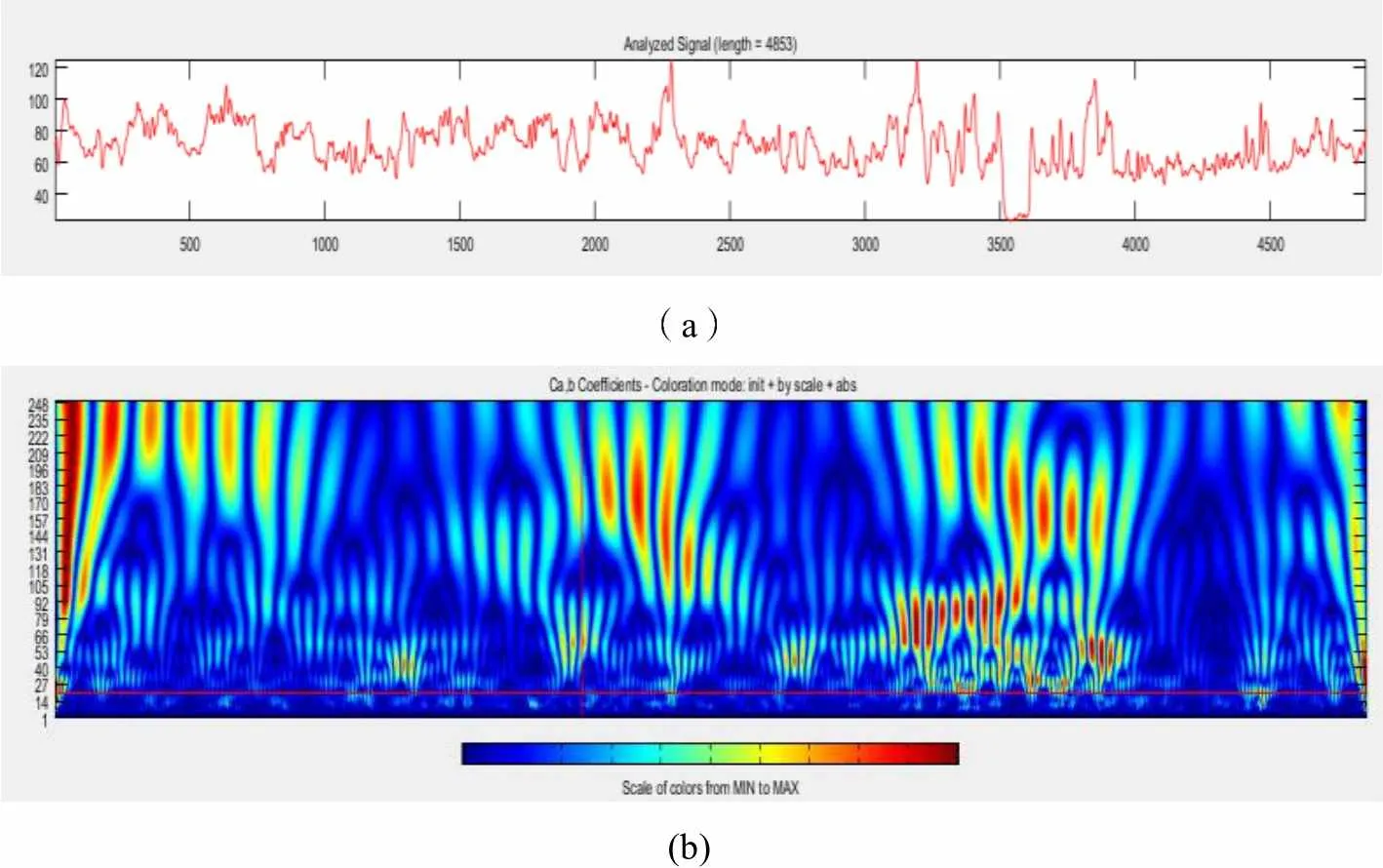
高尚堡油田位于南堡凹陷北部、西南庄和柏各庄断层的下降盘。该油田高南浅层构造是一个受高柳断层作用形成的被断层复杂化的逆牵引背斜构造。本次研究选取高尚堡油田高浅南区高G59-35断块明化镇-馆陶组进行研究。研究井62-35井段深度为1540~2130m,采样间隔为0.125m。由于62-35井该深度井段属于曲流河沉积,属于“泥包砂”,由于季节性的水流使得该井段为大段泥岩和大段砂岩交互出现,表现出明显的水平面深浅变化,易于进行旋回的划分。此次重点对高59-35块NmⅢ~NgⅣ油组地层开展小波变换,通过多尺度因子与各级层序旋回的匹配度进行分析。连续小波变换过程中包含的重要参数为尺度因子,不同尺度因子对应小波变换时提取的原始信号高低频信号比例。尺度因子越大,小波系数的频率越低,越能反映测井曲线中的大尺度沉积信息。经过多次试验,本次选取最优尺度因子分别为110、50、30,分别对应于高分辨层序的长期旋回、中期旋回、短期旋回。
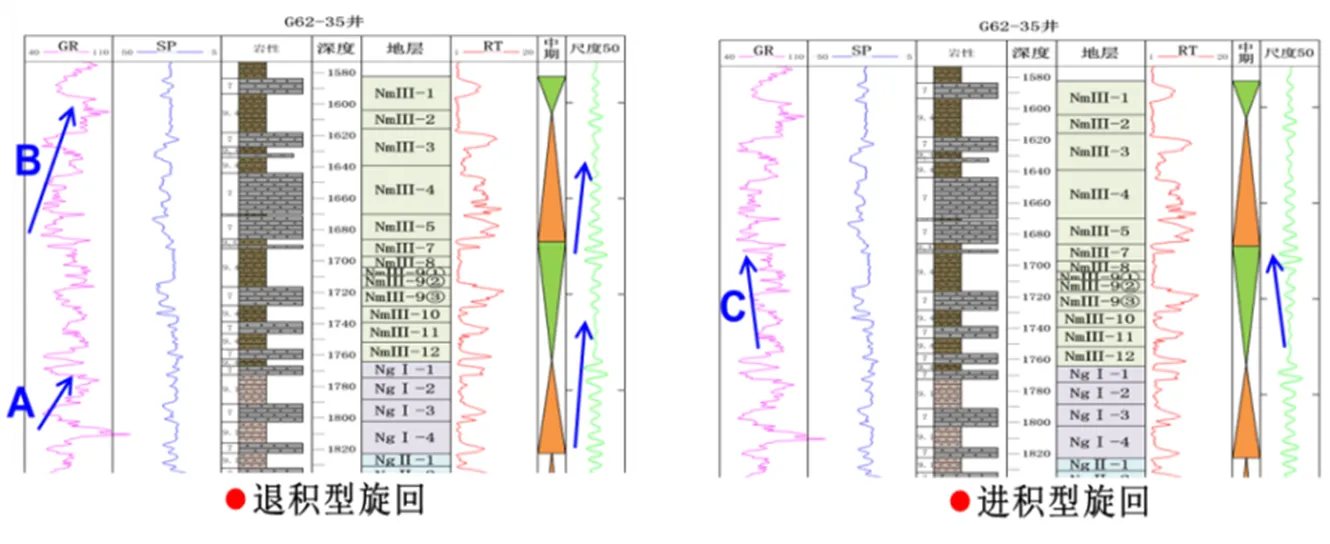
图4(a)为原始的自然伽马测井曲线,纵坐标为自然伽马的测井值;横坐标表示测量深度,从左向右表示深度逐渐增加。
图4(b)利用Morlet连续小波变换方法处理后的自然伽马测井曲线,其生成的小波系数时频色谱图,颜色的亮度与小波值呈正比,随着颜色的明暗变化,其小波系数呈现相应的变化,横坐标为深度位移变量b,纵坐标代表尺度变量a。再经过小波变换处理后,可以从图中明显观察到,测井曲线已经从一维深度函数转换成二维空间深度—尺度的函数,并且尺度和深度的不同代表着周期性的差异。通过综合观察小波系数时频色谱图,大致可以认为在图中颜色较亮的大尺度位置上发育大规模的沉积旋回界面,即层序或准层序组,并且在这种大规模的沉积旋回内部,还夹杂着若干个不同规模尺度的小沉积旋回(准层序)。图中尺度变量因子在100~120范围内,主要以大规模沉积旋回为代表,可用于准层序的识别。小尺度沉积旋回的规模范围为40~70个左右,可用于准等序单元的识别。尺度在50以下可认为与高频地层旋回岩层组或岩层相对应。
能量群反映了地层沉积物粒度和水动力条件的变化。箭头指向湖泛面小波系数曲线峰谷交界(能量团强弱转换),可作为地层突变界面,反映沉积环境变化,亦可作为层序界面。退积型旋回小波系数震荡幅度向上减弱,时频谱图能量团逐渐减小,进积型旋回小波系数震荡幅度向上增强,时频谱图能量团逐渐增大(图5)。
在选定的最佳尺度下,以能谱图中能量团中心点作为分界点,根据小波系数曲线周期性振荡趋势特征,在尺度a=50时划分出2个准层序组;在尺度a=30时在准层序组内部更细致的划分出4个准层序,层序划分结果如图6。
4 结论
实践和研究分析表明,测井曲线蕴含着许多复杂且丰富的地质信息,单纯依据测井曲线进行层序地层的识别与划分具有一定的局限性,而通过Morlet小波变换的分析方法,能够克服原始测井曲线信号中固有的复杂多变性,进而较准确地识别和提取出测井信号的时频特征。利用该方法,将自然伽马测井曲线作Morlet连续小波变换处理后,可以将一维的原始测井数据拓展到同时具有深度和尺度的二维空间。
通过多尺度因子与各级层序旋回匹配度的分析,综合选择最优尺度因子后,根据小波系数曲线在最优尺度上的周期振荡原理,可以更准确地识别和划分不同层次的各层序地层单元。如层序、准层序和准层序组等。而且,该方法能有效避免不同的科研工作者的主观因素干扰,在一定程度上有弥补了传统研究方法存在的缺陷。

图6 G62-35井Morlet小波识别划分层序地层单元示意图
操应长,姜在兴,夏斌,王居峰,杨伟利,王卫红.2003.利用测井资料识别层序地层界面的几种方法[J].石油大学学报(自然科学版),(02):23-26.
陈锡民,徐文立,夏凯.1998.基于地层一致性检验的测井信号地层自动对比算法[J].石油地球物理勘探,(06):775-781.
陈一鸣,王向公,刘子云.1990.利用有序元素的最佳匹配法进行地层对比[J].江汉石油学院学报,1990(01):33-39.
胡吕华,李国华,刘涛.2004.MALAB6.X的系统分析与设计——小波分析[M].西安:西安电子科技大学出版.
黄捍东,胡光岷,贺振华,黄德济.1999.测井约束多尺度储层厚度反演[J].成都理工学院学报,(04):343-347.
李霞.2007.测井多尺度分析方法在层序地层分析中的应用研究[D].中国石油大学.
焦翠华,李冰.1999.零通小波用于测井曲线多尺度分层[J].测井技术,(03):13-15.
李霞,范宜仁,邓少贵,房文静.2006.利用测井资料研究层序的方法述评[J].测井技术,(05):411-415.
陈正星.1998.小波分析算法与应用[M].西安:西安交通大学出版社.
吴伟龙.2011.基于小波变换的地震信号瞬时参数提取方法研究.[D].东北石油大学.
张贤达,保铮.1998.非平稳信号分析与处理[M].北京:国防工业出版社.
Sequence Identification Method Based on MorletWavelet Transform——Taking High-Shallow South 59-35 Fault Block in Gaoqiannan Area as an Example
FENG Jian-song1,2LI-Tao2ZHU Chu-yan2XUAN Ling-ling2ZHOU Wei2LIU Xiao-tong2WANG Yi-li1
(1-Key Laboratory of Oil and Gas Resources and Exploration Technology of Ministry of Education (Yangtze University), Wuhan, Hubei 430058;2-PetroChina Jidong Oilfield Branch Company's onshore oilfield operation area, Tangshan, Hebei 063299)
Rapid and accurate identification of sequence stratigraphic interface is very important for stratigraphic division and correlation. It is of great application value to analyze sequence quickly by using logging data. Based on the wavelet transform theory, this paper presents the automatic division of sequence stratigraphic units by using GR logging curve, puts forward a set of automatic division and correlation methods of sequence stratigraphic units, determines the best scale by using the normalized maximum spectral energy method, and uses the wavelet coefficient corresponding to the best scale to divide sequence stratigraphic units. Additionly, through the comparative analysis of the sequence stratigraphic unit division results of the three typical sedimentary characteristic well sections by Morlet and Mexihat wavelet, it is concluded that the Morlet division result is more accurate and the performance is relatively stable, which is more suitable for the division of sequence stratigraphic units. Finally, the dynamic waveform matching algorithm is used to extract the automatically divided log characteristic parameters of sequence stratigraphic units. Through the matching of characteristic parameters, the correlation of sequence stratigraphic units is realized. This method has a certain extension significance to the sequence identification of similar oil fields, and also promotes the improvement of geological research process.
wavelet transform; Morlet wavelet; sequence interface; sedimentary cycle; stratigraphic correlation.
P631.4
A
1006-0995(2022)04-0713-05
10.3969/j.issn.1006-0995.2022.04.033
2021-09-22
页岩油气富集机理与高效开发国家重点实验室开放基金“GSYKY-B09-33”
冯建松(1980— ),男,山东济宁人,工程师,研究方向:油藏精细描述
汪义莉(1996— ),女,陕西安康人,硕士研究生,研究方向:开发地质
