基于三维重构的原岩硬性结构面抗剪强度

周玉鹿， 袁维*， 徐江， 王安礼， 王伟

(1.石家庄铁道大学土木工程学院， 石家庄 050043； 2. 贵州省水利水电勘测设计研究院有限公司， 贵阳 550002)

岩石的破裂形成不同的裂隙和破裂面，进而岩石内部产生各种纵横不规则的结构面；节理面就是其中最为重要的破裂面。由于节理面的形成，会导致岩石的力学性能发生很大变化；岩体的力学行为很大程度上受到节理面形貌特征的影响[1]。因此，将节理面的力学性质、各向异性以及破坏形式等协同起来进行统一研究，有利于进一步深入了解岩石节理面的抗剪力学特性。

目前，国内外众多学者对岩石节理面主要是从尺寸效应、各向异性等方面分割开来研究，通过表征节理面的行貌参数，进而建立峰值剪切强度准则[2-4]，节理面的形貌特征影响上、下节理面岩石的接触形式，以致影响岩石的抗剪强度。Patton[5]研究表明，通过研究齿状节理面试件的剪切强度，建立了符合摩尔-库伦公式的双线性强度准则表达式。为后续其他学者研究提供依据。

用以表征岩石节理表面的形貌特征常用方法有粗糙度系数经验法、几何形态统计法和分形分析方法等。任红磊等[6]通过直剪试验及PFC2D数值模拟，探究不同法向应力作用下节理的几何特征对岩体力学性质的影响。Barton等[7-8]采用大量节理岩石进行剪切试验，给出10条用来评价粗糙度系数(joint roughness coefficient，JRC)的标准粗糙度剖面线。一些学者以Barton模型为基础，用几何形态分析方法描述真实节理剖面线的特征来建立方程[8-10]，其中Gao等[9]和Tse[10]基于典型节理剖面线讨论了粗糙度系数JRC与粗糙度参数一阶导数均方根Z2和结构函数(structure factor，SF)之间的相关联系，进而通过量化粗糙度系数JRC来评定节理面粗糙程度。Yuan等[11]对剖面线累积相对起伏幅度(coefficient of relative risk aversion，CRRA)和加权平均梯度(weighted average gradient，WAG)进行数字化处理，依据岩石节理的爬升和摩擦效应对抗剪强度的影响，提出一种无纲量的JRC评价指标。该研究方法定量描述节理粗糙度系数具有二维性。节理面的形貌特征应通过三维量化参数来表征，才能真实反映节理岩石抗剪强度变化特性，对实际的理论指导也更有意义。

对于节理面形貌的非接触测量方法，一直是近几十年来快速发展并普遍使用的新型方法。该方法通过软件可以得到节理岩石的三维模型。包括图像法[12-14]、三维激光扫描法[15-18]等。葛云峰等[12]通过模拟虚拟光源，采用图像分割技术来获取结构面的数字信息，提出用光亮面积百分比(bright area percentage，BAP)来评价三维粗糙度系数JRC3D的方法。该方法中得到BAP的值，由于确定入射角度受人为因素的影响，对于准确的BAP值仍需要进一步探究。Maerz等[14]采用图像分析微机，进行数字化处理，然后分离阴影边缘，从而计算粗糙度参数。由于光照的变化和图像处理会产生误差，使得出的计算结果与实际岩石节理面的粗糙度存在偏差。

三维激光扫描技术与3D打印技术的发展让节理岩石试验变得更加方便，过去很难实现相同节理面的剪切试验，现如今已经可以大量制作表面形貌相同且接近原岩节理面的剪切试样。扫描仪与3D打印机的精度完全可以用于岩石节理的实验研究，这种新方法有利于研究岩石力学行为[19-22]。熊祖强等[19]通过3D打印技术制作的试样与原始试样进行对比分析，证明了采用3D打印技术可以建立形貌完全相同的人工节理试样，这将为重复进行实验提供条件。胥勋辉等[22]利用三维激光扫描进行逆向重构自然岩石节理面，研究节理面形貌特征的各向异性对剪切力学特征的影响。

以上研究成果针对岩石节理面抗剪强度的研究方法和手段已非常充分，但是对于岩石节理面抗剪强度具有方向性的问题仍然需进一步探究。现通过几何统计函数来定量计算三维粗糙度系数，考虑岩石节理沿剪切方向的爬升和摩擦效应；并采用沿剪切方向接触面积有效系数值来描述不同剪切方向岩石节理抗剪强度的差异性。最后，基于不同剪切方向抗剪强度的差异性，建立含有三维形貌参数的抗剪强度新模型。

1 试验研究

1.1 试件制备

EinScan-Pro三维激光扫描仪(扫描速度10帧/s、像素131万)具有生成数据快、能重复进行扫描、使用简捷、精度高等优点。采用该扫描仪对三种不同粗糙度的岩石节理面进行三维激光扫描，如图1(a)、图1(b)所示，获取节理面形态的高精度点云数据，如图1(c)所示。针对不同层面，通过工程软件对自然节理面的表面形态进行逆向重构，截取每个节理面不同角度的相应范围作为打印区域，如图1(d)～图1(f)所示，导出并生成3D打印机识别的格式。通过3D打印技术，制作与自然岩石节理面相同形貌的粗糙节理面模板，如图1(g)、图1(h)所示。

图1 节理面逆向制作流程Fig.1 Reverse production process of joint surface

使用3D打印机可以复制多个粗糙度完全相同的岩石节理面模板，并与制备好的模具一同浇筑所需要的水泥砂浆试件。浇筑试件需要在模具表面涂一层薄薄的润滑油；同理3D打印机制作的节理面模板也需要进行适量的涂油；这样既能保证不改变原始节理面的粗糙度，又能使试件顺利脱模，保证试件的完整性，以方便后续试验。采用水∶灰∶砂=1∶2∶2.5的比例(选用32.5普通硅酸盐水泥和中细砂)通过节理面模板和模具进行浇筑水泥砂浆试块，浇筑相关节理面试块如图2所示。在标准条件下养护试件，28 d后进行直剪试验。每个不同粗糙度岩样制备5组，同时制备试样长×宽为10 cm×5 cm的岩石标准试件。根据单轴压缩试验测得人工节理试件的基本力学参数见表1。

表1 节理的基本力学参数Table 1 Basic mechanical parameters of joints

图2 浇筑相关节理面试块Fig.2 Pouring of relevant joint interview blocks

1.2 剪切仪器与试验步骤

剪切试验选用自主研发的加锚结构面锚固性能试验仪。该仪器能实现多功能岩体加载，结构简单，易于操作，进行试验时可控性高，能直观的显露岩石进行各种试验的破坏情况。加锚结构面锚固性能试验仪如图3所示。

图3 多功能剪切试验仪Fig.3 Multifunctional shear tester

开展不同角度节理面的左侧-直剪试验和右侧-直剪试验。先安装试件，通过法向千斤顶逐渐施加预定法向力，再加上上部节理面试件的重力，所得到的总法向力除以节理面的面积，最终相当于对节理面施加18.72、29.78、40.85、51.92、74.05 kPa的法向应力。固定剪切试件上法向应力大小，并进行水平剪切试验，剪切人工节理试件的加载方式为步

进式，位移加载速率为每步0.05 mm。在剪切过程中，用千斤顶链接的表盘记录剪切力的大小，用百分表记录岩块下盘剪切位移值。

1.3 试验结果

多组试件进行直剪试验后，得到同一节理面左侧-右侧剪切试验的应力应变曲线如图4所示，以节理面Ⅰ为例，即θ=0°剪切方向为左侧剪切节理方向，θ=180°剪切方向为0°右侧剪切节理方向。由图4可知，不同方向下剪切节理面试件得到的抗剪强度不同，且同一方向下节理面试件进行左侧剪切和右侧剪切，其应力应变曲线亦不同。根据上述试验结果，可知同一节理面的各个方向对于岩石节理面剪切强度的影响不容忽视。剪切人工试件，得到不同节理面的应力应变曲线如图5所示，以60°方向的不同节理面为例，从图5看出不同节理面峰值抗剪强度差异较显著。

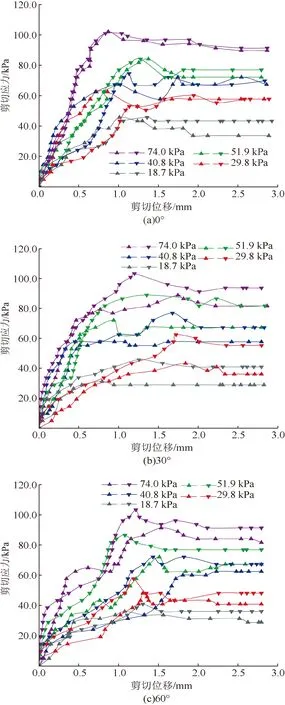
图4 同一节理面(Ⅰ)左侧剪切-右侧剪应力-剪切位移曲线Fig.4 Left shear stress-right shear stress-stear displacement curves of the same joint plane (Ⅰ)

图5 同一方向(60°)不同节理面的剪应力-剪切位移曲线Fig.5 Shear stress-shear displacement curves of different joints in the same direction(60°)

剪切试验结束后，将岩块取出，可根据节理面形态及剪切位移-剪切应力曲线将剪切破坏划分为3个阶段。

(1)压密阶段。当法向千斤顶逐渐对岩石节理面施加法向应力，而剪切应力未施加时，上、下节理面试样逐渐开始靠近，两者之间间隙被进一步压密。

(2)爬坡阶段。随着水平位移增大，上、下节理面之间出现错动，施加剪应力的试块开始沿着剪切方向向上滑动爬坡，节理面产生沿剪切方向爬升和摩擦效应，可以观测出背坡一侧相邻节理面之间已明显脱离，节理面上微凸体开始出现碎裂。

(3)破坏阶段。逐渐增大水平剪应力，遵循剪胀效应的作用，节理面之间实际接触面积逐步缩小，以致抵抗剪切破坏能力下降，当达到临界状态时，凸起体被剪断。剪切试件以及破坏节理面如图6、图7所示。节理试样的峰值抗剪强度实验值如图8所示。

图6 试件剪切破坏Fig.6 Shear failure of specimen

图7 试件剪切破坏节理面Fig.7 Shear failure plane of specimen

σn为作用于结构面上的正应力；τ为抗剪强度图8 各节理面的峰值抗剪强度Fig.8 Peak shear strength of each joint plane

2 节理面抗剪强度计算方法研究

2.1 三维粗糙度系数

Yuan等[11]提出的二维计算公式为

JRC=p1eCRRAWAG+p2CRRA+p3WAG

(1)

式(1)中：p1、p2和p3为经验系数，其值分别是-1.277、118.080和-52.965；CRRA为剖面线累积相对起伏幅度；WAG为加权平均梯度。

在x-z坐标系下，节理剖面线进行数字化分析，如图9所示，其计算公式如下。

图9 计算CRRA和WAG的示意图Fig.9 Schematic diagram for calculating CRRA and WAG

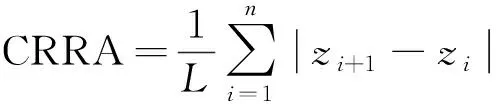
(2)

(3)

式中：zi+1-zi为节理面上下高度差；Ai为接触面积；L为岩石节理面剖面的总长度；n为考虑的采样间隔数。

基于以上二维JRC值计算公式提出节理面三维粗糙度参数JRC3D计算方法，步骤如下。

步骤1对节理面沿着剪切方向与剪切方向垂直的方向上，等间距选取轮廓线位置坐标，间距与CRRA和WAG的采样间隔数一样，即Δx=Δy=xi+1-xi。如图10所示，节理面x方向取121个点，y方向取121条轮廓线。

图10 节理面沿x、y方向取值Fig.10 Values of discontinuities along x and y directions

步骤2由式(2)和式(3)分别计算每条节理面二维轮廓线的CRRA、WAG和JRC。

步骤3对节理面的每个轮廓线的JRC进行加权平均得到节理面三维粗糙度参数JRC3D，见表2。

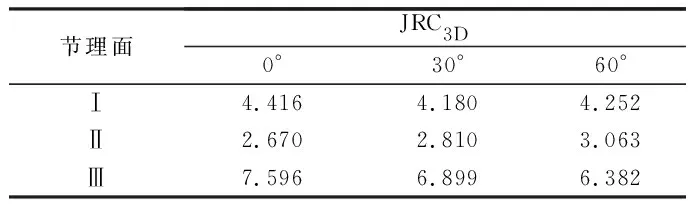
表2 节理面三维参数 Table 2 Three-dimensional parameters of surface

通过试验结果分析，同一节理面沿剪切方向的三维粗糙度系数JRC3D是一定的，但不同方向剪切的峰值抗剪强度却不相同，观测图6和图7中各人工节理试件的剪切结果，将节理面试件按不同方向剪切简化的过程如图11所示。

根据图7和图11可以明显看出，剪切方向一定时，节理面剖面之间的接触面积是一定的，即初始节理面的实际接触面积是不变的；因剪切方向的改变，会使同一节理面剖面的实际接触面积会发生改变，从而影响峰值抗剪强度的变化。

图11 同一节理面不同剪切方向示意图Fig.11 Schematic diagram of different shear directions on the same joint plane

由上图9可得出，其坐标轴沿剪切方向变化的节理面剖面线图。当zi+1-zi<0时，可以计算得出节理面剖面的倾斜曲面总长；根据三维扫描的节理面数据，通过软件分析计算得出粗糙节理面的面积As与节理面水平剪切平面面积Aj。其计算式如下。

推荐理由:好的记忆力无论对学生的学业还是成人的进修都有非常大的帮助作用，本书以目前最先进的记忆方法“记忆宫殿”为主题，讲解了人们如何快速轻松地掌握记忆法，并在学习生活和工作中灵活运用记忆法，提高自己的效率，注重科学性、实用性和高效性，不到一年6万册的销量也证明了本书真正满足了读者自我提升的需求。

当zi+1-zi<0时，求得每条轮廓线的实际接触曲面长，公式为

zi+1-zi<0

(4)

对于y方向的实际接触曲面长与其轮廓线总长度的比值，并进行求和平均得

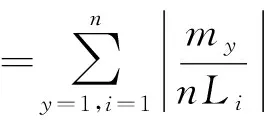
(5)

求出面向剪切方向接触面积值M为

M=Asm

(6)

然而几何分析的接触面积值并不能完全提供节理面试件的抗剪强度，因此通过计算节理面面向剪切方向面积值与净粗糙面面积(As-Aj)的比值来定义粗糙节理面的接触面积有效系数值a，公式为

(7)

式(7)中：As为粗糙节理面的面积值，节理面Ⅰ为44 482 mm2，节理面Ⅱ为44 266 mm2，节理面Ⅲ为44 695 mm2；Aj为剪切平面面积值，为43 637 mm2。

节理试件各个剪切方向下系数a如表3所示。定量分析各个方向a的大小。可以得出，相同节理面进行不同方向剪切时，a不相同，抗剪强度值亦不同；人工节理试件表面越粗糙，a也会越小,则进行直剪试验时实际接触面所提供有效接触面积也就越小。系数a的提出，可以定量描述沿不同方向剪切节理面时，抗剪强度差异的原因。

表3 节理面沿剪切沿方向接触面积有效系数值Table 3 Effective coefficient values of joint surface contact area along shear direction

2.2 图拟合剪胀角公式

τ=σntan(ip+φb)

(8)

式(8)中：φb为结构面内摩擦角；ip为剪胀角。

研究节理面的剪胀角变化情况，依据人工节理试件沿左、右方向进行剪切，得出剪胀角的试验值。图12是描述多种粗糙节理面各个剪切方向下剪胀角与法向应力变化情况。根据试验结果可知：同一节理面，不同方向进行直剪试验得出的剪胀角不同；节理面同时进行左侧、右侧剪切试验得出的剪胀角亦不相同；同一节理面，剪胀角随法向应力的增大而减小；法向应力相同时，节理面越粗糙，剪胀角越大。

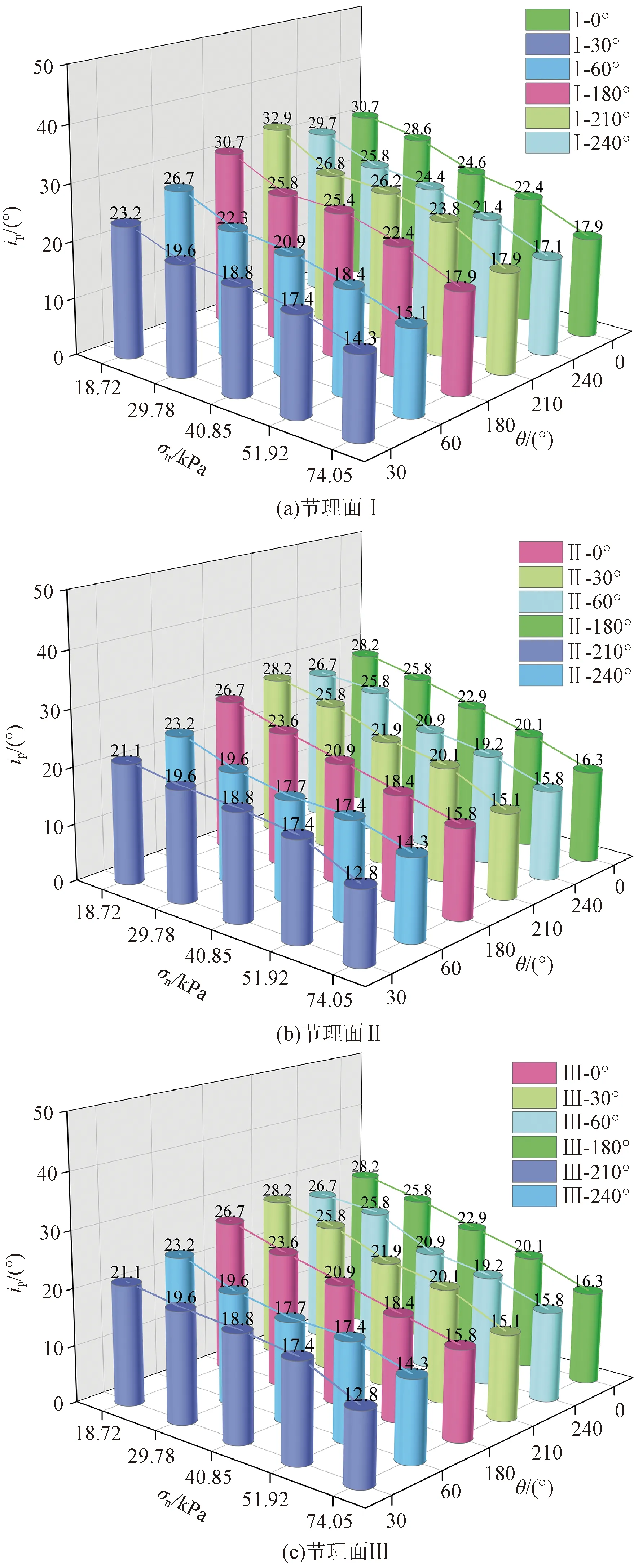
图12 不同节理面剪切方向下剪胀角与法向应力图Fig.12 Dilatancy angle and normal strain diagram of joint plane under different shear directions

根据剪切试验中剪胀角与法向应力的关系，以及剪胀角受抗拉强度、抗压强度等的影响，利用非线性拟合方法建立ip的函数。剪切试验中不同节理面剪胀角与法向应力之间的拟合关系如图13所示。函数表达式为

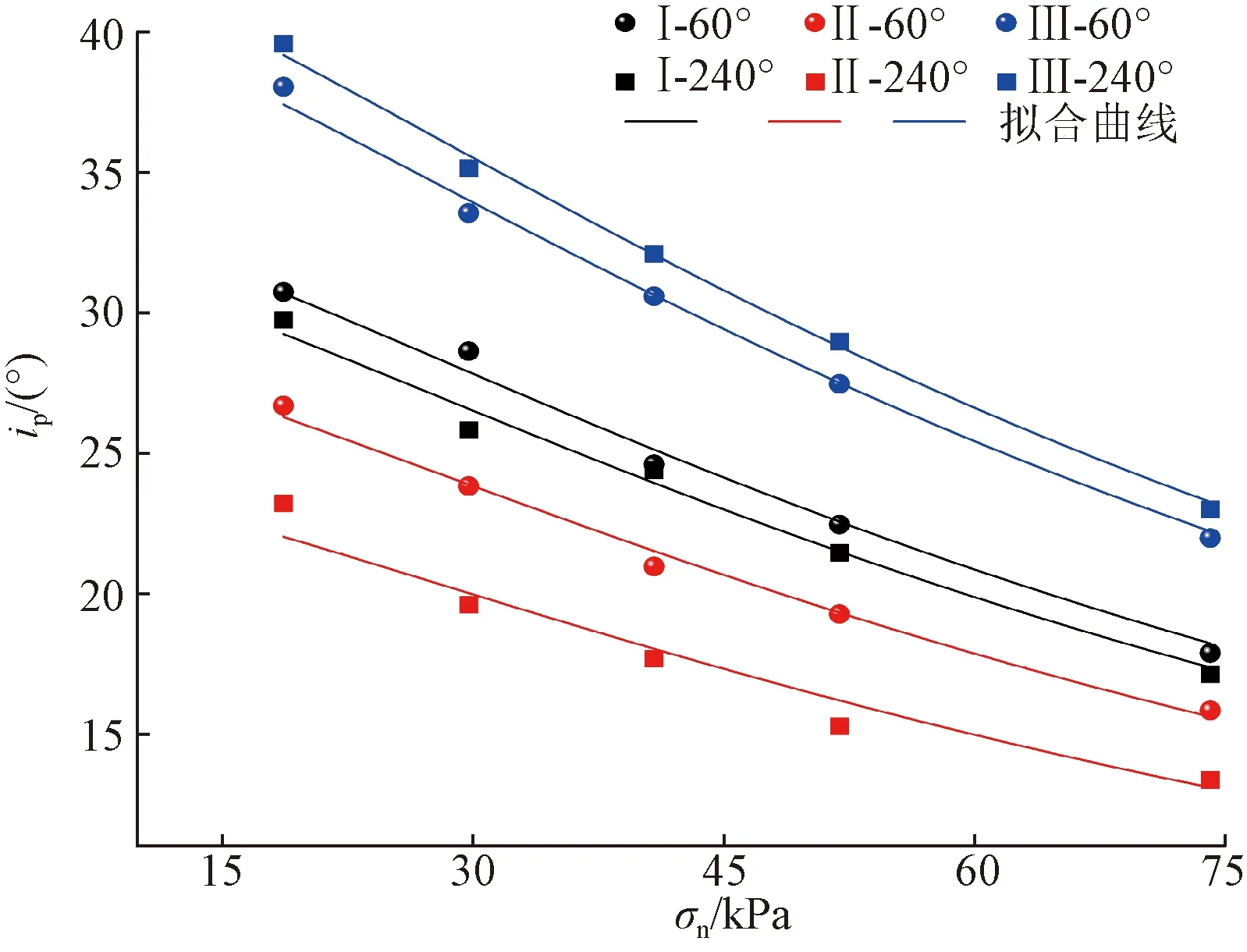
图13 节理面剪胀角与法向应力之间的关系Fig.13 Relationship between dilatancy angle of joint surface and normal stress

(9)

式(9)中：c、d和h均为拟合系数，其值分别为145.49、1.5和3。

2.3 数值计算抗剪强度公式

将式(9)代入式(8)中，可得出基于不同剪切方向下含有三维形貌参数的抗剪强度模型为

(10)

提出的岩石抗剪强度新模型，利用三维粗糙度系数来描述节理岩体的形貌特征；同时又引入沿剪切方向接触面积有效系数值a，用以描述沿各个方向剪切的差异性；而且该模型体现了剪切破坏时抗压强度、抗拉强度和粗糙度系数等在不同法向应力下对剪切强度的影响；系数a的提出，描述节理面剪切破坏更具有直观性，物理意义明确。

3 公式的验证与比较

3.1 三维粗糙度系数分析

对于目前的岩石研究领域，Barton等基于大量实验提出的JRC-JCS峰值抗剪强度准则是适应性最为广泛的经验模型。其表达式为

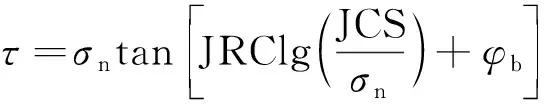
(11)

式(11)中：τ为岩石节理峰值抗剪强度；σn为有效正应力；JRC为节理粗糙度系数；JCS为节理面壁面强度；φb为基本摩擦角。

根据Barton模型提出的10条典型粗糙度节理面剖面线，并人为估算JRC的值，具有典型的二维性，难以准确计算出真实节理面的粗糙度系数。这里对于JRC的计算采用Yang等[23]使用轮廓线一阶导数均方根Z2，利用几何统计函数来建立节理面JRC与Z2的关系。

(12)

JRC=32.69+32.98lgZ2

(13)

式中：y为节理的轮廓线高度；Δx为采样区间；yi+1-yi为相邻两个采样点的高度差；m为区间的个数。

JCS取未风化新鲜节理单轴抗压强度。计算出Barton公式各人工节理参数值见表4。

表4 Barton模型节理面参数Table 4 Joint surface parameters of Barton model

3.2 抗剪强度分析

图14为Barton模型[式(11)]和本文模型[式(10)]得到的抗剪强度计算值与实验值的比较。由图14可知，Barton模型计算强度值与实验值相比存在较大偏差，本文模型的计算值与试验值具有很好相关性。

图14 本文模型与Barton模型比较Fig.14 Comparison between this model and Barton model

分析原因，Barton模型中节理面粗糙度参数JRC本身具有二维性质，难以满足真实节理面三维粗糙度要求。JRC3D计算是利用几何形态函数统计的方法，避免了人为经验观测的误差。剪胀角应具有描述岩石节理面三维形貌特征的性质，与其节理面的各项力学参数有着至关重要的联系，难以用Barton公式中的JRC-JCS这两个力学属性去描述。因此Barton模型计算结果与实验值之间偏差较大。

对于模型的抗剪强度准测值与试验值，可以分析它们的平均相对误差，来比较模型与试验值的一致性。其计算式为

(14)

式(14)中：σave为平均相对误差；n为节理试件取样个数；τpt为抗剪强度试验值；τpc为模型计算值。

对于模型的平均计算偏差结果见表5。

表5 节理岩体模型平均偏差Table 5 Average deviation of jointed rock mass model

4 结论

通过逆向制作人工岩石节理试件，并进行常法向应力下的直剪试验，从摩尔-库伦强度准则出发对剪胀角与法向应力进行分析，从而建立不同剪切方向下的抗剪强度新模型，并与经典Barton模型进行对比，得出以下结论。

(1)Barton模型是一个经典的二维经验公式，对于传统粗糙度系数JRC的评定，存在人为主观因素。其模型粗糙度系数相较于本文模型采用几何统计函数来精确计算节理面三维粗糙度系数JRC3D明显有较高的偏差。说明二维计算节理面参数的方法无法准确描述岩石节理面的抗剪强度，且单一力学参数并不能完全表征节理岩体的抗剪力。

(2)通过对室内直剪试验结果进行分析，对于节理面的各个方向差异性提出沿剪切方向接触面积有效系数a。可以看出，人工试件的节理面越粗糙，则系数a会越小；同一节理面沿不同方向剪切时，节理岩体所提供的接触面积有效系数值各不相同。系数a能够体现岩石节理剪切时各个方向的差异性，也是分析抗剪强度不同的重要原因。

(3)通过量化三维节理面的方法，用几何统计函数来表征节理面粗糙度系数，可以反映剪切作用下岩石节理面的爬升与摩擦效应。本文模型中剪胀角的计算公式，符合剪胀角随法向应力和节理面粗糙度的变化规律，可以得出该模型计算不同剪切方向下岩石节理面的抗剪强度具有较好的可靠性。