基于排队网络模型的航站楼资源优化配置研究

2022-02-03华文静杜皓月

无线互联科技 2022年22期

华文静，杜皓月，王健

(1.南京市交通运输综合行政执法监督局，江苏南京 211106；2.南京航空航天大学民航学院，江苏南京 211106；3.华设设计集团股份有限公司，江苏南京 210014)

0 引言

我国民航机场航站楼建设经历了从新中国成立初期规模小、功能简单，改革开放时期规模与空间品质明显提升，到现阶段超大体量且更注重智能化和生态化的过程。航站楼的设计最初依靠对国外航站楼的模仿借鉴。现阶段，大多采用手册法进行相关指标的计算，即以国际民航组织文件及局方发布的标准规范作为航站楼建设的理论依据。手册法简单方便，但考虑的旅客服务指标单一，实际使用中往往存在设施不足、旅客出行体验不佳，或设施过量、利用率低下等问题。因此，如何在手册法基础上优化资源配置显得尤为重要。

在手册法的应用上，Ashford等回顾了国际航空运输协会(International Air Transport Association，IATA)、英国机场管理公司(British Airports Authority，BAA)、欧洲各机场等对航站楼设施服务水平的评估标准，以此作为设定各项设施服务水平上、下限的参考。国内也开展了中国民用机场服务质量评价工作，93家年旅客吞吐量超过100万人次的运输机场参评。马俊鹏[1]参照IATA提出的服务标准计算了航站楼的总面积与主要功能分区的面积。

排队论法是指应用经典排队模型来评估服务设施效率。国内学者对航站楼功能分区的研究相对较少，主要采用排队论的方法对单个环节进行分析，而将航站楼流程作为一个整体的网络系统的研究则不够深入。阳旭[2]通过换乘矩阵的分析，从距离、导向、空间、文化4个方面提出航站楼内部空间设计的建议策略。张天炫等[3]基于社会力模型提出了旅客出港排队流程分析仿真模型。高宁煜等[4]建立开放式网络排队模型，分析了不正常航班现象发生后各节点的旅客人数变化，并对其加以控制。刘英[5]、邢志伟[6]、张天炫[7]等针对值机环节构建了基于M/M/1的多种旅客排队系统模型，用于值机柜台的优化配置。赵元棣[8]、胡艳敏[9]等分析了安检流程的限制因素，找到该流程的瓶颈环节，据此对安检布局进行调整。

国外学者对机场航站楼的研究较早，从20世纪50年代起已有相关研究，主要集中在服务柜台指派、流程仿真模拟等方面，但对航站楼的整体流程环节研究也相对较少。Li等[10]比较了安检柜台前的不同排队方式，研究发现，在安检设施相同的情况下，为有行李旅客分配更多的资源可以提高安检效率。Parlar等[11]根据新加坡樟宜机场的经验数据，研究了为单个航班分配的值机柜台开放数量的动态优化问题。Liu等[12]调查了3个季节的典型月里中国枢纽机场航站楼不同区域的客流情况，重点研究了停留时间和旅客数等主要指标。Ruiz等[13]提出了一种能够详细模拟安检过程的离散事件仿真模型，并以凤凰城天港国际机场为例进行实验分析，提出采用仿真的方式识别安检中的热点，从而有针对性地改善旅客等待时间过长的问题。

本文以航站楼的资源优化配置为研究对象，提出了排队网络模型用以解决航站楼设计中服务设施资源计算的问题，并以江苏某机场为例验证了该模型的有效性及合理性。

1 航站楼排队网络

1.1 网络构建

关于航站楼的旅客流程，多数研究都是针对单个环节进行，单独分析值机、安检等环节的排队方式、柜台分配等问题。然而，实际运行中的各流程并非相互割裂、独立进行，而是作为一个密切联系的网络系统相互影响。排队网络与排队系统的区别在于：在排队系统中，一个顾客只在一个服务台接受服务；在排队网络中，多个排队系统互相连接，其中任何一个排队系统里完成服务的顾客可选择离开，或加入其他排队系统继续接受服务。

航站楼的旅客流程可视作排队网络。值机时，若采用专用值机方式，各柜台只能办理特定航班旅客的值机手续，旅客排队方式一般为单柜台单队列形式，多个队列构成并行的排队系统；若采用公用值机方式，各柜台可办理所有航班旅客的值机手续，则有单柜台单队列和多柜台单队列两种形式，对于后者，公用柜台构成一个排队系统。在安检排队系统中，值机、安检、联检3个环节之间相互串联，各环节内部可能还存在并联，整个旅客流程构成排队网络。

1.2 网络分析

排队网络可分为3种基本类型：开环网络(至少有一个与外界连接的输入流和输出流)、闭环网络(无外部输入和输出)、混合网络(所研究的排队网络对某类顾客是开放的，而对其他类顾客是关闭的)。根据以上定义，旅客流程构成的排队网络属于开环网络，又叫Jackson网络，具有M个节点的排队网络(标记为i=1,2,…,M)满足以下条件：每个节点i的服务时间相互独立且服从负指数分布；从系统外到达系统中任何节点i的外部输入是泊松到达过程且到达率λi≥0；一个顾客在某节点接受完服务后，选择离开网络或者进入另一个节点接受服务的概率与过去历史无关。在航站楼排队网络中，旅客到达率将前后各环节的排队系统衔接起来。假设整个排队网络有m个阶段，各阶段有s个并行的子排队系统，则：

λ1(t)=λ2(t+T12)=…=λm(t+T1m)

(1)

λi(t)=η(i-1),1(t)+η(i-1),2(t)+…+η(i-1),s(t)(2)

式(1)反映了串联排队系统旅客到达率的关系，其中λi表示i环节的旅客到达率，Tij表示第j环节的排队系统相对于第i环节的滞后时间。式(2)反映了并联排队系统旅客到达率的关系，η(i-1),j表示从第(i-1)环节的第j子系统转移到第i排队系统中的到达率。

2 相邻环节的衔接性优化

2.1 等服务速率法

考虑值机和安检环节的系统性和连续性，采用等服务速率法将两系统的服务台设置数量按照一定比例进行控制，使两个环节的服务能力相匹配，得到较为平稳的排队过程。

(3)

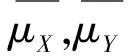
(4)

其中NX，NY分别表示值机和安检系统的到达总人数，由此可得两系统的服务台开放数量之比：

(5)

2.2 图解法

式(5)提供了相邻两环节顺畅衔接时的服务台设置数量的比例关系，若需获取其开放数量具体数值，还应利用排队论公式进一步计算。当航站楼某排队系统处于稳态时，旅客到达时间间隔、服务时间均服从泊松分布，设服务台数为k，则该排队系统为M/M/k。若旅客到达率为λ人/分钟，每个服务台的服务率为μ人/分钟，服务强度ρ=λ/μ。根据排队论[14]，有以下表达式：

(6)

(7)

(8)

(9)

以上各式中Lq为旅客排队长度，Wq为旅客排队等待时间，Ws为旅客系统逗留时间，W为机场期待实现的某等级服务水平下系统内停留时间标准。令Ws=W，则可通过以上各式解出该系统所需服务台数k。由于计算k时，需求解非线性方程，故采用图解法：绘制队长Lq与柜台数k的曲线图，查找该曲线与水平直线LC的交点，即可确定k的值，其中LC为在期望服务水平下的旅客排队长度。

3 累积图法分析

在机场航站楼实际运行中，各排队系统不一定处于稳态，旅客到达率随时间变化，各服务台开放数量也受到时间、政策等因素影响。因此，航站楼旅客排队系统是一种非稳态的串并联混合式开放网络。对于此种排队网络，难以用公式直接求解其运行效率指标，故采用累积图法，即绘制系统中单位时间旅客数、累计到达及服务旅客数随时间变化的曲线图，研究旅客到达率不变而服务率变化，以及服务率不变而旅客到达率变化两种情形。

3.1 旅客到达率变化的服务模型

航班时刻表中飞机起飞时间的不均匀性，导致旅客到达机场的时间分散。随着旅客到达人数从波谷进入波峰，高峰时期机场航站楼内服务设施全部投入运营，保障能力接近饱和。旅客流波峰结束后，航站楼内设施仍需为积压的旅客提供服务。在这一过程中，航站楼设施的服务率几乎保持不变，而旅客到达率经历了增长随后降低的变化。将以上情形抽象化，得到理想情况下的旅客到达率变化的服务模型。

图1(a)中，S表示服务率，Al和Ah分别表示波谷和波峰时期的旅客到达率。a时刻前，旅客到达率小于服务率，无旅客排队；a～b时间段内，旅客到达率大于服务率，旅客累积量以(Ah-S)的速率增长；b时刻后，旅客到达率恢复，被延误的旅客量以(S-Al)的速率减少；c时刻时，延误现象消失。以横轴为x轴，纵轴为y轴，可得排队旅客量即折线adc的表达式为：

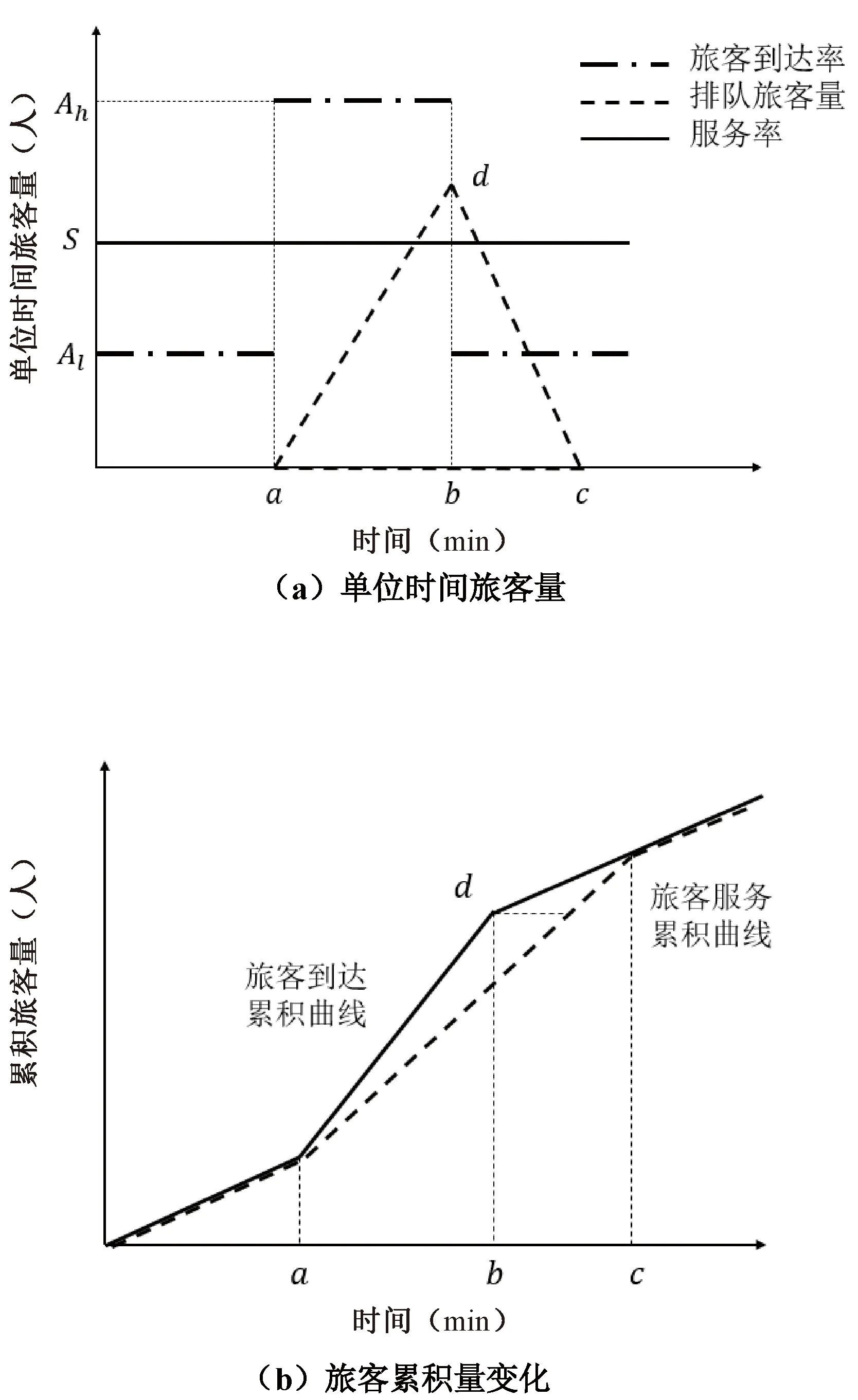
图1 旅客到达率变化的服务模型

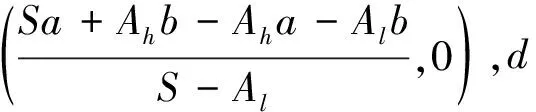
需排队的旅客总时数：

需排队的旅客总数：

Nq=Ah(b-a)+Al(Tq-(b-a))

平均每位旅客排队时间：

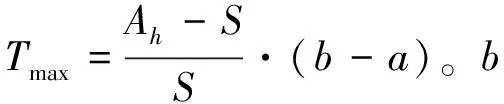
3.2 旅客服务率变化的服务模型

航站楼实际运行中还可能出现旅客服务率变化的情形，即一段时间内旅客到达率不变，而现有服务设施速率不足以满足旅客到达需求，故需提高服务率以消除旅客排队现象。图2(a)中，A表示旅客到达率，Sl、Sh分别表示不同服务水平下的旅客服务率。假设d时刻之前不存在旅客排队，d～e时间段内，旅客到达率大于服务率，旅客累积量以(A-Sl)的速率增长；e时刻之后，服务率有所提升，队列长度以(Sh-A)的速率减少，直至f时刻队列消失。

以横轴为x轴，纵轴为y轴，可得排队旅客量即折线dgf的表达式为：

(11)

与旅客到达率变化的服务模型类似，可计算得到：

平均每位旅客排队时间：

队列长度(纵坐标之差)：

排队时间(横坐标之差)：

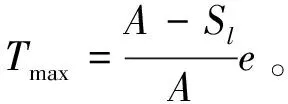
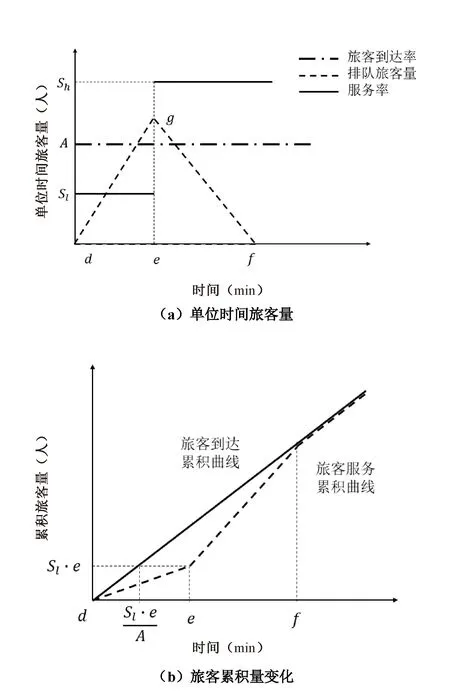
图2 旅客服务率变化的服务模型

4 实例分析

以江苏某机场航站楼内值机和安检两环节为例，应用排队网络模型对服务资源的优化配置进行实例分析，并与手册法进行对比。

2019年全国民航工作会议指出，千万级机场自助值机旅客占比力争达到70%以上。据现场调查统计，深圳宝安机场人工值机柜台服务速率低速时为1.1人/分钟，高速时可达1.3人/分钟；自助值机柜台平均服务速率约为1.4人/分钟；普通安检通道服务速率约为2.3人/分钟，VIP安检通道服务速率约为2.48人/分钟。参考现有机场设备的服务能力及未来科技发展趋势，将江苏某机场服务速率定为：人工值机柜台1.4人/分钟，自助值机柜台1.5人/分钟，安检通道2.5人/分钟。

4.1 手册法

手册法是指参考国际民航组织及民航局发布的文件中相关服务标准计算服务设施数量，即以高峰小时旅客数与高峰小时服务速度相除，得到设施数量。江苏某机场年吞吐量1 200万人次，高峰小时旅客吞吐量4 200人次，相关旅客流量数据见表1，值机及安检两环节的相关服务时间标准见表2[15]。按照人工值机与自助值机旅客数3∶7的比例，可得国内人工值机柜台数8个，自助值机柜台数17个，安检通道数14个。

表1 旅客流量数据(单位：人)

表2 值机/安检环节旅客服务时间标准(单位：min)

4.2 排队网络模型

4.2.1 等服务速率法

在对江苏某机场航站楼进行规划设计时，主要考虑满足其高峰时刻的旅客需求。由于安检环节在值机之后进行，旅客的到达具有一定的滞后性，IATA认为这一滞后时间平均约等于10分钟，故安检环节旅客到达率为1 733人/小时。按3∶7的比例对人工、自助值机柜台服务速率加权平均，得到值机环节综合服务速率为1.47人/分钟。由式(3)—(5)，高峰时刻每开放一条安检通道，可与2.04个值机柜台的服务能力相匹配。

4.2.2 图解法

相较于值机环节，旅客在安检环节的等待时间更长，拥堵更严重，因此选择依据值机柜台设置的数量来对安检通道进行优化。国内旅客到达率为34.65人/分钟。其中，人工值机旅客到达率为10.395人/分钟，自助值机旅客到达率为24.255人/分钟。分别绘制人工及自助旅客排队长度与服务台数的关系，如图3所示。达到机场设计标准时应至少设置人工值机柜台9个，自助值机柜台17个。为了使值机、安检环节平稳衔接，采用等服务速率法求得两环节的柜台数量存在2.04∶1的关系，故安检通道宜设置13个。

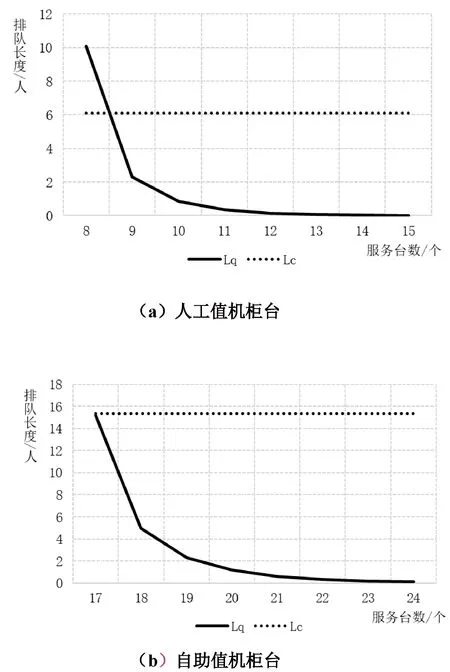
图3 服务台数量

4.2.3 累积图法

在非稳态的串并联混合式开放网络条件下，模拟航站楼的实际运行情况，根据前两小节按手册法及排队网络模型得到的服务台开放数量绘制累计图，对比分析相关排队指标，以验证本文提出的排队网络模型的有效性及合理性。

(1)情形设定。

现参照其他机场实际运行情况及服务设施的保障能力，对江苏某机场值机及安检环节的相关参数模拟值进行以下规定(见表 3)。在研究时间范围0500～1000时间段内，假设0600～0800时间段为离港高峰期。高峰小时值机服务率1.5人/分钟，安检服务率2.5人/分钟，国内旅客到达率1 700人/小时；非高峰小时值机服务率1.3人/分钟，安检服务率2.3人/分钟，国内旅客到达率1 400人/小时。前文已求解得到，按手册法应设置值机柜台25个，安检通道14个；按排队论模型应设置国内值机柜台26个，安检通道13个。高峰时期服务设施全部投入使用，非高峰时期值机和安检柜台开放数量按2.04∶1的比例相应减少。相比于前序值机环节，安检环节的旅客到达具有一定的滞后性，两者以串联形式产生关联。若值机旅客到达率大于服务率，即现有设施不能为所有旅客提供服务，限制了部分旅客向下流动，则安检旅客到达率为值机服务率；反之，所有旅客均可继续向后推进，安检旅客到达率为值机旅客到达率。

表3 江苏某机场值机区及安检区有关数据

(2)结果比对。

在设定情形下，值机环节的服务水平优于安检环节，依据手册法及排队网络模型所求，服务台数量配置均无排队，如图4所示。在安检环节中，排队网络模型会产生排队现象。0500-0800时间段内旅客到达率及服务率均有变化，可将前两小节的服务模型综合起来进行分析。

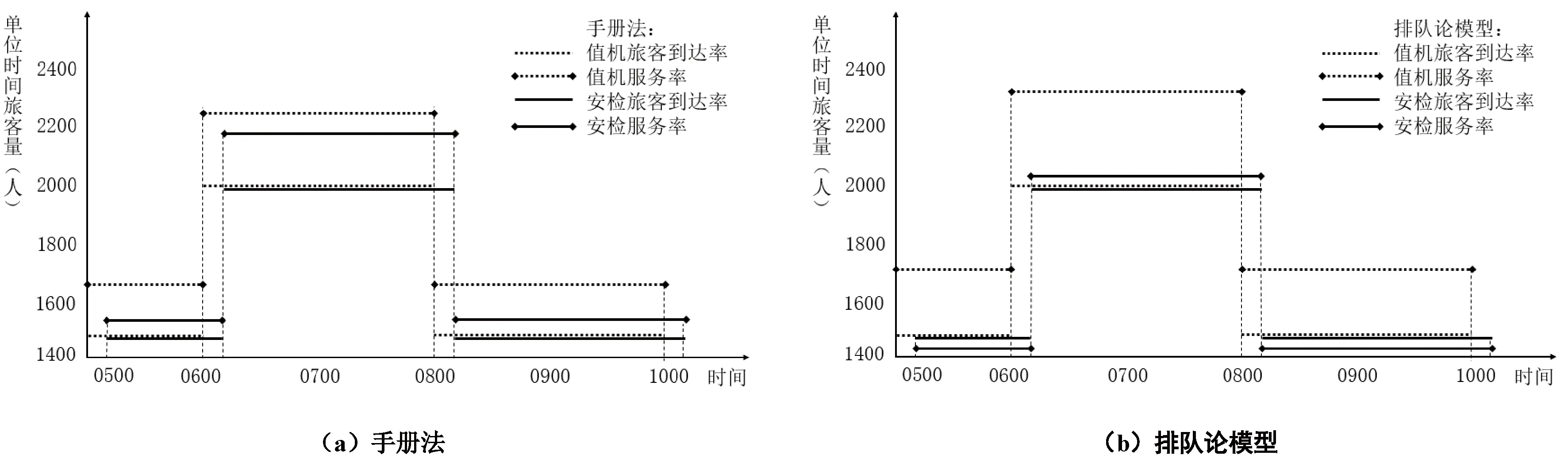
图4 单位时间旅客量

以开放值机柜台的时间0500为时刻0，图5描述了由非高峰时期进入高峰时期的累积旅客量变化。假设机场从0500开放值机柜台，此时旅客开始陆续到达，由于值机服务率大于旅客到达率，该环节无旅客排队。在安检环节，排队现象从0510持续到0736，共156分钟。其中，0608时到达的旅客排队时间最长(1分钟)，0610时排队队列最长(40人)。总时数48.6人·分钟，总排队人数80.04人，故平均每位旅客排队时间0.61分钟。

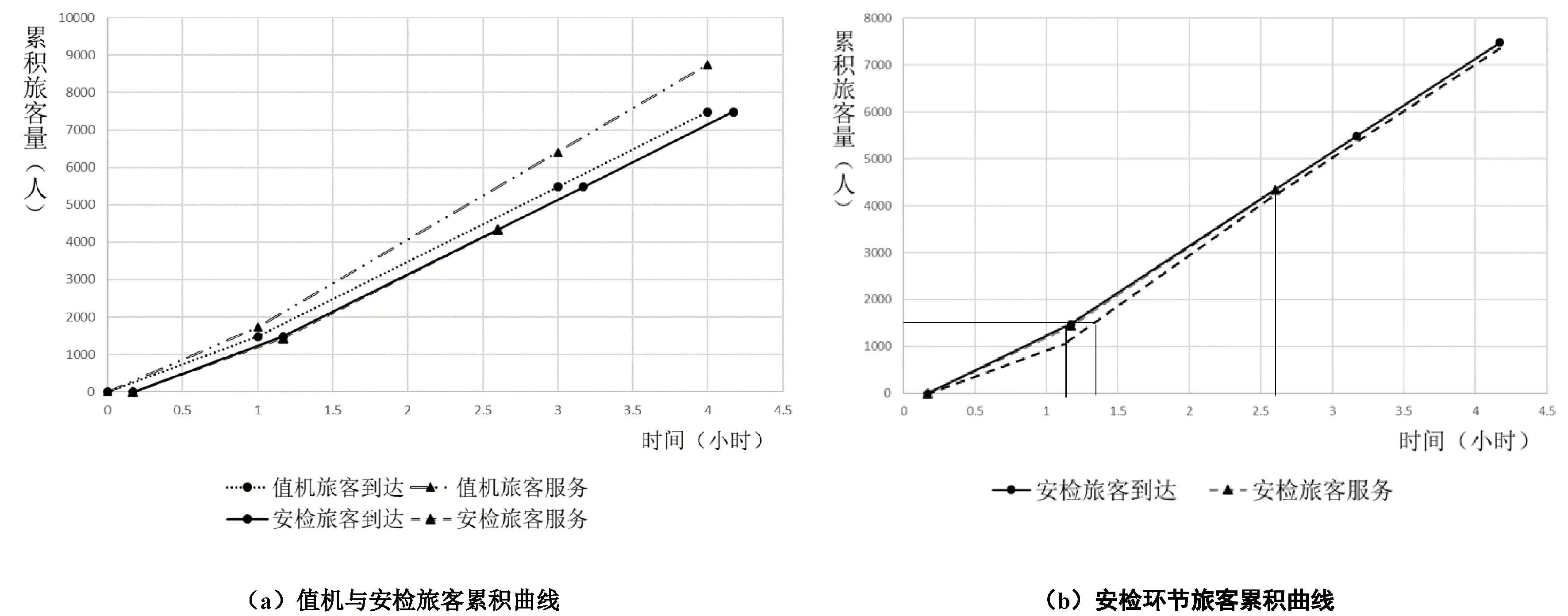
图5 旅客累积曲线

由表 2可知，值机环节国内航班经济舱旅客等待及办理时间不应超过10分钟，安检环节经济舱旅客也不应超过10分钟。在值机服务时间1.5分钟、安检服务时间2.5分钟的情况下，依据排队网络模型求得旅客安检时最长排队时间1分钟，平均排队0.61分钟，无值机排队现象。以上旅客排队指标均在可接受范围内，对航站楼的正常高效运行影响较小。而按手册法求解的安检通道数量过剩，造成了服务资源的浪费。故在江苏某机场航站楼设计中，应设置国内值机柜台26个，相应的安检通道13个。