SMA驱动变体机翼后缘结构连续偏转模糊控制方法研究

吴 梦，徐志伟

(南京航空航天大学 航空学院，江苏 南京 210016)

0 引言

变体飞行器是指在飞行过程中可主动地改变飞行器主要结构(机翼、机身、进气道等)的相关参数，以适应不同飞行条件并能够获得最优飞行性能的飞行器。在变体飞机中，变体机翼是最重要的研究方向，主要包括：可变后掠角机翼、前后缘襟副翼偏转机翼、可变厚度机翼等各种类型。其中，机翼后缘襟副翼光滑连续偏转是重要的研究方向之一，国内外的很多学者和研究机构对此进行了广泛的研究[1-4]。

在机翼变体过程中，常规的驱动方式如液压、电机等成熟可靠，但体积和重量较大，无法满足机翼的设计要求，采用智能材料驱动器和多点分布式驱动是一种新型的解决方法[5]。在多种智能材料驱动器中，形状记忆合金SMA(Shape Memory Alloy)因具有高功重比、尺寸小、可消除复杂传动系统等优点，成为机翼变体结构中的首选驱动器之一。镍钛合金材料经过一定的工艺处理后，具备形状记忆功能，即在低温环境中受外力作用发生变形后，对其加热至一定温度可恢复至初始形状，因此被称为形状记忆合金。SMA材料内部主要存在两种合金相，低于所设定的温度时为马氏体相，此时SMA的弹性模量较小，容易产生变形；高于设定温度时为奥氏体相，此时SMA的弹性模量较大，变形过程中可产生很大的回复力，可以作为驱动器使用。但是，SMA材料易受外部温度和外力的影响，具有很强的时变性，而且SMA本身具有很强的迟滞性和非线性，因此难以建立精确的数学模型，实现对其变形和驱动力的精确控制。针对这一问题，国内外学者开展了大量研究，Bizdoacan等[6]针对一种基于SMA驱动的触手机器人结构及其数学模型，设计了滑膜模糊控制器并进行了仿真，仿真结果表明模糊控制器可提高系统的精度和响应速度。Kumagai等[7]通过线性函数的组合对SMA驱动器的迟滞曲线进行了简化，采用神经模糊方法建立了SMA驱动器的位移-加热电压动态模型并进行了跟踪实验，实验结果表明该模型在期望轨迹跟踪方面具有优势。Khodayari[8]设计了一种基于SMA丝驱动的三连杆蛇形机器人，该机器人结构中具有两个偏转极限为5°的转动关节，建立驱动器的数学模型后采用模糊PID控制方法对其进行了控制仿真，结果表明系统响应时间约20 s，稳态误差约0.2°。国内学者对SMA控制方法的研究起步较晚。任秉银等[9]设计了一种模糊PID控制系统，并对偏动式SMA驱动器的响应特性进行了仿真，结果表明该控制器可提高系统的响应速度。史振云等[10]研制了一种基于SMA驱动的转动关节，该关节的运动范围约±60°，建立了SMA丝的应变-电阻模型，基于该模型设计了模糊PID控制器并进行了阶跃响应实验，实验结果表明，旋转角度的平均误差约3.147°。

到目前为止，国内外学者对SMA驱动器的控制方法进行了深入的研究，其中模糊控制方法具有较好的控制效果，但都以相应的数学模型为基础，SMA材料的制备工艺和成分变化后，已有的模型很难适用于新型的SMA驱动器。针对这一问题，本文设计并制作了机翼后缘连续变弯度结构，采用差动式SMA丝作为驱动器满足后缘结构的双向偏转，研究并采用了模糊逻辑控制方法，实现对后缘偏转的精确控制。该方法无需建立SMA驱动器数学模型和系统的动力学方程，通过实验获取控制系统的相关参数，搭建了测控系统并进行了相关实验，获得了良好的控制效果。

1 SMA驱动可连续偏转机翼后缘变体结构

某机翼后缘要求能够实现±10°的上下偏转，机翼展长1.1 m、后缘弦长0.12 m，为实现机翼后缘的连续上下偏转，采用了多关节转动结构，如图1所示，后缘偏转过程中，为使翼面尽可能保持连续，采用分段翼肋和鱼鳞叠层蒙皮构型；为防止多段翼肋结构的干涉问题，采用3关节形式；其中关节1与机翼主骨架固定连接，相邻两关节铰接；加强梁将翼肋和后缘蒙皮连接，同时也是SMA丝驱动器的固定连接器件。后缘上下偏转采用了SMA丝差动驱动技术，每个转动关节中，将多根直径2 mm的SMA丝对称布置在机翼弦平面上下两侧。经实验测试其主要力学特性参数如表1所示，其中MS为马氏体相变开始温度，Mf为马氏体相变结束温度，AS为奥氏体相变开始温度，Af为奥氏体相变结束温度，DM为马氏体弹性模量，DA为奥氏体弹性模量，εl为最大残余应变。

图1 SMA驱动机翼后缘结构模型

表1 2 mmSMA丝力学性能

本文根据前期模型流场气动载荷仿真分析计算得到的气动载荷的要求，为确保SMA丝驱动器可产生足够的驱动力，在每个转动关节中上下共布置(2组)4根SMA丝。模型中根据实际后缘两个转动关节位移与载荷大小，每侧布置两组SMA丝，每组两根，每根长度为2 428 mm，计算得到最大偏转角度时最大变形量为2.04%。模型一侧SMA丝驱动器的布置如图2(a)所示。关节转动过程中，对一侧SMA丝加热，另一侧丝冷却，即可实现对应关节的小角度偏转，由于铰链结构的累积效应，即可实现整个后缘结构的大角度偏转。设定关节2和关节3的转动角度分别为α和β，后缘总体偏转角度为θ，则有如下关系。

(1)

在后缘结构中，以翼梢处的旋转关节为基准，设定按逆时针方向转动为正，关节2和关节3的转动范围分别设定为[-6°，6°]和[-6.8°，6.8°]，则后缘整体结构的偏转角度为±10°，模型中在两个转动关节处都配置有角度传感器，实现对关节偏转角度的精确测量，布置方式如图2(b)所示。每根SMA丝驱动器上都安装有热电偶温度传感器，实现对SMA丝驱动器温度的精确测量。

图2 机翼后缘结构中SMA驱动器及角度传感器布置

2 机翼后缘可变弯度模糊控制系统原理

SMA丝驱动器是通过控制温度实现驱动功能，本文中的SMA丝驱动器采用电流加热方式，利用脉宽调制(PWM)方法实现对SMA丝加热电流的控制，从而控制其温度；冷却过程则是采用自然冷却的方法。SMA丝驱动器的精确控制主要受两方面的因素影响，一方面，SMA丝性能的高度非线性和迟滞性，使得其温度控制非常困难；另一方面，在SMA丝工作过程中，易受当前环境温度、气流和外部载荷大小的影响，时变性使得难以建立精确的数学模型。

控制系统要求能够实现后缘结构±10°(精度±1°)的上下偏转，且在±10°位置在外部气动载荷作用下保持一定的时间。根据该要求并考虑到SMA丝驱动器的特点，本文采用了模糊控制方法，该方法针对控制对象没有准确的数学模型、强非线性、时变性和滞后性的特点具有一定的优势。所设计的模糊控制器原理如图3所示，先要确定输入和输出变量，输入变量的个数为模糊控制器的维数。一般而言，模糊控制器的维数越高，控制越精细，但维数过高会导致模糊控制规则复杂，控制算法难以实现。一方面为了防止模糊控制规则数目过多，使模糊控制器简单便于实现；另一方面，在SMA丝工作过程中，其温度-应力关系过于复杂，导致对SMA丝的温度进行模糊处理无法清楚地表达温度-应力关系。本文仅对各转动关节当前偏转角度误差及其变化率进行了模糊化处理，即设计了一种二维模糊控制器，其输入量为各转动关节当前偏转角度误差和误差变化率。图3中，r(t)为各转动关节期望偏转角度；c(t)为各转动关节当前偏转角度；e(t)为各转动关节当前偏转角度误差；ec(t)为各转动关节当前偏转角度误差的变化率；Ke和Kec分别为输入量e(t)和ec(t)的模糊化因子。将输入量e(t)和ec(t)分别与对应的模糊化因子相乘即可得到对应的模糊量e’(t)和ec’(t)；模糊推理决策根据e’(t)和ec’(t)在线推理出当前的控制量u(t)；u(t)经过解模糊得到PWM信号的占空比q(t)；q(t)经过控制逻辑处理后获得SMA丝加热信号(PWM)的实际占空比q’(t)，实现了脉宽调制对SMA丝加热电流的控制，从而控制其温度。e(t)的计算公式定义如下：

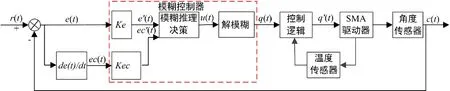
图3 模糊控制器原理

(2)

考虑到SMA丝的温度过高会影响其形状记忆功能，为了防止SMA丝温度过高和实现SMA驱动器的差动控制，本文所设计的控制逻辑如图4所示。以翼梢处的转动关节为基准，设定按逆时针旋转方向为正，则T1，T2分别为上、下侧SMA丝的温度；D1，D2分别为上、下SMA丝加热控制信号(PWM)的占空比。根据公式2，当e(t)为负时，此时系统已产生超调，考虑SMA丝的特点，此时应停止加热；当e(t)为正时，系统根据r(t)的符号判断应加热丝的方向和位置，比如当r(t)为正时，系统加热上侧SMA丝并冷却下侧SMA丝；当r(t)为负时，加热下侧SMA丝并冷却上侧SMA丝，从而实现SMA丝驱动器的差动控制。综合考虑SMA丝的相变温度、冷却速度和形状记忆性能保护等要求，经过多次试验，设定处于冷却状态中的SMA丝温度小于35℃时，方可对另一侧的SMA丝加热，处于加热状态中的SMA丝温度最高不能超过60℃。

图4 模糊控制器控制逻辑

2.1 控制系统输入变量的模糊化处理

模糊化是将精确量转换为模糊量的过程，精确量的取值范围为基本论域，模糊量的取值范围为论域。因此，模糊化的过程本质上是建立基本论域到论域映射关系的过程。本文根据各转动关节的转动范围和公式(2)，确定控制器输入量e(t)的基本论域；根据单位时间内偏转角度的误差变化不超过±6°的要求，确定ec(t)的基本论域；u(t)解模糊后为占空比q(t)，q(t)的取值范围即为基本论域。为确保模糊集能较好地覆盖论域，根据论域的最大值与最小值之差不小于对应变量模糊子集个数的两倍的设计要求，经多次实验，最终确定输入量e(t)、ec(t)和输出量q(t)的论域，各关节模糊控制器的相关参数如表2所示。分别通过公式(3)和公式(4)完成输入量e(t)和ec(t)的模糊化。

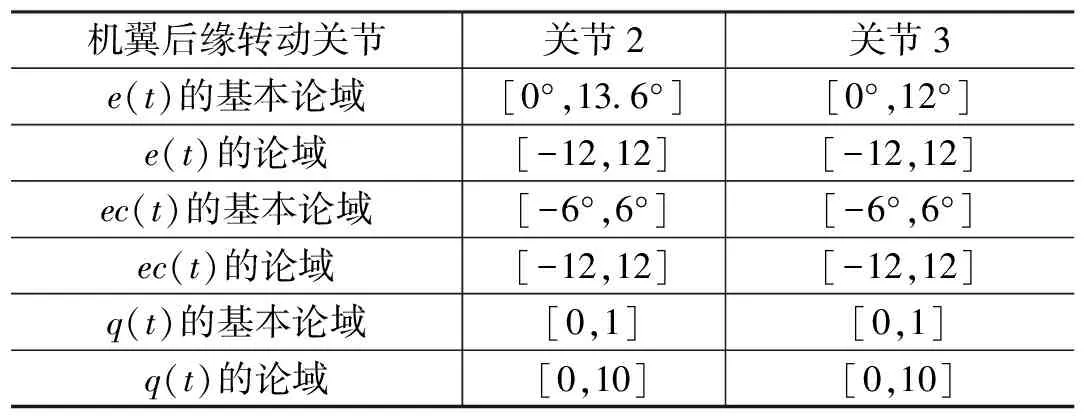
表2 模糊控制器的相关参数

(3)

(4)

式中：ae，be为e(t)的论域的最小值与最大值；ce，de为e(t)的基本论域的最小值与最大值;aec，bec为ec(t)的论域的最小值与最大值；cec，dec为ec(t)的基本论域的最小值与最大值。

2.2 输入、输出变量的模糊子集

定义模糊子集，实际上就是确定隶属函数曲线的形状，形状较尖的模糊子集具有较高的分辨率和灵敏度，如三角形隶属函数。定义模糊子集时需遵守3个基本规则：(1)论域中，任意一点的隶属函数最大值要大于0.4，否则会降低模糊控制器的控制精度。(2)模糊子集交叉点处的隶属函数值γ要在0.4～0.7范围内，γ较小时控制灵敏度较高，γ较大时模糊控制器具有较好的鲁棒性。(3)为确保模糊集能较好地覆盖论域，论域的最大值与最小值之差不小于对应变量模糊子集个数的两倍。为满足控制变量的要求，同时考虑SMA丝的特点，模糊控制器应具有较高的灵敏度和较好的鲁棒性，本文选取结构简单的三角形隶属函数和梯形隶属函数进行模糊子集的定义。如图5所示，定义误差e(t)的模糊集(语言值)为负大，负较大，负中，负较小，负小，零，正小，正较小，正中，正较大，正大，用符号表示即NB，NLB，NM，NLS，NS，Z，PS，PLS，PM，PLB，PB；误差变化率ec(t)的模糊集为负大，负中，负小，零，正小，正中，正大，用符号表示即NB，NM，NS，ZE，PS，PM，PB；q(t)的模糊集为{零，小，中，大}，即{Z，S，M，B}。

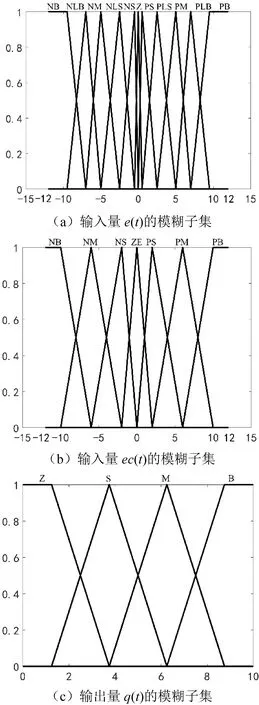
图5 模糊控制器中各变量的模糊子集

2.3 控制系统模糊控制规则设计

模糊控制规则是模糊控制器的核心，包括一系列“IF前件THEN后件”型的模糊条件句，其中前件和后件分别为模糊控制器的输入和输出的语言值。本文基于SMA的控制经验和实验观察，即基于操作人员的实际控制过程的方法建立模糊控制规则。具体建立思想如下：当误差e(t)为正且误差变化率ec(t)为负大或负中时，此时误差有快速减小的趋势，应降低输出量(控制量)，又由于SMA丝响应较慢，输出量不宜较小，所以输出量取较当前误差低一级的语言值；e(t)为正且ec(t)为正时，此时误差有增大的趋势，应增大输出量(控制量)，同时为避免系统产生较大超调，输出量不宜过大，所以输出量取较当前误差高一级的语言值；当e(t)为正且ec(t)为零或负小时，为使系统响应平稳，输出量取与误差同级的语言值；当e(t)为负时，此时系统已产生超调，应快速减小输出，由于当外部载荷基本恒定时且SMA驱动器的冷却过程为自然冷却时，若继续加热，系统超调量将会增加，所以输出量选取为Null，即停止对SMA丝加热。设计的控制规则如表3所示。

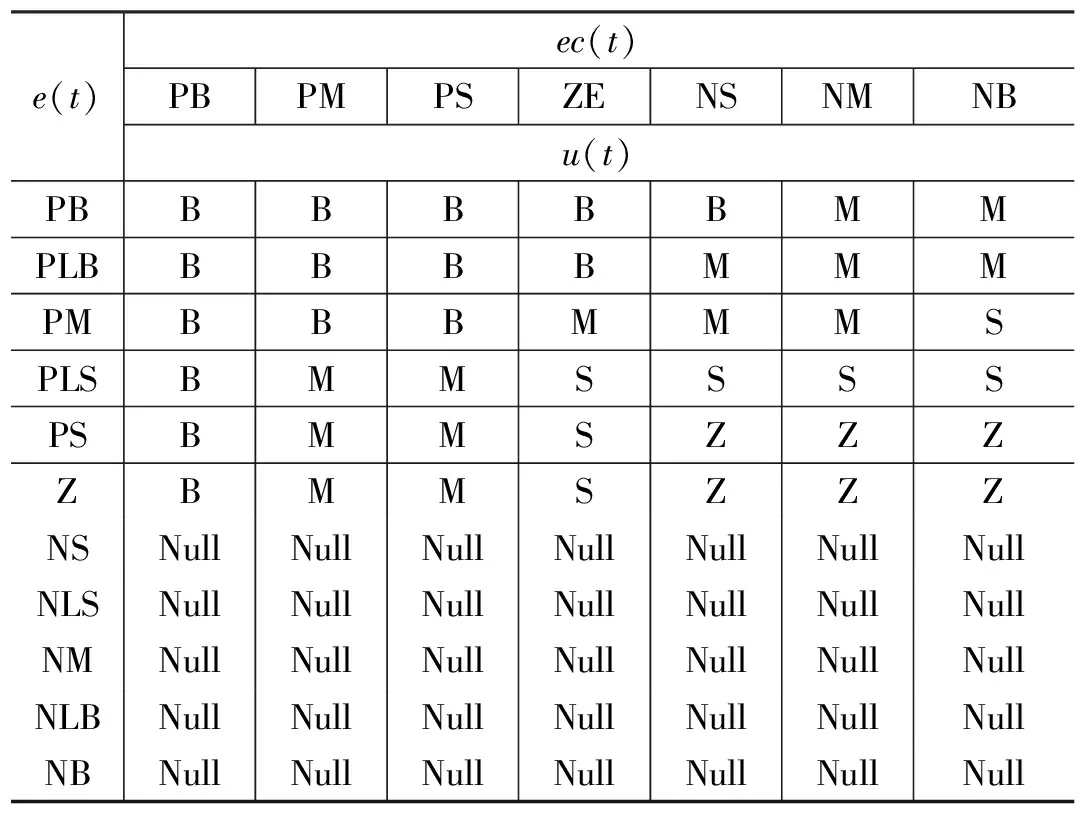
表3 模糊控制规则

2.4 模糊控制系统的解模糊

在模糊控制器中，控制量u(t)为模糊量，需经过解模糊获得清晰量q(t)后，才可输出至控制逻辑处理后进行控制。常用的解模糊方法有最大隶属度法、面积平分法和重心法等，其中重心法有效地计算了多个输出语言值之间的最佳折中，因此本文采用重心法进行解模糊，该方法首先计算输出变量范围内换算后隶属函数的面积，然后通过下式计算该面积的几何中心。

(5)

式中：u(t)为模糊推理决策的结果；f[u(t)]为对应隶属函数；umin，umax分别为q(t)当前语言值的范围。

3 SMA驱动器测控系统软硬件设计

在完成模糊控制系统原理性设计的基础上，需要选择和搭建控制系统硬件，并进行系统软件的设计。综合考虑测控系统实时性、输入输出通道的数量、控制方法计算量的大小，以及显示和数据存储的要求，进行了软硬件的设计和开发。

3.1 测控系统硬件结构

本文采用上下位机的测控系统方案，下位机采用NI公司的PXI控制系统和Linux操作系统，保证了多个角度传感器和温度传感器的信号以及PWM输出控制信号的实时性。系统中数据采集卡的具体参数如表4所示；测控系统原理如图6所示；搭建完成的控制系统如图7所示。

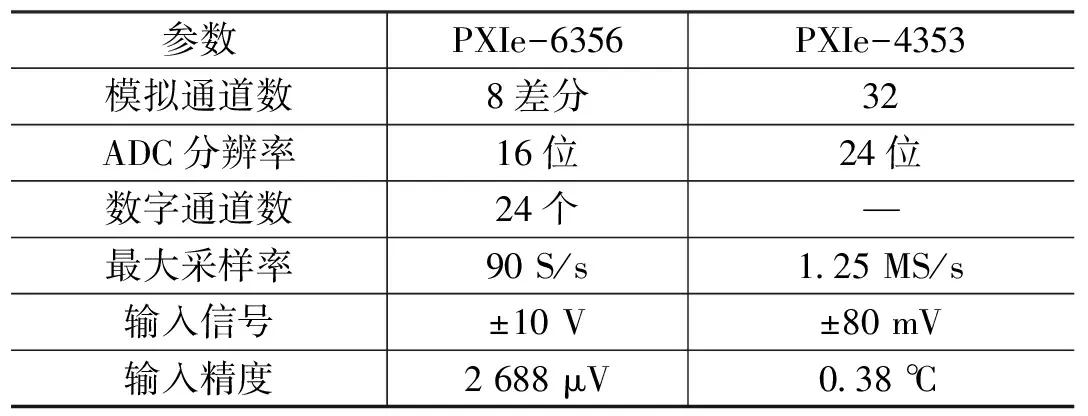
表4 PXI控制系统数据采集卡参数

图6 机翼后缘变弯度测控系统原理

图7 机翼后缘变弯度测控系统实物

PWM输出控制信号的频率为2 Hz，幅值为5 V，经过信号调理电路变换成同频率且幅值为10 V的PWM控制信号后输入固态继电器DD200D100的控制端，信号调理电路及SMA丝加热电路如图8所示。角度传感器选用北京齐开科技有限公司的QKJL-240霍尔传感器，测量范围0～240°，测量精度≤0.6°，输出信号为4～20 mA电流，经变送器WS15241转换为0～10 V电压信号后输入PXIe-6356采集。温度传感器为K型热电偶，具体参数：测量范围0～260 ℃，测量精度±0.3%，温度漂移±0.015%/℃。

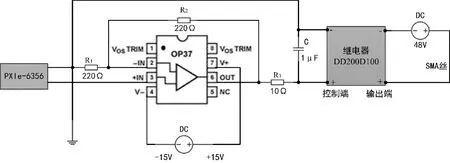
图8 信号处理电路及SMA丝加热电路

3.2 测控系统软件设计

测控系统软件在LabVIEW中完成，测控过程如图9所示。先进行系统初始化，并判断采集到的温度信号和角度信号是否正常。若无异常，对SMA丝预热，预热是通过施加占空比为2%的PWM信号对所有的SMA丝加热，保持SMA在30℃，以消除结构的间隙和外界温度及气流对SMA丝的影响。预热完成后，启动系统并根据各关节当前偏转角度误差和期望角度的符号判断应加热丝的方向和位置，实现SMA丝驱动器的差动控制。

图9 测控过程软件流程

4 机翼后缘偏转实验研究

SMA驱动机翼后缘偏转模型和测控系统制备完成以后，对其进行空载、静态等效载荷加载和亚音速风洞气动载荷加载实验。

4.1 模型地面空载实验

将后缘机翼模型固定在刚性实验平台上，空载情况下进行后缘变弯度功能实验，如图10所示。实验过程中后缘偏转角度随时间变化曲线如图11所示，共包括5个阶段：0～18 s为后缘结构由自然状态下的初始位置向上偏转至10°的阶段，即上侧SMA丝驱动器的加热响应阶段；19～31 s为10°稳定阶段，将后缘保持在上偏10°的状态不变；32～195 s为上侧SMA丝自然冷却阶段，此阶段中控制系统不工作；196～227 s为下侧SMA丝的加热响应阶段，机翼后缘向下偏转到-10°的位置；之后13 s为-10°稳定阶段。从图11中可以看出，在后缘向上偏转的过程中，系统的调节时间为18 s，无超调量；在后缘向下偏转的过程中，系统的调节时间为32 s，超调量为2.5%(0.25°)；实验过程中SMA丝的加热信号(PWM)的占空比随时间变化曲线如图12所示，后缘偏转至10°和-10°的状态如图13所示。从实验的结果可以看出，机翼后缘可以实现±10°的偏转。

图10 机翼后缘偏转地面空载实验

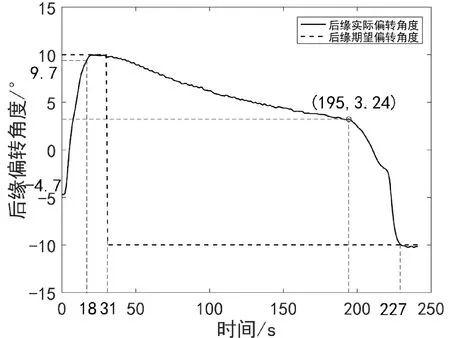
图11 模型地面空载实验中后缘偏转曲线

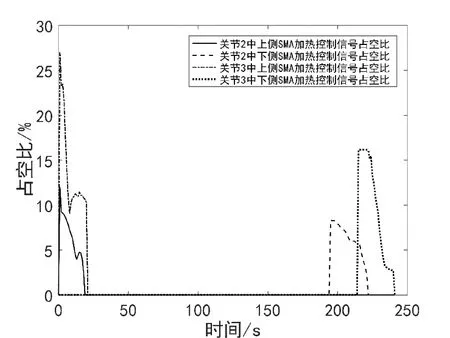
图12 模型地面空载实验中SMA驱动器加热控制信号的占空比曲线

图13 机翼后缘上偏10°和下偏-10°的状态

4.2 模型等效静态载荷加载实验

对机翼后缘结构采用施加等效集中载荷的方式进行静态加载，根据前期对机翼在0.7 Ma风速和8°迎角状态下的气动载荷仿真分析结果，设定载荷质量为6 kg，等效扭矩为7.2 Nm，为气动载荷扭矩的1.5倍。实验过程如图14所示，环境温度为28 ℃，实验过程中后缘偏转角度随时间变化曲线如图15所示。从图中可以看出，实验同样划分为5个阶段，在后缘向上偏的过程中，系统调节时间为21 s，超调量为9%(0.9°)；在后缘向下偏转的过程中，系统的调节时间为15 s，超调量为8.5%(0.85°)；实验过程中SMA丝的加热信号随时间变化曲线如图16所示。

图14 机翼后缘偏转静态载荷加载实验

图15 模型等效静态载荷加载实验过程中后缘变弯度曲线

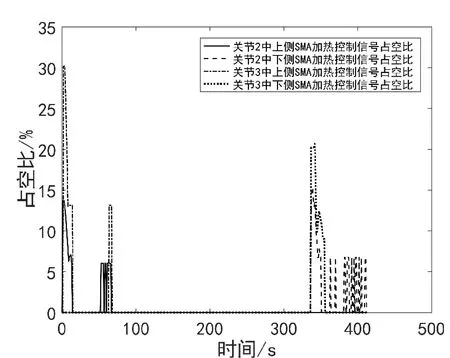
图16 模型等效静态载荷加载实验过程中SMA驱动器加热控制信号占空比曲线

与空载实验结果相比，在后缘向上和向下偏转的过程中，系统产生了一定的超调量，主要是由SMA丝变形过程中的相变潜热影响所致。实验结果表明，模型中SMA驱动器的驱动力矩能够克服气动载荷力矩，实现后缘±10°的偏转功能。

4.3 模型风洞载荷加载实验

实验在2.4 m×2.4 m的连续式风洞中进行，风洞中的周围环境温度始终保持在26°，风速0.7 Ma，机翼迎角为8°，将变体机翼通过机身固定于风洞侧壁，如图17所示。实验过程中后缘偏转角度随时间变化曲线如图18所示，偏转过程共分为5个阶段，向下偏转过程中，系统调节时间为22 s，超调量为0.7%(0.07°)；向上偏转过程中，系统的调节时间为33 s，超调量约为5.9%(0.59°)；实验过程中SMA丝的加热信号随时间变化曲线如图19所示。

图17 模型风洞载荷加载实验

图18 模型风洞载荷加载实验过程中后缘变弯度曲线

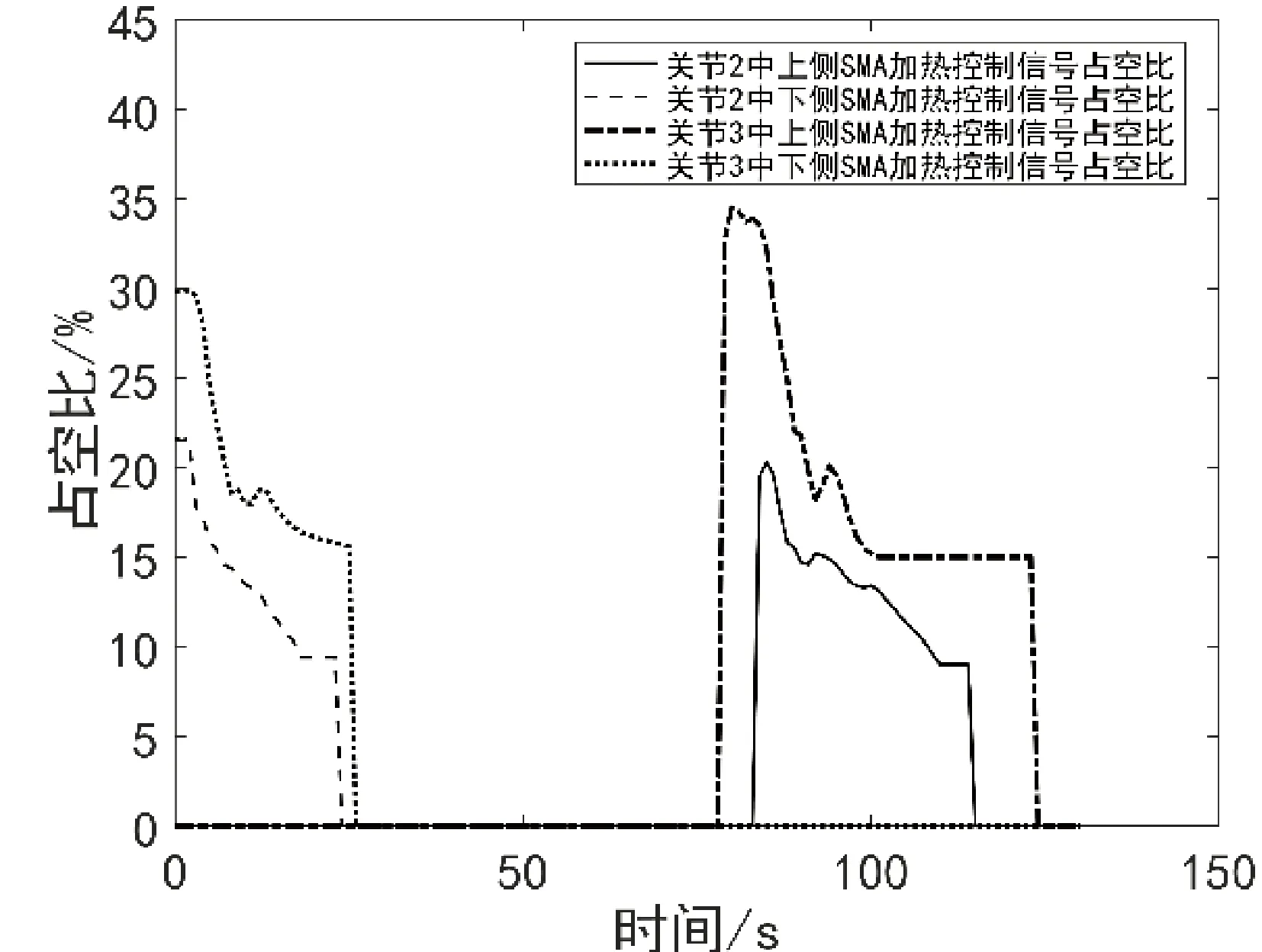
图19 模型风动载荷加载实验过程中SMA驱动器加热控制信号占空比曲线

在风洞载荷加载实验中，SMA丝驱动器实现了机翼后缘±10°的连续偏转，获得了理想的控制效果，实现了智能材料驱动器在风洞环境下对机翼结构的偏转变形。

5 结语

本文设计了SMA驱动的可变弯度机翼后缘结构，针对SMA差动驱动器具有强时变性和非线性的特点，设计了不依赖于数学模型的模糊控制器。搭建了基于LabVIEW和数据采集卡的测控系统。将模糊控制器应用在变弯度机翼后缘上，完成了变弯度机翼后缘的空载、地面等效载荷加载和风洞载荷动态加载偏转试验。实验结果表明，SMA丝驱动器能够实现对机翼后缘在0.7 Ma风速和8°机翼迎角状态下的连续偏转，稳态下的偏转角度误差小于±0.6°,超调量小于10%，采用的模糊控制方法基本实现了SMA驱动器的较精确控制。