滤光片阵列多光谱图像拼接与灰度调整算法

李铜哨， 孙文邦*， 赵汉东， 白新伟， 王志磊

(1. 空军航空大学航空作战勤务学院， 长春 130022； 2. 陆军勤务学院， 重庆 400050； 3. 93525部队， 日喀则 857000)

航空滤光片阵列多光谱相机同一时刻获取的数据为包含多个波段的窄带图像，需要对不同时刻获取的图像数据进行裁剪、拼接处理，才能得到单波段大区域图像。受机械快门影响，相机在不同时刻成像时的曝光量存在一定差异，导致单波段拼接图像容易出现具有一定宽度的明暗条纹，破坏了地物灰度一致性，影响了光谱图像后期处理及应用。因此，为满足滤光片阵列多光谱图像应用需求，必须解决滤光片阵列多光谱图像条带间存在的地物灰度差异。

目前，图像灰度校正算法大致可分为两种类型：一是在预处理阶段对图像进行校正，如Retinex算法[1-2]、Wallis算法[3]、直方图匹配算法[4]等；二是在图像拼接为全景图时，对重叠区域像素灰度进行融合，如渐入渐出融合[5]、加权平均融合[6]、弧函数权重模型[7]等。上述算法主要从视觉效果上消除图像灰度差异，而光谱图像灰度校正需要考虑校正前后地物光谱的保真度，尽可能避免光谱信息的损失。此外，Tian等[8]提出一种改进Wallis滤波方法，通过逐行/列计算图像行/列重叠区域像素灰度均值比，进一步将图像灰度调整为一致，但灰度校正过程属于强制改正图像灰度，并不适用于包含地物光谱信息的多光谱图像。为解决分视场多光谱图像的灰度差异，方秀秀等[9]提出灰度线性变换算法，通过同名点灰度计算图像灰度变换关系。但该方法的灰度处理效果依赖于同名点数量及分布，同名点数量少且分布不均时，灰度变换关系不一定能够准确反映条带图像间灰度变换关系。

因此，现提出基于各波段重叠区域灰度均值比的均值统调算法，利用加速稳健特征(speeded up robust features，SURF)算法对投影后图像进行配准，单波段图像重叠区域灰度平均值比的均值作为图像灰度调整系数，并以参考图像灰度为基准，依次对配准后图像灰度进行调整，以解决单波段多光谱拼接图像中的灰度差异问题，且最大限度减少地物光谱信息的损失。

1 滤光片阵列多光谱成像特点

滤光片阵列多光谱相机采用画幅式成像，其在电荷耦合元件(charge-coupled device，CCD)探测器前沿着垂直飞行方向放置一个镀有数个窄带带通滤光片的滤光板，获得多光谱图像。

1.1 图像几何特点

由于每个带通滤光片只能通过一个指定波长范围的图像，探测器被分割成若干个光谱带，各光谱带之间存在一定宽度的隔离带，以避免波段图像之间的相互干扰。通过平台的运动，可以获得某一区域内的多光谱图像数据，而大区域单波段多光谱图像则需要通过图像拼接的方式才能够得到，如图1所示。

图1中所示的是以波段2和波段6为例显示拼接过程。4个时刻t1、t2、t3、t4分别获得4幅含有8个波段的多条带图像，然后从4幅图像中裁切各波段条带图像，再拼接在一起形成单波段图像。

图1 滤光片阵列多光谱数据面阵处理Fig.1 Area array processing of filter array multi-spectral dataset

1.2 图像灰度特点

一般情况下，多光谱相机一次曝光就可以获得某一区域多个波段大区域灰度一致图像，如线性渐变滤光片式多光谱相机[10]、可调谐滤光片式多光谱相机[11]，但滤光片阵列多光谱相机一次曝光只能获得某一区域不同波段的窄条带图像，再通过裁剪拼接获得单波段大区域图像。

由于不同时刻成像时曝光量可能存在差异，获取的部分图像会偏亮(暗)。因此，经裁剪、拼接得到的单波段大区域图像可能存在条带状的灰度差异。例如，图1所示的t3时刻与t1、t2、t4时刻存在明显的曝光量差异，t3时刻成像总体上偏暗，则裁切拼接后的每个单波段图像中均出现较暗的条带。正是由于多光谱图像中可能存在的条带灰度差异，破坏了地物灰度一致性，破坏了地物目标的光谱特征信息准确度。

2 灰度差异调整

滤光片阵列多光谱图像灰度差异调整主要包括图像几何关系确定、图像灰度调整和图像拼接3个步骤。

2.1 图像几何关系确定

图像几何关系确定主要包括条带图像有效区域模板确定、图像投影变换和图像配准3个部分。

2.1.1 条带图像有效区域模板确定

以8谱段滤光片阵列多光谱相机为例，其多光谱图像数据如图2(a)所示。条带图像间存在过渡区域，如图2(a)中黄色框线区域和图2(b)中黑色区域。因此，需要计算各波段条带图像有效区域的4个顶点坐标，以构建多条带图像有效区域模板，如图2(b)所示。

图2 各条带图像有效区域Fig.2 Effective area of strip image

2.1.2 图像投影变换

滤光片阵列多光谱相机成像时除了记录图像数据外，还记录了成像时平台的姿态信息(俯仰角φ、翻滚角ω、航向角κ等)。因此，选择t1、t2、…、tn时刻的n幅序列多条带图像，并根据式(1)和式(2)对各时刻图像和对应的图像模板分别进行投影[12]。

(1)

(2)

式中：X、Y为投影后像点坐标，像素；H为航高，m；D为投影后图像地面空间分辨率，m；x、y为条带图像上像点坐标，mm；f为相机焦距，mm；a1、a2、a3、b1、b2、b3、c1、c2、c3由式(2)计算得到。

2.1.3 图像配准

当多光谱相机成像时记录的平台姿态信息精度足够高时，投影变换后的图像在空间上只有平移关系。但是，由于平台姿态信息均存在一定的误差，若利用平台姿态信息进行投影后图像直接进行拼接处理，则拼接图像中很容易出现地物未对齐的现象，如图3所示。

从图3中可以看出，拼接缝处的地物存在明显错位，如图中红色虚线圆圈区域。因此，通过提取投影后图像间的匹配点，并且通过匹配点坐标计算单应性转换矩阵H，对图像进行配准处理。主要步骤如下。

图3 偏移量拼接图像Fig.3 Offset stitching image

步骤1匹配点提取。目前文献中，匹配点的提取算法较多，例如，SIFT算法[13]、SURF算法[14]等。

由于同一区域的各单波段条带图像需要由多张滤光片阵列式多光谱序列图像经裁切、拼接得到，处理的数据量较大。利用SIFT算法虽然能够提取亚像素级的特征点，但特征提取与匹配的耗时过长[15]。因此，现采用运行速度较快的SURF算法完成特征提取和匹配，通过RANSAC算法筛选出高精度匹配点[16]。

步骤2转换矩阵计算。设图像I0匹配点坐标为(X1,Y1)、(X2,Y2)、…、(Xn,Yn)，图像I1的匹配点坐标为(x1,y1)、(x2,y2)、…、(xn,yn)，则图像I1向图像I0的坐标转换为

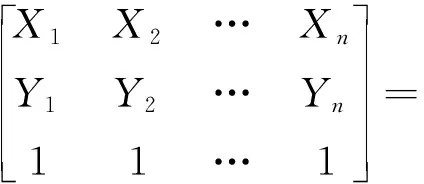
(3)

令

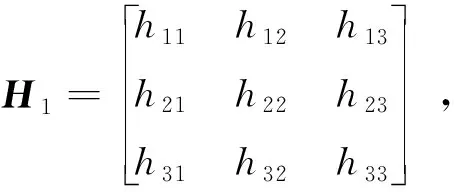
则式(3)可写为

P0=H1P1

(4)

故图像I1向图像I0坐标转换矩阵H1为

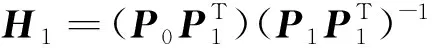
(5)

同理可得，图像I0向图像I1坐标转换为

(6)

步骤3空间位置确定。图像拼接过程如图4所示。首先确定基准图像I0，利用图像I1匹配点坐标P1和图像I0匹配点坐标P0，通过式(5)计算图像I1向图像I0的单应性转换矩阵H1，再通过式(4)计算图像I1在图像I0坐标系下的坐标，确定二者之间的位置关系。

图4 全局矩阵配准图像Fig.4 Global matrix alignment image

再通过类似方法，运用式(7)计算图像I2在图像I1坐标系中坐标，公式为

P1=H2P2

(7)

再将式(7)代入式(4)中可以计算得到待拼接图像I2在基准图像I0坐标系中坐标，如式(8)所示，可以确定图像I2与图像I0间的位置关系，表达式为

P0=H1H2P2

(8)

类似地，若有n张待拼接图像，则第n张待拼接图像In与基准图像I0间的位置关系为

(9)

由于采用单应性转换矩阵进行配准处理，存在误差积累效应，并且随着拼接数量增加，拼接图像畸变会越来越明显[17]。

故为减小图像拼接过程中畸变，选择序列中间图像为基准，采用两边向中间拼接的策略，如图5所示。

设图5中基准图像I0右侧有n张待拼接图像(I1,I2, …,In)，第n张待拼接图像In与基准图像I0间的位置关系如式(9)所示。

设基准图像左侧有m张待拼接图像(I′1,I′2, …,I′m)，左侧图像坐标矩阵设为P′i，坐标转换矩阵为Ti，与右侧转换矩阵计算式(4)类似，可以得到左侧待拼接图像I′1向基准图像I0坐标转换为

P0=T1P′1

(10)

则左侧第m张待拼接图像I′m与基准图像I0间的位置关系为

(11)

从图5可以看出，采用两侧向中间基准图像进行配准处理，则可以明显减少配准误差的积累效应。

图5 图像转换矩阵计算Fig.5 Image conversion matrix calculation

2.2 图像灰度调整

图像灰度调整主要依据条带图像重叠区域的灰度进行调整，涉及关键技术主要包括条带图像重叠区域确定、灰度调整系数计算、调整图像灰度3个方面。

2.2.1 条带图像重叠区域确定

以相邻两幅相邻的多光谱图像为例。首先，利用成像时平台姿态信息对多光谱图像和对应的模板均进行投影变换；然后，利用计算得到的坐标转换矩阵Hi(或Ti)对投影后多光谱图像和模板与基准图像的进行配准，模板与基准图像配准后的位置关系如图6(a)、图6(b)所示。提取单波段图像重叠区域时，只保留模板图像中对应波段区域，如图6(c)、图6(d)所示的为第一波段模板区域图像。将相邻的转换后的模板图像相乘，得到相应波段重叠区域模板，如图6(e)所示。

图6 图像重叠区域模板Fig.6 Image overlay area template

然后，将重叠区域模板分别与两幅配准后多光谱图像相乘得到单波段的重叠区域图像。以第一条带图像为例，如图7所示。图7(a)、图7(b)分别为配准后的第1、2幅多光谱图像，图7(c)为第1、2幅中第1波段的重叠区域图像。

图7 重叠区域图像Fig.7 Image of overlapping area

2.2.2 灰度调整系数计算

灰度调整系数计算方式较多，例如文献[8]针对滤光片阵列多光谱图像提出灰度线性变换算法，核心思想是分别选择各波段重叠区域匹配点的灰度均值比，作为待拼接图像各波段的灰度调系数。但该方法灰度处理效果依赖于同名点的数量及分布，同名点数量少且分布不均时，灰度变换关系不一定能够准确反映条带图像间灰度变换关系。

故采用重叠区域灰度均值比的均值作为各波段统一的调整系数。设图7(c)、图7(d)分别是相邻第i和第j两幅图像中第1个波段的重叠区域图像，可以分别计算该重叠区域图像的灰度均值ki1、kj1。同样，可以计算得到其他7个波段的灰度均值，每幅图像分别可以得到8个均值，即ki1、ki2、ki3、ki4、ki5、ki6、ki7、ki8和kj1、kj2、kj3、kj4、kj5、kj6、kj7、kj8。则可以通过式(12)计算得到第j幅图像的灰度调整为第i幅图像灰度的调整系数gij，即

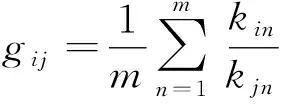
(12)

式(12)中：m为波段数。

2.2.3 调整图像灰度

求出图像灰度调整系数gij后，就可以对投影后图像进行灰度调整，以9幅多光谱图像为例，选择中间的第5幅图像为基准，依次将各灰度调整系数与对应序列图像中的每个像素灰度相乘。各灰度调整系数计算公式为

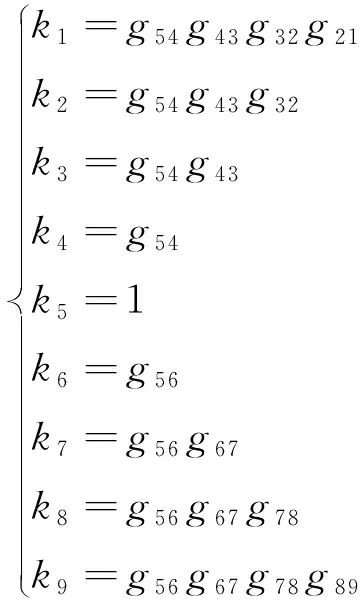
(13)

2.3 图像拼接

滤光片阵列式多光谱图像拼接不同于其他图像，图像拼接前需要提取各单波段条带图像，如图8所示。首先提取各单波段图像在配准后的图像模板上对应区域，即构建配准后图像对应的单波段图像模板，并将配准后的图像与各单波段图像模板相乘，得到单波段配准后图像。最后，对各单波段条带图像进行拼接，得到灰度一致的滤光片阵列多光谱单波段图像。

图8 单波段图像拼接Fig.8 Single-band image stitching

3 实验与分析

为了验证灰度调整算法的可行性，采用某航拍无人机滤光片阵列多光谱相机拍摄某地区的多光谱图像数据进行验证实验。其中，部分多光谱图像如图9所示。

图9 实验图像Fig.9 Experimental images

未进行灰度处理和本文算法处理后的单波段多光谱图像如图10所示。

图10 灰度调整对比图Fig.10 Grayscale adjustment comparison chart

由图10可知，未进行灰度处理的单波段拼接图像整体灰度不均匀，同一区域中的地物存在着较为明显的灰度差异，如图10中箭头所指位置。而本文算法处理后的单波段图像灰度整体比较均匀，不存在明显的灰度差异，说明本文方法较好地解决了条带图像灰度不均的问题。

为进一步说明本文算法的有效性，使用文献[9]中灰度一致性校正算法与本文算法进行对比实验。文献[9]与本文算法处理后的各单波段图像如图11所示，对比图像分别为3波段、4波段、5波段、7波段多光谱图像。

从目视效果上看，图11(g)和图11(h)整体灰度均匀，无明显的灰度差异，说明对比算法能够解决图像灰度不均匀问题。但图11(f)中地物灰度不均匀问题有所改善，并未完全解决灰度不均匀问题。而本文算法处理后图像无明显的灰度差异，而且与灰度未调整图像差异较小。

图11 灰度调整后效果对比Fig.11 Comparison of the effect after grayscale adjustment

对于第2波段图像，由于无法提取匹配点，文献[9]无法进行灰度调整；对于第4波段图像，由于部分相邻图像匹配点数量较少，灰度变换模型无法正确反映匹配点对应图像灰度的变化关系，调整后图像仍存在灰度差异，部分第4波段图像的匹配点分布如图12所示。

图12 第4波段匹配点分布Fig.12 Distribution of matching points for 4th band

此外，对比算法调整后的第7波段图像中图像上方较图像下方灰度明显偏亮，经分析发现，使用RANSAC算法筛选出的精匹配点具有随机性[18]，基于匹配点灰度值计算出的灰度变换模型系数可能存在一定差异，影响了条带图像灰度的正确调整，如图13所示。

图13 灰度调整后局部放大对比图Fig.13 Grayscale adjusted partial comparison

因此，当重叠区域图像存在提取匹配点数量少、匹配地分布不均匀时，对比算法无法解决单波段图像灰度不一致问题。此外，匹配点处的灰度值直接影响了图像灰度变换关系参数，不一定准确反映相邻图像间的灰度变换关系。而本文算法处理后单波段图像灰度分布均匀，图像灰度不一致问题得到较好的解决。

为进一步说明本文算法的性能，分别计算调整后各单波段条带图像重叠区域灰度平均值的差值来说明，如图14所示(仅显示3、4、5波段图像)。

图14横坐标是图像幅序号，纵坐标是重叠区域平均灰度差，灰度级为0～255。由图14可知，文献[9]处理后部分单波段条带图像重叠区域灰度均值的变化剧烈，说明调整后单波段图像部分区域仍存在较明显灰度差异。

图14 重叠区域灰度均值差值对比Fig.14 Difference in mean grey value of overlapping areas

总体上看，本文算法处理后的重叠区域灰度差值要小于文献[9]。经分析可知，对单波段图像进行灰度调整时，当重叠区域匹配点数量较多时，文献[9]可以取得较好的灰度调整效果。但由于各单波段图像调整时选择的参考图像不是同一时刻获取的图像数据，灰度调整后的图像灰度存在偏暗(亮)的现象。

而本文算法处理后的图像重叠区域平均灰度差未处理图像整体较小，各波段重叠区域灰度差整体近似一条直线，不存在部分条带图像重叠区域灰度差突变的情况。本文算法处理后的各单波段图像与参考图像的灰度近似一致，较好地保持了地物在不同波段下的光谱反射特性。

由此可知，提出的基于重叠区域图像的灰度调整算法，充分利用了重叠区域图像的灰度信息，调整后的各单波段图像灰度均匀，有效解决了单波段图像中灰度不一致问题。

4 结论

针对滤光片阵列式多光谱图像灰度不一致的问题，提出了一种基于重叠区域的图像灰度调整算法，即根据各个波段图像重叠区域灰度均值比的平均值，对图像数据中各波段统一进行灰度调整，调整后的拼接图像对齐效果较好、同一地物灰度一致，降低了对图像处理中特征提取与匹配的影响。通过实验对比，表明针对滤光片阵列多光谱图像提出的灰度调整算法较目前算法有较强的适用性和较好的灰度处理效果，有效解决了滤光片阵列多光谱图像中的地物灰度不一致问题，能够满足多光谱图像的后期处理及应用需求。