基于智能馈线终端和行波时差的故障定位技术研究
2022-02-02万德春但富中王淑艳葛佳盛
费 阳,万德春,但富中,王淑艳,葛佳盛
(国网电力科学研究院有限公司,江苏 南京 210000)
0 引言
配网是电力系统中与用户直接接触的部分,同时也是电力系统中最容易发生故障的部分,配网稳定运行直接影响用户的用电体验。在配网故障发生时,能够快速准确地定位故障点,能够提高用电用户的满意度,降低电网的维护成本,减少因长时间停电导致的损失,对于整个输电系统稳定、安全运行具有重要意义[1-5]。
配网结构十分复杂,大部分馈线都有许多分支线路,造成三相不是标准的对称形式,对故障定位信息分析产生很大影响,且许多配网的线路长度较短,对定位精度要求更高。目前主流的配网故障定位方法主要有阻抗法、注入法和行波法[6-10]。文献[11]通过计算配网阻抗算法进行故障定位,由于该方法没有考虑到配网复杂结构导致的电流和电压传输特性异常、配网三相不是标准的对称等情况,这些因素严重地影响定位精度,同时配网复杂的分支线路在很多工况下可能导致阻抗法发生误判。注入法[12]是利用线路的某一相发生接地短路时短接原边。此时,故障相的电压互感器向接地点处发射一个电流信号,该信号会从接地点处流入大地,然后通过跟踪该信号就可以确定故障的相别并找出故障点,实现故障点的定位,但连续性接地电弧和过渡电阻会对该方法产生干扰,不适用于实际配电线路。行波法[13-15]是近年来的研究重点,在配网故障定位中行波法已经被应用。目前应用较多的是基于单端行波法进行定位,该方法安装的设备较少,同时进行故障测距也较为简单稳定,但是由于行波的特性,在配网有大量分支的情况下行波会进行不断反射和折射,导致识别波头和反射波十分困难。文献[16]通过线模和零模行波传播时间差值对故障距离进行计算,该种新型的单端行波测距方法对行波的传播速度要求非常精确,不适用于配网中的混合电缆线路。
文献[17]提出一种针对只有单一结构配网的故障行波测距方法,利用行波频率特征进行故障距离计算,该算法主要依靠行波的频率特征区分度,对于复杂的配网结构,其行波频率成分混叠严重无法有效区分;基于双端行波定位算法[18-21]是通过行波到达两端设备的时间差和波速计算出故障到两端的距离,但是只适用于主干线上故障距离的计算,面对配网中众多支线的故障也难以精确测量;文献[22]提出一种多端法,将行波接受装置在每个支线的首位端都进行安装,每台装置都进行同步测量,根据行波到达的时间差进行故障距离的计算,该算法对于时间精度要求非常高,若存在微小的误差时会导致定位结果误差很大,所以在实际应用中存在一定的局限性。上述方法都是针对单一结构的线路,无法应用于混合电缆-架空线路。
本文通过各支线与主线的节点和末端的智能FTU检测的零序电流和零序电压信息进行故障区间定位,然后根据内置的行波采集模块检测故障行波波头分别到达故障区间两端设备的时刻差进行故障点精确定位。利用杆塔定位方式避免行波波速和线路长度的变化对定位精度的影响,增加了定位精度。
1 基于FTU判断故障区间
由于配网自动化的不断发展,FTU 设备被大量地应用到配网线路中,该设备可以检测线路的相电压、电流和零序电压、电流。根据配网接地故障时刻的零序电压和零序电流特征就可以确定故障点在两个检测点之间,则确定了故障区间。
针对中性点不接地系统的线路,如图1所示,在线路中O 点发生接地故障,则类似于一个零序电压源在O 点接入,该零序电压源可以使得线路产生零序容性电流。由于中性点不接地系统线路零序网络主要为线路对地电容组成,所以线路中的零序电流为容性电流,故障时刻线路中各支路的零序电流方向如图1所示。

图1 故障线路的零序电流方向Fig.1 Zero-sequence current direction of the faulty line
上述分析可知,针对中性点不接地系统的故障区间判断方法为:
1)故障支线判断。分支线路运行情况正常时,零序电流超前零序电压90°;若零序电流滞后零序电压90°,则表明该支线发生故障。
2)故障区间判断。依次比较故障支线上各FTU采集的零序电压和零序电流,若检测到一个检测点的零序电流滞后零序电压90°,另一个相邻检测点的零序电流超前零序电压90°,则故障区间为两个检测点之间。
针对中性点经消弧线圈接地系统线路如图2所示,该接地方式使得消弧线圈能够对线路的电感电流起到补充的效果,导致线路正常情况下零序电流超前零序电压90°,所以故障时线路零序电流方向如图2所示。
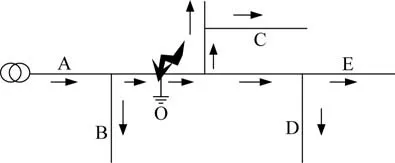
图2 故障线路的零序电流方向Fig.2 Zero-sequence current direction of the faulty line
此时零序电流和零序电压的相位差难以确定故障区间,需要根据残流增量原理进行故障区间定位,调整消弧线圈的脱谐度产生故障接地时的残流增量,由于电感电流的方向是从电源流向接地点,所以发生故障时线路上的零序电流会有一定的变化,但故障下游线路上的零序电流不会变化。该方式需要注意故障为经电阻接地时,若调节消弧线圈会导致零序电压幅值发生变化,需要对应地将零序电流进行调整。
根据上述分析可知,中性点经消弧线圈接地系统线路的故障区间判断方法为:
1)故障分支判断。故障发生时调整消弧线圈,若调整前后线路零序电流没有任何变化,则为故障分支;若调整前后,该分支线路零序电流发生变化,则为正常分支。
2)故障区间判断。故障发生时依次检测线路上各FTU 采集的零序电流,若相邻FTU 的零序电流变化较大,则故障区间在两个检测点之间。
2 行波法故障定位
根据行波原理,若线路发生故障,线路由于运行状态的变化会产生暂态电压和暂态电流,暂态信号会以故障点为中心向两端传播,依据该原理可以通过行波信号的检测、分析和计算实现对故障的精确定位。行波法定位关键在于行波波速、波头识别和线路长度,这些因素对定位精度影响较大。
2.1 双端行波故障定位原理
行波法主要根据故障发生时行波波头到达两端设备的时间差来计算出故障点,两端FTU 设备能够实现时钟同步和GPS 定位,分别记录行波波头到达两端FTU的时刻,行波测距原理如图3所示。

图3 故障测距原理图Fig.3 Schematic diagram of fault ranging
设确定的故障区间为单一线路,线路长度为L,行波在两个FTU 之间的传播速度为v。故障区间两端FTU记录的行波波头到达时刻分别为tM、tN。
故障点距离M端的距离计算公式

根据式(1)、式(2)可知,只要准确得到故障行波波头到达两端的时刻,就可以进行故障点精确定位。
2.2 行波波头检测算法
小波变换[23]由基小波的伸缩和平移组成的函数组合ϕa,b=|a|-1/2ϕ[(t-b)/a],其中ϕ(t)表示基本小波函数,a表示尺度因子,b表示平移因子。将信号进行小波变化的公式为:
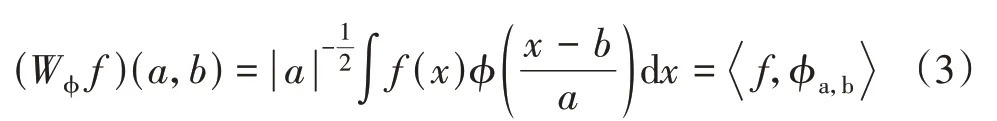
a= 1/2j,则ϕa,b=|a|-1/2ϕ[(t-b)/a]称为二进小波,利用二进小波进行的变换称为信号的二进小波变换。由a的数值可知,二进小波可以避免信号分解时的重叠现象,且仅对尺度进行改变,但是平移参数没有变化,所以二进小波变化在平移上具有一致性,该特性使得它对于一些奇异值的检测非常灵敏。利用二进小波变换的模极大值来检测信号中的奇异值。小波模极大值是信号f(x)进行小波变换,一定的尺度S下,在x∈(x-δ,x+δ)中|WSf(x)|≤|WSf(x0)|则x0表示在S尺度下的小波变换模极大值点,WSf(x0)为小波变换模极大值。
通过小波变换可以得到连续信号在相应位置的变化率情况,根据小波变换模极大值点可以得到信号中变化率最大的点位置,恰好故障行波的波头就是整个故障行波中变化最大的点,所以应用小波变化可以准确地找出故障行波波头,从而得到波头到达测量点的精确时刻,为后续的故障定位奠定基础。
2.3 杆塔定位
杆塔可以看作将线路近似均匀等分的节点[24],如图4 所示,杆塔之间的连接线与配电线路长度是呈一定比例的,故障点距离占线路长度的百分比与杆塔数量之间存在一定的关系。在安装设备时可以根据杆塔之间的直线距离,判断各杆塔线路长度占总线路长度的百分比,根据该方式可以将各杆塔进行编号制作表格。当发生故障时,可以由故障定位算法计算出故障点,然后再通过表格找到故障附近杆塔,快速找出故障点的地理位置。

图4 杆塔分布示意图Fig.4 Schematic diagram of the distribution of pole towers
由于实际线路受温度[25]、负荷波动[26]等因素的影响,很难准确估计线路长度,该方法只要确定故障附近杆塔号,就可以知道故障点的直线距离,该距离是固定不变的,方便线路运检人员进行巡检[27],大幅降低了线路长度精确性对故障点位置的影响,在实际应用中更加具有实用性。
3 试验验证
3.1 基于FTU的故障区间定位试验
为验证智能FTU和行波信息应用于故障精确定位的可行性,搭建了智能FTU行波动态增补实验环境,如图5 所示,主要实验设备有PF1000A 暂态电流输出装置、PF 系列配线故障指示器检测平台、行波采集装置和PH02型行波测距校验仪,现场实验设备环境如图5(a)所示。在PF系列配线故障指示器检测平台设置线路参数,线路全长10 km,接地点位于距离小号侧2 km位置处,线路首末各安装智能FTU 设备,如图5(b)所示为实验线路结构示意图,接地电阻设置为0 Ω、50 Ω、100 Ω、500 Ω、1 000 Ω,分别监测不同接地电阻下,行波的形态特征变化及FTU监测故障的能力。
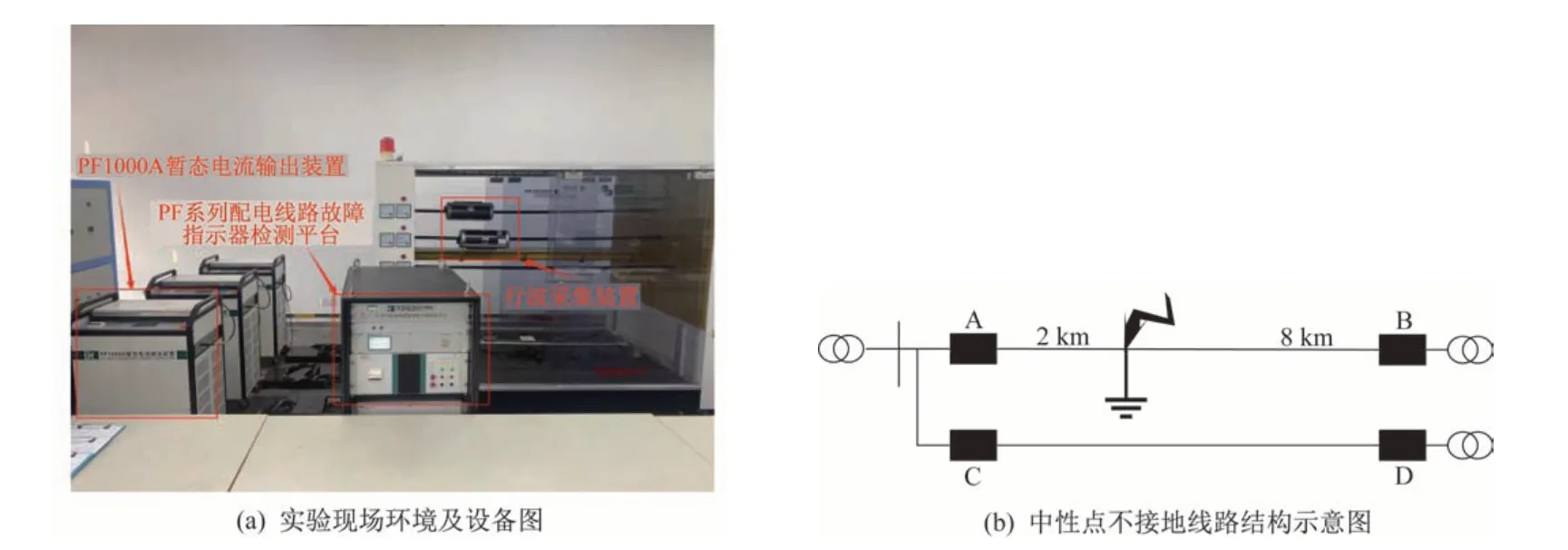
图5 实验装置及设备安装位置图Fig.5 Experimental apparatus and equipment installation location diagram
设置中性点不接地系统配网试验线路在FTU-A和FTU-B之间发生单相接地故障,观察安装在线路上的智能FTU设备检测的零序电压和零序电流的变化特征,为验证上节提出的相位差理论,将零序电流和零序电压的幅值进行对齐,如图6所示。
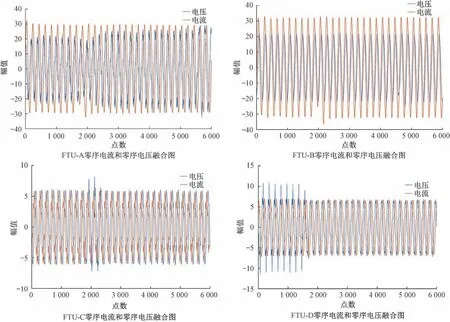
图6 中性点不接地系统线路故障各智能FTU检测的零序电压和零序电流幅值对齐后的融合图Fig.6 Fusion diagram of the zero-sequence voltage and zero-sequence current amplitude detected by each intelligent FTU for line fault of neutral point ungrounded system
由图6 可知,在故障点前FTU 检测到的零序电流超前零序电压90°,故障点后零序电流滞后零序电压90°,在无故障线路上所有FTU检测到的零序电流都超前零序电压90°,验证了上节提出的针对中性点不接地系统线路利用零序电流和零序电压相位来进行故障区间定位的可行性。
设置中性点经消弧线圈接地系统配网试验线路在FTU-A 和FTU-B 之间发生单相接地故障,如图7 所示。观察安装在线路上的智能FTU设备检测零序电流的变化特征,为验证上节提出的零序电流变化理论,将所有FTU 故障时刻检测到的零序电流进行对比,如图8所示。
图7 中性点经消弧线圈接地线路结构示意图Fig.7 Structure diagram of the grounding line at the neutral point through arc suppression coil
由图8 可知,中性点经消弧线圈接地系统线路发生单相接地故障时,正常支线上的FTU 检测到的零序电流不会有大的变化,对应的故障支线上FTU 检测到的零序电流会发生变化,FTU-A 零序电流会增大,FTU-B 零序电流变化不大,故障点在两者之间,即故障区间。
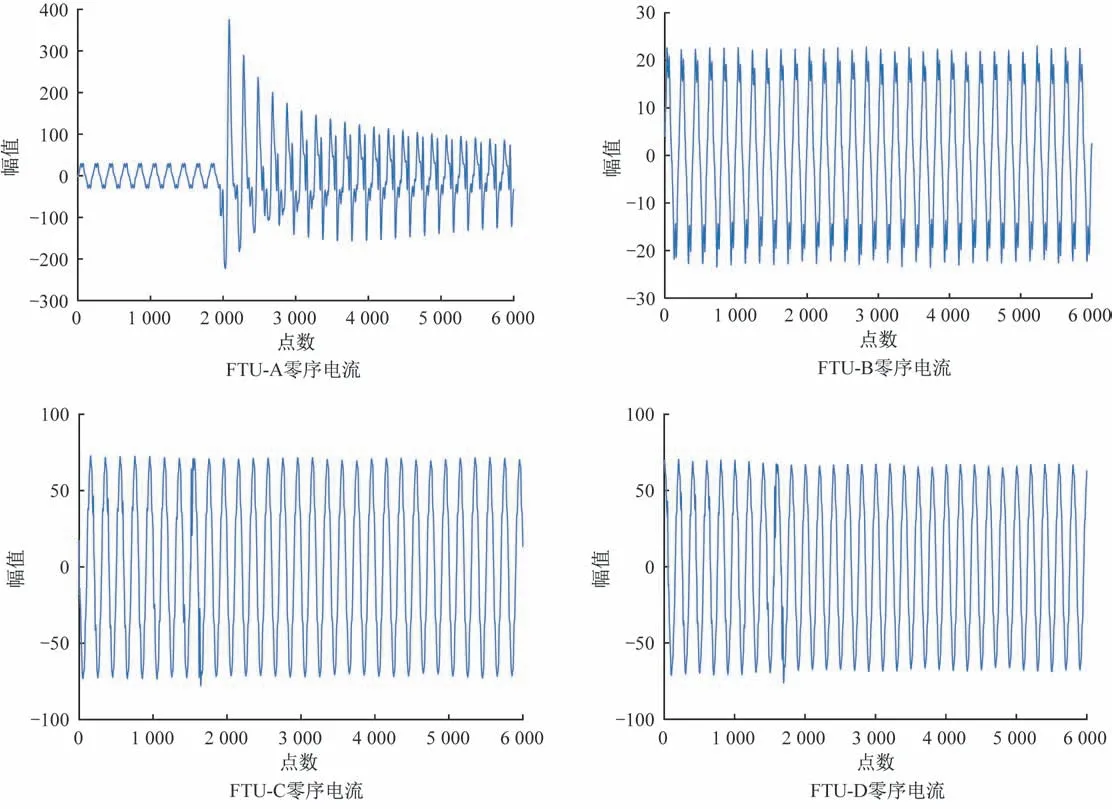
图8 中性点经消弧线圈接地系统线路故障零序电流变化图Fig.8 Zero-sequence current change diagram of grounding system line fault at neutral point through arc suppression coil
3.2 基于FTU行波故障精确定位试验
在中性点不接地系统线路中验证行波时差对故障位置的精确定位试验,FTU-A和FTU-B分别表示M侧和N 侧,设线路MN 中距离母线M 侧2 km 处发生单相接地故障,接地电阻R= 100 Ω,两侧母线端的具有行波监测能力的FTU 采集到故障相行波,经过连续小波变换后如图9所示。可以发现行波波头位置处的变化量最大,到达两端MN 时有明显的异常突变信号。计算其连续小波变换后的模极大值起始突变时刻分别为t1= 41 116 μs、t2= 41 125 μs。
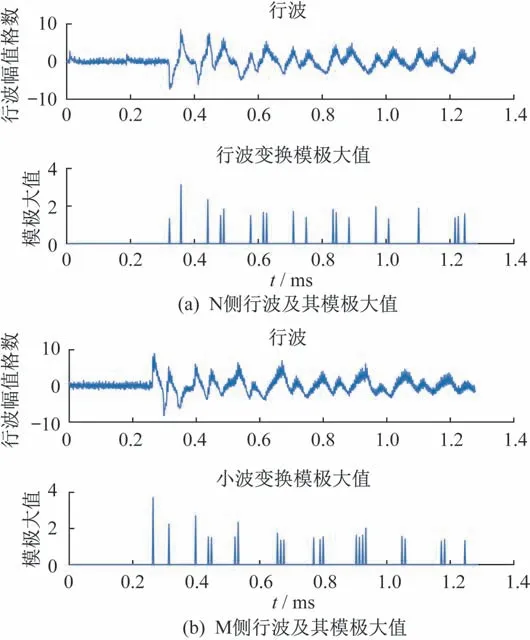
图9 两侧故障行波及模极大值Fig.9 Fault traveling wave and modulus maximum value on both sides
因为故障点距离母线M 侧较近,所以行波波头最先被M侧的设备监测到,根据准确识别行波波头来精确定位故障点。计算两端同步设备监测的行波波头时间差值,计算的故障点距离M侧母线端L=2 082.93 m,计算结果较为精确。
为验证不同接地电阻故障下的定位结果,为进行不同接地电阻下,监测到行波的幅值、时间差、定位距离等参数的汇总表,如表1所示。

表1 不同接地电阻行波参数汇总表Table 1 Summary table of traveling wave parameters of different grounding resistors
通过表1可知:
1)接地电阻越大,行波幅值越小;
2)利用行波监测单相接地故障,接地电阻为1 000 Ω时行波仍然有较明显的特征。因此,基于行波的单相接地监测耐过渡电阻能力≥1 000 Ω;
3)小波变换识别行波波头在高阻接地时仍然具有较好的应用效果,可以准确识别波头位置;
4)由于行波波形形态存在差异,行波定位存在一定误差,但FTU总体最大误差不超过±300 m。
4 结语
本文提出一种基于智能FTU行波监测模块信息的故障定位方法,该方法可以有效降低波速和线路结构对故障诊断精度的影响,适用于配网中的电缆-架空线路,解决了形态不好的故障行波波头难以识别的问题,同时建立快速识别故障区间和杆塔定位机制。通过仿真验证得到以下结论:
1)通过零序电流与零序电压的相位特征和零序电流的变化,对不同中性点接地系统线路故障区间进行定位,使得故障区间定位算法能够适用更多不同类型线路,增强了该方法的适用性。
2)利用故障行波中的突变分量消除了波形中谐波对波头的影响,通过小波变换模极大值得到故障行波波头的精确位置,再通过故障点距离与线路总长的比值应用到杆塔定位中,经过仿真验证了该方法的准确性。
