计及输电通道容量约束的中长期发电计划

张水平，付聪，左剑，王一鸣，郭瑞鹏

（1.广东电网有限责任公司电力调度控制中心， 广州 510030；2.浙江大学电气工程学院， 杭州 310027）

0 引言

随着电网规模和交换容量的不断增加，输电断面安全的重要性日益突出，特别是区域间的输电通道往往成为电网安全运行的薄弱环节［1］。当输电断面存在功率过载时，需要及时采取措施消除线路越限，包括调整机组出力、网络重构和切负荷等［2］。而在电网安全约束、电力市场和碳排放权市场等因素的相互影响下，调度员控制输电断面潮流的难度不断增加，给电网的安全运行提出了新的挑战［3-7］。在保证输电断面安全性的各项措施中，调整机组出力对电网的冲击和对用户的影响最小，是最常用的控制手段［8］，对保证电网安全稳定运行和提升智能调度水平具有重要意义。

对发电计划的研究多侧重于从日前到实时的发电计划［9-12］，而对中长期发电计划的研究则集中于水电或火水风联合调度［13-15］。文献［16］研究了检修计划中长期水火电联合优化调度的影响，但模型规模偏大，需要牺牲计算时间或精度。文献［17］考虑了日电量平衡和断面日交换电量校核，并非电力安全校核，对潮流越限的风险难以发现。文献［18-19］提出了多目标协调优化调度模型，给出帕累托前沿和最优折中解，以满足当前电网的综合运行要求。文献［20］提出了年度发电计划和检修计划的联合优化模型，为降低模型规模而大量减少了计算时段，导致无法准确计算发电量而需开展电量估算。

有研究进一步考虑了输电通道约束对发电计划的影响。文献［21］讨论了因传输线路或断面潮流阻塞导致的机组备用容量无法有效输出的问题。文献［22］在模型中引入输电通道的月度传输电量作为决策变量，但未涉及通道容量造成的限制。文献［23］从输电通道暂态稳定限额的角度分析了主要影响因素，并形成制定发电计划的若干原则，再在此原则的基础上依次完成各电厂内的组合优化。文献［24］在模型中计入了断面输电安全约束，并采用电网聚合的方式简化电网结构、提高模型求解速度，而实施聚合的前提是明确电网各机组的详细技术参数。此外，上述研究在遇到计算规模过大时，往往采取近似或预测的方法，对计算结果的精度或准确度有影响［13，16，20，22］；亦有研究未经过大规模电网算例的检验［9，18-19，23］。

本文基于中长期检修计划研究相应的发电计划优化方法。首先讨论各输电线路容量的限制在正常运行状态和故障情况下对机组出力的制约，并据此构造确定运行方式下的机组出力优化模型，旨在满足各项约束的情况下提升关键断面的传输效率。在缩减模型规模时仅消除冗余约束，不会对优化结果的精度产生影响。之后，将该优化模型与检修计划相结合，形成与之相适应的中长期发电调度方案。最后通过某省级电网的实际算例验证所述方法的有效性。

1 输电通道容量约束下的机组出力限制

在电网各运行方式下，多数机组的实际出力不会达到其容量值。有多种因素导致了对机组出力的限制：1）用于应对负荷波动和新能源出力波动而预留的备用容量；2）因发电资源不足而限制了最大出力，对于水电厂表现为来水量不足、因防洪需要产生的弃水等，对于新能源电厂表现为风力不足、光照不足等；3）固有的电量消耗，如厂用电和供热造成的容量减扣；4）市场环境下受经济调度或交易合约的影响；5）电网安全约束造成的出力限制，如电能输送路径在预想故障下出现的输送能力下降。一般使用“窝电”指称由电厂外部的限制因素（第4、5类）所造成的机组容量减扣现象，有时也作为具体问题研究中所关注的各类减扣的统称。

此外，还存在对机组出力下限的限制，如上述第4类因素也可能需要机组至少承担一定的出力，火力发电机组为确保锅炉等系统的正常运转而需维持的最低技术出力，等等。在进行机组出力优化时，有必要计入此类下限约束。

本文所提出的机组出力优化模型涉及由第3、5类因素产生的容量减扣和火电机组的最低技术出力。

2 计及输电通道容量约束的机组出力优化

本文首先针对运行方式确定的场景构建机组出力优化模型。

2.1 目标函数

考查某省级电网的拓扑结构，其简化接线图如图1所示），图中虚线框表示地理上的两个地区，实线框表示供电区域，各区域内部联系紧密，而各区域间仅通过少数通道（图中的实线）连接。该电网的主要特征为：东部地区仅包括YD区域，为主要的受电区域；西部地区包括YB、ZY、ZC、YX、JZ这5个区域，省外送入通道、多数机组和多数直流落点都位于此区域，潮流呈现明显的西部向东部输送。因此需确保图示3条关键通道（标示为①、②、③）向东部地区的传输功率尽可能大。

图1 某省级电网简化接线图Fig.1 Brief connection diagram of a provincial power grid

据此，本文以电网若干关键输电通道的正向传输功率最大和机组出力调整量最小为目标。

式中：f为优化目标；i、j为节点编号；Lij为支路i-j；ST为关键输电通道集合；Pij为支路i-j的正向传输功率；wT＜0为关键输电通道正向传输功率变量的权重系数；SG为可调机组集合；P0g为机组g的初始有功出力；Pg为机组g优化后的有功出力；wG＞0表示机组出力调节代价。

2.2 约束条件

1）潮流平衡约束

直流法潮流平衡仅考虑有功功率，并对参数作了简化，可使优化模型更简单、易求解。但存在优化后电网模型潮流不收敛的情况，因此一般仍采用交流法潮流平衡方程，将无功功率纳入优化模型。

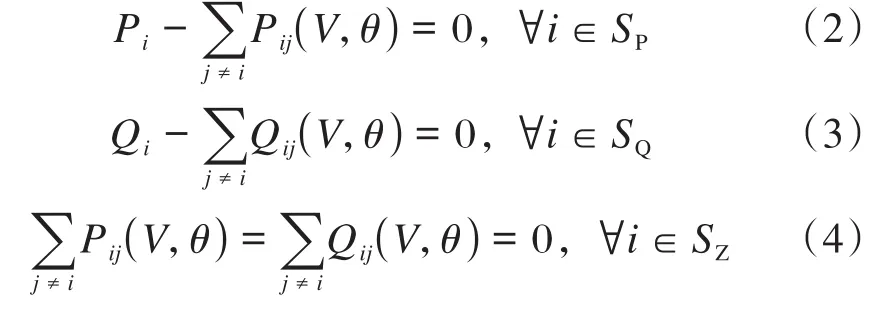
式中：Pi、Qi分别为节点i发出的有功功率和无功功率；Pij、Qij分别为以节点i-j间电压值V和相位差θ表示的支路有功功率和无功功率；SP、SQ分别表示发出（或消耗）有功功率、无功功率的节点集合；SZ为零注入节点集合。

为避免电网运行在可行域边界附近导致潮流极易不收敛，考虑对非PV节点添加电压限值。

式中：SV为PV节点集合；分别为节点i电压值Vi的下限和上限。

2）机组出力约束

这里添加的机组出力约束指因电厂固有电量消耗、机组最低技术出力等直接制约因素产生的对送出功率的限制，具体数据可直接收集、统计获得。

3）支路基态潮流约束

当两个节点间仅通过一条线路或变压器连接时，该线路或变压器的基态潮流以其载流能力的上限为约束。对于并列运行的多条线路或多台变压器，由于有功潮流的分配由设备参数决定，各设备流过的有功潮流与其参数近似线性相关，所以应把并列设备作为一个设备组［25］，统一添加运行约束。

式中：SD为设备组集合；分别为设备组D基态正方向功率（长期允许载流量）P0D的下限和上限（上标0表示基态），可通过各设备间的潮流比例和关键设备的长期允许载流量获得。对于无并列运行设备的情况，可视作仅有单个设备的设备组。

可考虑从设备组中选出潮流最容易越限的支路作为“监视支路”［26］，仅添加监视支路的潮流约束。记设备d的潮流占设备组D总潮流的比例为分支系数Kd，则监视支路为满足式（9）的支路。

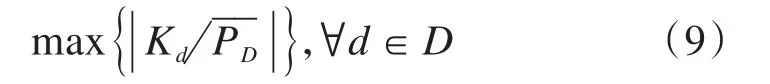
实际电网模型中可能存在无法消除的基态潮流越限，因此需对P0D作松弛，并在目标函数中添加参数，如式（10）所示。

式中：k0D为针对支路基态潮流值P0D添加的松弛变量；w0P为支路基态潮流变量的松弛代价。

4）预想故障潮流约束

除了基态潮流中所体现的输电通道容量限制，还需计入电网所关注各类故障下的潮流中所体现的通道限制，一般选择线路N-1和并列线路N-2下的安全约束。支路在故障下的潮流是其基态潮流及所开断各支路潮流的线性函数，因此，预想故障k发生后设备组D1的潮流约束为：

同样地，可仅添加监视支路的预想故障潮流约束，此时监视支路为满足式（12）的支路。

实际的电网模型中可能存在未消除或无法消除的预想故障潮流越限，优化后电网模型也很可能存在若干此类越限，因此需对PkD作松弛，并在目标函数中添加

式中：SkS为待考查预想故障潮流约束的设备组集合；kkD为针对PkD添加的松弛变量；wkP为预想故障潮流变量的松弛代价；D为集合的元素，即设备组。

5）区域间出力均衡约束

考虑各区域发电比例的均衡，定义区域n的机组出力水平为

式中：SA为电网中所划分区域的集合；Ga为区域a中的机组集合；Pg为机组g的出力；PEg为机组g的装机容量。

向模型中添加对各区域机组出力水平不均衡度的约束，如式（15）所示。

式中：TΣ为电网整体的机组出力水平；α%为允许的不均衡度上限。需注意，α%较小时容易导致优化问题无解，应当结合电网的运行经验确定该上限值。

2.3 对纯负荷断面的处理

电网中可能存在一类特殊的区域，其中不含任何电厂，仅有靠近负荷侧的变电站，整个区域完全依赖外界的电力输入，可称之为“纯负荷断面”。纯负荷断面的运行方式变化不会对机组出力产生影响，或称其对各机组出力的灵敏度为零。从另一角度来看，若纯负荷断面本身即存在（基态或预想故障下的）潮流越限，则无法通过调整机组出力的方法消除，这会导致机组出力优化问题无解。因此，有必要识别出这类区域并忽略其中的越限，或通过对变量和约束的松弛消除其对问题求解的影响。

3 基于检修计划的中长期发电计划联合优化

在形成针对特定运行方式的机组出力优化模型后，继续探讨基于检修计划获取中长期发电计划的联合优化方法。比如，针对月度检修计划形成相应的月度发电计划，之后可以该方案为基础，在日前再根据短期负荷预测等信息完成精细化的发电调度方案［27］。

以月度检修计划为例，所安排的检修时间粒度为一天，则每一天存在一个因设备检修安排而产生的运行方式断面。又由于实际上存在连续多天设备检修状态相同的情况，因此一个月内有区别的运行方式断面数并不多。合并相邻日期相同运行方式断面的过程如图2所示。

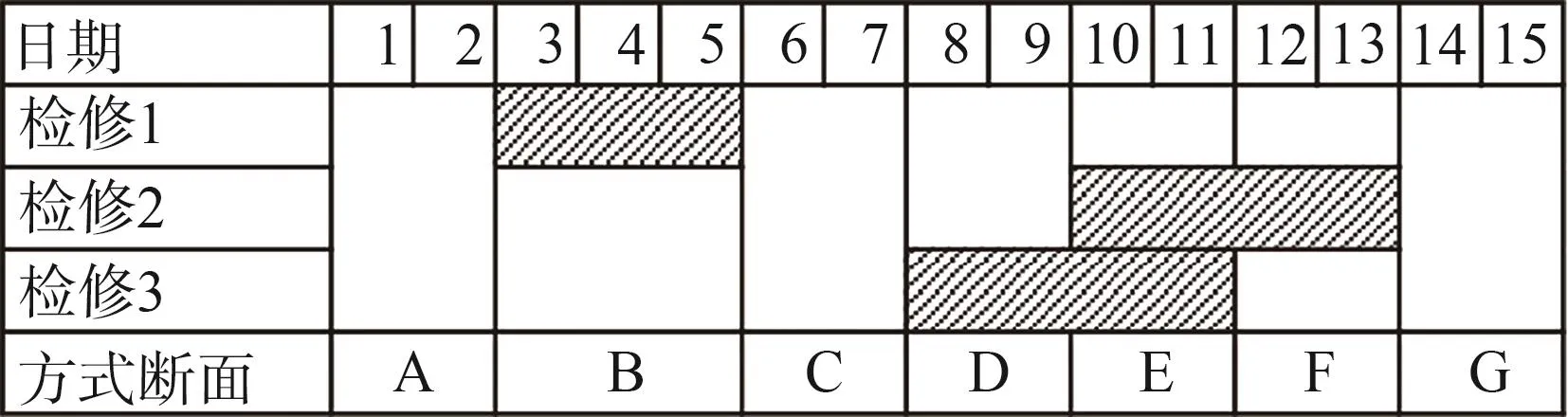
图2 运行方式断面示例Fig.2 An example of creating the operation mode snapshots

为根据检修计划形成相应的发电计划，可依次对每个运行方式断面应用机组出力优化，并将出力调整结果作为后一个方式断面的基础，如此不断完成针对各方式断面的优化。

基于检修计划的中长期发电计划联合优化流程图如图3所示。

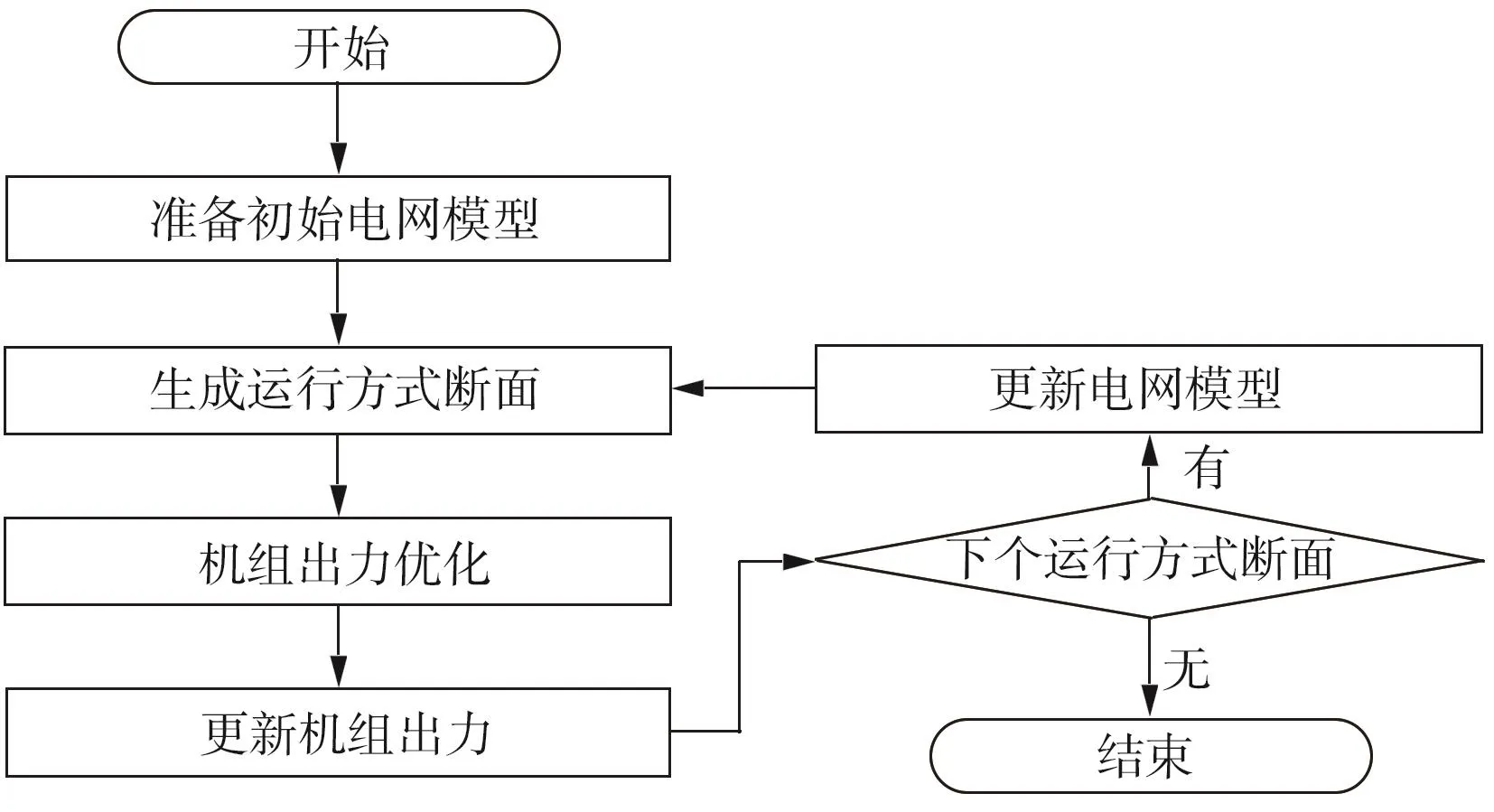
图3 基于检修计划的中长期发电计划联合优化流程图Fig.3 Flow chart of combined optimization of medium- and long-term generation scheduling based on maintenance plans

4 算例分析

本文采用某省级电网的数据进行测试和分析。该电网的简化接线图如图1所示，其中共有统调机组299台，包含若干不可调机组和窝电程度偏高的机组。所考查的预想故障包括500 kV和220 kV等级的线路N-1和并列线路N-2。

4.1 确定运行方式下的机组出力优化结果

4.1.1 优化模型求解

使用某个运行方式下的PSD-BPA模型，该方式已由运行人员调整机组出力以提升东部地区受电量并改善窝电情况。其中有2 531项预想故障待考查，所生成的机组出力优化模型含有93 748个变量，78 594条等式约束，51 257条不等式约束。

基于以下考虑确定模型中的各系数：“关键输电通道正向传输功率最大”是本研究所关注的关键目标，而“机组出力调整量最小”是各类涉及机组出力调整的优化方法中的通用目标之一，因此有|wT|＞wG以优先满足关键目标；优化目标应在各潮流约束尽量不越限的情况下达成，因此松弛代价系数应大于上述两系数；又由于需优先满足基态潮流约束，则有w0P＞wkP。本算例使用的系数见表1。

表1 机组出力优化模型中的系数Tab.1 Values of the coefficients in the optimization model

对于所生成的模型采用原对偶内点法优化，采用不对称分解法求解修正方程，在迭代39次后收敛，求解过程中的不可行性变化曲线如图4所示。可以看出，本文所提出的机组出力优化模型可快速、有效地获得最优解。

图4 机组出力优化求解过程中的不可行性变化曲线Fig.4 Infeasibility curves during the iteration of the generation optimization

4.1.2 关键输电通道正向潮流变化情况分析

优化后关键输电通道正向潮流的变化情况如图5所示。

图5 关键输电通道正向潮流变化情况Fig.5 Power flow changes of key transmission channels

相较于优化前的运行方式，东部地区通过3条关键输电通道获得的电量有所上升。但通道③传输功率下降，是因为初始运行方式下该通道在东部地区的落点附近存在多项预想故障下的潮流越限，且难以消除。

4.1.3 潮流越限情况分析

该运行方式在优化前后均无基态下的潮流越限，以下比较预想故障下的潮流越限情况：优化前的电网模型中不含线路的基态潮流越限，在72项预想故障下的线路潮流越限中，有18项越限位于500 kV通道，其中8项涉及关键输电通道；优化调整后的电网模型中不含线路的基态潮流越限，在47项预想故障下的线路潮流越限中，有5项越限位于500 kV通道，其中1项涉及关键输电通道，3项位于通道③在东部地区的落点附近。优化前后500 kV通道潮流越限情况如表2所示，各项越限在优化后得以消除或越限率明显降低。

表2 优化前后500 kV通道的潮流越限情况Tab.2 Power overflow changes of 500 kV transmission channels

4.1.4 机组出力调整情况分析

优化过程对各电厂出力的调整情况如图6所示，该柱状图中的每个条柱表示一个电厂的出力调整量。

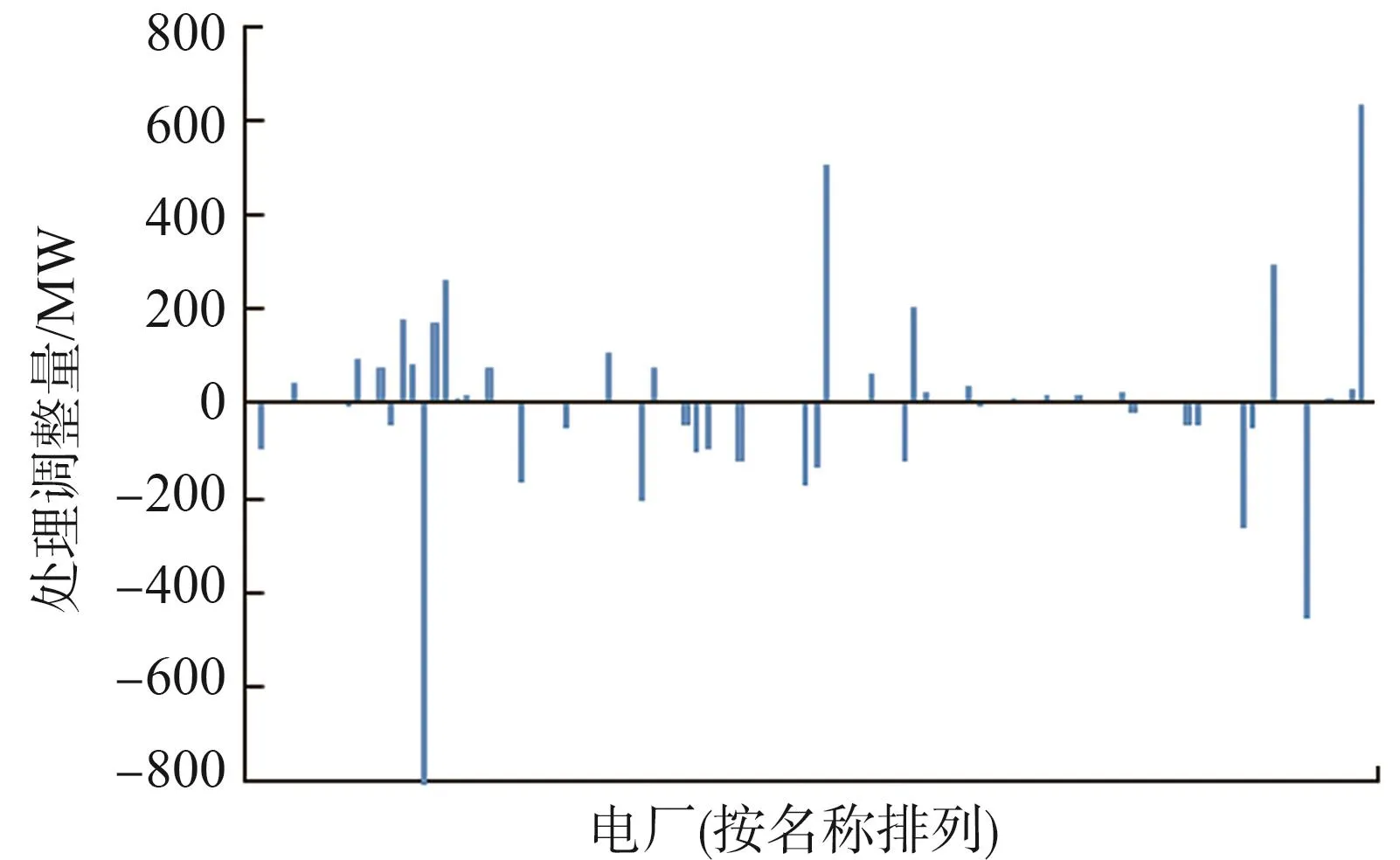
图6 优化过程对各电厂出力的调整情况Fig.6 Generator output adjustments during the optimization

由于机组出力调节代价系数小于其他系数，所以会出现为消除潮流越限或关键输电通道传输功率而大幅调节机组出力的情况。以下选取几种典型情况对此做出说明。

优化后出力增加的电厂多位于西部地区，这与关键输电通道正向传输功率最大的目标相符。较特殊的是，出力上升最多的电厂位于东部地区，这主要用于应对通道③传输功率下降导致的用电缺口。

在受窝电影响而做出调整的电厂中，出力下降最多的是HM厂，相关电气连接如图7所示。其通过并列的3条500 kV线路连接到LG站，在并列线路N-2时仅通过一回线路向外供电，则HM厂出力受到其中载流能力最小的HM-LG（Ⅲ）线的制约。

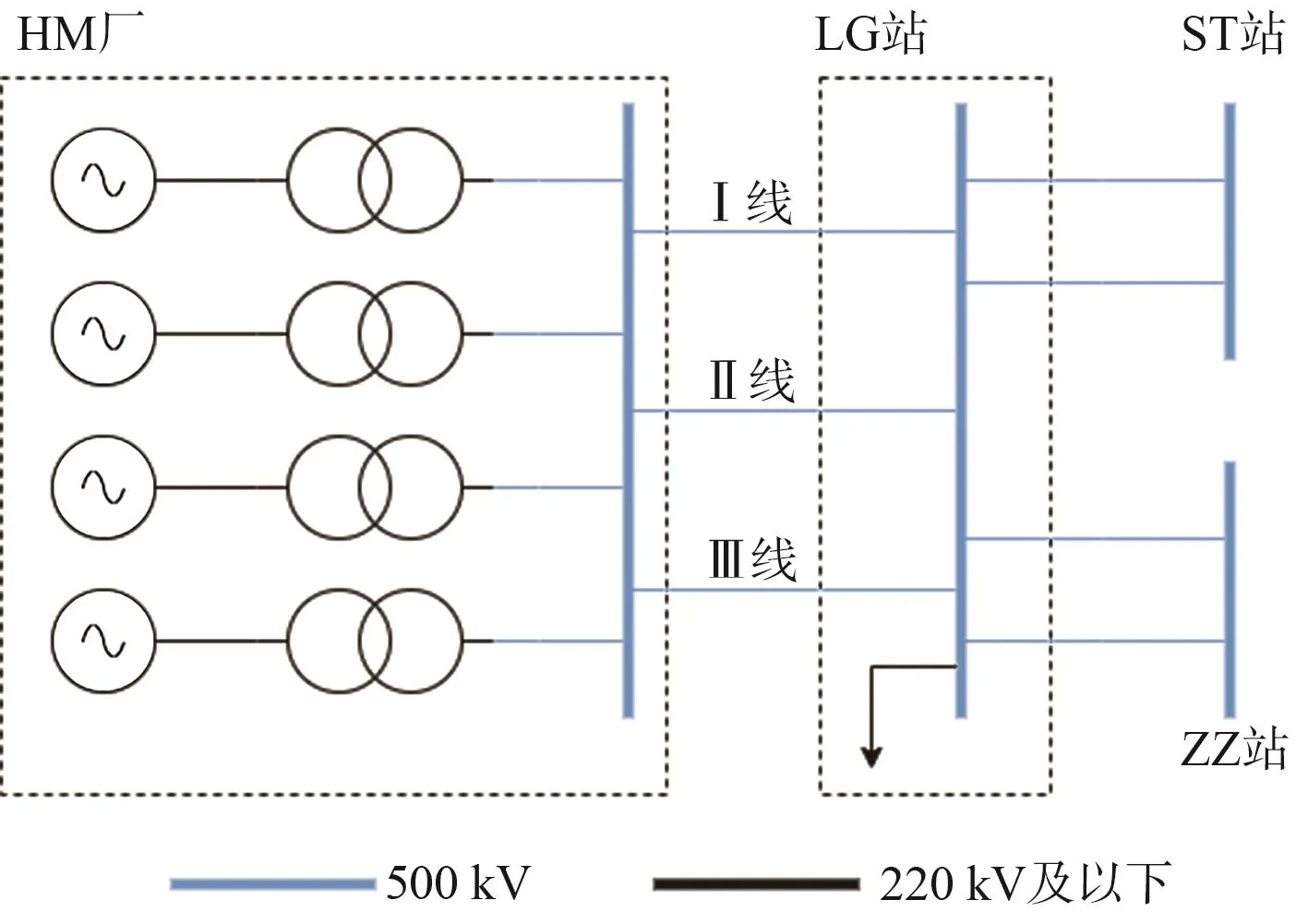
图7 HM电厂电气连接示意图Fig.7 Electrical diagram of “HM” power plant

再以另一个局部区域为例，厂站连接情况如图8所示。

图8中有4个电厂，通过GA、JL两个500 kV变电站向外供电。在初始运行方式下，ZA-BY-JHBT-JL路径存在若干预想故障下的潮流越限情况。优化过程对各电厂出力的调整如表3所示，通过限制ZA厂和BH厂的出力消除了各项越限。

表3 电网局部区域电厂出力调整情况Tab.3 Power plant output adjustments in the subarea of the grid

图8 电网局部区域厂站连接情况Fig.8 Connections of the substations in a subarea of the grid

4.1.5 小结

该算例表明，本文提出的优化模型可快速获得最优解；给出的机组出力调整方案消除或减轻了大量潮流越限情况，电网各局部区域以及各地区间的潮流分布更合理，关键输电通道正向传输情况符合预期，明显优于运行人员通过经验和大量计算确定的运行方式。

针对部分机组出力调整量较大的情况，可考虑对不同机组设定不同的调节代价。但这会导致目标函数中不同系数间的配合更改困难，一组固定系数的适用范围变窄。此问题有待进一步研究。

4.2 基于检修计划的月度发电计划优化结果

使用某月的部分检修计划及相应运行方式下的PSD-BPA模型进行测试，其中包括6项检修计划，共产生6个运行方式断面，如图9所示。

图9 按检修计划产生的运行方式断面Fig.9 Operation mode snapshots created according to the maintenance plan

针对各运行方式断面使用各自的基态模型分别优化和使用本文提出的发电计划联合优化流程，所得机组出力总调整情况的对比如图10所示。

图10 针对各运行方式断面的机组出力总调整量对比Fig.10 Comparison of generator output adjustmentsupon the operation mode snapshots

可以看出，使用分别优化时各方式断面的机组出力调整量维持在较高水平，使用联合优化方法时出力调整量明显减少。特别地，两种优化方法针对方式断面A的出力调整量相同，是因为两者基于相同的基态模型进行优化。

5 结论

本文针对输电通道容量限制导致的机组窝电情况进行讨论，并将相关约束条件引入确定运行方式下的发电优化模型中，以关键断面传输效率最大和机组出力调整量最小为目标获得相应的最优发电计划。又针对检修计划扩展了所述发电优化模型，获得与之相适应的中长期发电调度基础方案。使用某省级电网的模型数据和检修信息对所述方法进行了验证，得出结论如下。

1）所采用的发电优化模型消除了各设备组中的冗余约束，可在缩减模型规模的同时不对优化结果的精度产生影响；

2）优化模型给出的机组出力调整方案可有效消除或减轻电网中的潮流越限情况，合理分配潮流并确保关键输电通道的传输效率；

3）所提出的发电计划联合优化方法通过合并相同运行方式断面以减少计算量，基于前一个断面优化结果的联合优化策略可大幅降低各运行方式下的机组出力调整量。

后续研究将考虑在发电计划中计入更多运行约束，进一步提升方法的实用性。