基于离散元模拟的黏土劈裂注浆扩散特性
2022-02-02张泽甫成远登丁文云张永明念培红刘海明
张泽甫,成远登,丁文云,陈 培,张永明,念培红,刘海明
(1.云南省滇中引水工程建设管理局,昆明 650051; 2.昆明理工大学 建筑工程学院,昆明 650500; 3.中铁二院昆明勘察设计研究院有限责任公司,昆明 650500; 4.保(山)施(甸)高速公路投资开发责任公司,云南 保山 678200)
1 研究背景
滇中引水工程伍庄村隧洞穿越“滇中红层”,软岩洞段存在极严重变形风险,施工难度极大,其洞口存在大量的黏土。黏土具有强度低、压缩性高等不良性质,在工程中对软弱黏土处理不当,极易发生边坡失稳、突水突泥等灾害性事故[1-5]。劈裂注浆作为加固软弱黏土最有效的手段之一,其施工工艺较为成熟。但注浆过程隐蔽且相关物理模型试验重复性差,目前主要通过数值模拟对劈裂注浆展开研究,具有可视化程度高、经济、合理等显著优势[6-8]。
黏土注浆后宏观表现与其细观特性存在必然的联系[9]。因此,大量学者们从细观角度研究注浆加固软弱土体的效果。孙峰等[10]基于颗粒流分析方法,运用PFC2D内置的Fish语言探讨了致密土体在不同注浆压力及土体性质对劈裂注浆裂缝的发生和扩展规律;耿萍等[11]通过离散元软件PFC2D发现浆液扩散形式主要受控于注浆压力,验证了劈裂注浆是压密-劈裂-压密-劈裂的动态过程;秦鹏飞[12]运用PFC2D内置Fish tank函数库和Fish语言对浆液扩散过程、形态和颗粒的位移情况进行了数值模拟,提出浆液黏度的增加可以提高劈裂-压密注浆效果;夏洋洋等[13]借助二维颗粒流程序PFC2D建立了高聚物定向劈裂注浆的可视化模型,研究了浆脉扩散形态、浆液颗粒数量及土体弹性模量对浆液扩散和土体孔隙率的影响规律。
为了从细观角度研究劈裂注浆对伍庄村隧洞进口段软弱黏土加固效果,本文基于流固耦合理论和平板窄缝流动模型,通过离散元软件PFC2D内置Fish语言的二次开发,实现黏土在劈裂注浆过程中浆液与土体颗粒之间的耦合。进一步研究注浆压力、颗粒粒径比及黏结强度对浆液扩散特性和土体孔隙率的影响规律,并通过室内试验验证其数值结果的正确性,为洞口段注浆加固工程提供参考。
2 离散元流固耦合原理
PFC2D中将黏土视为离散颗粒的集合体,通过颗粒介质的运动及相互作用来模拟注浆过程中颗粒材料的力学特性。模型中并没有实际流体存在,而采用“流体域”和“流体通道”的连接实现颗粒与流体的耦合。“流体域”是指储存浆液的“域”,周围管道的尺寸会影响“流体域”体积,随着计算时步的进行,“流体域”中的流体压力也会进行计算,并将流体压力作用至附近的颗粒。“流体通道”是指供浆液流动的管道,存在于颗粒接触之间,管道通过连接形成流体网络。并通过细观分析颗粒的受力,若颗粒之间产生裂纹则反映了土体浆液的扩展与贯通。
颗粒流程序中“流体域”与颗粒间的耦合作用方式分为3种:①通过颗粒间接触的张开、闭合或接触力的变化使通道直径发生变化;②研究“域”的力学特性的变化引起“域”压力的改变;③“域”体积压力变化对其周围颗粒的推移作用。因为第一种方式简单易实现,本文采用第一种方式实现流固耦合,并借助PFC2D内置Fish语言定义流动方程和压力方程。
2.1 流体方程
本文将土体孔隙的几何形状看作一系列圆形质点的集合,其相邻区域间有一个“流体通道”。流体储存于“流体域”中,在压力差作用下,流体流动到其他“域”。假设颗粒间的流体通道为平板窄缝流动模型如图1所示,垂直于x-y平面,单位宽度b的平板通道长度为L,开度为a。若浆液在流体通道流速较小,即为单向层流状态。根据流体缝隙流动的立方定理,通过孔隙间的流量q为
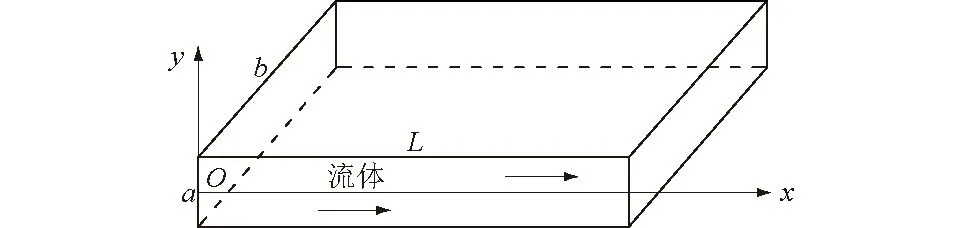
图1 浆液流动平板窄缝流动模型Fig.1 Plate narrow slit model for slurry flow
(1)
式中:k为渗透系数;Δp为孔隙间压力差。
2.2 压力方程
为实现流体与颗粒在注浆过程中动态耦合作用,储存在流体域内的流体压力在不断更新。在单位时间步内流体流动会导致其压力变化,可由流体体积模量计算。假设单位时间步为Δt,流体增量为∑q,则通道内流体压力的计算公式为
(2)
式中:Kf为流体的体积模量;Vd为孔隙体积。
2.3 流体计算时间步长
计算采用显式方法求解,分别将流量方程应用于所有平板窄缝流动模型,将压力方程应用于所有“流体域”,在所有“流体域”内交替应用流动方程和压力方程。为保证模型运行稳定,流体引起的压力变化必须小于扰动压力。当两者相等时可求出临界时间步长Δt为
(3)
式中:r为流体域周围颗粒的平均半径;N为流体域所连接的管道数。
3 建立数值模型
3.1 土体颗粒模型建立
颗粒流方法中不存在实际材料的本构模型,通过定义颗粒的接触本构模型和设置细观力学参数反映其力学性质。由于黏性土黏粒含量较多,由大量具有带电性的黏性矿物组成,呈絮状结构,具有一定的黏结力。因此,本文选用颗粒接触黏结模型来模拟黏土颗粒间的接触。土体颗粒形状由圆球替代,模型的长×宽为80 cm×80 cm。模型由颗粒单元和流体单元组成,颗粒单元一部分为注浆土体,另一部分为不透水边界。将边界上的颗粒速度和位移设置为零,既可防止模型内部颗粒逸出,也有利于保持模型内部应力稳定。
假设数值模型面积为S,颗粒孔隙率为n,最大、最小颗粒半径分别为Rmax和Rmin,颗粒平均半径用r表示,按照式(4)即可计算出模型区域内生成的颗粒数目。
(4)
颗粒流计算模型中细观参数的合理选择是计算准确的关键。颗粒流程序中不能直接输入土体的宏观力学参数,因此通过试错法对细观参数进行试算,并参考国内外相关文献,确定数值模拟试验的细观参数,取值见表1。

表1 黏土颗粒细观力学参数Table 1 Mesoscopic mechanical parameters of clay particles
3.2 “流体域”和“流体通道”的生成
流体单元一部分为“流体域”,另一部分为“流体通道”。本文基于Fish语言的编写定义流动方程和压力方程,生成的“流体域”和“流体通道”如图2所示,其中红色的点代表“流体域”,“域”间绿色线段代表“流体通道”。本文流体采用的细观计算参数见表2。其中,流体计算时间步长按照式(3)计算,水头压力等其他参数根据达西渗透试验获得[14]。
图2 “流体域”和“流体通道”示意图Fig.2 Sketch of fluid domain and fluid channel

表2 流体域基本参数Table 2 Basic parameters of fluid domain
3.3 建立流固耦合模型
按照式(4)计算生成颗粒数量,运行5 000时步时生成颗粒数量3 632个,颗粒粒径在3.5~5.0 mm均匀分布。通过调用Fishtank中的zap-dead-ends删除“悬浮颗粒”(即颗粒接触≤1的颗粒)1 769个,确保所有“流体域”都完整有效。最终建立颗粒与流体之间的耦合过程如图3所示。
图3 颗粒单元与流体单元耦合示意图Fig.3 Schematic diagram of the coupling between particle unit and fluid unit
由于PFC2D不能直接获取孔隙率等信息,为记录颗粒模型的相应信息,本文设置了3个监测圆进行记录。通过自定义Fish语言,最终导出监测圆区域内的相关信息。监测圆的圆心为模型中心,半径尺寸依次设置为10、20、30 cm,建立的模型如图4所示。模型中心为注浆孔,白色的圆代表土体颗粒,绿色的圆代表不透水边界,蓝色区域代表监测圆。

图4 土体颗粒模型和监测圆Fig.4 Soil particle model and measurement circles
4 数值模拟分析
注浆后浆液在土体中的扩散半径可反映浆液与土体接触胶结的充分程度,并且浆脉网络的骨架作用对注浆加固土层的影响显著。此外,土体孔隙率也是影响多孔介质内流体传输性能的重要参数,反映了土体的致密程度,对土体结构有重要影响。因此,本文通过注浆后浆液扩散半径和土层孔隙率的变化研究浆液在黏土中的扩散规律,具体数值模拟试验方案如表3所示。

表3 数值模拟方案Table 3 Numerical simulation schemes
4.1 注浆时间对浆液扩散特性的影响
注浆时步与浆液扩散半径关系如图5所示,在土体颗粒细观力学参数和流体基本参数取值相同的条件下,选取注浆压力为0.5 MPa,随着注浆时步的增加,裂缝数量增多,浆液扩散半径不断增大,说明注浆时步对浆液扩散半径有明显影响。当注浆时步增加到1 000时,继续增加注浆时间,浆液扩散半径增速放缓,符合实际情况。

图5 注浆时步与浆液扩散半径关系Fig.5 Relationship between grouting step and slurry diffusion radius
4.2 注浆压力对浆液扩散特性的影响
注浆压力与浆液扩散半径和孔隙率的关系如图6所示。由图6(a)可以看出,注浆压力在0.50~1.25 MPa时对浆液扩散半径影响较为明显,随注浆压力的增加,扩散半径变化曲线变缓。当注浆压力为0.5 MPa时,未达到土体启劈压力,土体中不产生浆液扩散。当注浆压力增大时,浆液开始劈裂土体产生劈裂缝,浆液扩散半径也随之增加。数值模拟结果表明,当注浆压力达到1.5 MPa时扩散半径最大,为30.1 cm。
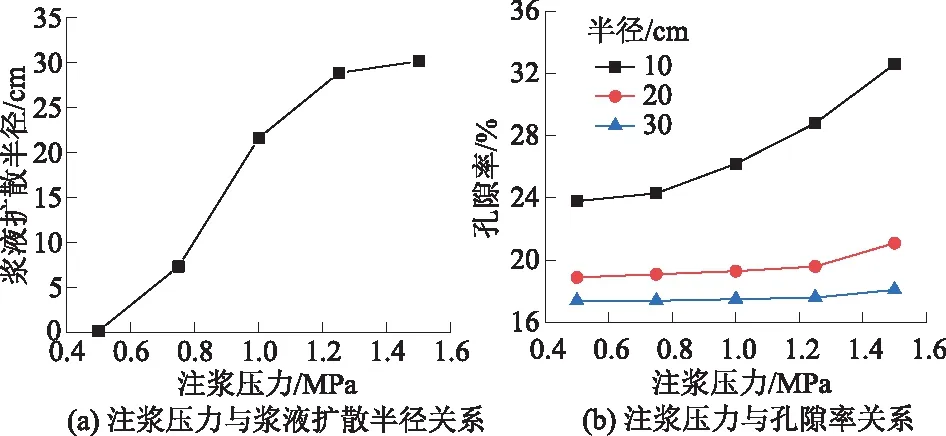
图6 注浆压力与浆液扩散半径和孔隙率关系Fig.6 Relations of grouting pressure against slurry diffusion radius and porosity
监测圆半径10、20、30 cm范围内,注浆压力作用下土体孔隙率的变化趋势线见图6(b),从图中可明显看出注浆压力对10 cm范围内土体的孔隙率影响较大。注浆压力为0.5 MPa时,最大孔隙率为23.8%;压力增加到1.5 MPa时对应孔隙率增加至32.8%,孔隙率相对增加了37.8%。并且距离中心注浆区越近的土体,孔隙率增加幅度越大。
可以发现,当注浆压力大小合适时,土体注浆加固效果明显,劈裂缝分布较好,生成稳定的浆脉网络,可有效改善土体性质。若注浆压力过高,浆液最大扩散半径范围虽有提高,但土体中产生的劈裂缝分布混乱,会导致土体间的小裂隙连接贯通形成大裂隙,导致土体稳定性降低,容易发生土体冒浆等现象,导致实际施工难度增大。若注浆压力过低,则浆液扩散半径范围有限,生成的劈裂缝少,难以形成浆脉网络,导致土体加固效果不理想。
4.3 颗粒粒径对浆液扩散特性的影响
为讨论土体颗粒粒径比(Rmax/Rmin)对黏土中劈裂注浆扩散特性的影响,本文控制注浆压力和注浆时间不变,采用不同土体颗粒粒径比得到浆液扩散半径和土体孔隙率变化规律,如图7所示。

图7 颗粒粒径比与浆液扩散半径和孔隙率关系Fig.7 Relations of particle size ratio against slurry diffusion radius and porosity
从图7(a)明显看出,随着土体颗粒粒径比的增大,浆液扩散半径降低,注浆对土体的影响范围明显缩小。这是因为增大土体颗粒粒径比,土体级配更好,较大的土体颗粒之间越容易产生孔隙,较小的土体颗粒会填充在孔隙里,使颗粒之间接触更加紧密,土体模型越发密实,浆液扩散范围随之减少。颗粒粒径比为2.7时浆液扩散半径最大,为17.6 cm,增至2.9时扩散半径下降幅度为32%,当粒径比增加到3.3时扩散半径仅有7.1 cm。由此说明劈裂注浆中浆液扩散范围受到粒径比的影响较大。
此外,在距离注浆孔10 cm范围内,当颗粒粒径比超过2.9时,土体孔隙率下降幅度最大。并随粒径比的增大土体初始孔隙率降低,土体产生劈裂注浆所需能量更高。注浆压力作用下注浆孔周围土体对外围土体有压密作用,导致在距离注浆孔越远的土体孔隙率越低。
4.4 颗粒黏结强度对扩散特性的影响
法向、切向黏结强度对扩散特性的影响分别如图8、图9所示。由图8(a)、9(a)可知,颗粒法向和切向黏结强度对浆液扩散半径呈递减趋势。随黏结强度的增加,劈裂缝生成的数量递减,对土体的影响范围减小。当法向黏结强度超过0.7 MPa时,土体的劈裂缝大幅下降,浆液扩散半径≤5 cm。而切向黏结强度达到1.0 MPa时对土体扩散半径影响较大。故可明显看出,颗粒间法向黏结强度相比于切向黏结强度对浆液扩散半径影响更大。
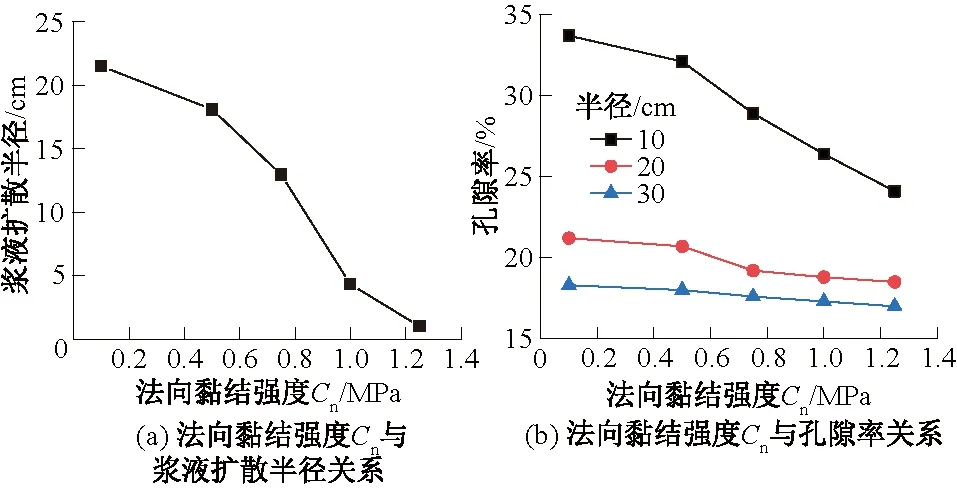
图8 法向黏结强度Cn与浆液扩散半径和孔隙率关系Fig.8 Relations of normal bonding strength Cn against slurry diffusion radius and porosity
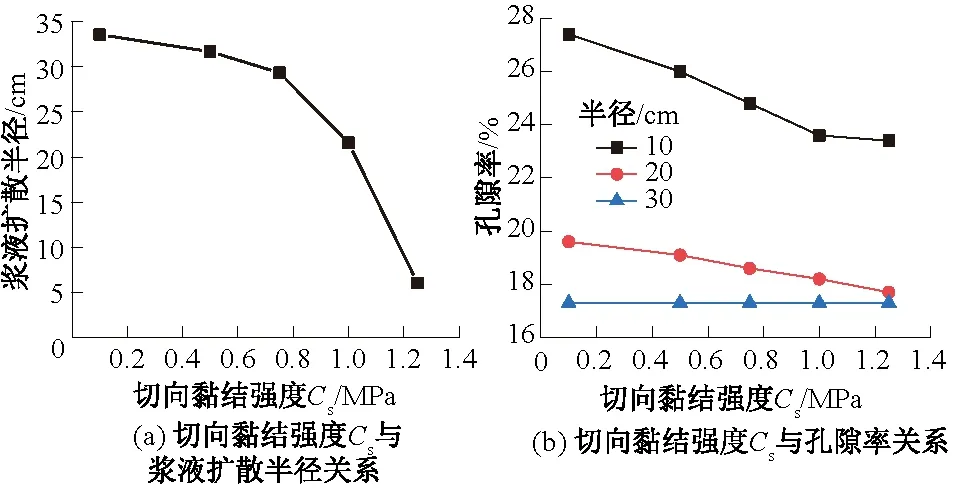
图9 切向黏结强度Cs与浆液扩散半径和孔隙率关系Fig.9 Relations of tangential bonding strength Cs with slurry diffusion radius and porosity
随着颗粒黏结强度的增加,颗粒之间接触力变强,在注浆压力作用下很难出现位移,造成土体孔隙率的减小。由图8(b)、9(b)可以看出,黏结强度的增加对土体一定范围内孔隙率有不同程度的影响。10 cm范围以内影响最为显著,随着离注浆孔的距离越远,对孔隙率影响越低。切向黏结强度对30 cm范围外土体的孔隙率影响甚小。
随着法向、切向黏结强度的增大,浆液扩散半径减少,距离注浆孔不同范围土体孔隙率有不同程度的降低。这是由于在PFC2D中,颗粒间接触强度由黏结强度决定。提高土体颗粒黏结强度,土体颗粒的黏聚力也会随之提高,颗粒间胶结作用会增强,因此破坏颗粒间的接触需要更大注浆压力才能生成劈裂缝。
5 室内注浆试验对比
5.1 室内试验
试验用土选用云南省楚雄市某地红黏土,主要由白云岩、泥质岩等经风化作用后形成,黏土呈红褐色。根据《土工试验方法标准》(GB/T 50123—2019)[15],对红黏土宏观力学参数开展相关土工试验,得到红黏土的基本特性见表4。模型试验浆液的水灰比为0.7,注浆压力设定为0.5、0.6、0.7 MPa,得到试验土体中的水泥浆脉形态及分布见图10。

表4 红黏土基本参数Table 4 Basic parameters of red clay

图10 不同注浆压力下的浆脉形态及分布Fig.10 Formation and distribution of slurry veins under different grouting pressures
在3种注浆压力下,黏土地层水平方向生成一条主浆脉和一条次浆脉呈直线延伸。注浆压力为0.5 MPa时浆液扩散半径19.4 cm;0.6 MPa时扩散半径28.7 cm;0.7 MPa时扩散半径35.6 cm。由量测数据可知,浆液扩散半径与注浆压力呈正相关关系。
5.2 对比分析
针对室内劈裂注浆模型试验建立数值模型,并根据室内三轴试验进行参数标定[16],结合土体颗粒宏细观参数间的关系进行取值[17],参数取值见表5。

表5 红黏土颗粒基本细观力学参数Table 5 Mesoscopic mechanical parameters of red clay particles
室内试验采用普通硅酸盐水泥浆液,属于典型的宾汉姆流体,水泥浆液的黏度和密度与水有较大区别。因此,先以水作为渗流流体得到的渗透系数进行换算,得到特定水灰比下水泥浆液的渗透系数,换算渗透系数的计算公式[18]为
(5)
式中:kg表示以浆液作为渗流流体的渗透系数;ko表示以水作为渗流流体的渗透系数;ηw表示水动力黏滞系数;ηg表示浆液动力黏滞系数;ρg表示浆液密度;ρw表示水的密度;β表示浆液与水的黏度比。将具体数值代入得到浆液的渗透系数为5.17×10-8m/s。
通过数值模拟计算得到不同注浆压力下最终浆液扩散半径,见图11,图中红色裂缝代表浆液扩散半径的范围。提取模拟数据可知,当注浆压力为0.5 MPa时,最大扩散半径22.3 cm;0.6 MPa时最大扩散半径31.2 cm;0.7 MPa时最大扩散半径为37.5 cm。

图11 不同注浆压力条件下浆液最终扩散范围Fig.11 Range of final diffusion of slurry under different grouting pressures
将数值模拟试验结果的浆液扩散半径与室内注浆试验结果进行对比分析,发现二者曲线趋势吻合较好,曲线间的数值相差较小,见图12。结果表明,劈裂注浆数值模拟和室内劈裂注浆试验的结果与注浆压力均呈正相关关系。浆液扩散半径随注浆压力的增大而增大,与工程实际相符,验证了本文建立的注浆数值模型的正确性。
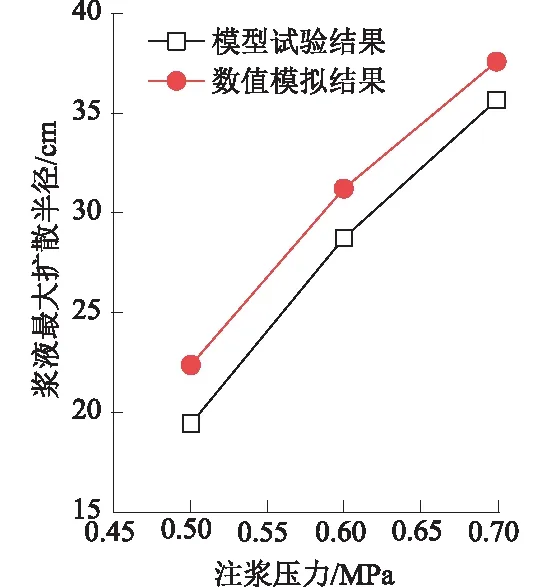
图12 数值模拟结果与室内 试验结果对比Fig.12 Comparison of slurry diffusion radius between numerical simulation and indoor test
5.3 误差分析
PFC2D数值模拟试验结果与室内注浆试验结果趋势上吻合较好,但数值上存在一定的偏差,分析原因如下:
(1)浆液在土层中的扩散规律的影响因素多元且复杂。模拟中忽略了浆液黏度时变性、浆液在土体扩散过程中的压力损失等因素,导致理论结果和实际结果有偏差。
(2)本文假定流体流动满足平板窄缝流动模型,并符合达西定律。但实际土体劈裂注浆产生的裂缝分布混乱且不均匀,土体中浆液的扩散过程不完全符合平板窄缝流动模型。
(3)本文建立的黏土劈裂注浆数值模型为二维模型,然而实际土体劈裂注浆是一个三维过程。因此与实际情况存在一定差异。
6 结 论
(1)基于颗粒流程序有效模拟劈裂注浆过程中浆液与土体颗粒的耦合作用,实现了劈裂注浆裂缝的生成和发展可视化。数值模拟结果表明,注浆压力和注浆时间对浆液最大扩散半径呈先增加后减缓的趋势,孔隙率随距注浆孔距离越近,增大幅度越大,合理选择注浆压力和注浆时间可有效改善土体加固效果。
(2)颗粒粒径比Rmax/Rmin直接影响土体结构强弱,对浆液扩散半径和土体孔隙率的影响较大。粒径比越大,土体越密实,导致扩散半径逐渐减小,并且随距离注浆孔距离的增加,颗粒粒径比对土体孔隙率的影响逐渐减小。
(3)颗粒间黏结强度与浆液扩散半径呈反比。对于黏结强度较高的土体,为了达到劈裂注浆效果,需增大注浆压力。且法向黏结强度对浆液扩散半径和土体孔隙率的影响相对于切向黏结强度更大。
(4)对劈裂注浆进行室内试验,发现浆液扩散范围受注浆压力的影响较大。试验结果与数值模拟进行对比,发现二者曲线间误差较小,与工程实际相符合。针对伍庄村隧洞进口段应根据地质条件确定最佳注浆压力达到最优加固效果。
