同质网络中具有时滞的谣言传播模型的动力学分析∗

童新如，蒋海军,2†，陈向勇

(1.新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017；2.伊犁师范大学 数学与统计学院，新疆 伊宁 835000；3.临沂大学自动化与电气工程学院，山东 临沂 276005)

0 引言

谣言是指没有相应的事实依据而被捏造出来的一种言论.而网络又是自由交流的平台,于是越来越多的网络谣言出现在人们的生活里.在信息全球化时代,谣言不再受制于时间与空间,任意一条网络谣言都可能在全世界范围内实时大量的传播,从而扰乱正常的生活秩序,以至于带来一系列的负面影响[1−2].例如一些人在网上散布谣言称生活必需品的价格将大幅上涨,以至于一些市民抢购生活用品从而造成市场混乱.类似的事件层出不穷,这些事实都告诫我们:由于网络谣言越来越多且影响恶劣,因此研究网络谣言的传播机制进而控制谣言具有重要意义.

谣言传播与传染病传播有很多相似的地方.一直以来,谣言传播模型大多借鉴了传染病模型的成果.最为经典的谣言传播动力学可以追溯到1965年Daley和Kendall所提出的DK模型[3],以及Maki和Thompson所提出的MT模型[4].尽管DK模型和MT模型只适用于描述传统口口相传的小范围谣言传播过程,不能完全反映谣言传播的现实特征,也没有考虑到网络的拓扑结构对谣言传播的影响,但它们却为后来研究复杂网络上的谣言传播提供了研究框架和一定的理论基础.

近年来,国内外众多学者利用数学模型对谣言传播进行了定性描述,并且给出了谣言消除或盛行的阈值条件.此外,关于谣言传播的分析,学者们主要做了以下两方面研究:一方面,随着复杂网络理论的快速发展,越来越多的学者开始研究网络拓扑结构对谣言传播的影响[5−7].值得注意的是,Zanette首次将复杂网络理论引入到谣言传播模型中,并建立了小世界网络中的谣言传播模型[8−9].研究表明,网络结构对谣言的传播有显著的影响.此后,越来越多的学者将谣言传播的动态行为与网络的拓扑特征联系起来,进一步提出了基于不同网络结构的谣言传播模型来阐明谣言在不同环境下的传播过程[10−12].另一方面,为了进一步地了解谣言在现实世界中的传播动态,许多学者考虑了各种各样的谣言传播机制,如信任机制[13]、遗忘机制[14]、潜伏机制[15]、怀疑机制[16]等.不可否认,网络的拓扑结构和各种各样的传播机制在谣言的传播过程中发挥着重要作用.

值得指出的是,犹豫机制在谣言传播过程中也起着重要作用.最近,为了研究犹豫机制对谣言传播的影响,Liu等建立了具有犹豫机制的谣言传播模型[17]，并指出个体在面对谣言时一般具有犹豫的心理.然而,在真实的谣言传播过程中,人们面对谣言时往往不仅会犹豫,而且还会表现出不同的个体行为,即当谣言易感个体听到谣言后,往往有三种不同的行为选择:第一种选择是相信并传播谣言从而成为谣言传播个体;第二种选择是犹豫是否传播谣言从而成为谣言犹豫个体;第三种选择是对谣言不感兴趣从而成为谣言恢复个体.因此,本文将在同质网络中考虑这三种不同的个体行为对谣言传播的影响.

此外,由于谣言在传播的过程中会有复发的可能性,Yao等建立了具有复发机制的谣言传播模型[18].谣言的复发是指一些谣言传播个体可能在当下阶段由于某些原因而停止传播谣言,但在下一阶段可能会因为一些不可预见事情的发生又重新燃起了传播谣言的兴趣,从而选择再次传播谣言.显然,将复发机制考虑到谣言传播的过程中会更加接近谣言传播的真实情况.另一方面,注意到上述研究并没有考虑到网络拓扑结构以及复发时滞对谣言传播的影响,也没有对谣言传播平衡点的全局稳定性进行严格的理论分析.事实上,这些因素对谣言传播的建模分析来说是至关重要的.于是,本文将建立同质网络中具有谣言复发和复发时滞的谣言传播模型来更好地刻画谣言,并且对谣言传播平衡点的全局稳定性进行严格证明.除此之外,Allport和Postman认为,被讨论的信息如果内容越重要并且表达越模糊,那么谣言传播的速度越快,进而影响的范围和程度就越大[19−20].因此,本文将内容的重要性和模糊性统一看作谣言对个体的吸引性从而刻画个体对谣言的感兴趣程度,并且在建模过程中引入谣言吸引性参数m,从而建立了同质网络中具有时滞的SHILR谣言传播模型.

1 模型建立

本节将利用复杂网络理论对谣言传播过程进行建模.其中,节点表示所有使用社交网络平台的个体,而两个节点之间的连边则表示通过网络连接的两个体之间的联系.因此,谣言可以通过这些节点之间的边进行传播.假设网络的平均度是〈k〉,并且将网络中的用户分为五类,分别表示t时刻的谣言易感个体S(t),谣言犹豫个体H(t),谣言传播个体I(t),谣言潜伏个体L(t)以及谣言恢复个体R(t).谣言的传播过程如图1所示.

基于图1中的谣言传播规律,作如下解释:假设系统的移入率是B,每个仓室的移出率是µ.当易感个体S通过与谣言传播个体I进行接触,以α的概率听到谣言,易感个体就会有三种可能的选择:第一种选择是相信并传播谣言,从而以θ1的概率成为谣言传播个体;第二种选择是犹豫是否要传播谣言,从而以θ2的概率成为谣言犹豫个体H;第三种选择是不相信也不传播谣言,从而以(1−θ1−θ2)的概率成为谣言恢复个体R.在经过一段时间的考虑之后,犹豫个体H会有两种选择:犹豫个体可能由于被谣言吸引从而以mβ的概率变成谣言传播个体(m代表谣言的吸引性);也可能不被谣言吸引从而以(1−m)β的概率成为谣言恢复个体.而对于谣言传播个体而言,当谣言被验证是假消息时,他们就会变成谣言潜伏状态.潜伏状态的个体L可能完全失去了传播谣言的兴趣,从而以η的概率成为谣言恢复个体;也有可能以ϕ的概率再次变成谣言传播个体.

图1 SHILR谣言传播过程

综上所述,基于平均场理论,建立如下同质网络中具有谣言复发、复发时滞以及个体行为的SHILR谣言传播模型:

由于系统(1)的前四个方程独立于恢复个体R,为了方便起见,考虑如下等价系统:

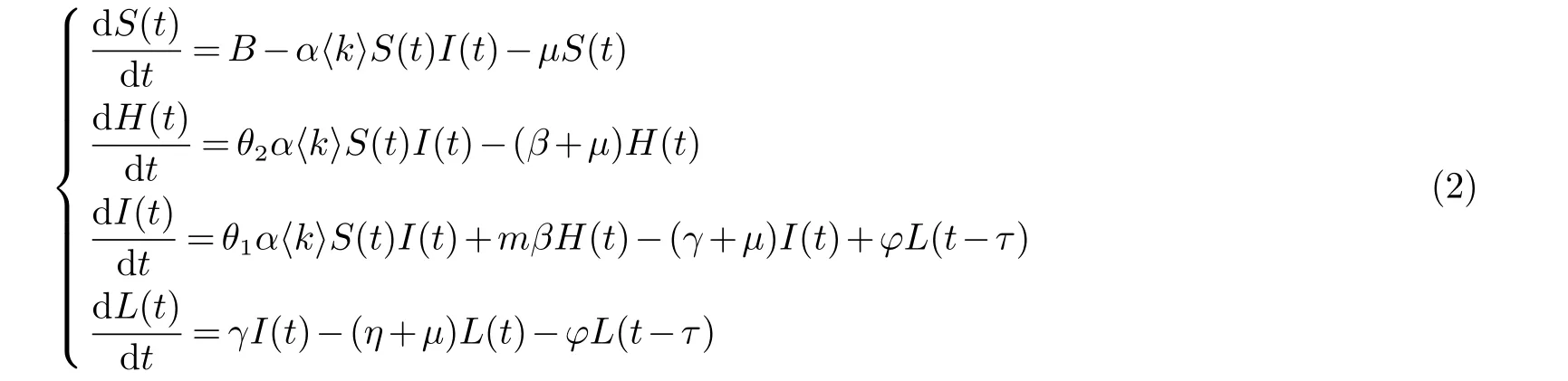
其中:B>0,µ>0,α>0,θ1∈(0,1),θ2∈(0,1),1−θ1−θ2∈(0,1),m>0,β>0,γ>0,ϕ>0,η>0.记N(t)是t时刻用户的总数,则N(t)=S(t)+H(t)+I(t)+L(t)+R(t).此外,系统还满足初始条件:S(t)=φ1(t)≥0,H(t)=φ2(t)≥0,I(t)=φ3(t)≥0,L(t)=φ4(t)≥0,t∈(−τ,0],其中φi(t)(i=1,2,3,4)是非负连续函数.

2 平衡点的动力学分析

众所周知,在传染病学领域,基本再生数R0表示在发病初期,当所有人均为易感者时,一个病人在其平均患病期内所传染的人数,它是判断疾病是否传播的重要阈值.类似的,在谣言传播的研究中,定义R0来判断谣言是否传播,并分析平衡点的存在性与稳定性.

定理1定义基本再生数

(i)若R0<1,则系统(2)存在唯一的无谣言平衡点E0=(Bµ,0,0,0).

(ii)若R0>1,则系统(2)存在唯一的谣言传播平衡点

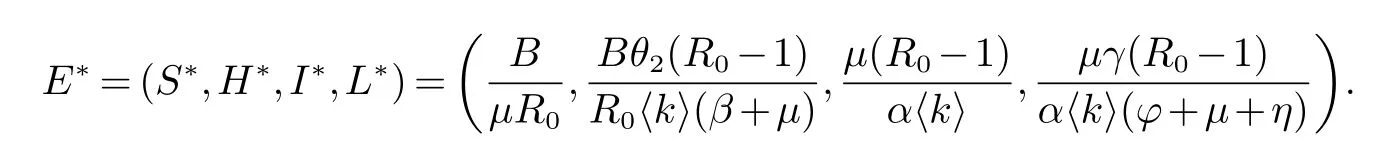
证明当系统(2)达到平衡时,各个仓室用户数量不再随时间的改变而改变.于是,令系统(2)等号右边为零,解如下方程:

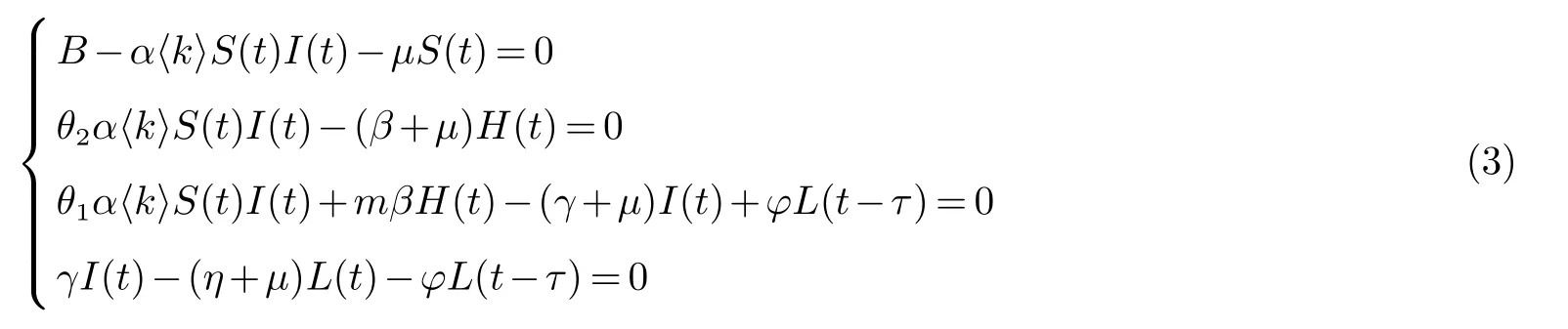
由于当谣言消失时,有I(t)=0.于是,将I(t)=0带入系统(2),可得S(t)=,H(t)=0,L(t)=0.因此,无谣言平衡点为E0=(,0,0,0).

此外,下面利用下一代矩阵法[21]求系统(2)的基本再生数.注意到,表示感染的仓室有H(t),I(t),L(t),对其进行重新排序为(H(t),I(t),L(t)).具有新感染的非线性项和剩余项分别为F和V,则

通过求解(5),得到唯一的谣言盛行平衡点E∗=(S∗,H∗,I∗,L∗)如下:

因此,若R0>1时,则系统(2)存在唯一的谣言传播平衡点E∗=(S∗,H∗,I∗,L∗).

定理2若R0<1,则系统(2)中的无谣言平衡点E0=(,0,0,0)是全局渐近稳定的.

证明构造如下Lyapunov泛函V1(t):

由此可见,在(7)中,当R0<1时,有 V˙1(t)≤0.此外,当且仅当S(t)=,H(t)=0,I(t)=0,L(t)=0时,有(t)=0.因此,根据LaSalle不变原理[22]可知:当R0<1时,系统(2)的无谣言平衡点E0是全局渐近稳定的.

定理3若R0>1,则谣言传播平衡点E∗=(S∗,H∗,I∗,L∗)是全局渐近稳定的.

证明构造如下Lyapunov函数V2(t):

其中,对于所有的n>0,有g(n)=n−1−ln n≥g(1)=0成立.令

3 数值模拟

本节通过数值实例验证理论结果的正确性,并分析时滞对谣言传播的影响．

3.1 无谣言平衡点的全局稳定性

为了证明定理2的有效性,选取系统(2)中的一组参数:n=200,B=0.02,α=0.2,β=0.1,γ=0.16,µ=0.02,θ1=0.15,θ2=0.2,η=0.2,ϕ=0.1,m=0.02,τ=2.在这组参数的取值下,有R0=0.771 4<1.从图2(a)中可以看到,如果R0<1,此时的谣言传播个体的数量会随着时间的流逝而最终消失.从图2(b)中可以看到,当R0<1时,从不同初始值出发的解都会收敛到无谣言平衡点E0,从而无谣言平衡点E0是全局渐近稳定的.

图2 无谣言平衡点E0的稳定性

3.2 谣言传播平衡点的全局稳定性

为了证明定理3的有效性,选取另一组参数:n=200,B=0.02,α=0.35,β=0.1,γ=0.2,µ=0.02,θ1=0.3,θ2=0.2,η=0.2,ϕ=0.1,m=0.4,τ=2.此时,有R0=2.664 4>1.谣言传播平衡点E∗的稳定性如图3所示.图3(a)表明,当R0>1时,谣言传播者的密度变化比较复杂,先下降后上升再下降,但是谣言的最终传播规模却是收敛到一个固定的常数.这就意味着谣言将继续盛行,谣言传播者的密度不为零.图3(b)表明,当R0>1时,从不同初始值出发的解都会收敛到谣言传播平衡点E∗,从而谣言传播平衡点E∗是全局渐近稳定的.

图3 谣言传播平衡点E∗的稳定性

3.3 时滞对谣言传播的影响

为了讨论复发时滞对谣言传播的影响,分别取τ为0,5,10,15,20,而其它参数与R0>1时所选取的参数一致.如图4所示,时滞的存在使得谣言的传播过程更为复杂,但是并不影响谣言传播的最终规模.

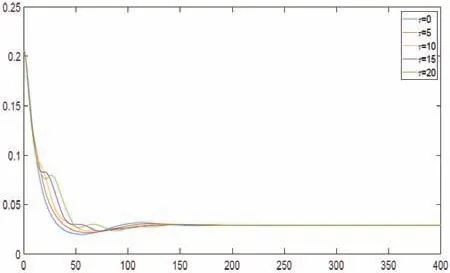
图4 时滞τ对谣言传播的影响

4 结论

本文综合考虑了谣言复发、复发时滞以及个体行为因素,建立了同质网络中具有时滞的SHILR谣言传播模型.首先,利用下一代矩阵法得到了基本再生数R0.其次,利用Lyapunov方法和LaSalle不变原理[22]分析了模型平衡点的稳定性.同时,数值模拟结果有效地验证了理论的有效性,最后分析了时滞对谣言传播的影响.结果表明,时滞的存在使得谣言传播的过程更为复杂,但不影响谣言传播的最终规模.此外,受到具有随机噪声[23]和分支现象[24]传染病动力学的启发,在同质和异质网络上研究随机扰动下的谣言传播以及研究具有分支现象的谣言传播动力学是今后有待研究和探讨的问题.