Fixed-Time Synchronization of Multi-Layer Networks via Periodically Intermittent Control∗

ZHAO Tingting,YU Juan,HU Cheng

(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830017,China)

Abstract: This paper is mainly concerned with the issue of fixed-time(FXT)synchronization of multi-layer networks by means of periodically intermittent control.By using the Lyapunov method,differential inequality and the FIT stability theorem,some sufficient criteria are derived to ensure the FIT synchronization of multi-layer networks,and an accurate estimate of the setting time is given by rigorous theoretical deduction.Ultimately,the feasibility of the developed control design and the established criteria is illustrated by a numerical example of the two-layer network.

Key words:fixed-time synchronization;periodically intermittent control;multi-layer network

0 Introduction

Complex networks usually consist of a large number of interconnected nodes,each node represents a dynamically evolving individual of a system in real life[1].However,it is difficult to describe many real-world networks via single-layer complex networks with the development of modern science and technology.For example,in the transportation network,people can choose a variety of travel tools,such as cars,trains,ships and airplanes,which results in a multi-layer network(MLN)[2].Unlike the single-layer complex network,the MLN contains more complex dynamic behavior and performance due to its complicated topological structure.Thereby,MLNs can better simulate real networks,such as social networks[3],ecological networks[4],neural networks[5−6],and so forth.

In general,control techniques have great influence on the realization of synchronization of networks.Hitherto,various control schemes have been used to study the synchronization of the MLNs,such as impulsive control[7],feedback control[8]and event-trigger control[9].The intermittent controller,first proposed by Zochowski[10],has higher execution speed and lower control cost compared with the continuous control design.On the other hand,realizing synchronous convergence in a finite time has the advantage of improving robustness[11].However,the establishment of the setting time for finite-time(FNT)synchronization depends on the initial states,which are not always available in practical applications.In order to overcome the difficulty,Polyakov introduced the concept of FXT convergence[12].At present,there is little research on the synchronization problem of MLNs by using intermittent control.The FNT synchronization problem of multi-layer coupled networks was studied based on periodic intermittent feedback control[13].Unfortunately,there is no related work to investigate FXT synchronization of MLNs based on intermittent control.Motivated by the above discussion,FXT synchronization of MLNs is studied by periodic intermittent control.By applying the differential inequality technique and the Lyapunov function method based on 1-norm,some sufficient conditions are derived to achieve the FXT synchronization of MLNs under periodically intermittent control.

The rest of this article is arranged as follows.First of all,some preliminaries are introduced in Section 1.The FXT synchronization is discussed in Section 2.Some numerical results are presented in Section 3 to illustrate the feasibility of the developed control scheme and criteria.Finally,the conclusion and the discussion for future research are given.

Notations:In this paper,R and Rnrespectively denote the set of all real numbers and then-dimensional Euclidean space.Rn×nis the set of alln×nreal matrices,={1,2,···,n},={1,2,···,ℵ}and={1,2,···,M}for positive integersn,ℵand M.For anyξ∈R,Sign(ξ)is the sign function ofξ.For anyζ=(ζ1,ζ2,···,ζn)T∈Rn,y=(y1,y2,···,yn)T∈Rnand θ>0,Sign(ζ)=(sign(ζ1),···,sign(ζn))T,[ζ]θ=(|ζ1|θ,|···,|ζn|θ)T,andζ◦y=(ζ1y1,ζ2y2,···,ζnyn)T.diag{·}stands for a diagonal matrix.

1 Problem Description and Preliminaries

Consider a class of MLNs composed of M layers,which is described by

wheres(t)denotes the state of the isolate node.

Assumption 1There exists a non-negative constantρsuch that for anyχ,y∈Rn,

Definition1 The multi-layer network(1)is said to be FXT synchronized to system(2),provided that there exists a positive constant T(ζ(0))such that

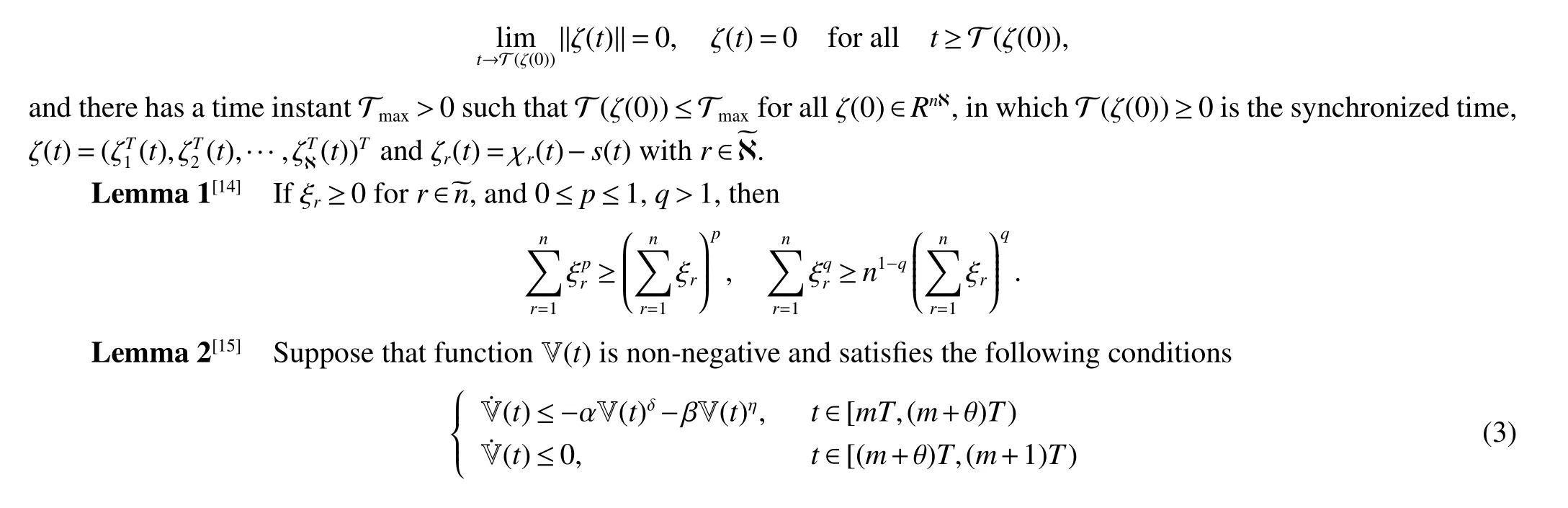
2 Fixed-Time Synchronization

In this part,we mainly study the problem of FXT synchronization of the MLN(1)through periodically intermittent control technology and FXT stability theory.

The periodically intermittent controller is designed as follows

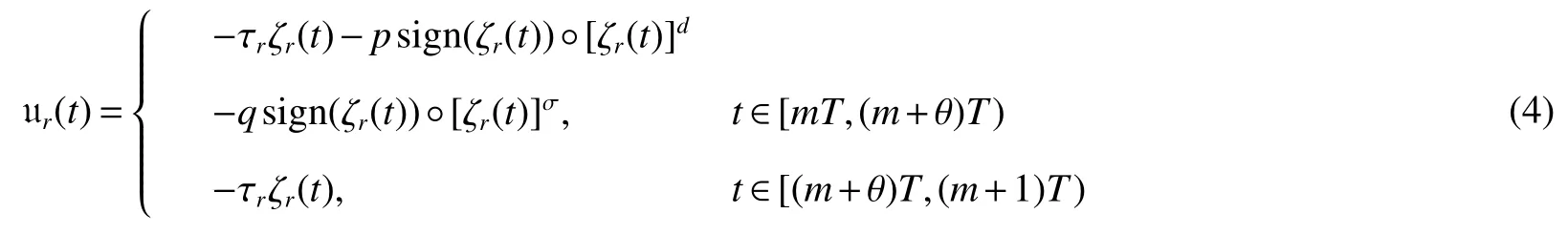
wherer∈p>0,q>0,01,T>0 represents the control period,0<θ<1 represents the ratio of the control width to the control period,which is called the control rate,andτrrepresents the control gain.

Letζr(t)=χr(t)−s(t),then the error system can be represented as follows

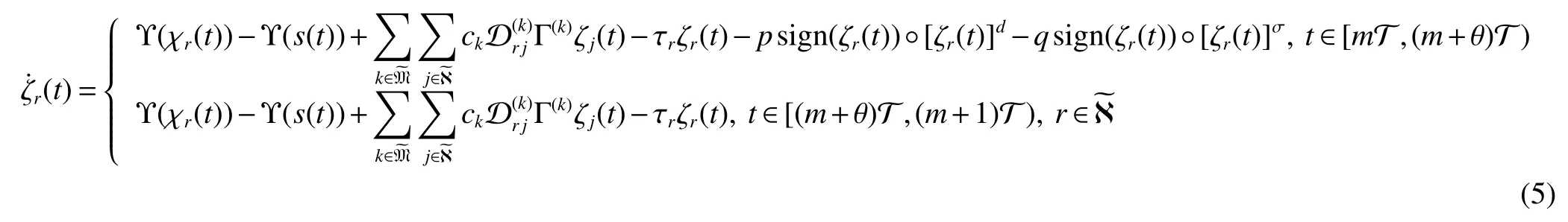
Theorem 1Under Assumption 1 and the control law(4),the MLN(1)is fixed-time synchronized if

whereEℵdenotes theℵ-dimensional identity matrix,and∆=diag(τ1,···,τℵ).Moreover,the settling time T(ζ(0))is estimated by

ProofConstruct Lyapunov function

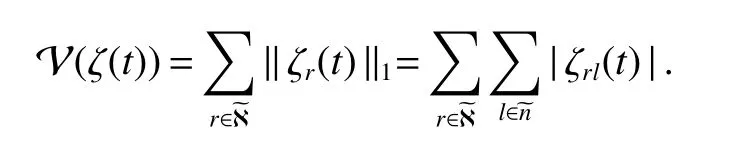
Forζ(t)∈Rnℵ{0},calculate the time derivative of V(ζ(t))along the trajectory of system(5).Whent∈[mT,(m+θ)T),one has

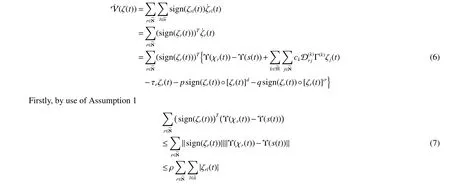
Note that

The proof is achieved.

Remark 1In Theorem 1,provided thatd=0,the estimate of T(ζ(0))is reduced to the following form

Remark 2It should be noted that when M=1,the MLN(1)will be transformed into a single-layer network as follows

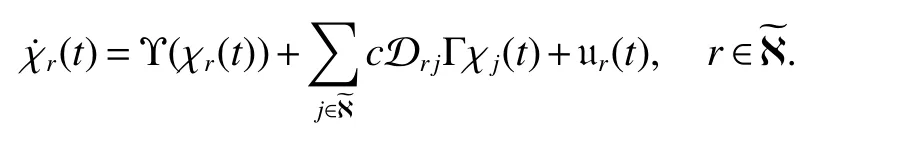
In this case,the condition in Theorem 1 is simplified to the following form

Whenq=0,the fixed time controller is converted to the following control scheme

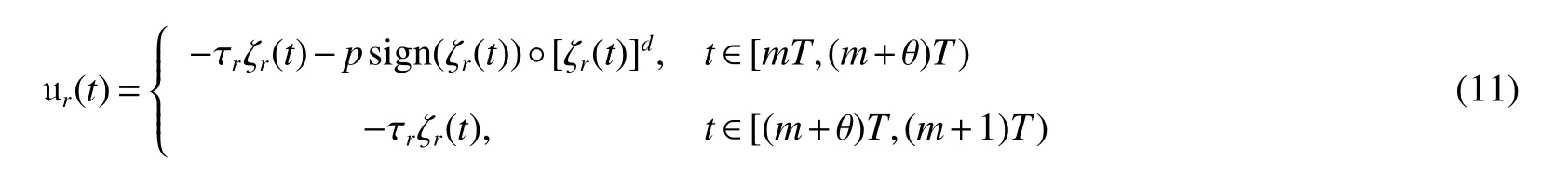
wherer∈p>0,q>0,00 is the control period,0<θ≤1 represents the control rate,andτrrepresents the control gain.

Corollary 1Under Assumption 1 and the intermittent control law(11),the MLN(1)is finite-time synchronized if

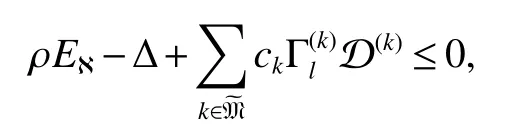
whereEℵdenotes theℵ-dimensional identity matrix,and∆=diag(τ1,···,τℵ).Moreover,the settling time T(ζ(0))is estimated by

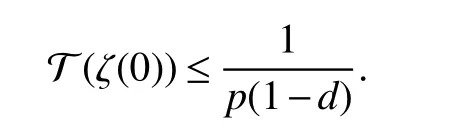
Whenθ=1,the periodically intermittent controller(4)is transformed into continuous control scheme

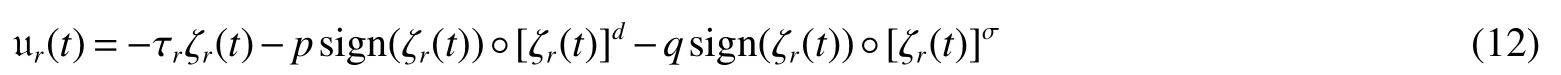
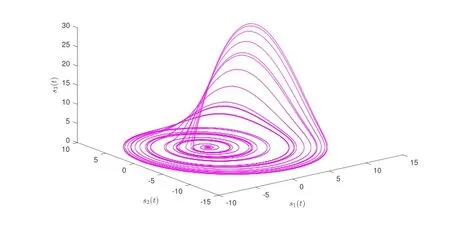
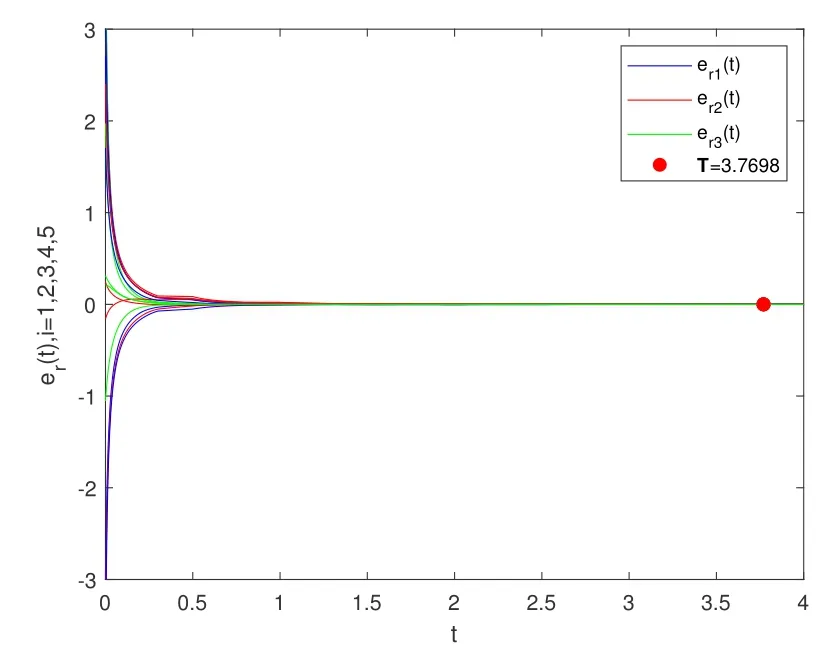
wherer∈p>0,q>0,0

Corollary 2Under Assumption 1 and the feedback control law(12),the MLN(1)is fixed-time synchronized if

whereEℵdenotes theℵ-dimensional identity matrix,and∆=diag(τ1,···,τℵ).Moreover,the settling time T(ζ(0))is estimated by

Remark 3In recent research work[7−8,13],scholars have studied the synchronization problem of MLNs by using different control strategies,but intermittent fixed-time control has not been considered.Therefore,the periodically intermittent fixed-time control is introduced in this paper,and some effective criteria are derived for the FXT synchronization of MLNs through intermittent control.

3 Numerical Example

To verify the above synchronization results,a numerical example and several related simulations are provided in this part.

Consider a two-layer dynamic network composed of 5 nodes.The controlled network is depicted by

whereΥ(χr)=(−0.8(χr2+χr3),χr1+0.2χr2,χr3(χr1−5.7)+0.2)T,c1=c2=0.1,Γ(1)=2E5,andΓ(2)=4E5.

The topology of the two-layer dynamic network(13)is shown in Fig 1.

Fig 1 Topology structure of multi-layer network(13)

Fig 2 Chaotic phenomenon of system(14)

In the following numerical simulations,R¨ossler system is chosen as the synchronized state,which is described as follows

The dynamical evolution of model(14)is simulated in Fig 2 with initial state(0.1,0.1,0.1)T.

By simple calculation,ρ=43.473 0.Chooseτr=45,for allr=1,···,5,θ=0.6,T=0.5,p=1,q=18,d=0.3 andσ=2.From Theorem 1,the controlled two-layer network(13)is fixed-time synchronized onto the model(14)and it is obtained that T=3.306 9.The corresponding simulation results are presented in Figs 3 and 4.

Fig 3 FXT synchronization for multi-layer networks(13)

Fig 4 The evolution of controller(4)

4 Conclusion

This paper has investigated the FXT synchronization of MLNs.By designing periodically intermittent controller and utilizing the Lyapunov function method,some sufficient conditions have been established to realize the FXT synchronization.These theoretical results are further verified by providing some numerical simulations.Nowadays,it is extremely scarce to analyze FXT synchronization for multi-layer dynamic networks via event-triggered control and sample-data control.These interesting problems will be investigated in future research.