基于浅埋暗挖法施工隧道的Peck公式反演分析

杨鸿瑞，张 波，马腾飞，殷 健，黄照斌，郭 敏

（中建二局第二建筑工程有限公司，广东 深圳 518000）

隧道工程施工中必然会对隧道围岩产生扰动，围岩变形及位移超过限值将威胁隧道主体结构及隧道周边环境的安全，地表沉降是公路隧道施工中的必测项之一。G344 汝州汝阳至洛峪段工程包含4 座分离式隧道，隧址浅埋段围岩较破碎，洞口边坡稳定性差，施工风险大。故此，施工时需要对浅埋段地表沉降的预测和监控量测引起重视。

隧道建设中进行地表沉降估算众多方法中，Peck 公式预测沉降曲线是目前应用最为广泛的方法。韩煊[1]通过对国内30 余组监测数据的总结，分析Peck 公式在各地区的适应性，并对相关参数的选取提出了初步建议。郭二新[2]依托常州地铁项目，通过线性回归修正Peck 公式，使之更适用于常州地域。王哲[3]针对浅埋暗挖施工隧道通过数值模拟方式分析不同埋深下的沉降槽宽度值，在杭州软土地区的应用中取得了良好效果。

然而，Peck 公式中的参数取值受地质环境影响，预测结果具有较大的差异性。针对其中的参数进行修正可提高Peck 公式预测结果的精度，从而更具指导意义。

本文基于G344 汝州汝阳至洛峪段中2 座隧道（紫罗山隧道）的实测数据，通过反演分析修正Peck 公式的沉降槽宽度系数和最大沉降量系数。对本地区后续修建隧道工程具有一定指导意义。

紫罗山隧道穿越的山体由下第三系陈家沟组石英砂岩组成，隧道进出口为强风，洞身主要穿越中风化、微风化花岗岩，浅埋段隧道的埋深为16～25m，岩层的最大内摩擦角φ＝25°。

1 Peck公式基本介绍及反演分析

Peck 学者于1969 年分析大量隧道地表沉降资料后提出，隧道开挖造成的地表沉降是在不排水条件下发生的，并且总结出了Peck 公式[4]，Peck 假设隧道掘进方向上地层的损失是均匀的。地面沉降的横向分布基本符合高斯曲线，沉陷槽横向分布如图1 所示。

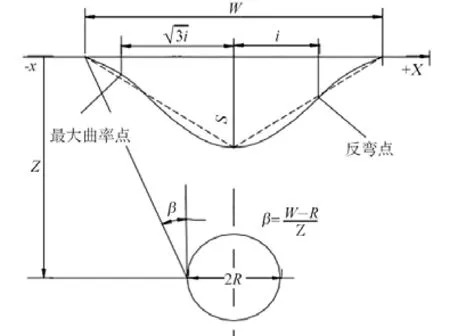
图1 沉降槽横向分布图

Peck 公式提出之后经过多位学者的不断完善，可列式如下。

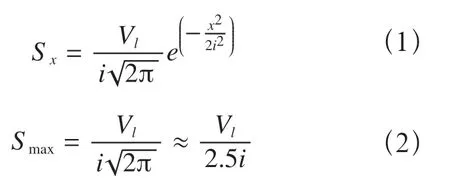
式中x——监测点或计算点到沉降中心线的水平距离（m）；

Smax——地表沉降曲线的最大值（mm），通常该点位于沉降曲线的中心线；

Sx——距隧道轴线水平距离为x处的地表沉降量（mm）。

Vl——隧道单位长度的地层损失率（%），Vl取值为0.8，

i——沉降曲线中心线至反弯点位置的水平距离（m），i的取值按照沉降宽度计算公式进行计算

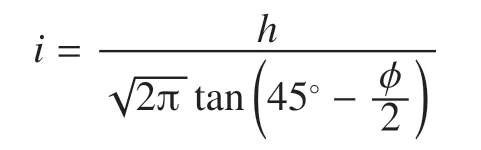
代入数据计算可得i＝11.896m

理论上最大沉降量为

Smax＝Vl/2.5i＝0.026900m＝26.9mm

可以得到此处地表沉降的理论公式

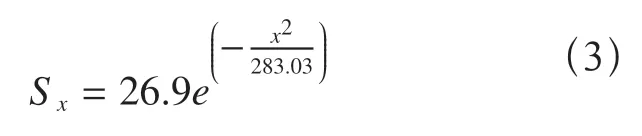
根据公式预测出该断面测点的理论沉降值，见表1。

表1 断面测点的理论沉降值 (单位：mm)

上述（1）式可写为以下形式

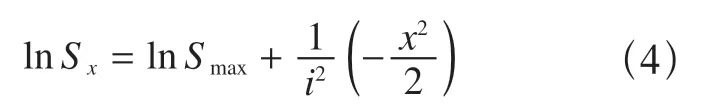
令a＝lnSx，b=，c＝lnSmax，d=，则简化后的公式可表达为a＝c+db，将地表沉降数据，运用最小二乘法进行拟合分析，可知其回归参数如下

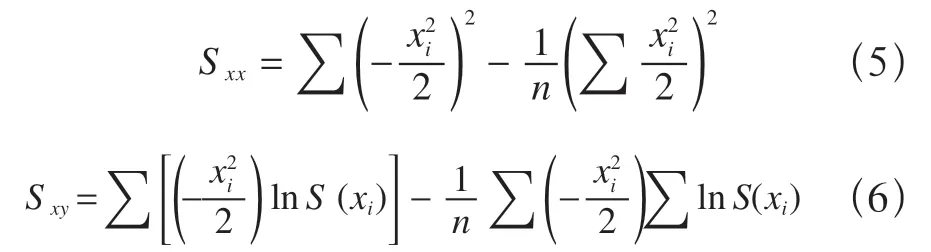
运用上述方法，可以得出Smax和i的最佳拟合参数如下

通过上述方法可拟合曲线，接着采用线性相关系数R判定回归函数的相关程度。

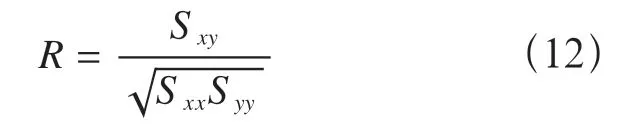
2 地表沉降数据回归分析

本文以G344 国道紫罗山隧道为研究对象，取紫罗山隧道左线3 个断面，右线1 个断面，每个断面取9 个样本点，样本点间距应为靠近中线布置密些，取值在2～5m 之间，单侧布置总宽度要大于反弯点到中线的距离，按照上述回归分析方法对其地表沉降数据进行回归分析，再对分析数据进行相应计算得到所需数据。其分析结果见表2。

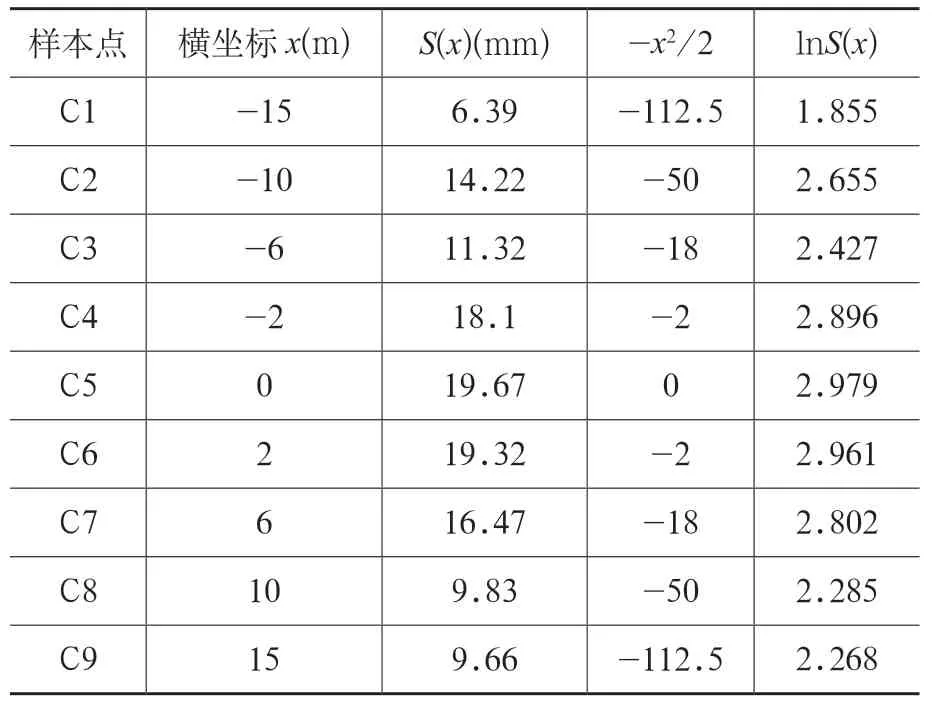
表2 ZK6+380断面地表沉降数据回归分析表

将表1 中的数据代入公式中计算可以得出Sxx＝16165.722，Sxy＝121.300，Syy＝1.192，c＝2.874，d＝0.0075，Smax＝17.708mm，i＝11.785m。将计算所得的实际数据代入到线性相关函数中，可以得到关于a、b的回归后线性函数

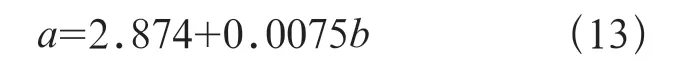
即得到相应的拟合公式，再用拟合公式算出拟合值，可以得到此断面的地表沉降实测值、拟合值和预测值，详见图2。

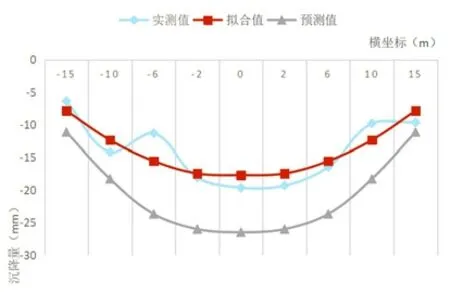
图2 ZK6+380处地表沉降各值

根据公式（12）求出线性相关系数R＝0.874，可认为回归函数线性显著相关。

3 Peck公式的改进

根据Peck 公式的计算参数，Peck 公式的改进，要考虑地质环境以及最大沉降量，通过将最大沉降量修正系数m和沉降槽宽度修正系数n引入原公式，可写为以下形式

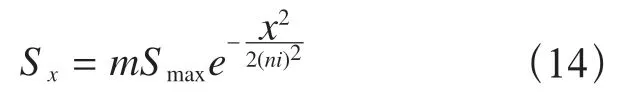
对式（14）两边同时取对数变为以下形式

将ln（mSmax）看作回归后的常数项，看作回归的线性系数，按第2 节所述过程计算，可得相应的c′和d′。

其中：

ZK6+380 断面地表沉降数据回归后所得系数为m＝0.658，n＝0.993。

选取隧道不同的断面进行分析，重复上述计算过程，得到相对应的修正系数，并对其进行分析。为了保证紫罗山隧道的作业安全，以及原地貌保护，故此应重视施工中地表沉降量的监控测量，尤其是隧道进、出洞口附近的隧道浅埋段。选取其他3 个断面的实测沉降值，用同样方法进行拟合后数据与实测数据对比，见表3。

表3 紫罗山隧道不同断面实测地表沉降值与拟合数据对比 （单位：mm）

根据各断面的拟合结果分别计算各断面的最大沉降量修正系数m和沉降槽宽度修正系数n，最终得到最大沉降量修正系数m取值范围为0.477～0.744，沉降槽宽度修正系数n取值范围为0.749～0.993。基于以上分析，可以较好预测工程所在地区的隧道施工引起的地表沉降。

4 不同埋深条件下地表沉降规律分析

G344 道路紫罗山浅施工隧道，左线长约498m，右线长约470m，隧址区属于山地丘陵区，掘进距离长，隧道浅埋段的覆土厚度在16～25m 之间，埋深有一定的变化。工程所在区域的地质环境稳定、地质条件变化不大。基于此认为沉降槽修正系数宽度变化不大。为方便分析，除隧道埋深外施工条件不变，认为地层损失率保持不变，各断面都取0.8。

针对浅埋段现选取16m、19m、25m 三个不同埋深断面进行地表沉降的理论计算，取最大沉降量修正系数m为0.6，取沉降槽宽度修正系数n为0.8，按照修正后的计算公式预测不同埋深沉降量，结果见图3 所示。

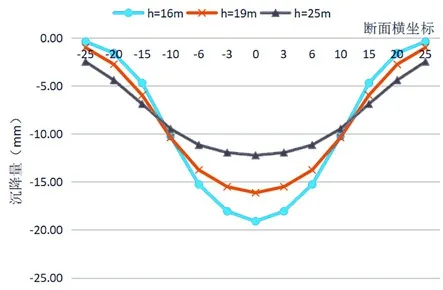
图3 不同埋深下的地表沉降示意图

由图3 可知，其他条件不变，随着隧道埋深的增大，最大地表沉降值逐渐减小，沉降槽宽度逐渐增大，呈“扁平”化趋势。

5 结论与展望

1）利用最大沉降量修正系数和沉降槽宽度修正系数后的Peck 公式可以更好地估计最大沉降量和影响范围。紫罗山隧道工程所在地区的推荐取值范围为最大沉降量修正系数m取值范围为0.477～0.744，沉降槽宽度修正系数n的取值范围为0.749～0.993。

2）本工程证明了Peck 公式在浅埋暗挖法的适应性。但样本量较小，修正系数的范围较大，不利于推广使用，因此拟在后续施工中进一步验证Peck 公式在浅埋暗挖隧道中的适用性，并收集监测数据以优化最大沉降量修正系数和沉降槽宽度修正系数的取值。

3）其他条件不变，随着隧道埋深的增大，最大地表沉降值减小，沉降槽宽度增大，呈“扁平”化趋势。