可加风险模型现状数据样本量的确定

2022-01-28孔令涛宋祥军王晓敏

广西师范大学学报（自然科学版） 2022年1期

孔令涛, 宋祥军, 王晓敏

(山东财经大学统计学院，山东济南 250014)

在经济学、人口学、流行病学和社会科学研究中，经常遇到现状数据或第一类区间删失数据[1-4]。上述研究中假定只能够观测一次，得到的信息是事件发生时间小于或者大于等于观测时间，这种数据称为现状数据。对于右删失数据，有可能观测到事件发生的准确时间，因此现状数据比右删失数据更加复杂和难以处理。下面给出现状数据的一个典型例子: 在艾滋病病毒研究中，研究者无法观察到病毒发展的准确时间，能够观测到的只是病毒在试验前还是试验后发展起来的，该数据就属于现状数据。

样本量计算是科学研究设计阶段的必要组成部分，其相关研究已经有非常优秀的成果[5-8]。对于右删失数据来说，文献[9]给出协变量为正态分布的逻辑斯蒂回归模型功效的计算结果;文献[10]在随机临床试验下对比例风险(PH)模型研究同样问题;文献[11]将文献[10]的工作推广到协变量与时间相关的比例风险模型。对现状数据而言，文献[12]对比例风险模型提出一种计算功效和样本量方法;文献[13]将比例风险模型推广到半参数变换模型[14]。注意到，上述研究工作主要集中在比例风险模型。然而，在实际应用中，比例风险模型往往不能很好地拟合实际数据，其替代模型之一是可加风险(AH)模型[3,14-16]，该模型假定协变量对基础风险函数具有加法影响。文献[14]指出可加风险模型在许多应用中较比例风险模型更加合理，特别是在双样本情况下。对于右删失数据的情况，文献[17]研究了右删失数据中不同参数设置下样本量及删失率的规律;文献[18]利用对数秩检验思想给出可加风险模型样本量的计算结果。对于现状数据下可加风险模型样本量的确定没有相关结果，这是本文研究问题的出发点。

本文剩余部分组织如下：第1章介绍具有现状数据的比例风险模型的极大似然估计，并基于Wald检验建立样本量的渐近结果；第2章研究累计时间和随访时间对功效的影响；第3章对所提出方法进行模拟研究；第4章给出一个基于肿瘤发生性研究的实际例子，验证样本量公式；第5章是结语;部分技术细节在附录中给出。

1 方法

考虑一个涉及n名患者的研究，令Ti、Ci、Zi分别表示第i个患者的发病时间、检查时间和相应的协变量。对现状数据来说，在检查时间对每位患者进行观测，而发病时间不能够被直接观测到，观测到的结果为{Yi=(Ci,Δi,Zi),i=1,…,n}，其中Δi=I(Ti≤Ci) 表示Ti是否大于Ci。给定协变量Zi，可加风险模型的风险函数具有如下形式

λ(t,Zi)=λ0(t)+βTZi,

式中：λ0(t)表示未知基础风险函数；β表示未知参数。本文假定删失机制是独立的和非信息的(见文献[19])。很明显，协变量对风险的变化具有加法效应。对任意t≥ 0，用

S(t)=S(t,Z)=P(T>t)=exp{-λ0(t)-βTZt}

(1)

假设对医学研究中两组之间的比较感兴趣，例如治疗(新研发药物与标准药物)或性别(男性与女性)，使用二元协变量Z表示组成员。为了测试不同组的影响，考虑下面假设检验

H0∶β=0↔HA∶β>0。

IA(β)=E{[ZC-g*(C)]2Q(C,Z)},

(2)

(3)

式中：Φ(·)表示标准正态分布的累计分布函数；Z1-α/2是标准正态分布的1-α/2分位数。因此，样本量可以由式(4)确定

(4)

一个特殊情况：考虑一个独立删失的情况，即观测时间与发病时间和协变量相互独立。用p=P(Z=1)表示治疗组占的比例，基础风险函数是一个常数λ0。用fC(·)表示删失时间的条件密度函数。因此，函数g*具有如下形式：

由等式(2)可知，IA(β)可以表示为

式中τa和τf分别表示累积时间和随访时间。注意，累积时间、随访时间、显著性水平、治疗组所占比例和观测时间的密度函数都是研究计划的一部分，因此，数值积分可以用R软件中的“integrate”函数来实现，可以通过将IA(β)带入到式(4)得到现状数据样本量的精确计算结果。

2 累积时间和随访时间的影响

本章研究累积时间和随访时间对功效的影响。基础风险函数设定为λ0(t)=0.5。假设观测时间服从均匀分布U(τf,τa+τf)，式中τf、τa分别表示累积时间和随访时间。假设治疗效果β=0.5，治疗组比例p=0.5。考虑显著性水平为0.05的双侧Wald检验。图1给出了AH模型的Wald检验的功效与长度的关系，其中样本量n=100、200、300。由图1可以观察到累积时间和随访时间对功效的影响比较复杂。图2给出了累积时间和功效的关系，很明显，功效和累积时间的关系是非线性、非单调且依赖于随访时间。例如，当随访时间为0.2 a(图2(a))或1 a(图2(b))时，功效先增大然后当累积时间超过某个时间点后开始减小(0.2 a对应的时间点为2.4 a，1 a对应的时间点为1.5 a)。当随访时间为5 a时(图2(c))，随着累积时间的增加，功效单调减小。随访时间对功效的影响类似于累积时间的影响，图3给出了随访时间与功效的关系，其中n=200。

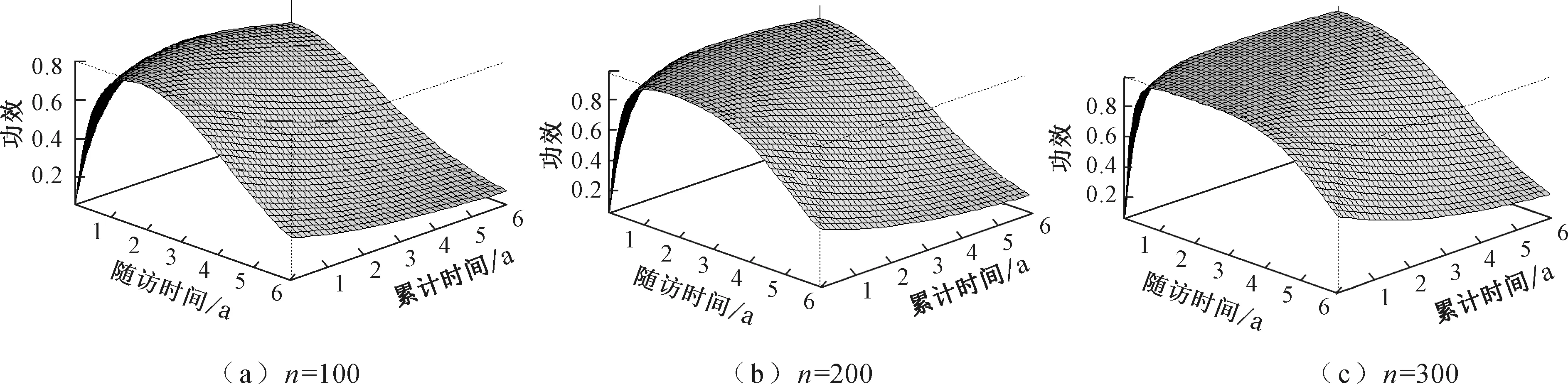
图1 n=100、200、300时不同累积时间和随访时间对应的理论功效

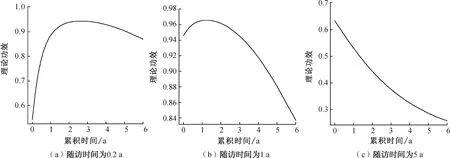
图2 n=200时3个不同随访时间下累积时间和功效的关系

图3 n=200时3个不同累积时间下随访时间与功效的关系

3 模拟研究

本章通过模拟研究考察样本量计算公式(4)的表现。假定观测时间和发病时间以及协变量是独立的。在模拟研究中，基础风险函数定义为λ0(t)=0.5，观测时间服从均匀分布U(τf,τa+τf)。考虑显著性水平为0.05的双侧Wald检验。此外，在模拟研究中，τf固定为10-4，而τa设置为3和5。治疗组比例p设定为0.3、0.4和0.5。研究β=0.3、0.5和0.7 这3种情况。对样本量n=50、100、150、200、250、300，模拟5 000个数据集并进行Wald检验。理论功效(TP)是根据等式(3)计算的，经验功效(EP)是进行Wald检验时被拒绝的比例，本文给出了两者的差。τa=3和τa=5 的模拟结果分别在表1和表2中给出。如果式(3)正确，则经验功效将非常接近理论功效，二者的差会很小。从表1和表2可以看出，经验功效和理论功效非常接近，故样本量的计算公式(3)表现非常好。对于平衡试验设计(p=0.5)，当n≥200时，在大多数情况下偏差的绝对值都会小于等于0.02。另外，对于非平衡的试验设计(p=0.3、0.4)偏差会稍微变大一些。本文得到的结果和文献[18, 21]的结果一致。

表1 α=0.05，τa=3时Wald检验的理论功效(TP)和经验功效(EP)对比

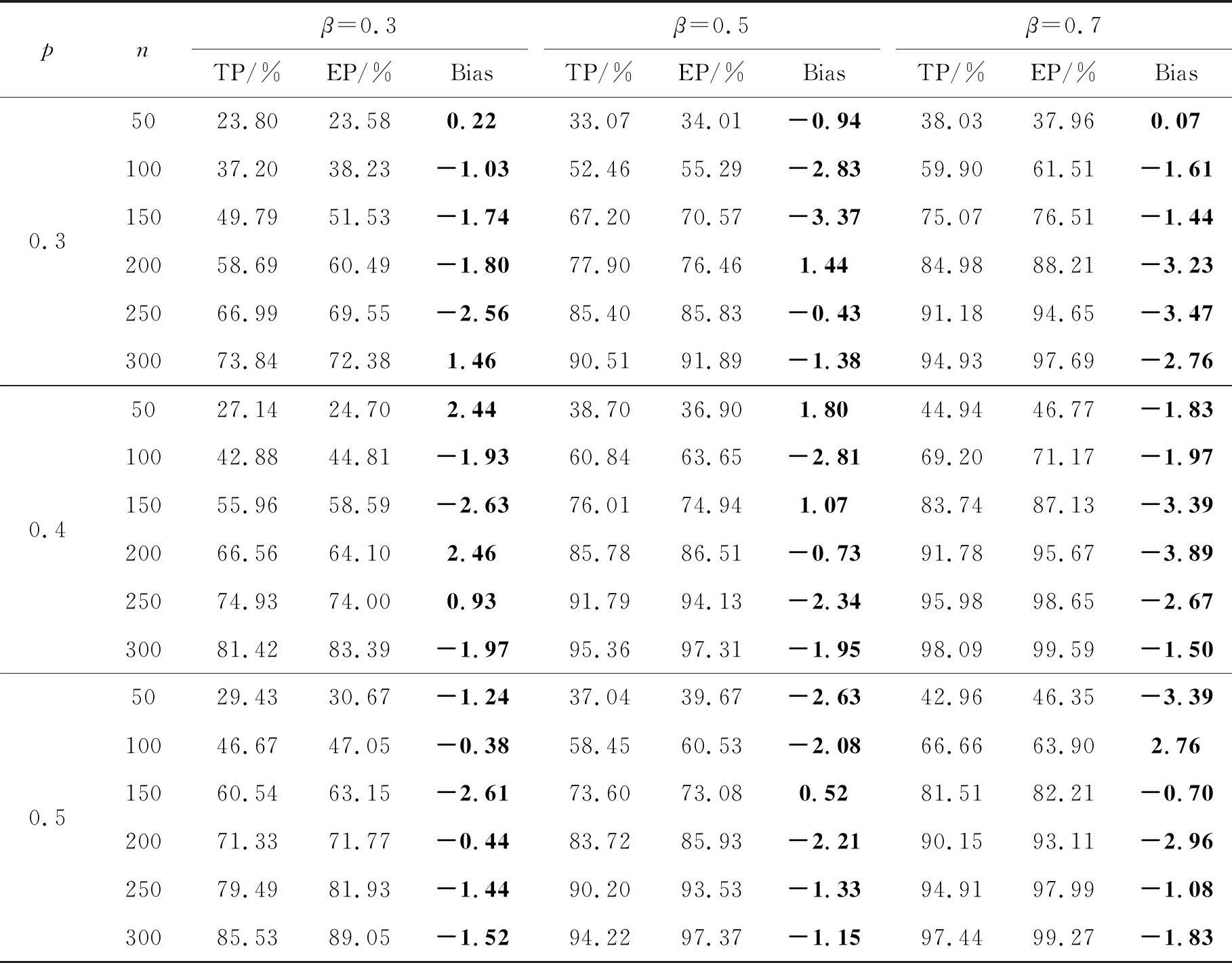
表2 α=0.05，τa=5时Wald检验的理论功效(TP)和经验功效(EP)的对比

4 实际例子

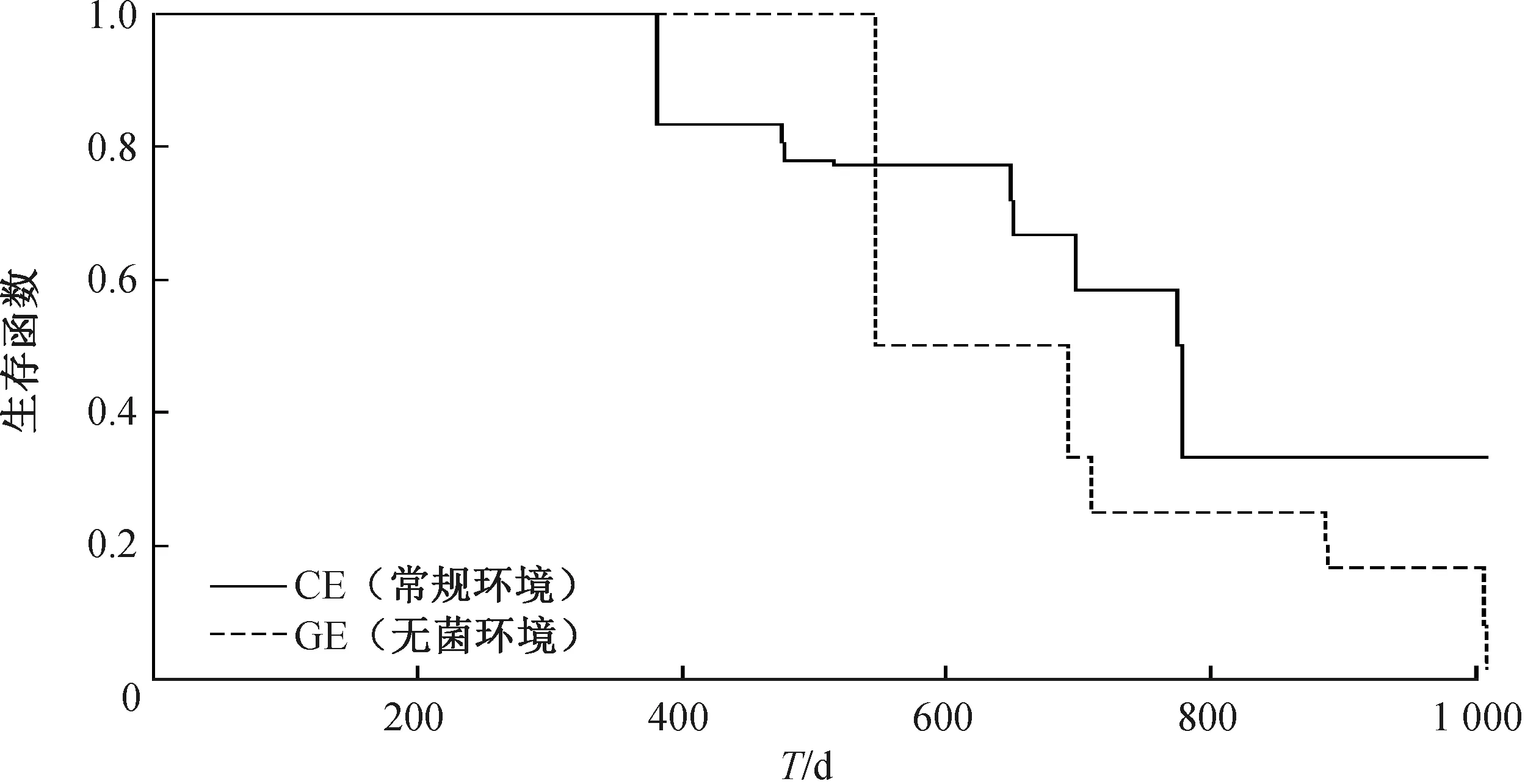
图4 雄性小鼠致瘤性研究数据的生存函数曲线

5 结语

本文基于Wald检验提出1个可加风险模型现状数据样本量计算的新方法，是比例风险模型和半参数变换模型样本量计算公式的推广(见文献[12-13])。给定显著性水平、功效、治疗组比例、观测时间的分布函数以及累积和随访时间，试验所需要的样本量就可以在研究的设计阶段进行确定。模拟结果表明：在不同情况下，本文提出的样本量的公式具有很好表现。此外，本文也将提出的方法应用到1个真实的数据集。

附录β的充分信息量

类似于式(2)，现状数据下可加风险模型一个观测值的对数似然函数为

l(θ)=l(θ|Y)=-(1-Δ)[λ0(C)+βTZC]+Δln[1-S(C,Z)],

式中：θ=(β,Λ0)；Y=(C,Δ,Z)。因此，β的得分函数具有如下形式