犁体耕作阻力模型仿真分析与试验研究

刘进宝，郑 炫，孟祥金，杨怀君，张鲁云，李清超

(1.新疆农垦科学院机械装备研究所，新疆 石河子 832000；2.石河子大学机械电气工程学院，新疆 石河子 832000)

由于新疆农田耕作土壤与东北黑土地的差异性，以及种植作物及模式的不同，不能完全照搬东北地区保护性耕作模式，犁耕、深松、秸秆还田深翻等机械化耕作对新疆盐碱化贫瘠土壤的改良具有促进作用，因此当前对新疆贫瘠土壤的犁耕机械化改良也显得尤为重要。随着土壤保护、改良技术的不断推进，犁耕作业对土壤的扰动、深度交换、能量消耗等方面技术重新得到重视。犁体是当前土壤耕作的主要部件之一，可将土壤疏松并使上下耕层土壤进行交换，具有很好的土壤翻垡和覆盖性能[1-7]。

犁体在耕作土壤时，产生的能量消耗是巨大的，据相关资料统计，耕地能耗占农机总能耗的50%左右[8-9]。犁耕阻力与犁体几何特征、性能参数、工作参数、土壤特性等参数密切相关，为了提高犁体性能，降低耕作阻力，国内外学者在犁体耕作阻力和减阻降耗和耐磨延寿等方面做了大量研究[10-14]。

林金天等[15]研究表明，耕作土壤主要的破坏形式是剪切破坏，剪切强度由粘结力和内摩擦力决定。区颖刚等[16]对塑性土壤不同破碎方法进行了比较，表明犁体曲面对土壤的破坏形式主要是剪切失效。李汝莘等[17]通过分析土壤容重、含水量与耕作阻力的关系，利用回归方程建立了耕作阻力与土壤容重及含水量的关系模型。朱新民等[18]通过经验公式，建立了包括犁铧切土阻力、弯曲剪切力、正压摩擦力等因素的犁体阻力模型。Gill等[19]通过试验研究表明，犁体耕作阻力随着耕作速度平方值的增加而增加。Oskoui等[20]建立了包含土壤圆锥指数的耕作阻力方程，通过模型预测和试验研究表明误差控制在合理范围。Qiong等[21]建立了犁耕阻力关于耕作速度的二次函数，其中包括了土壤含水率因素。Seig等[22]建立了包括犁体几何参数和土壤特性的耕作阻力数学模型，Saunders等[23]和Godwin等[24]又将耕作速度加入了该预测模型。

从当前的研究来看，国内有关犁体理论的研究基本停留在20世纪80年代前后[25-28]，一些学者提出的方法没有随着技术的发展进一步研究。国外相关研究已建立了包括土壤特性、犁体曲面几何参数和耕作速度的犁体耕作阻力模型，奠定了相关理论基础。当前犁具朝着宽幅、高速的方向发展，以现有研究基础考虑的因素还不够全面，有待进一步完善相关理论研究。因此，本文根据包含犁铲尖和犁铧的组合式犁铧结构构成的犁体，提出将犁体看做犁铲尖、犁铧、犁壁、犁侧板4个部分，并基于摩尔-库仑土壤剪切理论，建立犁体在耕作方向上的耕作阻力模型，立足西北干旱地区典型土壤，进行理论与试验研究，为犁体减阻降耗提供理论依据。

1 犁体耕作阻力模型

1.1 铲齿—土壤剪切理论

依据Godwin等[29-30]提出的摩尔-库仑土壤剪切理论的铲齿结构阻力模型(图1)，铲齿沿着速度v前进时，铲齿前方三角形ABC区域土壤对铲齿产生阻力(P)，可以分为水平方向的力(Fx)和垂直方向的力(Fy)。在土壤无其他外力施加的情况下：

图1 铲齿受力示意图Fig.1 Force diagram of shovel teeth

Fx=(γd2Nγ+cdNca)[y+d(m-(m-1)/3)+

γv2Nadc(yc+0.6dc)]sin(α+δ)

(1)

Fy=(γd2Nγ+cdNca)[y+d(m-(m-1)/3)+

γv2Nadc(yc+0.6dc)]cos(α+δ)

(2)

式中,ϒ为土壤容重(kg·m-3)；c为土壤内聚力(kN·m-2)；d为铲齿入土深度(m)；y为铲齿宽度(m)；m为土壤断裂宽深比；v为前进速度(m·s-1)；α为铲齿倾角(°)；δ为土壤与材料间的摩擦角(°)；Nϒ、Nca、Na为土壤无量纲常数。

因此阻力(F)为：

F=(γd2Nγ+cdNca+γv2dNa)y

(3)

1.2 耕作阻力模型

Saunders等[23]利用上述方法建立并完善了犁体阻力模型，本文以该模型为依据，将犁体阻力看作由犁铲尖、犁铧、犁壁、犁侧板4个部分所受力之和，包括犁铲尖、犁铧切削土壤产生的阻力，犁壁翻垡土壤产生的摩擦力和翻转土壤产生的阻力，犁侧板产生的摩擦力等，犁体受力情况如图2所示。

1.犁铲尖;2.犁铧;3.犁壁;4.犁侧板1.plough tip;2.plough share;3.plough mold board;4.plough side plate图2 犁体耕作受力示意图Fig.2 Diagram of ploughed soil resistance

犁体在水平面xoy坐标系中，沿着x轴反方向进行犁耕作业，假设犁体以速度v匀速前进，耕地过程中，土壤对犁体产生沿着运动方向上所受的合力是犁体所受的耕作阻力。建立基于摩尔-库仑土壤剪切理论的耕作阻力模型，包含了土壤特性参数(土壤容重、土壤内聚力、土壤抗剪强度、土壤间的摩擦角、土壤与犁体材料间的摩擦角)，犁体几何参数(犁铲尖和犁铧有效工作宽度、犁壁有效工作长度、犁侧板长度)，犁体工作参数(耕深和耕宽)，和犁耕作业速度等参数。沿着运动方向犁体耕作阻力(Fz)：

Fz=Fc+Fhx+Fbx+Fe+Fhf+Fbf+Fsf

(4)

式中,Fc为犁铲尖切削土壤阻力(kN),Fhx为犁铧切削土壤阻力(kN),Fbx为土壤在犁壁上产生的摩擦力和翻垡过程土壤动量变化产生的阻力(kN),Fe为犁壁翻垡使土壤势能增加产生的阻力(kN),Fhf为作用在犁铧上的横向力产生的摩擦力(kN),Fbf为作用在犁壁上的横向力产生的摩擦力(kN),Fsf为土壤横向运动对犁壁产生的阻力(kN)。

各分力表达式如下依次列出，具体过程见文献[17]、[24]。

Fc={(γdc2Nγ+cdcNca)[yc+

0.55dc(m-(m-1)/3)]+

(γv2Nadc/g)(yc+0.33dc)}sin(αc+δ)

(5)

式中,dc为犁铲尖入土深度(m)；yc为犁铲尖宽度(m)；v为犁体耕作前进速度(m·s-1)；g为重力加速度(m·s-2)；αc为犁铲尖倾角(°)。

Fhx=(γdh2Nγ+cdhNca+

γv2Nadh/g)yhsin(αh+δ)sinβ

(6)

式中,dh为犁铧入土深度(m),yh为犁铧宽度(m),αh为犁铧倾角(°),β为铧刃与运动方向的夹角(°)。

Fbx=(γ/g)(ycdc+yhdh)v2[1-(1-sinθtanδ)cosθ]

(7)

式中,θ为犁壁与运动方向的平均夹角(°)。

Fe=2γ(ycdc+yhdh)dh

(8)

Fhf=Fhytanδ=(γdh2Nγ+cdhNca+γv2Nadh/g)×

yhsin(αh+δ)cosβtanδ

(9)

Fbf=Fbytanδ=(γ/g)(ycdc+yhdh)v2sinθ×

(1-sinθtanδ)tanδ

(10)

Fsf=lγ(ycdc+yhdh)tanφstanδ

(11)

式中,l为犁壁工作长度(m)，φs为土壤间的摩擦角(°)。

以上的犁体耕作阻力模型，主要由犁体切削土壤产生的切削力、犁壁翻垡土壤产生的阻力，以及由侧向力产生的摩擦力组成，建立了包含犁体几何参数、工作参数、作业速度以及土壤物理特性的数学模型，根据公式(4)～(11)，在特定系数条件下可以预测犁体耕作阻力(Fz)。

1.3 土壤特性系数的确定

(1)土壤断裂宽深比(m)。土壤断裂宽深比即铲齿前段土壤以一定的形状被破坏，断裂区横向与纵向尺寸比值，表达式：

(12)

式中,f为土壤水平方向断裂距离(m)，d为纵向断裂距离。

此参数决定了土壤在耕作中被破坏的几何形状，如图1所示，根据Godwin等[32]的研究，得出土壤断裂宽深比(m)与铲齿倾角(α)呈非线性关系，并绘制了关系曲线，根据曲线列举了表1中对应值，供后续计算使用。

(2)土壤无量纲常数Nϒ、Nca、Na。Nϒ为土壤重力系数，Nca为土壤粘结系数，Na为土壤惯性系数，这些系数也是由土壤在耕作中被破坏的几何形状决定的，根据Hettiaratchi等[33]的研究结果，分别选取对应的系数值，见表1所示。

表1 土壤特性系数Table 1 Coefficient of soil properties

2 犁体耕作仿真分析

2.1 仿真模型的建立

利用EDEM离散元仿真软件进行犁体耕作阻力仿真分析，首先确定犁体材料和土壤特性参数，其次建立犁体曲面三维模型，设定工作状态，然后在颗粒工厂生成颗粒，最后运行计算，生成仿真结果数据。根据试验田实际土壤条件，将耕层土壤分为耕作层、犁底层和心土层，耕作层深度在0～150 mm之间，犁底层深度在150～250 mm之间，心土层深度在250～400 mm之间。采用Hertz-Mindlin和JKR粘结接触模型，可以更加真实地模拟土壤颗粒结构情况。土壤物理特性参数根据前期研究给定[34]，具体参数见表2所示。

表2 土壤物理特性参数Table 2 Soil physical properties parameters

试验犁体选用适合西北干旱地区耕作土壤的犁体，根据前期研究筛选出性能较好的两种犁体A和犁体B，利用逆向工程三坐标测量仪测出犁体样板曲线，并利用Solidworks软件绘制三维模型。犁体三维结构如图3所示，仿真时为提高运算速度简化模型，将犁铲尖、犁铧、犁壁和犁侧板看做一个整体，仿真模型如图4所示。

图3 犁体三维结构Fig.3 Three dimensional structure of plough body

图4 犁体仿真模型Fig.4 Plough body simulation model

两种犁体结构参数见表3所示。

表3 犁体结构及工作状态参数Table 3 Plough structure and working state parameters

犁铲尖实际工作宽度(yc)：

yc=yc0sinβ

(13)

犁铧实际工作宽度(yh)：

yh=yh0sinβ

(14)

两种试验犁体采用的是相同的材料，材料采用65Mn，泊松比为0.3，剪切模量为7.9×1010Pa，密度为7 865 kg·m-3。

2.2 试验方案设计

根据犁体结构及实际工作状态，耕宽分别设置为0.35 m和0.42 m，耕深分别设置为0.255 m和0.305 m，耕作速度分别设为2.22、2.5 m·s-1和2.78 m·s-1，共12组试验(表4)，在相应状态下分别进行仿真分析。

表4 试验方案Table 4 Parameter design of test scheme

2.3 仿真结果

通过运行仿真模型，土壤颗粒在犁体的作用下发生运动，如图5所示，从第3秒开始犁体入土，耕作阻力也会相应地产生变化，可以看出，随着犁体开始进入土壤并继续运动过程中，犁体所受的阻力在逐渐增加，当犁体完全进入土壤后，耕作阻力逐渐稳定。

图5 土壤颗粒运动状态Fig.5 Movement state of soil particles

根据仿真数据结果，进行单因素试验数据分析，分别得出犁体耕作阻力与耕深、耕宽、耕速的变化曲线，并与理论计算值和试验值进行比较，仿真数据见表5。同时可以看出犁体对土壤颗粒的扰动情况和流动速度。

3 田间试验

3.1 试验条件与方法

2019年9月，在新疆石河子市五工村玉米地进行了单铧犁体耕作阻力试验，仿真分析中的土壤在此地采集取样，测定了土壤特性参数，土壤类型为砂壤土，粘性较小，0.5 m土层深度内的土壤含水率在17.3%～40.1%，其中0～0.35 m耕层土壤平均含水率为20.6%，耕层在0.35 m内的土壤坚实度小于0.37 MPa，土壤容重1 435 kg·m-3，平均内聚力18.9 kN·m-2。试验区土地平整，残留玉米分布均匀。配套动力为雷沃欧豹904轮式拖拉机，阻力测量采用黑龙江省农业机械工程科学研究院研制的犁具专用遥测仪采集器，如图6所示。

遥测仪采集器通过悬挂式连接方式将犁具与拖拉机连接，共有上拉杆传感器、左下悬挂传感器和右下悬挂传感器3组数据采集传感器，由上拉杆传感器与左、右两个下悬挂销传感器测得的3处牵引力的矢量之和即为犁体水平面的耕作阻力。

试验方案与仿真分析方案一致，根据试验区域耕作农艺要求，以耕宽(0.35、0.42 m)、耕深(0.255、0.305 m)、耕作速度(2.22、2.5、2.78 m·s-1)为试验因素，以犁体耕作阻力为试验指标，采用单因素的试验方法，研究各因素对犁体耕作阻力的影响。

3.2 结果与分析

3.2.1 耕作阻力计算误差分析 根据试验方案，每组试验测量3组数据，取其平均值，将仿真分析得出的阻力值、试验测试的阻力值与理论计算值进行比较，分析仿真值与计算值、试验值与计算值之间的误差，数值见表5。

表5 犁体耕作阻力值Table 5 Ploughed soil resistance value

Ef=|Fzf-Fz|/Fz

(15)

Es=|Fzs-Fz|/Fz

(16)

Efs=|Fzs-Fzf|/Fzf

(17)

1.数据采集器;2.上悬挂传感器;3.下悬挂传感器1.data collector;2.upper suspension sensor;3.lower suspension sensor图6 田间试验Fig.6 Field experiment

式中,Ef为犁体耕作阻力仿真值与计算值的误差(%)；Es为犁体耕作阻力试验值与计算值的误差(%)；Efs为犁体耕作阻力试验值与仿真值的误差(%)；Fz为犁体耕作阻力计算值(kN)；Fzf为犁体耕作阻力仿真值(kN)；Fzs为犁体耕作阻力试验值(kN)。

根据犁体A与犁体B的耕作阻力计算分析，其中，犁体A仿真值与计算值的平均误差(Ef)为3.37%，最大误差为5.1%，试验值与计算值的平均误差(Es)为7.18%，最大误差为10.8%，试验值与仿真值的平均误差(Efs)为3.71%，最大误差为9.4%。犁体B仿真值与计算值的平均误差(Ef)为4.23%，最大误差为5.6%，试验值与计算值的平均误差(Es)为7.92%，最大误差为13.8%，试验值与仿真值的平均误差(Efs)为3.55%，最大误差为9.9%。由此可以看出，理论计算值与试验值的误差要大于与仿真值的误差。

总体来看，在相同试验条件下，犁体耕作阻力分析的数值从大到小依次是试验测量值、仿真分析值和理论计算值，平均误差均在合理范围，如图7所示。其中图7a、7b分别是犁体A计算值与试验值相关性和计算值与试验值相关性分析，图7c、7d分别是犁体B计算值与试验值相关性和计算值与试验值相关性分析，理论计算和仿真分析预测与试验测量值比较吻合，相对误差较小，预测值与试验值相关性较好。

图7 犁体耕作阻力计算值、仿真值与试验值的相关性Fig.7 Correlation between calculated,simulation and test value of ploughed soil resistance

3.2.2 犁体结构参数与耕作阻力的关系 根据建立的犁体耕作阻力模型，与犁体结构相关的参数有犁铲尖宽度(yc)、犁铧宽度(yh)、犁铲尖倾角(αc)、犁铧倾角(αh)、犁壁工作长度(l)、犁壁与运动方向的平均夹角(θ)、犁体材料与土壤间的摩擦角(δ)等。其中犁铲尖宽度和犁铧宽度与耕作阻力7个分力均相关，当在其他参数确定的前提下，耕作阻力与犁铲尖宽度和犁铧宽度呈线性增长的关系。犁铲尖倾角(αc)主要影响犁铲尖切削土壤阻力大小，并且与犁铲尖倾角(αc)的正弦值呈线性增长的关系。犁铧倾角(αh)主要决定分力犁铧切削土壤阻力和作用在犁铧的横向力产生的摩擦力，犁铧倾角正弦值与两个分力均呈线性增长的关系。犁壁与运动方向的平均夹角(θ)决定土壤在犁壁上产生的摩擦力和翻垡过程土壤动量变化产生的阻力和作用在犁壁上的横向力产生的摩擦力。犁壁工作长度(l)主要决定土壤横向运动对犁壁产生的阻力。犁体材料与土壤间的摩擦角(δ)影响着每一个分力的大小，而且也决定了土壤相对犁体的运动形式和过程。

按照以上犁体结构参数与阻力之间的关系，在以水平直原线、倾斜直原线、曲原线等设计方法设计犁体时，选取设计参数时，可以充分考虑该参数对耕作阻力的影响，从而设计出既能达到耕作要求又能降低耕作阻力的目的。

3.2.3 耕宽与耕作阻力的关系 在犁体结构确定的情况下，分析耕作阻力模型，得出耕宽与耕作阻力的变化关系，以犁体B在耕速2.5 m·s-1、耕深0.255 m时工作情况为例，阻力变化情况如图8a所示，犁体耕作阻力随着耕宽的增大呈非线性增长关系。

分析耕作阻力模型发现，在犁体结构参数确定的情况下，耕宽主要由改变铧刃与运动方向的夹角(β)来进行调节，因此，进一步分析铧刃与运动方向的夹角(β)与耕作阻力的变化情况，如图8b所示，关系表达式:

图8 犁体B阻力随耕宽及夹角的变化Fig.8 Resistance of plough body B varies with tillage width and included angle

Fz=k1sin2β+k2sinβ+k3sinβsin(90°-β)+k4

(18)

调幅犁在犁耕作业过程中，根据实际工况和作业需要，可以进行整机耕宽的调节，单铧犁的耕宽调整就体现在铧刃与运动方向的夹角(β)的改变，夹角(β)不易过大也不易过小，一般在35°～45°左右[1]，夹角(β)过小时耕宽太窄，造成后一铧犁体对前一铧犁体耕后土壤的重复耕作，浪费动力的消耗。夹角(β)过大时造成犁体大面积对土壤产生切削推土作用，根据阻力模型分力看出，此时阻力增长较大，动力消耗较大。

3.2.4 耕深与耕作阻力的关系 根据犁体耕作阻力模型推导结果，阻力与耕深呈三次函数关系。

Fz=b1d3+b2d2+b3d+b4

(19)

式中，系数b1、b2、b3、b4的值取决于土壤性质和犁的几何参数。根据本文试验研究的两种犁体A(耕宽0.35 m)和犁体B(耕宽0.42 m)，以及试验田土壤参数，分析预测在不同速度下不同耕深对应的耕作阻力值以及关系曲线(图9、10)。根据耕作阻力模型推导出犁体A和犁体B在不同耕作速度(2、2.5、3、3.5、4 m·s-1)下，耕作深度从0.15 m增加至0.35 m时犁体耕作阻力的增长变化情况。

图9 犁体A阻力随耕深变化关系Fig.9 Relationship between plough A resistance and depth

图10 犁体B阻力随耕深变化关系Fig.10 Relationship between plough B resistance and depth

3.2.5 耕速与耕作阻力的关系 根据犁体耕作阻力模型推导结果，阻力与耕速呈二次函数关系。

Fz=q1v2+q2v+q3

(20)

式中，系数q1、q2、q3的值取决于土壤性质和犁的几何参数。根据两种犁体A(耕宽0.35 m)和犁体B(耕宽0.42 m)，以及试验田土壤参数，分析预测在不同耕深作业条件下不同耕速对应的耕作阻力值以及关系曲线(图11、12)。根据耕作阻力模型推导出犁体A和犁体B在不同耕作深度(0.15、0.2、0.25、0.3、0.35 m)下，耕作速度从2 m·s-1增加至4 m·s-1时犁体耕作阻力的增长变化情况。

图11 犁体A阻力随耕速变化关系Fig.11 Relationship between plough A resistance and speed

图12 犁体B阻力随耕速变化关系Fig.12 Relationship between plough B resistance and speed

3.2.6 功率消耗与配套动力 在已知犁体结构、土壤特性和耕宽、耕深和耕速的前提下，根据上述分析可以确定犁体耕作阻力，此时，单铧犁体消耗功率(Pz)为:

Pz=Fzv

(21)

根据公式(20)，单铧犁体功率消耗与耕作速度呈三次函数关系:

Pz=q1v3+q2v2+q3v

(22)

根据两种犁体A(耕宽0.35 m)和犁体B(耕宽0.42 m)，分析在不同耕作深度(0.15、0.2、0.25、0.3、0.35 m)下，耕作速度从2 m·s-1增加至4 m·s-1时犁体功率消耗的增长变化情况，如图13和图14所示。

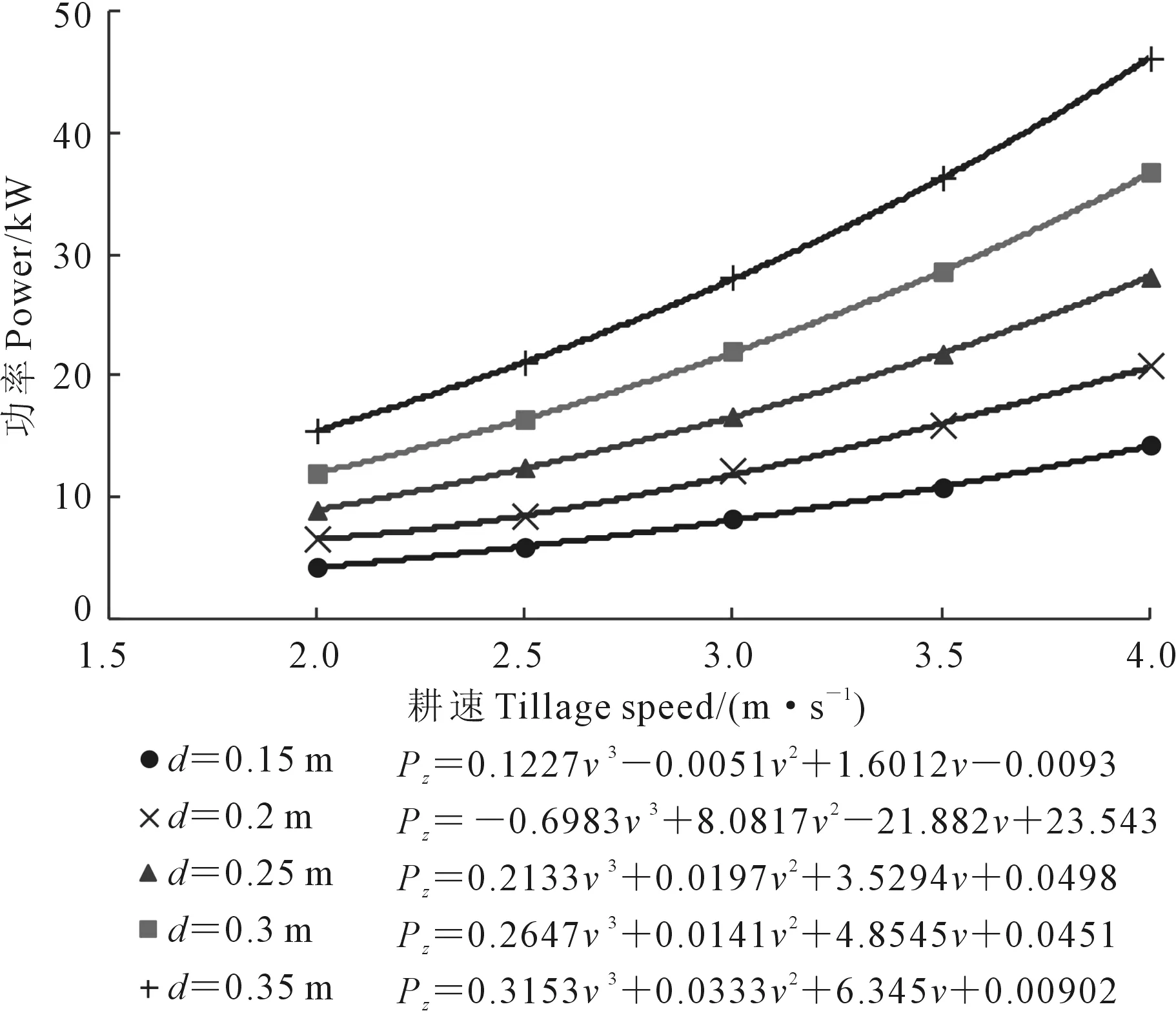
图13 犁体A功率消耗随耕速变化关系Fig.13 Relationship between plough A power consumption and speed

按照当前西北玉米地犁耕作业要求，耕深一般在0.3 m左右，此时功率消耗主要与耕作速度变化有关，在高速犁耕作业情况下，速度为3.5 m·s-1时，犁体A功率消耗28.6 kW，犁体B功率消耗34.8 kW。

当犁具配置N铧犁体时，犁具需要最小配套动力(P)：

P=N(q1v3+q2v2+q3v)

(23)

两台分别配置犁体A和犁体B的5铧犁，按照上述作业条件，至少需要143 kW和174 kW配套动力。

同时，可以根据上述分析，依据犁体结构、土壤参数和犁耕作业等参数，设置合理的安全系数(sf)，优化选配合适的匹配动力，促进犁具与拖拉机功率(Ps)的优化匹配，避免造成能耗的浪费，优化农机动力资源合理利用。

Ps=sfP

(24)

关于此处的安全系数(sf)的选取还有待于进一步试验研究。

3.2.7 犁体耕作性能分析 测量了两种犁体在玉米地的作业性能指标，如表6所示，两种犁体的作业性能基本一致。根据试验可以看出，随着作业速度的增加，耕作阻力在不断增加，相应的土垡破碎率和植被覆盖率都有所提升，而耕深和耕宽稳定性有一定的下降，但都在合理范围之类。

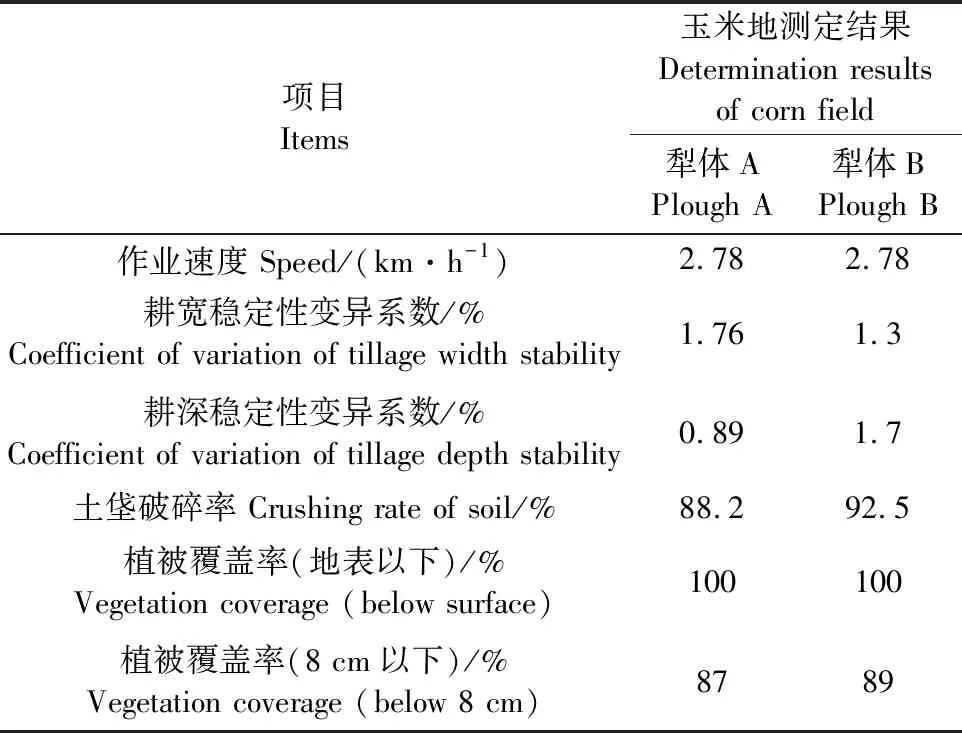
表6 犁体耕作性能Table 6 Plough performance

4 结 论

1)建立了基于摩尔-库仑土壤剪切理论的犁体耕作阻力模型，模型包含了犁体结构参数、土壤物理特性和犁体工作参数等，基于新疆玉米地土壤物理特性，并根据前期试验筛选出在该类型土壤中耕地作业适应性较好的两种高速犁体A和B，建立了耕作阻力方程，预测计算了在不同耕宽、耕深和耕速作业条件下对应的耕作阻力。在不同的耕深、耕宽和耕速条件下进行仿真分析，得出对应的仿真值。根据犁体A与犁体B的耕作阻力计算与仿真分析对比，其中，犁体A仿真值与计算值的平均误差为3.37%，最大误差为5.1%，犁体B仿真值与计算值的平均误差为4.23%，最大误差为5.6%。

2)对犁体A和B进行了田间耕作阻力试验，试验测试了在不同耕宽、耕深和耕速条件下的耕作阻力，并与仿真分析、理论计算结果进行比较，犁体A试验值与计算值的平均误差为7.18%，最大误差为10.8%，试验值与仿真值的平均误差为3.71%，最大误差为9.4%。犁体B试验值与计算值的平均误差为7.92%，最大误差为13.8%，试验值与仿真值的平均误差为3.55%，最大误差为9.9%。由此可以看出，理论计算、仿真分析均接近试验值，误差在合理范围，从而验证了理论模型和离散元仿真模型预测分析犁体耕作阻力是可行的。

3)总结分析了犁体结构参数对耕作阻力的关系，为设计低阻犁体提供了参考。分析了犁体耕作阻力与耕宽、耕深、耕速的关系，犁体耕作阻力随着耕宽的增大呈非线性增长关系，而耕宽的变化主要取决于铧刃与运动方向夹角的大小。犁体耕作阻力与耕深呈三次函数增长关系，与耕速的呈二次函数关系。预测了犁体A和犁体B在耕作深度0.15、0.2、0.25、0.3、0.35 m下，耕作速度在2、2.5、3、3.5、4 m·s-1时犁体耕作过程的阻力值，绘制了对应的预测曲线图，给出了对应的方程，为犁体结构降阻设计提供了方向。

4)根据犁体耕作阻力模型，分析了犁体耕作过程的功率消耗，犁体耕作过程的功率消耗与耕速呈三次函数的增长关系，理论分析了在不同耕宽、耕深和耕速条件下的功率消耗值，绘制了功率变化曲线图，并推导出对应的方程。进而分析了配置有多铧犁体的情况下，所对应需要合理配置的配套动力，设置合理的安全系数，优化选配合适的匹配动力，促进犁具与拖拉机型号的优化匹配。