基坑钢支撑应变的温度效应消除算法
2022-01-27刘小强王立新
王 超,刘小强,王立新
(1.长安大学信息工程学院,陕西西安 710064;2.中铁第一勘察设计院集团有限公司,陕西西安 710043)
在基坑工程中,温度是钢支撑应变变化的重要影响因素[1-2],且温度与钢梁应力之间满足线性关系[3],温度影响会使结构自身引起的应变信息被掩盖,降低监测系统的准确率,不利于监控系统对工程安全状态的评估。但关于消除温度影响的研究较少。文献[4]在利用光纤应变计监测结构柱体弯矩的过程中,基于温度场对于柱体两侧应变计影响一致的原理,通过将两侧监测的应变量相减,抵消了应变温度效应,但并没有得出消除温度效应的应变量。近几年对应变温度效应的研究主要针对桥梁结构。但一些研究方案[5-8]适用于分离桥梁结构动荷载引起的高频应变与温度引起的主体趋势应变,而一般情况下,基坑钢支撑结构应变变化相对桥梁结构更平缓,动荷载高频分量很低,应变主体趋势的影响因素除温度外也有基坑结构自身的因素,故不能用这类方案直接处理基坑钢支撑结构的应变监测数据。文献[9]、文献[10]通过对比温度小波分量、应变小波分量变化趋势的相关性来确定温度引起的应变量。这类方案相对有效,但缺乏客观性依据,一方面没有相关性数据分析,另一方面不能因为其他分量趋势相关性低就认为该应变分量与温度无关。
针对基坑环境下钢支撑应变的温度效应,提出一种基于数据融合与小波分解的温度效应消除算法。利用小波分解算法及相关系数分析提取有效的温度应变分量,构建温度-应变回归模型,求出温度引起的应变量,达到消除温度效应的目的。同时为了得到有效的监测数据,引入了数据融合技术,在卡尔曼滤波融合算法上进行改进,在保证去噪性能的基础上,保留异常监测值。
1 算法分析及实现
算法分为3 步:1)基于多传感器融合数据精度高于单传感器测量精度的原理,利用改进的卡尔曼滤波融合算法对多组应变数据、温度数据分别进行组间融合。2)对融合后的应变、温度数据进行小波分解,分析两种数据相同分量之间的相关性,通过时域段截取或重复小波分解从各分量段挖掘、提取由温度造成的应变分量,对各分量进行重构。3)通过二次光滑局部线性回归法建立温度与应变的回归模型,掌握温度与应变的定性关系,达到消除温度效应的目的。
1.1 改进的卡尔曼滤波融合算法
卡尔曼滤波融合算法基本原理是先对单源传感器数据进行卡尔曼滤波估计,然后将最优估计值进行融合[11]。卡尔曼滤波融合算法相对于其他自适应加权融合算法[12-13]的特点在于可以滤去数据的毛刺噪声,提高监测数据的可信度。融合方式如下:
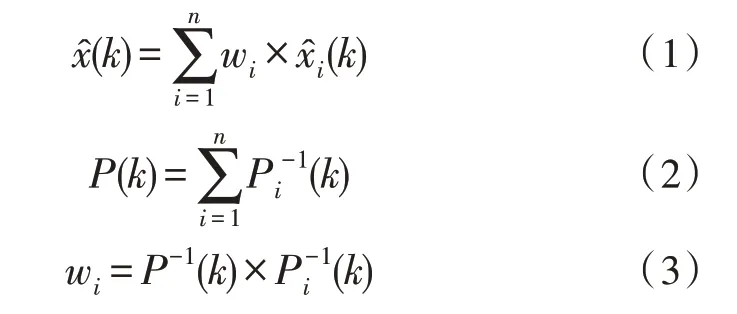
表示k时刻下第i个传感器监测值的卡尔曼滤波最优估计量,i=1,2,3,…,n,wi表示每一个最优估计量对应的加权值,由在k时刻下对应的估计误差协方差Pi(k)计算得出,为k时刻下多源传感器监测值的融合结果。
当前卡尔曼滤波融合算法的改进主要针对于消除误差、消除异常值[14-15]。但是若被监测对象状态发生异常变化,各组监测数据会产生突发峰值。此时的异常峰值也属于被测对象真实的状态变化情况,卡尔曼滤波算法往往将产生的峰值滤去,不能反映被测对象真实的变化状态。针对该情况,对卡尔曼滤波融合算法进行改进。
由被测对象本身引起的异常数据有两个特征,一是监测数据值变化远高于其他时刻数据,二是由于引起多组传感器监测数据发生异常的原因一致,都是由被测对象本身状态异常引起的,且该异常因素对数据的变化起决定性作用,同时刻下多组监测数据差异相对于数据整体变化量很低。
通过计算同时刻下多组监测数据的标准差,判定数据间差异的大小,差异低标准差趋向或等于0,而标准差倒数值会很高,相对于其他受噪声干扰的同时刻数据标准差,倒数值呈现异常状态(在实际监测中噪声是广泛分布),改进的卡尔曼滤波融合算法的基本步骤如下:
1)n组传感器在一个时域段的监测数据Z1,Z2,Z3,…,Zn,每组数据包含m个时刻的值,通过卡尔曼滤波融合算法融合,得到融合结果。
2)将各组数据Z1,Z2,Z3,…,Zn分别与相减,得到每组传感器数据相对于融合结果的相差量ΔZ1,ΔZ2,ΔZ3,…,ΔZn。
3)求ΔZ1,ΔZ2,ΔZ3,…,ΔZn在t时刻的监测数据ΔZ1(t),ΔZ2(t),ΔZ3(t),…,ΔZn(t) 的标准差σ(t)、平均值m(t),若此时标准差为0,则该时刻融合结果转至步骤5),且该时刻监测数据不计入步骤4)的判断序列当中。
4)平均值序列为α=[m(t1),m(t2),m(t3),...,m(tm)],标准差倒数序列为θ=[σ-1(t1),σ-1(t2),σ-1(t3),..,σ-1(tm)]。将两个序列中每一个对应值相乘得γ=[σ-1(t1)m(t1),σ-1(t2)m(t2),...,σ-1(tm)m(tm)],用拉依达准则(3σ2准则)判别序列γ中的异常点。
5)若γ(tk)数据异常,则认为tk时刻传感器监测数据无差异、数据整体异常,不能用滤波算法剔除,其融合结果用同一时刻多组数据加权系数融合值[12]替代。
1.2 小波分量相关性分析
先对钢梁同一区域按一定间隔布置多个应变传感器,每个传感器可以采集温度数据,然后对采集得到的应变数据、温度数据进行数据融合。Zε、ZT是对应变数据、温度数据分别进行融合得到的融合结果,通过小波分解算法将应变、温度数据分解为不同频段的分量,可采用Symlets 小波作为基小波,小波阶数为8,小波阶数与基小波可根据实际数据监测情况调整,分别对温度融合数据、应变融合数据进行4层分解,结果如图1 所示。
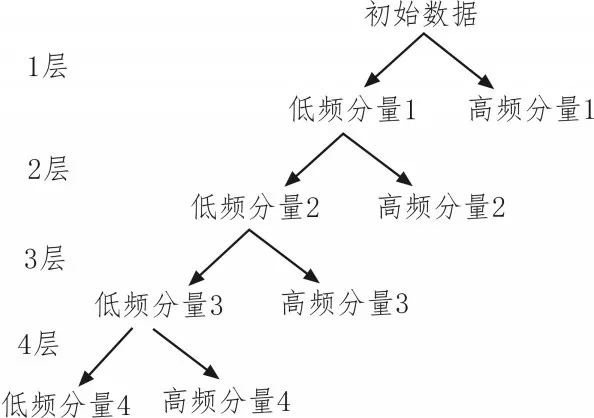
图1 小波分解图
Zε、ZT经小波分解算法得到ε1、ε2、ε3、ε4、εd与T1、T2、T3、T4、Td两组分量,对应于高频分量1、高频分量2、高频分量3、高频分量4、低频分量。通过温度、应变数据同频段分量的相关性分析来提取温度引起的应变分量。
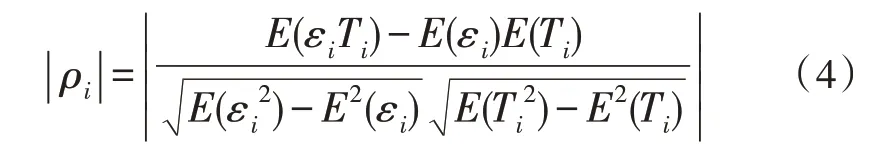
|ρi|表示同频分量εi、Ti之间的相关性系数,其中i=1,2,3,4,d。|ρi|位于0 到1 之间,越接近1,表示两组数据相关性质越高,以0.5、0.75 为两个相关性判断阈值,分析步骤如下:
若0.75 ≤ |ρ|,认为该频段应变分量中主要是由温度引起的。
若0.5 ≤ |ρ|<0.75,则认为该频段上的应变分量与温度有关,但是在某些时域段也存在较高的结构自身因素引起应的变量,掩盖了该时域段温度对应变的影响信息,使得该频段分量相关性降低。
该情况有两种处理方式,一种是主观分析,0.5 ≤ |ρ|时,一般两种数据的相关趋势已经很明显,通过时域上应变、温度相同频段分量的变化趋势对比,截取相关性较高的数据段作相关系数检测,若相关系数满足0.75 ≤ ||ρ,则认为这一段应变数据是由温度引起的,但若采集的数据段过短,无法保证回归模型的准确性,则该方式不可取;另一种是对这一频段的温度、应变分量进一步作小波分解,继续对同频分量进行相关性分析,提取温度应变分量。
1.3 构建回归模型消除温度效应
二次光滑局部线性回归算法是建立于局部回归基础上的非参数回归方法[16]。算法分为两步,第一步是基于最小化加权平方和的核函数局部回归,得到一次回归估计值;第二步在一次回归的基础上根据带宽对回归模型的一次估计值进行积分光滑拟合。

1)求η(T)对应的一次核回归模型估计值与一次核回归模型一阶导数η′(T)的估计值。方法如下:

2)对估计量进行二次光滑回归,方法如下:
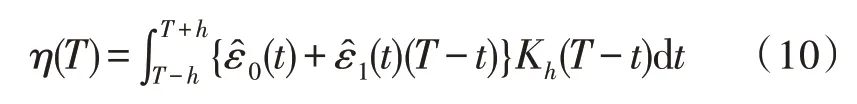
式中,Kh(T)表示核函数,核函数阶次越高,拟合结果偏差越小,但运算量越大。h为回归带宽长度,带宽选取要结合实际数据分析,过长或过短都会降低回归模型的准确性,基坑应变监测数据中带宽选取0.5 到1 之间数值。求得回归模型后,利用回归模型通过已有的温度监测数据ZT,计算整个时间段下温度引起的应变量,则结构自身应变量为。
2 实验分析
2.1 实验模型
实验数据采用某地铁基坑工程中横向支撑钢梁的应变、温度监测数据,基坑支护形式采用排桩-内支撑形式,总长为364.9 m,宽25 m,深18 m。
图2 是基坑横向支撑钢梁上振弦应变传感器布置示意图,A1、A2、A3、A4 表示同一支撑钢梁上的4个应变测试点,A1、A3 与A2、A4 分别布置在钢梁中央区域两侧,每个测试点布置了应变传感器与温度传感器,数据测试时间为2019 年3 月1 日到3 月26日,采样间隔为60 min,各个传感器采样时间同步。
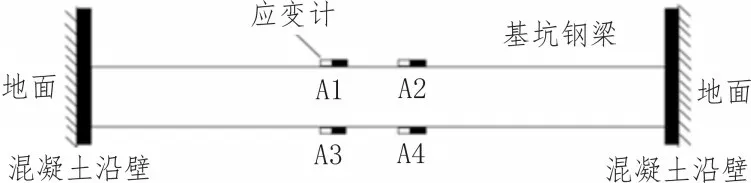
图2 支撑钢梁俯视图
2.2 改进的数据融合算法
2.2.1 温度、应变融合数据相关性分析
对各个测点的温度与应变数据之间、两种数据的融合结果之间进行线性拟合,利用F检验法则[17]对各个拟合关系式进行线性关系检验,检验结果如表1所示。

表1 各测点线性关系分析
表1 中,α表示显著水平,F1表示检验统计量的临界值,检验统计量F越高,温度、应变数据的线性关系越显著,若低于F1,则拒绝拟合关系。通过分析发现,温度与应变数据总体呈线性关系,但Z2 测试点没有通过线性关系检验,由于4 个测试点的布置位置相近,温度、应变变化状态也应该相似。影响因素是传感器本身或者数据传输过程中受到的异常影响。温度、应变融合结果线性关系显著,有效排除单源数据受到的干扰因素,反映出钢梁温度、应变状态的变化趋势,为进一步分析提供有效的数据支撑。
2.2.2 数据融合算法对比
选取A1 点监测应变数据,在第250~252,305~307 数据点插入了16 με 异常值,假设这是被测对象在这两个时间段状态发生异常而呈现出来的异常值。对其随机加噪,得到4组加噪后的仿真数据A11、A12、A13、A14,然后在几组加噪数据中随机插入16 με异常值,认为异常值是由于传感器随机受到的干扰造成的。假设这4 组数据是4 个同质传感器监测同一对象得到的数据,加入异常值的A1 点监测数据为4 组仿真数据的真实值,利用加权系数融合算法、卡尔曼滤波融合算法、改进卡尔曼滤波融合算法分别进行融合,对比真实监测数据。结果如图3 所示。
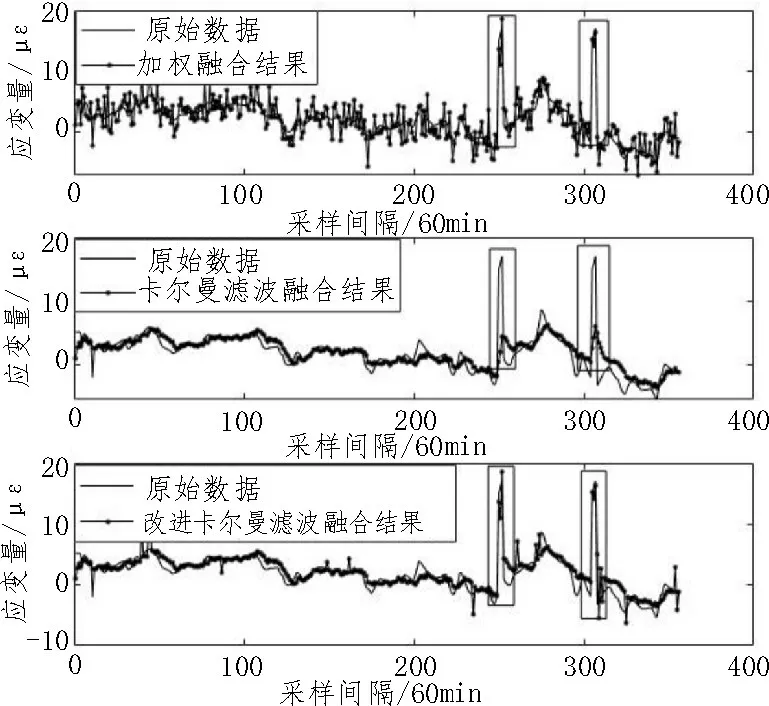
图3 融合算法对比
在不计入添加异常值的情况下,加权融合结果、卡尔曼滤波融合结果、改进的卡尔曼滤波融合结果标准差为5.4、4.7、4.9。结合图中信息,对于加噪后随机插入的异常值,都被3 种融合算法滤除了。对于每组数据在第250~252,305~307 数据点都插入了异常值,加权融合结果虽然保留了异常值,但是同时保留了大量毛刺噪声,标准差最高。而卡尔曼滤波融合结果滤掉了大量毛刺噪声,在正常情况下融合结果与真实数据贴近,但是滤去了异常变化值。改进的卡尔曼滤波融合算法不仅滤去了噪声,标准差与改进前的融合结果相近,且保留了异常峰值。
2.3 钢支撑应变温度效应消除
2.3.1 实测数据处理
对融合后的应变数据进行处理,得到基坑结构自身应变及温度引起的应变,如图4 所示。经计算,这一段时间温度引起的应变量平均值与标准差分别为-7.5 με、5.0,结构自身应变量平均值与标准差分别为1.1 με、2.5,温度引起的应变量与结构自身应变量平均比值约为7∶1。温度引起的应变量变化波动幅度较高,整体应变向下变化,变化范围约为0~-20 με。基坑结构自身对钢梁应变的影响较低,变化范围约为-2~8 με,基本围绕0 με 波动,幅度较低,变化较为平稳,说明这段时间内基坑结构对于钢梁状态影响很稳定,与实际数据采集现场情况相符。
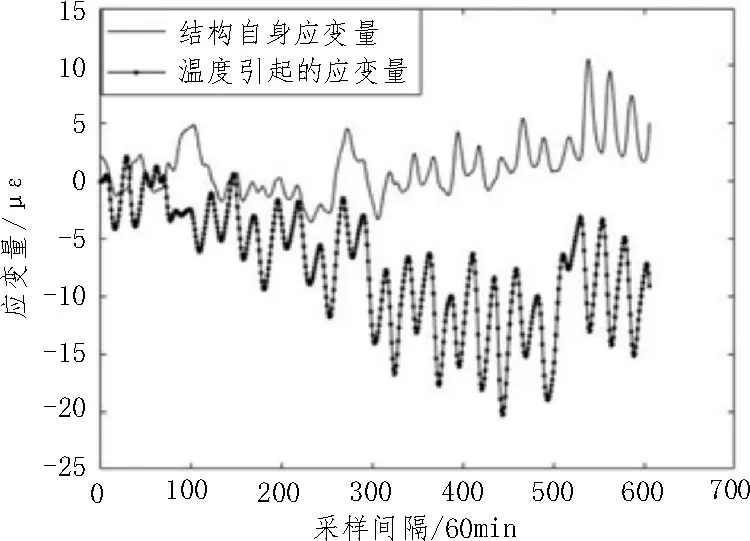
图4 温度引起的应变量与结构自身应变量
2.3.2 算法仿真对比
局部加权回归法[9]定义为算法1,多元回归算法定义为算法2,由于样本数据采样间隔为60 min,只考虑前一时刻、当前时刻温度对应变的影响,构建二元回归模型,小波分量分析[10]定义为算法3,文中提出的温度效应消除算法定义为算法4。假设温度T、应变ε满足线性关系:ε=-1.684T+6.053(A4 测点的温度、应变数据近似满足该线性关系式),利用A1点监测的温度数据通过该关系式得到应变量数据εT;随机生成标准差约为2.5 的应变数据,假设是由结构自身引起的应变量εF;将两者叠加得到总应变量εs。分别利用上述算法从εs中提取温度引起的应变量,对比不同算法下εT、之间的均方根误差值(Root Mean Square Error,RMSE)。
图5中,经10次仿真实验,算法1、算法2、算法3、算法4 平均误差分别为3.23、1.17、3.44、0.98,算法4的误差比其他3 种算法依次平均每次降低了69%、16%、71%。算法2 RMSE 值相对算法4 平均高出0.19,但差异不如其他两种算法明显,这是因为构建的随机序列波动幅度较低,且分布均匀,总体应变的变化趋势由温度决定,假若结构自身应变在某段时域产生了较高幅度的应变变化,影响了应变总体变化趋势,如图6所示。在这种情况下,分别通过算法3与算法4 提取温度应变量,计算与初始温度应变量εT之间的RMSE 值。经5 次仿真实验,每次产生的结构自身应变不同,算法4 比算法2 误差平均每次降低了0.68,是之前0.19 的3.58 倍,算法2 误差更高。
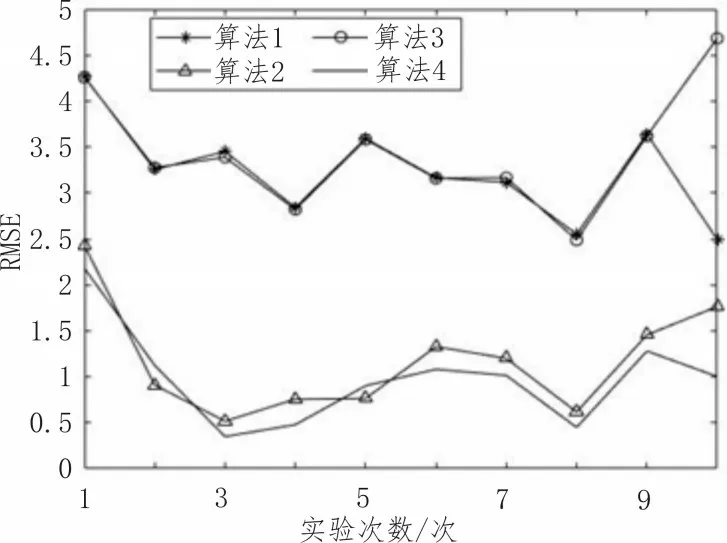
图5 算法对比
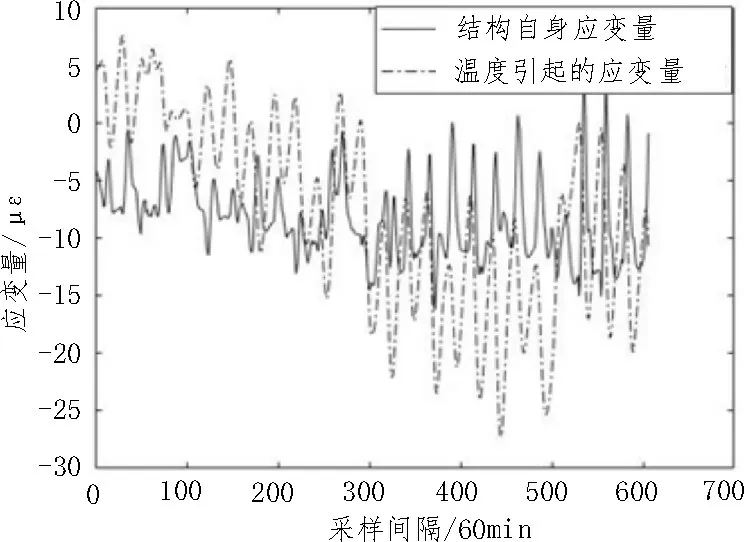
图6 结构应变过高趋势对比
3 结论
1)对于基坑钢支撑应变数据,提出的温度效应消除算法相对于已有的几种针对桥梁结构应变的温度效应消除算法,提取出的温度应变分量与真实值之间的RMSE 值更低,更接近于真实值,得到的结构自身应变量更准确。
2)改进的卡尔曼滤波融合算法可有效剔除数据噪声干扰,且保留被测结构自身因素引起的异常值,提高了监测数据的准确性。但不足之处是改进卡尔曼滤波算法的抗噪性能比改进前低,需要进一步完善。
3)在基坑环境中,正常状态下温度引起的钢支撑应变量很高,基坑结构自身导致的应变量较低、趋势较为平缓,温度与应变量之间满足线性关系。
