基于随机森林算法与高分观测的太湖叶绿素a浓度估算模型*
2022-01-27杭蓉蓉孙良宵朱士华
杭 鑫 曹 云 杭蓉蓉 徐 萌 霍 焱 孙良宵 朱士华
1 江苏省气候中心,南京 210019
2 中国人民解放军61175部队,南京 210049
3 上海翔竑信息技术有限公司,上海 202172
4 江苏省常州市气象局,常州 213000
提 要: 基于2018年和2019年有效观测的高分1号(GF-1)卫星影像和湖面原位观测的叶绿素a浓度数据,利用随机森林算法定量评价特征变量重要性的功能,选择有效特征波段组合,建立了基于原位自动监测数据的太湖叶绿素a浓度的遥感反演模型。结果表明:绿光波段(0.52~0.59 μm)和红光波段(0.63~0.69 μm)是遥感估算叶绿素a浓度的关键波段,与其他波段组合可以定量估算叶绿素a浓度;分季节构建太湖叶绿素a浓度估算模型效果更好,春、夏、秋、冬各季模型的决定系数R2分别达0.84、0.85、0.96和0.82;太湖叶绿素a浓度夏季最高,秋、春季次之,冬季最低;春、秋和夏季叶绿素a浓度空间变化较明显,而冬季变化不明显,叶绿素a浓度高值区主要集中在西部沿岸区、竺山湖、梅梁湖和部分湖心区。研究表明:随机森林模型可以客观确定遥感反演叶绿素a浓度的有效波段,实现大面积内陆水体叶绿素a浓度的高精度估算。
引 言
叶绿素a是浮游植物或藻类植物中最丰富的色素,准确定量估算叶绿素a浓度对于客观评价水体富营养化程度、实施水环境治理和生态保护具有重要意义(朱广伟等,2018;尹艳娥等,2014)。太湖是一个典型的内陆Ⅱ类水体,水质状况存在明显的空间异质性(水利部太湖流域管理局,2019)。传统的叶绿素a浓度测量方法主要是人工采样监测,在实验室采用分光光度法进行分析,最快也要近一天时间才能获取结果,无法满足政府防控需求。2008年以来采用了浮标站自动监测水质参数,这是一种基于荧光法的半定量分析方法,可在半小时内获得结果,其精密性和时效性都较高(刘苑等,2010)。但传统方法缺乏时空连续性,观测站点有限,观测数据可能有缺失,难以准确描述复杂水体的叶绿素a浓度与光谱特征之间的关系(王桥等,2008)。卫星遥感技术具有监测范围广、时效快和连续动态等优势(张鹏等,2018),越来越多地应用于大面积水体叶绿素a浓度估算(He et al, 2020;赵少华等,2019)。遥感反演叶绿素a浓度的方法大体可分为经验统计方法(Zhang et al, 2014)、半经验半分析方法和分析模型(张明慧等,2018)。经验方法主要通过建立水体反射率与实测叶绿素a浓度之间的定量关系来估算叶绿素a浓度,半经验半分析方法则是在经验方程的基础上结合辐射传输模型,有一定的物理基础。由于叶绿素a光学特征复杂和图像的大气校正不精确,光谱特征与组分浓度之间的关系较为复杂,经验、半经验模型较难解决复杂的非线性问题,反演精度可能较差(张玉超等, 2009b),而分析模型虽具有较高的反演精度和较好的通用性(韩留生等,2014),但机理复杂,建模难度大,实用性较差(潘应阳等,2017)。总体而言,精确遥感反演浑浊水体叶绿素a浓度仍是当前较为困难的任务(Nazeer and Nichol, 2016)。
随着人工智能技术的发展,机器学习算法开始在水质参数遥感反演中得到应用。由于机器学习方法不依赖于固定的模型框架,而是通过不断地“学习”模型校正过程中反馈的误差,来完善自变量与因变量之间的复杂关系,因而是解决非线性回归问题的有效方法(Lary et al, 2016;孙全德等,2019)。已有研究证实BP神经网络(BP neural network)模型在遥感反演太湖叶绿素a浓度时是可行的(朱云芳等,2017),但神经网络模型需要确定网络结构,参数较多,且随着训练样本的增加,所构建的最优网络可能是局部最优,会出现“过学习”的现象。支持向量机(support vector machine,SVM)模型在反演叶绿素a 浓度时也获取了较高的精度(Kong et al, 2017),且与BP模型相比,SVM模型的反演精度可能更高,稳定性、鲁棒性和空间泛化能力也可能更好,但对于大规模训练样本的SVM模型可能会耗费大量的机器内存和运行时间,导致学习效率降低(张玉超等,2009a)。Breiman提出的随机森林模型是一种组合分类智能算法,具有极高的准确率、极强的数据挖掘能力及分析复杂相互作用分类特征的能力等很多优点,并且可以给出变量重要性估计,甚至被誉为当前最好的机器学习算法之一(Breiman, 2001;李文娟等,2018;刘扬和王维国,2020;王可心等,2021)。近年来已有一些学者尝试利用随机森林机器学习算法开展近岸水色遥感监测,但在浑浊水体定量估算叶绿素a浓度的研究仍相对较少,其中叶绿素a 浓度实测数据也大多采用人工定点采样实验室分析而来,自动监测数据的应用较为少见,而水质参数自动监测应是今后的必然趋势,因此,有必要充分利用好水质自动观测数据,提高叶绿素a 浓度定量估算精度。
本文利用2018年和2019年有效观测的GF-1影像和同步自动观测的叶绿素a浓度数据,采用随机森林机器学习算法,选择有效特征波段组合,建立太湖叶绿素a浓度的遥感估算模型,了解太湖水体叶绿素a浓度时空分布特征,试图为蓝藻水华发生发展预测预警提供重要参数,为蓝藻水华防控提供科学依据。
1 数据和方法
1.1 研究区域
选取太湖作为研究区,其地理范围在30°55′~31°30′N、119°55′~120°40′E;湖面面积约为2 338 km2,平均水深约为2 m。
1.2 遥感数据
选取GF-1卫星搭载的Wide-Field-of-View(WFV)传感器观测得到的卫星影像作为遥感数据源,所有数据均来自于高分辨率对地观测系统江苏数据与应用中心,时间范围为2018年1月至2019年5月。选择有蓝藻水华发生、晴朗或少云天气时质量较高的影像,最后共获得18天27景影像,日期分别为,2018年:1月12日,2月5日,2月6日,2月13日,2月23日,4月8日,4月28日,5月15日,5月23日,6月25日,7月19日,7月20日,10月6日,10月27日,12月18日;2019年:1月17日,1月24日,5月3日。
由于原始影像为1级(相对辐射校正产品),为准确获得水体表面反射率,需对数据进行正射校正、辐射定标、大气校正和影像镶嵌等预处理。
1.3 叶绿素a浓度实测数据
叶绿素a浓度数据取自江苏省生态环境厅布设在太湖的19个水质浮标站自动监测数据,站点分布如图1。由于卫星影像过境时间为每日11:30(北京时,下同)左右,因此实测数据选取与卫星观测相同日期每日11:30的瞬时观测值。

图1 水质浮标站点分布Fig.1 Distribution of water quality buoy sites
1.4 随机森林基本原理
随机森林算法基本思路是:(1)首先确定原始总样本集D和变量个数M;(2)基于原始训练样本集D,采用重采样技术从中抽取N个决策树数目Ntree(number of trees)与D中样本数量相同的子训练样本集D1,D2,D3,…,Dn,分别建立Ntree个回归树模型,未抽取的部分组成袋外数据(OOB)作为测试样本;(3)确定树节点预选变量个数Mtry(number of variable per level)的数值,Mtry代表在决策树节点做决定时所用变量数,一般Mtry须小于等于原始数据变量个数M;(4)针对每个训练集生长一棵分类回归树,按照节点不纯度最小原则在树的每个节点处,依据法则在Mtry个特征变量中选择高分类能力的特征进行分支生长,并且每棵树都不做任何裁剪,任其最大限度的生长;(5)重复步骤(4)n次,得到由n棵决策树组成的随机森林;(6)随机森林的最终回归结果为每棵树结果的平均值,预测精度则以每棵回归树的平均OOB误差来确定。
随机森林模型精度取决于Ntree和Mtry。Ntree决定了随机森林的总体规模,Mtry决定了单棵决策树的生长状况,两者分别从宏观和微观层面决定随机森林的精度。在回归模型中,Mtry值通常为变量数的三分之一,Ntree值根据模型误差随决策树数目变化情况来决定。
随机森林模型支持定量化比较各自变量之间对于模型的重要程度,在建模时,可以从大量特征变量中选取对最终结果影响较大的数目较少的特征变量,删除一些和任务无关或者冗余的特征变量,简化的特征数据集也常常会得到更精确的模型。变量重要性度量的主要评价指标为精度平均减少值IncMSE (increasing the mean square error)和节点不纯度减少值IncNodePurity (increasing the node impurity),值越大,表明该变量越重要,反之则相对不重要。
2 结果与分析
2.1 样本处理与潜在变量分析
从所有18天GF-1卫星过境时刻的实测叶绿素a浓度数据中,剔除缺测、异常值及受云影响的152个数据,最终得到190个数据组成了实测叶绿素a浓度样本数据集。再根据不同季节分组,分别得到春季(3—5月)57个,夏季(6—8月)30个,秋季(9—11月)20个和冬季(12—2月)83个实测叶绿素a浓度的样本子集。从各样本子集中随机选取四分之三的数据作为训练样本集,剩下四分之一数据作为测试样本集。
基于随机森林模型的叶绿素a浓度遥感估算模型是以GF-1 WFV影像为主要数据源。采用GF-1 WFV 4个波段的反射率进行水质参数反演有其合理性,但单一波段往往不能很好地反映影响因子与水质参数之间的关系(朱云芳等,2017)。参考方馨蕊等(2019),将GF-1 WFV 4个波段及不同组合的39个变量因子作为潜在变量进行筛选(表1)。

表1 参与随机森林建模的39个潜在变量因子Table 1 39 latent variable factors involved in random forest modeling
2.2 关键波段变量因子确定
首先,确定随机森林回归模型中最重要的两个输入参数Mtry和Ntree。Mtry取潜在变量总数39的三分之一,即Mtry=13,而Ntree值根据误差分析来确定。由于参数Mtry值固定不变,那么参数Ntree值越大,则误差Error越小或趋于稳定,代表模型精度越高。为考察不同季节叶绿素a浓度反演的情况,分别建立了全部样本模型(MODAll)、春季模型(MODSpr)、夏季模型(MODSum)、秋季模型(MODAut)和冬季模型(MODWin)共5个模型。5个模型在不同的Ntree和Mtry组合下所对应的分类精度如图2所示。由图看出,MODAll和MODSpr的误差在Ntree为600时趋于稳定,MODSum的误差在Ntree为500时趋于稳定,MODAut的误差在Ntree为200时趋于稳定,MODWin的误差在Ntree为400时趋于稳定。综上所述,我们确定在MODAll和MODSpr中,Ntree=600;在MODSum中,Ntree=500;在MODAut中,Ntree=200;在MODWin中,Ntree=400。

图2 决策树数目Ntree与模型误差的关系(a)MODAll,(b)MODSpr,(c)MODSum,(d)MODAut,(e)MODWinFig.2 The relationship between decision tree Ntree and model error(a) MODAll, (b) MODSpr, (c) MODSum, (d) MODAut, (e) MODWin
然后,分别根据单一指标IncMSE和IncNodePurity筛选波段因子变量。随机森林回归模型通过评估每个变量对总体模型预测精度提高的能力,对这些变量进行排序,评估各变量在模型中的相对重要性。利用上述方法确定的参数Mtry和Ntree分别进行建模和模型优化,MODAll、MODSpr、MODSum、MODAut和MODWin模型各单独训练5 000次,从中各选择精度相对较高(相关系数R>0.85)的20个模型,对应每个变量都可以得到20个IncMSE和IncNodePurity值。分别计算每个变量的IncMSE和IncNodePurity指标的平均值,然后根据这两个指标平均值的大小分别进行排序。将指标平均值排名相对靠前且重要性度量曲线出现较明显拐点前的特征变量认为是相对重要的变量,由此得到全部样本模型MODAll、春季模型MODSpr、夏季模型MODSum、秋季模型MODAut和冬季模型MODWin共5个模型的单指标重要变量筛选结果:
(1) 基于IncMSE指标的筛选结果
MODAll:DVI(2, 3),VI(2,1,3),RVI(2, 3),NDVI(2, 3),VI(2,1,3,4),VI(2,3,4),DVI(2, 4),VI(2,1,4),B1,VI(3,1,2);
MODSpr:VI(2,1,4),DVI(2, 3),VI(2,1,3),VI(2,1,3,4),DVI(1, 2);
MODSum:VI(3,1,2),RVI(1, 3),DVI(2, 3),RVI(2, 3),DVI(1, 3);
MODAut:VI(2,3,4),RVI(1, 2),VI(1,2,3,4),VI(1,2,3),VI(4,1,2),NDVI(2, 4),VI(1,2,4),VI(1,3,4),DVI(1, 2);
MODWin:RVI(2, 3),RVI(2, 4),VI(2,1,3,4),VI(2,3,4)。
(2) 基于IncNodePurity指标的筛选结果
MODAll:VI(2,1,3,4),VI(2,3,4),VI(2,1,3),B4,VI(2,1,4),DVI(2, 3);
MODSpr:VI(4,1,3),NDVI(1, 4),VI(4,1,2,3),EVI;
MODSum:RVI(1, 3),VI(3,1,2),VI(2,3,4),VI(1,3,4);
MODAut:VI(2,1,3),RVI(2, 3),DVI(1, 2),VI(4,1,2,3),VI(4,1,2),DVI(2, 3),VI(4,2,3),B4,NDVI(2, 3),EVI;
MODWin:RVI(2, 3),VI(2,3,4),VI(3,1,2),RVI(2, 4)。
从上述两类筛选结果中,发现同时包含B2和B3波段变量因子出现次数较多,在IncMSE指标的筛选结果中出现19次,占比为58%,在IncNodePurity指标的筛选结果中出现16次,占比为57%;而包含B2或B3波段变量因子出现次数更多,在IncMSE指标筛选结果中共出现32次,占比为97%,仅1个变量因子不包含B2或B3波段,在IncNodePurity指标筛选结果中累计出现25次,占比为89%,仅3个变量因子不包含B2或B3波段,说明B2和B3波段在所有变量因子中占主导地位。
最后,根据结合IncMSE和IncNodePurity的综合因子筛选关键波段因子。已有文献在筛选特征变量因子时,大多选择IncMSE和IncNodePurity中的一种指标(罗晓春等,2019)。但从以上两种指标的筛选结果中可以发现,同一种模型不同指标筛选出的变量因子并不完全相同。相对应于这两个指标,所有模型经过筛选得到两组不同的变量因子。对于MODAll,单用指标IncMSE筛选得到10个变量,用指标IncNodePurity得到6个变量,两组变量中出现5个相同因子。相类似的,MODWin有3个相同因子,MODSum中有2个相同因子,MODAut中仅有1个相同因子。我们注意到模型MODSpr的两组筛选结果中甚至没有出现相同的变量因子。表明仅用IncMSE或IncNodePurity一个指标并不能完全反映变量的重要性,存在一定的局限性。为此,考虑综合IncMSE和IncNodePurity两种指标构建一组新的变量相对重要性评价指标(relative importance evaluation index,RIEI),具体计算方法是:对于MODAll、MODSpr、MODSum、MODAut和MODWin这5个模型中的每个模型,首先分别将以上20个模型的IncMSE值和IncNodePurity值进行归一化处理,然后再求平均值,得到每一个变量的RIEI值:
(1)
式中:IncMSEi为第i个IncMSE值,IncMSEmin为20个IncMSE中的最小值,IncMSEmax为20个IncMSE中的最大值;IncNodePurityi为第i个IncNodePurity值,IncNodePuritymin为20个IncNodePurity中的最小值,IncNodePuritymax为20个IncNodePurity中的最大值。
将包含全部样本和春、夏、秋和冬季共5个模型的RIEI值绘制成变量重要性评估曲线(图3)。

图3 基于RIEI值的5个模型的变量重要性评估曲线(a)MODAll,(b)MODSpr,(c)MODSum,(d)MODAut,(e)MODWinFig.3 Variable importance evaluation curve of five models based on RIEI value(a) MODAll, (b) MODSpr, (c) MODSum, (d) MODAut, (e) MODWin
将变量重要性排名相对靠前且曲线出现较明显拐点前的特征变量认为是相对重要的变量,分别筛选出5个模型的重要特征变量:
MODAll:VI(2,1,3,4),VI(2,3,4),VI(2,1,3),B4,VI(2,1,4),DVI(2, 3),NDVI(2, 3);
MODSpr:DVI(1, 2),VI(2,1,4),VI(2,1,3,4),RVI(1, 2),VI(2,1,3),DVI(2, 3),VI(1,2,3);
MODSum:RVI(1, 3),VI(3,1,2),RVI(2, 3),VI(2,3,4),VI(1,3,4)、DVI(2, 3),DVI(1, 3),VI(1,2,3,4),VI(2,1,3,4),VI(1,2,3),VI(2,1,3);
MODAut:VI(4,1,2),DVI(1, 2),VI(2,3,4),VI(4,1,2,3),VI(1,2,3,4);
MODWin:RVI(2, 3),VI(2,3,4),RVI(2, 4),VI(2,1,3,4),DVI(2, 3),VI(3,1,2)。
在以上模型的变量中,同时包含B2和B3波段的变量因子出现25次,占比为69%,明显高于IncMSE指标的58%和IncNodePurity指标的57%,表明使用综合指标筛选的结果明显优于单一指标。同时,所有的变量因子都包含了B2或B3波段,再次证明绿光波段B2(0.52~0.59 μm)和红光波段B3(0.63~0.69 μm)是遥感反演叶绿素a浓度的关键波段因子,对准确估算浑浊水体叶绿素a浓度具有重要的意义。
2.3 模型建立
根据上述5个模型筛选的重要特征变量,分别重新构建随机森林模型,其中参数Mtry为特征变量个数的三分之一,分别取1、2、3和4四个数值,Ntree则根据前面误差分析结果分别选取400、500和600三个数值。对应每组参数组合(Mtry,Ntree)重复建模5 000次,从中选出各模型精度最高的参数组合(表2)。由表2可知,在MODAll、MODSpr、MODSum、MODAut和MODWin共5个模型中,秋季模型MODAut精度(R)最高达0.99,对应的参数组合为(2,400),包含全部样本的模型MODAll和冬季模型MODWin精度(R)最小,均为0.84,对应的参数组合分别为(3,400)和(2,600)。

表2 各模型精度Table 2 Each model accuracy
2.4 模型验证
进一步验证模型的反演精度,将上述建立的5个随机森林模型MODAll、MODSpr、MODSum、MODAut和MODWin反演的叶绿素a浓度值,分别与实测叶绿素a浓度值进行比较,各模型叶绿素a浓度估算值和实测值拟合关系见图4。由图可知,各模型估算值与实测值之间均呈现较高的相关性,均方根误差(RMSE)均较低。其中MODAut模型的拟合精度最高,决定系数(R2)为0.96,RMSE为2.1 mg·m-3,MODSum模型次之,R2为0.85,RMSE为2.0 mg·m-3,MODAll模型的拟合精度最低,R2为0.77,RMSE为2.2 mg·m-3。这一结果表明用所有样本构建的模型的拟合效果不如分季节构建的模型,说明分季节模型估算的叶绿素a浓度值更加接近实测值,其中秋季模型拟合效果又明显好于其他3个季节模型。

图4 各模型叶绿素a浓度估算值和实测值之间的散点关系(a)MODAll,(b)MODSpr,(c)MODSum,(d)MODAut,(e)MODWinFig.4 Scatter plots between estimated and measured chlorophyll a concentration of each model(a) MODAll, (b) MODSpr, (c) MODSum, (d) MODAut, (e) MODWin
3 讨 论
有效波段的选择是高精度估算叶绿素a浓度的关键(姜广甲等,2013)。利用随机森林模型识别、量化特征变量重要性的功能,客观筛选出相对重要的变量因子,本文确定了绿光波段(0.52~0.59 μm)和红光波段(0.63~0.69 μm)及其组合为定量反演太湖叶绿素a浓度的关键波段。尽管目前对于浑浊Ⅱ类水体叶绿素a的光谱特征和敏感波段的研究还较少(潘应阳等,2017),但已有一些学者针对不同内陆水体的实测光谱数据进行了分析,得到了类似的结果。有统计表明水体叶绿素a浓度与0.54 μm和0.701 μm反射峰的相关系数接近1,相近波段的特征光谱能较好反演叶绿素a浓度(吴传庆等,2009);水体中藻类最显著的光谱特征是0.56 μm附近的反射峰,该峰值的存在与否通常被认为是判断水体是否含有藻类的依据,而0.682 μm波段与叶绿素a浓度相关性最好(杨婷等,2011);此外,叶绿素a浓度的变化也会影响浮游植物吸收峰的数值和位置,从而影响到最佳波段的选择(潘应阳等,2017)。这些大多是针对特定水体特定区域、选用较少的测量数据的研究结果可能并不具有普适性(冯驰等,2015)。对于较为浑浊的内陆水体,由于存在浮游植物、悬浮物、溶解有机物等许多影响叶绿素a吸收的物质,各组分之间彼此混合、交互作用,水体的光谱特征更加复杂,实际测量的叶绿素a反射吸收峰也会有明显不同(罗建美等,2017)。因此,利用随机森林模型确定叶绿素a光谱特征的关键波段,可以避免特定水域、特定叶绿素a浓度测量的局限性,对于定量遥感反演大面积浑浊Ⅱ类水体叶绿素a浓度不失为一次有益的尝试。
太湖叶绿素a浓度具有明显的时空分布特征(乐成峰等,2008)。本文利用春、夏、秋、冬四个季节的随机森林模型,分析了太湖叶绿素a浓度的时空分布特点。图5为2018年全湖叶绿素a浓度均值随时间的变化情况,可见夏季平均叶绿素a浓度最高,冬季最低,二者平均浓度分别为9.6 mg·m-3和7.1 mg·m-3,秋季由于受到夏季高浓度的影响,叶绿素a浓度高于春季,分别为8.6 mg·m-3和7.7 mg·m-3,这与乐成峰(2008)研究较为一致。以一景影像代表各季节的空间分布情况(图6),可以看到冬季叶绿素a浓度较低,空间变化不明显,这与冬季温度降低有关(贾春燕,2008);春季叶绿素a浓度开始出现较明显的空间变化,西北部湖区,特别是梅梁湖和竺山湖附近叶绿素a浓度较高,向湖心区逐渐减小,这主要是由于存在众多的入湖河流和高密度城市排污口,造成水体富营养化严重(刘聚涛等,2011);而夏、秋季叶绿素a浓度空间变化最为显著,西部沿岸区、竺山湖、梅梁湖和部分湖心区叶绿素a浓度明显偏高,除了与富营养化程度有关外,还与夏、秋季盛行东南风引起的湖流有关(秦伯强等,2004)。东太湖部分水域叶绿素a浓度始终呈现相对较高的水平,则可能是受该区域丰富的水生植物影响。考虑到太湖各区域均存在不同程度的水生植物,且随着季节交替,水生植物面积变化幅度较大(Zhao et al, 2013),因此,本研究参考了相关文献(杨婷等,2011;朱云芳等,2017),没有将水生植物剔除,可能会对叶绿素a浓度反演产生干扰,后续将会进一步研究水生植物的影响。另外,本文仅采用了2018年1月至2019年5月的资料,且由于高分卫星观测条件限制,数据时序不连续,因此需要进一步搜集更多数据,增加样本数,以期构建更为精确的模型。

图5 2018年太湖叶绿素a浓度时间变化Fig.5 Temporal variation of chlorophyll a concentration in Taihu Lake in 2018
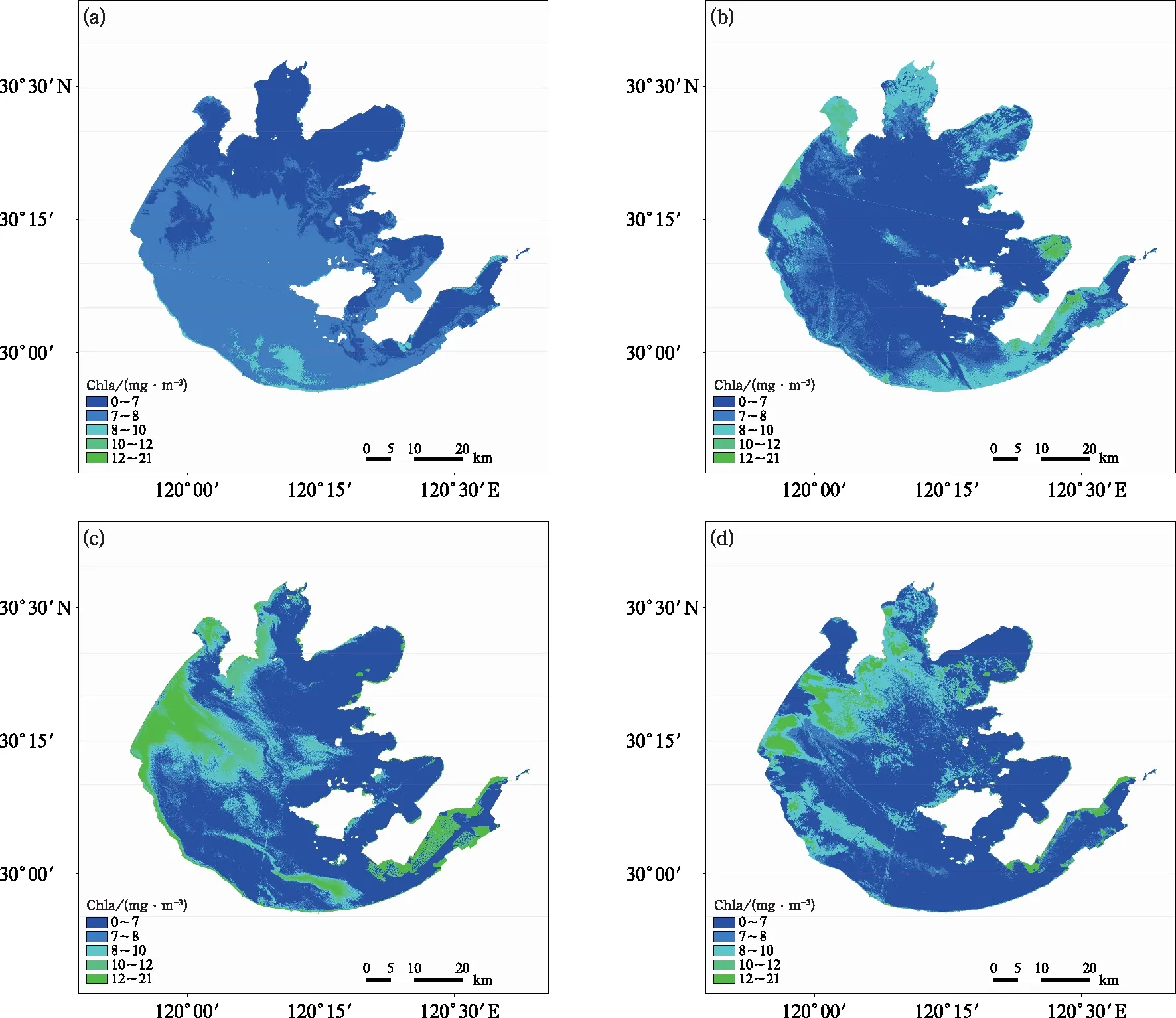
图6 各季节太湖叶绿素a浓度空间分布(a)冬季,(b)春季,(c)夏季,(d)秋季Fig.6 Spatial distribution of chlorophyll-a concentration in Taihu Lake in each seasons(a) winter, (b) spring, (c) summer, (d) autumn
由于人工采样实验室分析法和水质浮标站自动监测法在原理、方法和步骤等方面不同,加之太湖湖体各处的藻种、水质存在较大差异,人工采样实验室分析与自动监测的叶绿素a浓度之间的差异较大。据江苏省环境监测中心利用全湖人工观测数据与原位观测数据对比,表明人工采样分析与自动监测数据之间的相关性较差,整体而言,人工采样分析得到的结果约为自动监测的2.4倍。因此,本文利用自动监测数据来估算的叶绿素a浓度,比目前大多数采用人工采样实验室分析数据的估算结果要明显偏小(曹红业等,2016;冯驰等,2015;宋挺等,2017),但可能更客观地反映了太湖湖体叶绿素a浓度及其分布状况。水质参数的自动监测分析应当是今后的必然趋势,事实上,近年来江苏省太湖水污染防治工作中使用的叶绿素a浓度数据就主要来自于自动监测结果,因此有必要在后续的研究中搞清楚自动观测数据和人工采样数据之间的关系。
4 结 论
(1)用随机森林模型可以确定绿光波段和红光波段为遥感反演太湖叶绿素a浓度的关键波段,但仍需结合其他波段,这样可以避免特定水域、特定叶绿素a浓度测量的局限性,结果更客观。
(2)分季节构建的太湖叶绿素a浓度随机森林估算模型能够得到更加接近实测值的结果,春、夏、秋、冬各季模型的决定系数R2分别为0.84、0.85、0.96和0.82,RMSE分别为1.9、2.0、2.1和1.5 mg·m-3。
(3)太湖叶绿素a浓度呈明显时空变化特征,其中夏季叶绿素a浓度最高,秋、春季次之、冬季最低;春、秋和夏季全湖叶绿素a浓度空间变化较明显,冬季空间变化不明显,叶绿素a浓度高值区主要集中在西部沿岸区、竺山湖、梅梁湖和部分湖心区。
(4)模型使用实测数据来源于水质浮标站自动监测,跟人工采样实验室分析法获得结果相比明显偏低,这是因为两种监测方式在原理、方法和步骤等方面有所不同,而且太湖湖体不同区域的藻种、水质也存在较大差异。但水质自动化监测是未来的发展方向,充分利用好自动观测数据具有重要的现实意义。
